压水堆一回路环境中304不锈钢的蠕变特性分析
薛 河,崔英浩,赵凌燕,唐 伟,倪陈强
0 引言
应力腐蚀开裂(stress corrosion cracking,SCC)是核电一回路安全端异种金属焊接接头在服役过程中的一种重要失效形式[1-3]。在应力腐蚀的过程中,核电结构材料长期在高温高压下工作,同时由于裂尖区域高应力区的存在,使得裂尖附近会产生蠕变现象[4-5]。裂尖附近的蠕变与腐蚀性介质、力学性能不均匀性以及环境因素一起诱导裂尖产生应力腐蚀开裂行为,其对SCC应力腐蚀裂纹扩展速率会产生很大的影响[6-7]。
由于核电一回路的水环境温度为288~340℃[8],核电焊接接头区域在实际工况下中发生的蠕变属于“低温”(蠕变温度在0.3Tm以下,Tm为材料的熔点)蠕变,而裂尖存在高应力区,因而更易于发生“低温”高应力下的蠕变现象[9-10]。实际上,在高温高压水环境下600合金等材料的蠕变已为试验所证实[11]。因此研究核电结构材料在“低温”高应力条件下的蠕变现象已显得尤为重要。国外的一些学者也提出裂尖蠕变导致环境致裂的设想,国外学者Gary S.Was对合金600退火处理后进行了337℃和360℃下的“低温”下的蠕变试验,提出了蠕变率可以表示为应力的函数,并得到了不同“低温”和应力下的蠕变量和蠕变速率[12]。I.A.Shibli对360℃下C-Mn合金的蠕变裂纹扩展特征进行了定量表征,并估计了与裂纹扩展速率最密切的参数C*的大小(描述蠕变区域比较大时的合适断裂参量)[13]。张乐福研究了超临界水环境下30%冷加工不锈钢的蠕变对SCC裂纹扩展速率的影响,结果表明冷加工690钢承受了对穿晶开裂更高的敏感性,同时蠕变对SCC开裂的贡献达到了90%以上[14]。Rui Wu等利用CT试样研究了反应堆压力容器用低合金钢A508在320~420℃之间的蠕变裂纹扩展情况[15]。
为了解核电焊接接头基体金属304不锈钢在核电水环境中的蠕变规律,本文在高压釜环境中对其进行了不同应力下的单轴拉伸蠕变实验,并利用最小二乘法原理对实验数据进行了拟合处理,得出了该304不锈钢在320℃下的蠕变本构方程,并利用有限元软件ABAQUS建立了高应力下蠕变数值模拟的方法。
1 试验方法
1.1 试样及其力学性能
使用试样为车间批次生产的304不锈钢,熔点为1390℃,并进行30 min的固溶处理,其化学成分见表1,按照 GB/T 2039 -1997 标准[16],通过卷板机将板材轧制成2 mm厚的钢板,在剪板机上裁剪成400 mm×400 mm,随后利用线切割机对其进行慢走丝线切割,最后打磨毛刺,加工后试样的几何形状和尺寸如图1所示,其厚度为2 mm,标距段长度20 mm,宽度3 mm,销孔直径8 mm,总长度74 mm.利用YYF-30慢应变速率应力腐蚀试验机得出的304在320℃下的工程应力应变曲线,并通过工程应力应变与真实应力应变之间的转化关系推导出真实应力应变力学性能曲线如图2所示,该温度下的力学性能参数见表2.

表1 304不锈钢的化学成分Tab.1 Chemical composition of 304 stainless steel(%)

表2 304不锈钢在320℃下的拉伸性能Tab.2 Mechanical property of 304 stainless steel at 320 ℃

图1 矩形蠕变试样的示意图Fig.1 Sketch of rectangular creep specimen(mm)

图2 拉伸过程中的真应力-真应变曲线Fig.2 Curve of true stress-true strain in loading
1.2 试验条件
按照GB/T 2039-1997《金属拉伸蠕变及持久实验方法》[16],利用矩形标准蠕变试样,利用YYF-30慢应变速率应力腐蚀试验机进行恒载荷蠕变试验,如图3所示,该试验机具有温度压力采集系统、釜内压力检测系统和双位移传感器测量系统等,可以保证釜内的压力保持在15 MPa,依据核电一回路的环境温度,确定高压釜的工作温度为320℃,施加的载荷恒定且为400,450和500 MPa,拉伸起始阶段采用0.5 mm/min的恒应变速率,在达到设置的载荷标准值时自动调整为恒载荷控制,实验过程中利用2个位移传感器自动记录的位移平均值作为实际位移值,釜内为超纯水环境,温度通过热电偶进行准确测量,釜内压力由背压阀提供,数据显示在面板上,实验过程实时记录数据,每分钟记录1个数据。同时为了保证高温拉伸实验与单轴蠕变实验数据的可靠性,所用试样均为同一批次,本文的蠕变试验条件见表3.

表3 蠕变拉伸的试验条件Tab.3 Experiment conditions of creep stretching

图3 YYF-30慢应变速率应力腐蚀试验机Fig.3 YYF -30 slow strain stress corrosion testing machine
2 实验结果与分析
2.1 材料的蠕变实验曲线
图4为304不锈钢在320℃下400,450,500 MPa应力下蠕变500 h之后的蠕变曲线,从图4可以看出,304不锈钢在长时间恒载荷作用下,出现了典型的“低温”下的蠕变现象,且所有的蠕变曲线都呈现出加速蠕变阶段和稳态蠕变阶段,随着应力水平的增大,蠕变变形也更为明显。蠕变时间为500 h下,应力分别为400,450,500 MPa时对应的蠕变变形量分别为:0.121,0.146 和 0.174.在蠕变刚开始时,即初期蠕变速率特别大,随后随着时间的增加蠕变速率逐渐减小,随后呈现平稳特征,蠕变时间越长,蠕变变形越明显,这种现象的出现主要是由于温度较高时,原子的活动能力提高,使得产生塑性变形的位错滑移更加容易,在该过程中加工硬化也随之产生[17],从而导致稳态蠕变阶段的蠕变速率明显低于加速蠕变阶段的速率;从表4可以看出,不同应力下的稳态蠕变速率也不一样,应力分别为400,450,500 MPa时对应的稳态蠕变速率分别为:7.6 ×10-8s-1,11.1 ×10-8s-1和 13.1 ×10-8s-1,即随着应力的增大,稳态蠕变速率也越大。通常认为在试验温度低于0.4Tm时,蠕变变形机制主要是位错滑移导致的[18-19],因此可以认为该温度下304不锈钢的蠕变也是位错滑移产生的。

表4 304不锈钢的蠕变速率Tab.4 Creep rate of 304 stainless steel
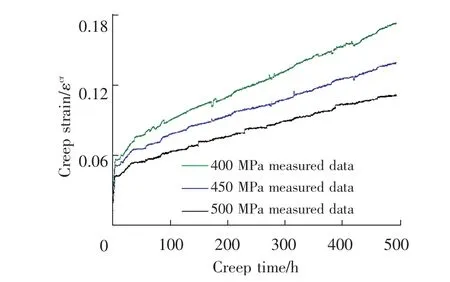
图4 304不锈钢的蠕变曲线(320℃,400~500 MPa)Fig.4 Creep curve of 304 stainless steel(320 ℃,400 ~500 MPa)
2.2 蠕变本构方程的建立
对金属材料而言,蠕变曲线前2个阶段具有几何形式上类似的性质,因此蠕变应变可以写成应力、时间和温度函数的乘积[20-21],可用式(1)表示

该蠕变模型材料参数较少,结构形式相对简单,而且可以准确地描述蠕变的变化,因此在工程上有广泛的应用。
式(1)中蠕变变形随应力变化的变化规律采用 Norton 公式[22-23]

式(2)蠕变变形的时间变化规律采用Andrade提出来的经验公式[24]

蠕变变形随温度的变化规律

式中 各材料参数均为材料常数;R为玻耳兹曼常数;ΔH材料的表面激活能。
因文中的蠕变试验是在恒定的温度下进行的,因此公式(1)可以简化为公式(5),其中A'为包括温度在内的所有常数的乘积,即幂律模型中的时间硬化模型对蠕变曲线进行拟合,来求得相应的蠕变参数

利用最小二乘法对所得的蠕变曲线进行拟合,得到320℃下304不锈钢材料的蠕变参数见表5.

表5 304SS时间硬化模型的拟合材料参数的结果Tab.5 Creep parameters of 304SS by power law
图5为根据拟合的结果所得到的实验与拟合曲线的对比图,从图5可以看出,得到的本构模型可以很好的反映了304不锈钢在320°下的蠕变行为。
因此可以得出304SS的蠕变幂模型为

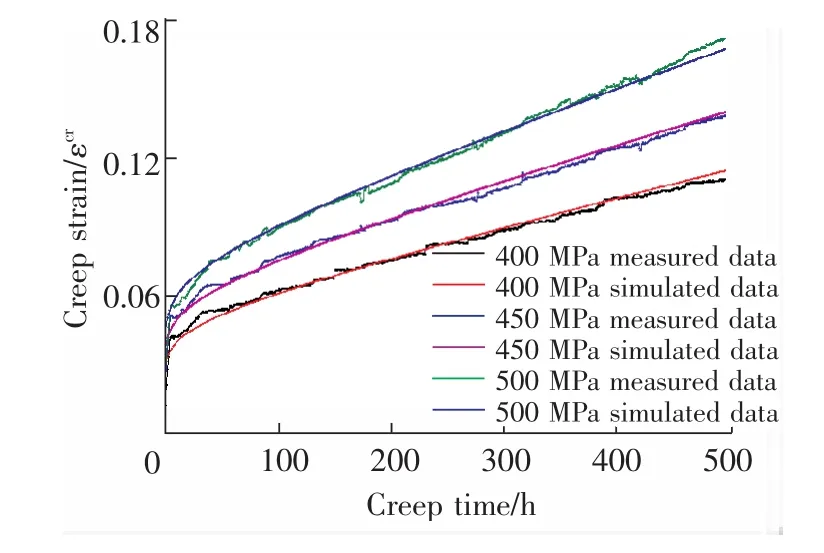
图5 试验蠕变曲线与拟合蠕变曲线的对比Fig.5 Comparison between fitted creep curve and experimental results
3 高应力下蠕变数值模拟方法的建立
利用 ABAQUS[25-27]软件建立了含椭圆形缺口的304不锈钢单轴蠕变试样的有限元模型,为满足最大应力不超过材料的抗拉强度,通过有限元计算,设置椭圆形缺口的长半轴和短半轴分别为0.1和0.2 mm,如图6所示,有限元网格类型为C3D8,单元数为7 662,为了得到缺口处高应力区域的蠕变规律,在缺口处进行了网格细化,最小网格尺寸为5μm.
在进行有限元分析的过程中,材料塑性模型为在高压釜内测得的真实应力应变曲线,蠕变的当量时间同样设置500 h,边界条件采用试样左端圆孔完全固定,在右边圆孔中心建立参考点,并与右端圆孔后半部分进行耦合,在参考点处施加与试验一致的集中载荷。

图6 单轴拉伸试样的蠕变的有限元模型Fig.6 Finite model of axial creep specimen
由于ABAQUS中对蠕变本构关系中时间硬化模型的公式如式(7)所示

对式(6)进行求导得出蠕变应变率公式如式(8)所示,通过对照式(7),得出ABAQUS模拟需要的蠕变参数,分别是幂率常数A为9.8×10-10,等效偏应力指数2.56,时间常数m为-0.64.

为了得到高应力下的304不锈钢的蠕变规律,选取近缺口处的3个位置,应力分别为750,800,850 MPa,得到该3个应力下蠕变500 h的蠕变变化规律,如图7所示。
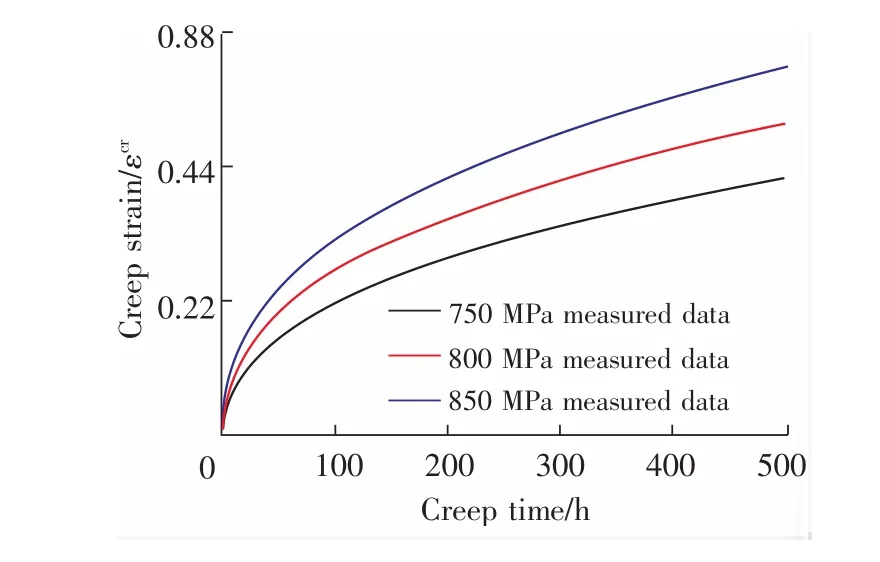
图7 数值模拟出高应力下的蠕变曲线Fig.7 High stress creep curve of numerical simulation
图7 为通过数值模拟得到的304不锈钢在320℃下750,800,850 MPa应力下的蠕变曲线,其与利用蠕变幂模型外推出来的高应力下的蠕变曲线规律一致,可以得出,通过蠕变幂率本构模型可以准确得出高应力下的的蠕变曲线,为后续研究核电材料“低温”高应力蠕变提供了一种依据。
4 结论
通过对304不锈钢进行了320℃时不同应力下的蠕变试验,得出主要结论如下
1)基于蠕变应变和蠕变时间之间的关系,建立了基于时间硬化模型的蠕变本构关系;
2)应力和时间对蠕变变形有着很大的影响,当温度一定时,应力增大,蠕变变形和蠕变速率随之增大,同时随着时间的增加,蠕变变形也在增大;
3)利用ABAQUS软件建立了高应力下蠕变数值模拟方法,得出了高应力304不锈钢的蠕变曲线,验证了数值模拟方法的可行性,同时为后续研究核电材料裂尖区域“低温”高应力蠕变提供了一种依据。
[1] 马 成,彭群家,韩恩厚.核电结构材料应力腐蚀开裂的研究现状与进展[J].中国腐蚀与防护学报,2014,34(1):37 -45.MA Cheng,PENG Qun-jia,HAN En-hou.Review of stress corrosion cracking of structural materials in nuclear power plants[J].Journal of Chinese Society for Corrosion and Protection,2014,34(1):37 -45.
[2] Andresen P L,Karen G,Lawrence N J.Stress corrosion cracking of sensitized type 304 stainless steel in 288C water:A five laboratory round robin[M].Indianapdis:John Wiley and Sons,Inc.2013.
[3] Xue H,Sato Y,Shoji T.Quantitative estimation of the growth of environmentally assisted cracks at flaws in light water reactor components[J].Journal of Pressure Vessel Technology,2009,131(1):41 -49.
[4] Scully J C.Stress corrosion crack propagation:a constant charge criterion[J].Corrosion Science,1975,15(4):207-224.
[5] Huang X,Zhang Y,Mei M,et al.A quantitative prediction model of SCCrate for nuclear structure materials in high temperature water based on crack tip creep strain rate[J].Nuclear Engineering and Design,2014,278(8):686-692.
[6] 卢建树,王保峰,张九渊.高温水中不锈钢和镍基合金应力腐蚀破裂研究进展[J].核动力工程,2001,22(3):259-263.LU Jian-shu,WANG Bao-feng,ZHANG Jiu-yuan.A review of stress corrosion cracking studies of stainless steels and nickel base alloys in high temperature water[J].Nuclear Power Engineering,2001,22(3):259-263.
[7] Yi Y,Was G S.Stress and temperature dependence of creep in Alloy 600 in primary water[J].Metallurgical&Materials Transactions A,2001,32(10):2553 -2560.
[8] He X,Shoji T.Quantitative prediction of EAC crack growth rate of sensitized type 304 stainless steel in Boiling water reactor environments based on EPFEM[J].Journal of Pressure Vessel Technology,2007,129(3):460-467.
[9] 崔英浩,薛 河,赵凌燕,等.蠕变性能失配对应力腐蚀裂尖力学场的影响[J].热加工工艺,2017(12):81-85.CUI Ying-hao,XUE He,ZHAO Lin-yan,et al.Effect of creep property mismatch on mechanical field at crack tip[J].Hot Working Technology,2017(12):81 - 85.
[10] Kassner M E,Smith K.Low temperature creep plasticity[J].Journal of Materials Research and Technology,2014,3(3):280 -288.
[11] Yi Y,Was G S.Stress and temperature dependence of creep in Alloy 600 in primary water[J].Metallurgical and Materials Transactions A,2001,32(10):2553-2560.
[12] Jr M M H.Interacting sensitivities of alloy 600 PWSCC to stress intensity factor,yield stress,temperature,carbon concentration,and crack growth orientation Alloy 600[J].Corrosion Science,2017,125(15):152 -165.
[13] Shibli I A.Low temperature(360 C)creep crack growth characteristics of a C - Mn steel[J].Materials Science and Engineering A,1988,104:29 -35.
[14] Zhang L,Chen K,Du D,et al.Characterizing the effect of creep on stress corrosion cracking of cold worked Alloy 690 in supercritical water environment[J].Journal of Nuclear Materials,2017,492(15):32 -40.
[15] Wu R,Sandstr m R,Seitisleam F.Low temperature creep crack growth in low alloy reactor pressure vessel steel[J].Journal of Nuclear Materials,2005,336(336):279-290.
[16] 李久林,梁新邦.GB/T2039—1997金属拉伸蠕变及持久试验方法国家标准编制说明[J].冶金标准化与质量,1998(3):4-8.LI Jiu-lin,LIANG Xin-bang.GB/T2039—1997 Test method for tensile creep of metals and sustainable standards presentation[J].Metallur Gical Standardization and Quality,1998(3):4 -8.
[17] 张俊善.材料的高温变形与断裂[M].北京:科学出版社,2007.ZHANG Jun-shan.Material of high temperature deformation and fracture[M].Beijing:Science Press,2007.
[18]余 珂.高温焊接结构稳态蠕变变形速率的研究[D].南昌:南昌大学,2007.YU Ke.Study on the steady-state creep deformation rate for high-temperature weld structures[D].Nanchang:Nanchang University,2007.
[19] Frost H J,Ashby M F.Deformation-mechanism maps:the plasticity and creep of metals and ceramics[M].U-nited Kingdom:Pergamon Press,1982.
[20] 韩宁宁,顾剑锋.核电用Inconel 600合金的蠕变行为[J].金属热处理,2016,41(6):1 -3.HAN Ning-ning,GU Jian-feng.Creep behavior of Inconel 600 alloy used for nuclear power[J].Heat Treatment of Metals,2016,41(6):1 -3.
[21] 马 越,彭赫力,陈 源,等.500℃下TB2钛合金蠕变本构方程[J].塑性工程学报,2016,23(5):139-143.MA Yue,PENG He-li,CHEN Yuan,et al.Creep constitutive equation for TB2 titanium alloy at 500 ℃[J].Journal of Plasticity Engineering,2016,23(5):139-143.
[22] 朱 智,张立文,顾森东.Hastelloy C-276合金应力松弛实验及蠕变本构方程[J].中国有色金属学报,2012,22(4):1063 -1067.ZHU Zhi,ZHANG Li-wen,GU Sen-dong.Stress relaxation test of Hastelloy C-276 alloy and its creep constitutive equation[J].The Chinese Journal of Nonferrous Metals,2012,22(4):1063 -1067.
[23] 徐连勇,荆洪阳,安俊超,等.P92钢焊接接头蠕变本构关系[J].焊接学报,2009,30(12):29 -32.XU Lian-yong,JING Hong-yang,AN Jun-chao,et al.Creep constitutive equations of P92 steel welded joint[J].Transactions of the China Welding Institution,2009,30(12):29-32.
[24] Sawada K,Tabuchi M,Kimura K.Analysis of long-term creep curves by constitutive equations[J].Materials Science and Engineering A,2009,510(10):190 -194.
[25] 庄 茁.ABAQUS/Standard有限元软件入门指南[M].北京:清华大学出版社,1998.ZHUANG Zhuo.Introduction guide to finite element software of ABAQUS/Standard[M].Beijing:Tsinghua University Press,1998.
[26] 付凯敏,黄晓明.基于ABAQUS的修正Burgers蠕变模型二次开发[J].公路工程,2008,33(3):132-137.FU Kai-min,HUANG Xiao-ming.The secondary development of modified burgers creep model Based on ABAQUS general software[J].Highway Engineering,2008,33(3):132 -137.
[27] 阎 岩,王思敬,王恩志.基于西原模型的变参数蠕变方程[J].岩土力学,2010,31(10):3025 -3035.YAN Yan,WANG Si-jing,WANG En-zhi.Creep equation of variable parameters based on Nishihara model[J].Rock and Soil Mechanics,2010,31(10):3025-3035.

