基于传递系数方法的贯流转桨式水轮机的仿真模型

,

(广西大学电气工程学院，广西 南宁 530004)

1 引言

贯流式水轮机是近几年新发展起来的一类水轮机，是一种低水头、大流量、高比速的水轮机[1]。贯流式水轮机由于基本没有设置水流转弯的流道，从流道进口到尾水管出口，水流几乎呈直线流动的形式，水流动能的损失很小，水力的效率很高。贯流式水轮机的流道形式和轴流式水轮机不同，但是对于贯流式水轮机而言其结构上与轴流式水轮机依然有很多相似的地方，例如，贯流式水轮机的转轮与轴流式水轮机的相同，因此从水力机械的角度来看，其装置的过渡过程与轴流式水轮机有许多相近之处[1]。

贯流式水轮机在国内外的发展与应用非常迅速，国外25米水头以下的水头开发，贯流式水轮机已经基本上取代了轴流式水轮机。贯流式机组在1960年代至1990年代发展最为迅猛，这一时期投入运行的贯流机组，最大单机容量达到了65.8Mw(灯泡贯流，日本只见)，最大水轮机直径8.2米(竖井贯流，美国墨累)，最高工作水头达到22.45米(灯泡贯流，日本新乡第二)[2]。

国内从1960年代开始研究贯流式水轮机，1983年湖南马迹塘水电站和1984年广东白垢电站的建成标志着国内具有研制大容量的贯流式水轮机的能力。在最近的几十年里，国内的贯流式水轮机的技术水平得到了长足的发展，通过引进设备，合作生产和自行研发，国内建成了安装有大型贯流式水轮机的水电站数十座，如王甫洲、长洲、洪江等。

贯流式机组的结构特征决定了他的过渡过程具有许多不同于常规机组的特点：

(1)相比于其他类型的水轮机，贯流式水轮机机组飞轮力矩偏小，转子的惯性常数值仅为1～2s，水体附加惯性所占比重大，相比于立式发电机组的惯性系数7～10s，导致了其甩负荷时升速极快，甩负荷过程极短。

(2)由于水头低、流量大，贯流式水轮机装置中的引水系统具有相当大的水流惯性常数，这也导致了水击效应中的压力相对值也很大，且在上游也容易引起浪涌。如果甩负荷时导叶关闭过快，尾水管进口的水压降低的值将很大，甚至可能引起断流反水击效应。

(3)水轮机的转轮前面压力较立轴式的要小，转轮后部压力差别很小。

由于以上的这些特点，贯流式水轮机的机组动态附加载荷很大，其甩负荷过渡过程的控制十分重要。

对于现有的电力系统的相关研究而言，在不同类型水轮机的研究深度上面是很不平衡的，对于传统类型的一些水轮机研究的比较深入。例如，对混流式水轮机的研究最为全面，由于使用的时间很长，因此其特性曲线比较完整，对不同直径和功率的机组的传递系数有着很全面的了解。相比较而言，对于轴流式水轮机的研究要比混流式水轮机的研究要晚上许多，但是随着轴流式水轮机的使用，对于电力系统而言，轴流式水轮机的仿真模型也有了深入研究，例如文献[3]中对轴流转浆式水轮机的仿真模型的建立就有了比较深入的介绍。但是对于贯流式水轮机而言，却一直缺少介绍贯流式水轮机仿真模型的相关论文，本文力图从贯流式水轮机的仿真模型的建立来入手，介绍一种利用传递系数来建立仿真模型的方法，建立一种可以用于水轮机小波动仿真的模型，对双控制型的水轮机模型采用导叶和桨叶协联控制。然后与二阶发电机模型构成一个完整的原动机-发电机系统，利用多指标非线性控制方法，形成一个协调控制的控制律。进行三相短路扰动的仿真比较这种非线性控制方法和PID控制方法，来验证水轮机模型的正确性。

2 贯流转桨式水轮机的数学模型

虽然现代流体力学的发展使得研究水力机械时，已经可以利用相关的解析方法来描述水轮机的运动形式，但是对于水轮机而言目前仍然主要依靠模型试验方法来定量描述水轮机的工作特性[2]。同时，应当指出的是这些特性曲线描述的是水轮机的稳态工况，当水轮机的角速度变化量较小时，一般取其为额定值，这时其标幺值为1。理论计算的误差与实测结果差别不大，说明在分析时采用这类简化是可以接受的。

2.1 水轮机的状态方程

根据文献[4]中的相关章节对水轮机状态方程的分析，有

一般来讲，水轮机的动态特征用下面的两个方程来表示：

转矩特性：

Mt=Mt(α,n,φ,H)

(1)

流量特性：

Qt=Qt(α,n,φ,H)

(2)

在上面两式中，α表示导叶开度角，n表示水轮机转速，φ表示桨叶开度角，H表示水头。上面的状态方程可以作为水轮机状态方程的一般式来使用。

那么首先假设在小波动情况下，设水轮机的初始工况点α=α0,n=n0,φ=φ0,H=H0；当进入到动态过程中时，有α=α0+Δα,n=n0+Δn,φ=φ0+Δφ,H=H0+ΔH；利用泰勒级数在初始状态点进行展开。

mt=eyy+exx+ezz+ehh

(3)

q=eqyy+eqxx+eqzz+eqhh

(4)

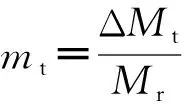
上面的式(3)、(4)中的各项系数，都可以通过特征曲线上的切线斜率来求出，其中，ey表示转矩对导叶开度的传递系数，ex表示转矩对转速的传递系数，ez表示转矩对桨叶开度的传递系数，eh表示转矩对水头的传递系数，eqy表示流量对导叶开度的传递系数，eqx表示流量对转速的传递系数，eqz表示流量对桨叶开度的传递系数，eqh表示流量对水头的传递系数。

2.2 引水系统的传递函数

对于导水系统中的刚性水击方程和弹性水击方程的选择问题，在文献[1]中的论述中可以发现，在中、低水头的水力装置上完全可以采用刚性水击方程。

根据文献[1]，对于低水头的水轮机引水系统有传递函数：

(5)

2.3 引水系统与水轮机的模型

利用文献[4]中的方法，结合式(5)可以得到一个完整的引水与水轮机的模型，其传递函数的框图结构如图1所示。

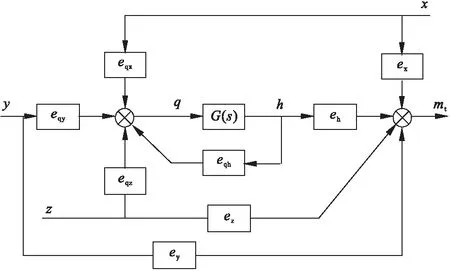
图1 贯流转桨式水轮机传递函数框图

比较文献[3]中的传递函数结构框图可以发现，其结构与轴流转浆式水轮机的基本相同，差别的地方主要体现在参数方面，所以这也与文献[1]中对贯流式水轮机的特点的描述相互印证，表明在数学推导上的正确性。

根据图1中的传递函数框图，可以得到水轮机转矩的一个传递函数：

exx+eyy+ezz]

(6)

将式(5)代入到式(6)，然后求导则得到：

exx+eyy+ezz-mt]

(7)

对于发电机部分，结合参考文献[3]中的方法，可以得到：

(8)

3 水轮机调速器的结构

在工程实践上，最常见和得到最广泛应用的依然是基于PID控制的水轮机调速器，以国内的SJ-721A型微机调速器为例，对于这类调速器而言，可以发现双控型的调速器一般采用导叶开度和桨叶角度同时调节的控制方法，桨叶角跟随导叶开度变化，一般来说，对于双控型水轮机的调速器而言，多数都采用桨叶协联控制的方法。

3.1 桨叶协联调节器

对于采用桨叶协联调节方式的水力发电系统，其各分系统之间的结构如图2所示。

图2 导叶和桨叶协联控制方法下，水力发电系统结构示意图

3.2 接力器的传递函数关系

根据文献[4]和文献[5]可以得到桨叶协联调节器的数学模型和导叶接力器的数学模型，其传递函数分别为：

(9)

(10)

其中(9)为导叶调节器的传递函数，(10)为桨叶接力器的传递函数。

4 发电机与电力系统部分模型

对于发电机和电力系统部分的模型采用二阶的非线性模型[6-7]:

(11)

(12)

5 控制系统数学模型

通过对上面的几个部分的分析的综合，可以得到贯流转桨式水轮机控制系统的数学模型：

(13)

式中,δ、ω、Pm、y和z是控制系统中的五个状态变量，依次表示发电机功角、角速度、机械功率、导叶接力器相对行程和桨叶相对行程。Pe为电磁功率。uy为导叶开度控制信号。TJ、Tw则分别表示转子惯性时间常数和水流惯性时间常数。

通过文献[3,8-9]中所提到的方法可以得到相应的一个非线性控制律。

6 仿真结果

本文中的贯流转桨式水轮机选定了GZ990型；其中的参数根据相应水轮机的特征曲线依次为：

初始状态参数：Per=1,yr=0.79,ωr=1参数均为标幺值。

对仿真模型进行三相短路扰动的MATLAB仿真，对比多指标非线性协调控制方法和传统PID控制面对扰动的稳定性。对两种控制方法在扰动中的频率变化Δω，功率变化ΔPe和功角变化Δδ进行对比，其仿真图如图3(a)～(c)所示：其中黑色虚线表示多指标非线性控制方法下的波形，粉色实线表示的是PID控制方法下的波形；图3(a)～(c)表示的依次为频率变化Δω，功率变化ΔPe和功角变化Δδ。

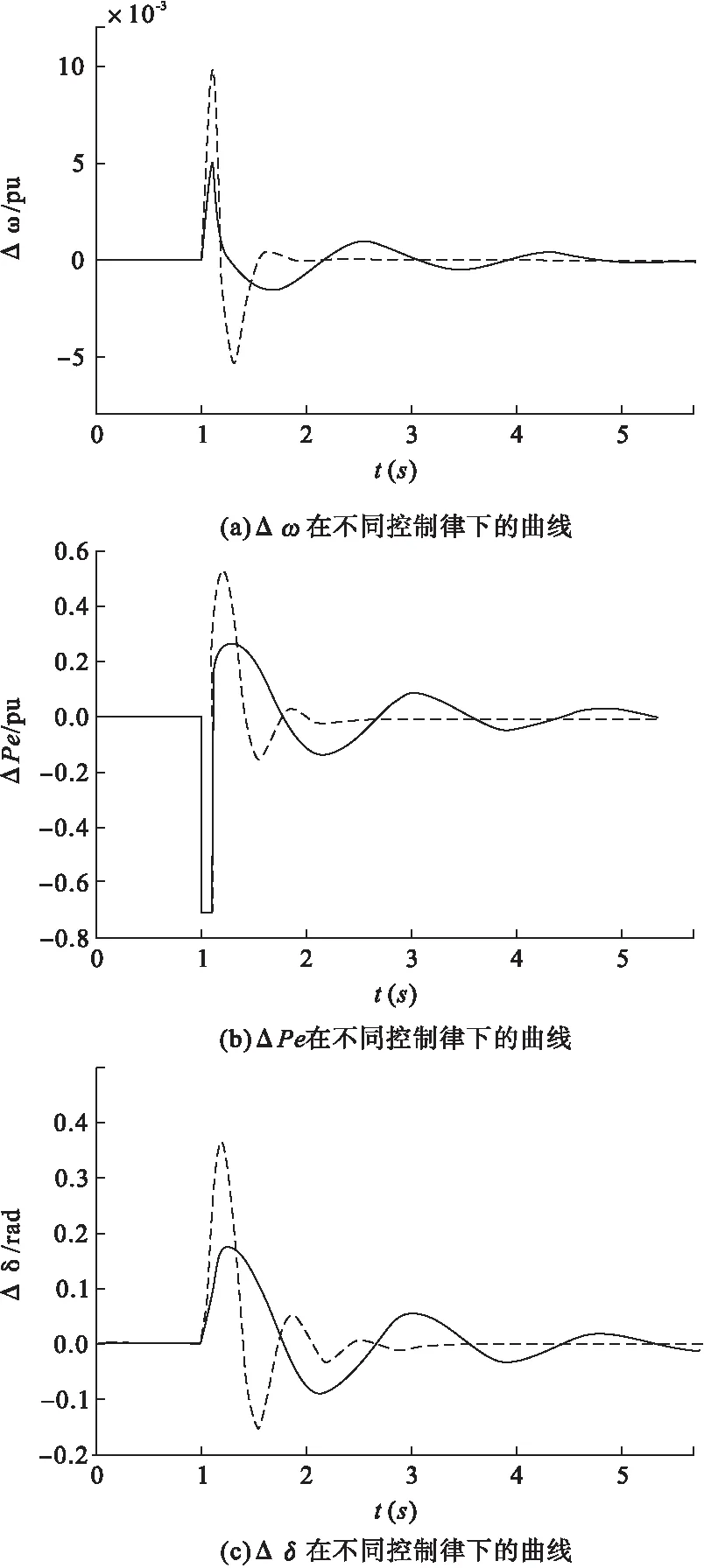
图3 三相短路扰动仿真图像

在1s时，发生三相短路事故，在0.1s后故障被切除，重合闸装置动作，发电机组重新投入系统工作。通过图3可以发现：非线性控制方法使发电系统恢复稳定状态的能力要强于传统PID控制。采用了非线性控制后，在相同的仿真模型下，恢复稳定运行状态的速度更快。从图3(a)中可以发现频率变化Δω采用非线性控制方法后在2s后就基本稳定，而采用PID控制方法在5s后仍然有波动存在。图3(b)中对于功率变化ΔPe而言，采用非线性控制后，其波形在2s后基本稳定，而PID控制则在5s后仍有波动。图3(c)里可以发现功角变化Δδ采用非线性控制时，在3s后系统恢复稳定，而采用PID控制则至少5s后才能恢复稳定。

7 结论

从上面的仿真实验结果来看，一方面说明了这种非线性控制的优点；另一方面则说明，采用传统的传递系数方法，如果可以得到相应型号贯流转桨式水轮机的特征曲线的话，那么依然可以使用这种方法来构建适合的模型用在小波动情况下的水力发电系统仿真，验证了这种建模方法完全可以用在贯流转桨式水轮机上。