H型垂直轴风力机气动参数对主轴偏振效应的影响

张立军，米玉霞，赵昕辉，马东辰，马文龙，王旱祥，刘静



H型垂直轴风力机气动参数对主轴偏振效应的影响

张立军，米玉霞，赵昕辉，马东辰，马文龙，王旱祥，刘静

(中国石油大学(华东) 机电工程学院，山东 青岛，266580)

针对1种1.5 MW H型对称翼垂直轴风力机(VAWT)，采用双致动盘多流管理论，分析主轴偏振效应的产生机理，提出采用变差系数来衡量主轴合成力的振荡程度，并对不同风力机参数对偏振效应的影响进行分析。研究结果表明：风力机叶片在旋转1周范围内产生的气动力合成到主轴位置上后不能互相抵消，发生振荡且作用方向不定；对于大型垂直轴风力机，风剪效应的存在有利于降低主轴偏振效应；在H型垂直轴风力机气动设计中，当叶片数为3片时，主轴振动幅度最小；当高径比为0.508 8时，主轴振动幅度最小；当展弦比为14.201 5时，主轴振动幅度最小。

垂直轴风力机(VAWT)；偏振效应；风剪效应；展弦比

风能作为一种可再生能源，具有储量大、清洁无污染、地域分布广等诸多优点。从技术角度上讲，地球上可以利用的风资源比水资源更丰富，约为200 亿kW，发电量达到13 PW∙h[1−3]，能够很好地满足全球的电力需求。然而，当前风电机组的使用寿命较短，从技术商业化程度来看，难以保证风电机组使用寿命达到20 a，因而，对所有部件的可靠性都需要进行深入的研究[4−5]。伴随世界能源需求持续增长，大量的陆地风电场和海上风电场投入使用，风力发电机组的风轮直径不断增大，安装高度不断增加，受到风剪切、塔影、湍流等因素的影响程度不断增加，在运行过程中产生的不平衡受力荷载随之增大[6−7]，这使风力机产生振动及疲劳损坏。而主轴系统作为 H 型垂直轴风电机组连接风轮和增速齿轮箱的重要组成部分，不仅承受着风轮巨大的重力作用，而且受到其传递的复杂的气动载荷作用，因此，主轴系统在极限工况下有较大的安全裕度，这关系到整个风电机组能否安全工 作[8]。对于风力机主轴系统，国内外学者对主轴结构进行了较多研究，如：MATTHEW等[9]对风电机组主轴轴承进行了理论寿命分析，在分析中考虑了工作温度对轴承寿命的影响，为轴承的结构设计与选型提供了参考；SOUICH等[10]对风电机组主轴轴承座强度进行了分析，为轴承座的结构设计提供了帮助；韩德 海[11]对某2点支撑的主轴系统进行分析时，应用MSC软件，采用刚性面模拟调心滚子轴承，为主轴结构高效分析提供了一种可行的方法；霍玉玲[12]使用 MPC (多点约束)模拟调心滚子轴承，对风力机主轴静强度进行了分析，给出了一种模拟调心滚子轴承的方法；史文博[8]根据Hertz接触及弹性流体润滑理论，对主轴回转支承轴承在润滑状态下的综合径向刚度进行了理论计算，分析了主轴系统中轴承忽略油膜刚度的合理性，为主轴系统准确分析提供了参考[8]。张婷婷等[13−14]根据多岛遗传算法并结合 Isight软件对大功率垂直轴风电机组主轴结构进行了优化设计，为主轴减重提供了参考。从以上分析来看，国内外学者大多是从风力机主轴结构或主轴安装角度进行研究，为延长主轴及相关部件的寿命提出了许多方法。但这些研究过程较少涉及风力机工作时风载荷对主轴产生的影响，尤其是对主轴偏振效应的研究更少。为此，本文作者分析风力机在工作过程中主轴受力过程，得出垂直轴风力机主轴偏振效应的产生机理，并提出衡量主轴合成力振荡程度的变差系数。在此基础上，研究风剪效应、叶片数、高径比和展弦比对主轴振动幅度的影响规律，以便为进一步设计高可靠性的垂直轴风力机结构提供理论参考。

1 偏振效应产生机理分析

1.1 模型建立

采用双致动盘多流管模型[15−16]对叶片进行载荷分析，如图1所示，假设一系列相同的流管通过转子，应用动量方程，每个流管作用在叶片翼型上的流向力相等，且风力机的转子根据上、下风区分为2个致动盘，即第1个致动盘表示上风区中的半个转子扫掠面，第2个致动盘表示下风区中的半个转子扫掠面。本文采用的流管数为30个。

对于垂直轴风轮，通过矢量图解法得到1个叶片分别在上风区和下风区的受力情况，如图2所示。图1和图2中：u和a分别代表垂直轴风轮上、下风区的诱导速度，两者均小于来流风速v；e为2个致动盘之间的均衡诱导速度；w为流过风力机的尾迹速度；为风轮的旋转角速度，为切向风速；为诱导速度和切向速度的合成风速；为叶片攻角，是合成风速方向与叶片弦长方向的夹角；为叶片方位角，当方位角位于0°~180°时，该区域称为风轮的上风区；当位于180°~360°时，该区域称为风轮的下风区。

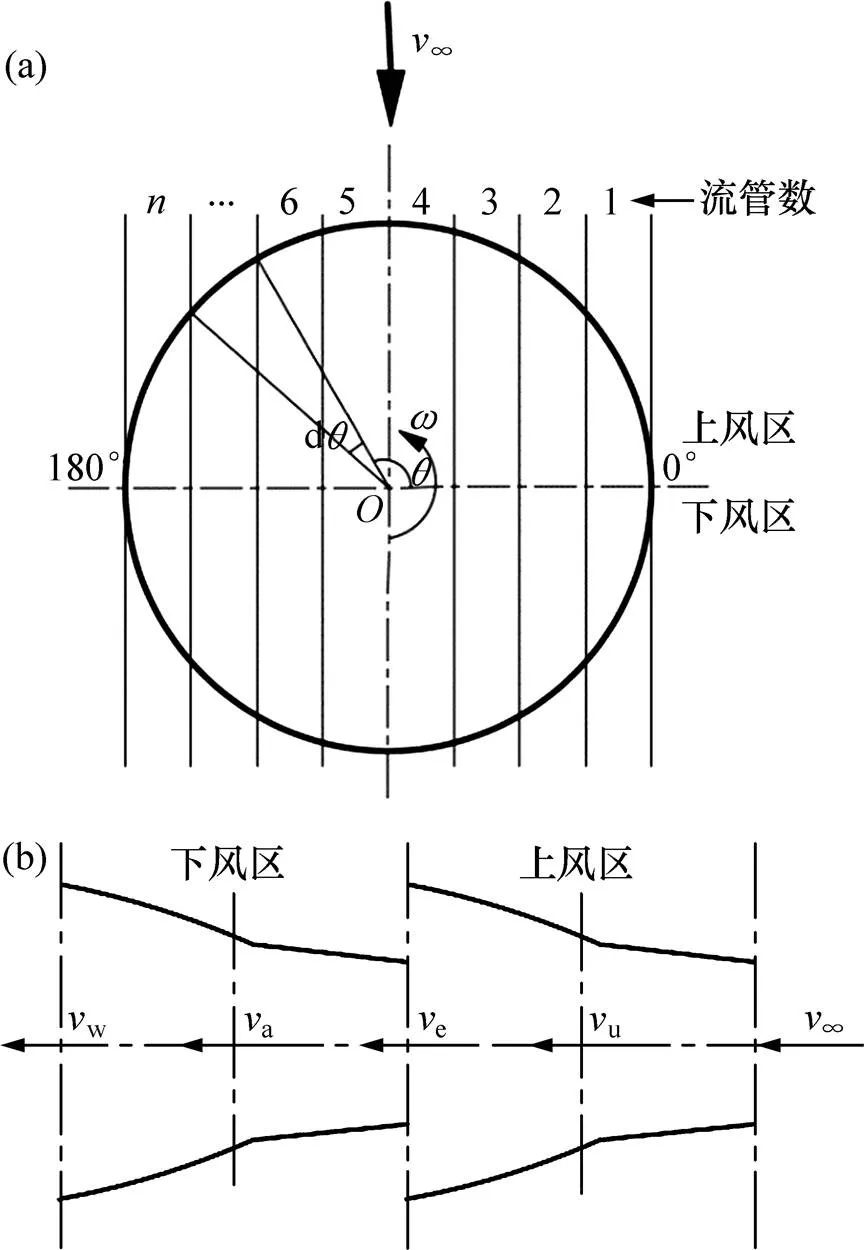
(a) 模型俯视图；(b) 模型主视图

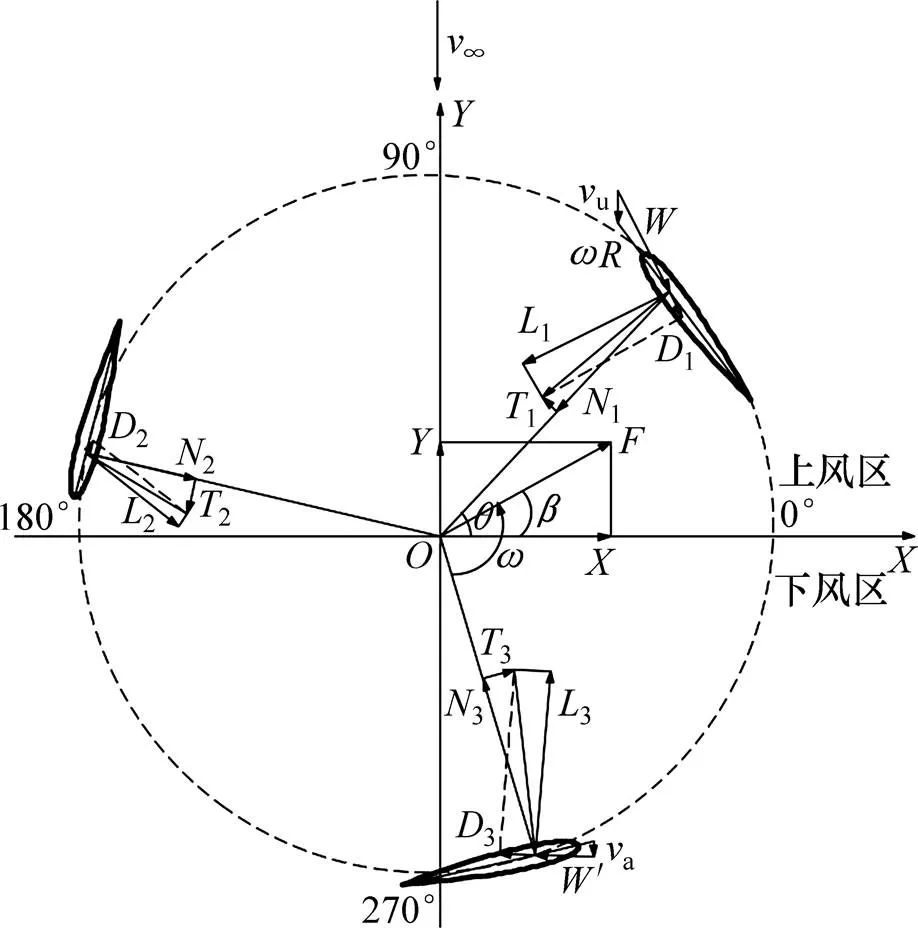
图2 叶片受力分析图

以叶片在上风区为例，分析图2中参数间的几何关系，可以得出垂直轴风轮的叶片攻角和合成风速的表达式为：

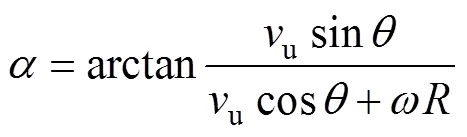
叶片所受的升力和阻力分别为

式中：为空气的密度，在标准大气压下常取为 1.247 kg/m3；为叶片弦长；Δ为所研究翼型的展向长度；L和D分别代表翼型的升力系数和阻力系数，其值可由NACA系列翼型空气动力学特性数据库 查得。

利用图2所示的几何关系，得到叶片切向运动的合力和垂直叶片切向运动的合力分别为：

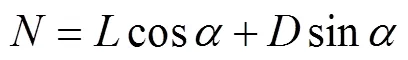
以3个叶片的风力机为例，将叶片上的气动力合成到主轴位置点处，首先将各叶片上的气动力分别分解到方向和方向，其各自的分量(1，2，3，1，2和3等参数下标表示不同的叶片)为：

再将方向和方向上的合力合成为主轴所受合力，其作用方向由与正方向的夹角表示：

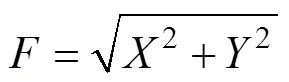
1.2 偏振效应

本文的研究对象为1.5 MW H型垂直轴风力发电机，相关参数[17]如表1所示，叶片翼型采用对称翼型NACA0015。

根据图2所示理论模型，风轮每旋转6°(流管数为30个)时，计算各叶片气动力。相邻2个叶片所受气动力的相位差为120°，可以通过计算其中1个叶片在不同方位角处的气动力，再通过相位变化，得出其余叶片所受的气动力。图3所示为风力机旋转1周，各叶片在不同时刻的气动力情况。从图3可以看出：在叶片旋转过程中，作用在风力机叶片上的气动力在任何时刻都不能互相抵消，由于合力不为0 N，将一直存在偏向力，产生偏向运动，且合力不能时刻相等，因而必然会产生振动。

表1 垂直轴风力发电机的参数

(a) 切向力；(b) 法向力

本文主要研究主轴上的振动，运用式(6)~(9)分析3个叶片所受的气动载荷在主轴上的合成作用，计算结果如图4所示。由图4可知：主轴受到的作用力一直存在，且大小、方向不定，主轴必然会偏移中心位置，并发生振动。这种因叶片旋转1周产生的气动力不稳定造成的主轴振动称为偏振效应。主轴所受合成力振荡幅度约为1 kN，作用位置的角度偏移幅度约为20°。

(a) 合成力大小；(b) 合成力方向

主轴振动力变化幅度可以用变差系数C来衡量。变差系数是1个相对差异量数，不受所衡量的数据的大小或单位影响。C越大，振动力波动越大，主轴振动幅度越大；C越小，振动力波动越小，主轴振动幅度越小。

式中：为标准差；为平均数。

2 风剪效应对主轴偏振的影响

风剪切是指在垂直方向上风速随高度的增加而变化，本文采用更加贴近实测值[18]的指数律进行研究：

图5 风速随高度变化的曲线

对于本文采用的H型1.5 MW垂直轴风力机，其风轮高度=30 m，所在区域范围较大，风速变化明显，故风剪效应不容忽视。考虑风剪效应，对主轴进行受力分析，结果如图6所示。

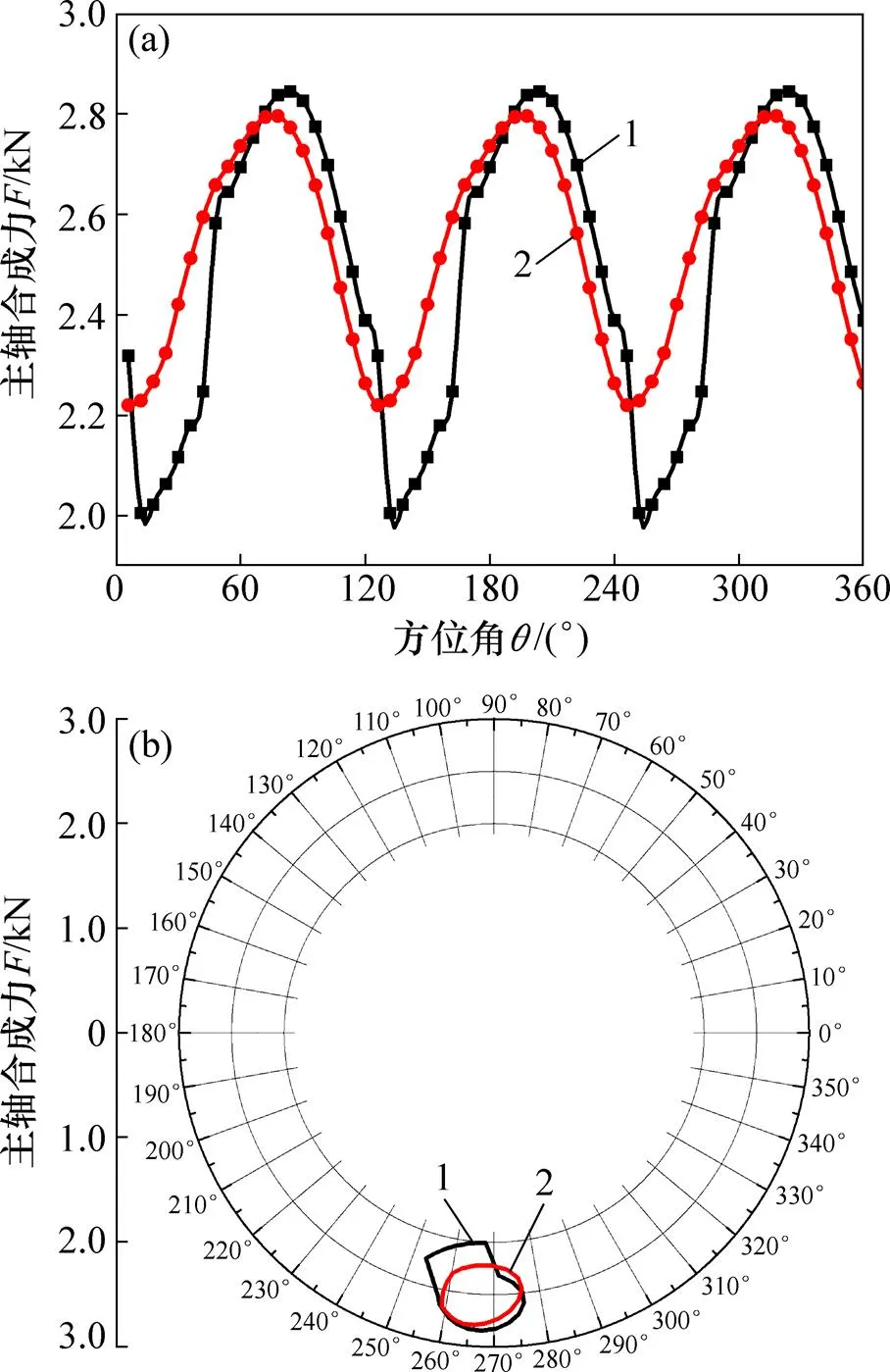
由图6可知：针对大型垂直轴风力机，考虑风剪效应存在的情况时，气动载荷作用在主轴位置上合力的振荡幅度降低，C从0.117 1降低到0.083 0，方向位置角度振荡幅度减小。因此，对于大型垂直轴风力机，从理论上来说，风剪效应会减小由于气动力载荷所引起的主轴振动。

3 叶片数量对主轴偏振的影响

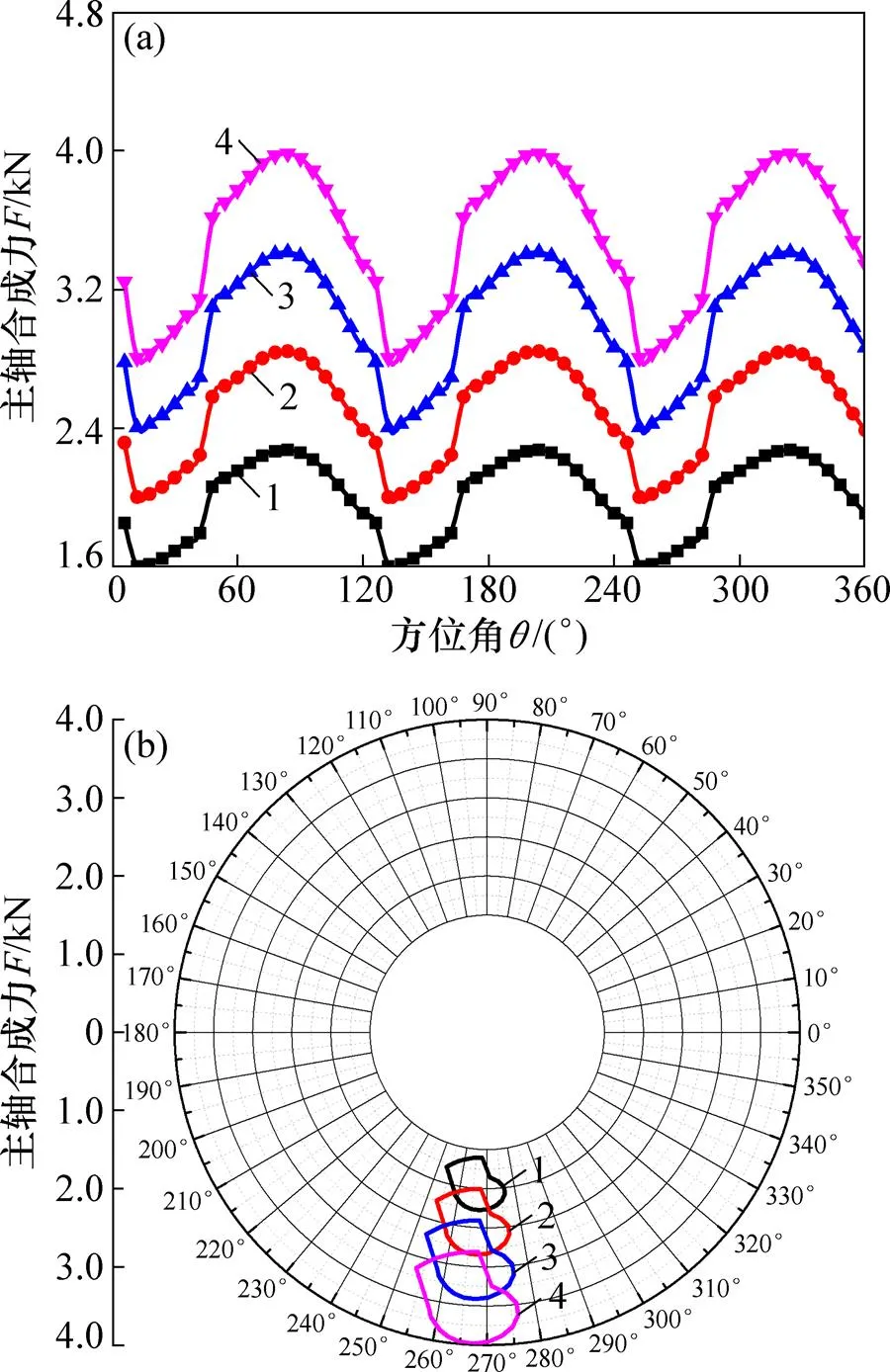
由于叶片数量必须为1个整数，因此，通过比对实际风机常见叶片数量的变差系数，以此分析叶片数量对主轴偏振的影响。分别计算当叶片数为2，3，4和5时，垂直轴风力机旋转一周主轴合成力的变化，结果如图7所示。由图7可以看到：当叶片数为3片时，主轴合成力幅度变化最小。分别计算各叶片数对应的衡量主轴合成力振荡幅度的变差系数C，结果如表2所示。由表2可知：当叶片数为3时，C最小。因此，考虑主轴振幅最小情况下，当风力机叶片数设置为3时，结果最佳。

(a) 风剪效应对合成力大小的影响；(b) 风剪效应对合成力作用位置的影响

N/片：1—2；2—3；3—4；4—5。

表2 不同叶片数量对应的振幅变差系数VC

4 高径比对主轴偏振的影响

风轮高径比为H型垂直轴风力机的风轮高度与风轮直径0的比值，记为=/0。风轮高径比关系到风力机的外形尺寸和制造成本，且对风力机气动性能有相当大的影响[20]。在保持风力机的扫掠面积0=2 040 m2(参照表1)不变、叶片数量为3的情况下，研究不同高径比对主轴偏振效应的影响。如图8所示，用变差系数C来衡量主轴偏振幅度。由图8可知：不同高径比对应的C不同，即所对应的主轴偏振幅度不同。并且从图8可以发现存在1个最佳高径比，使C最小，即主轴偏振幅度最小。为了得到最佳高径比，应使主轴偏振效应最小，对高径比进行优化计算。

具体优化计算过程如下(其中，为目标函数)：

计算结果显示，当高径比=0.508 8时，C= 0.080 4最小。针对最佳高径比风轮与原风轮(参照表1)，主轴合成力的对比结果如图9所示。由图9可以看出：相比原风力机参数，当高径比为0.508 8时，主轴合成力的振荡幅度、合成力方向的角度变化均减小。

(a) 高径比对合成力的影响；(b) 高径比对合成力作用位置的影响

5 展弦比对主轴偏振的影响

展弦比=/，是H型垂直轴风力机的叶片展向长度与叶片弦长的比值。提出2种改变风力机展弦比(叶片数0=3)的方案。

方案1：保持叶片弦长=3 m不变，通过改变叶片长度来改变展弦比。

方案2：保持叶片长度=30 m不变，通过改变叶片弦长来改变展弦比。

5.1 弦长不变，改变叶片长度

改变叶片长度，使展弦比为8，10，12，14，分别计算主轴合成力变化情况，计算结果如图10所示。由图10可以发现：通过改变叶片长度来改变展弦比，主轴合成力只是随着叶片长度的增加或减少(风力机扫掠面积的增大或减小)而增大或减小，其振荡幅度并没有产生变化，作用位置角度也没有变化。因此，保持叶片弦长不变，通过改变叶片长度来改变展弦比，对主轴偏振效应几乎没有影响。

(a) 展弦比对合成力的影响；(b) 展弦比对合成力作用位置的影响

5.2 叶片长度不变，改变弦长

在叶片数量为3，叶片长度为30 m(参照表1)时，改变叶片弦长，得到不同展弦比对应的主轴合成力变差系数C曲线，如图11所示。由图11可以看出：保持叶片长度不变，变化叶片弦长来改变风力机展弦比，此时不同展弦比所对应的C不同，即风力机偏振幅度不同，并存在最佳展弦比使C最小，即主轴振荡幅度最小。为了得到最佳展弦比，使主轴偏振效应最小，对展弦比进行优化，具体优化过程类似于高径比优化。

计算结果显示：当展弦比=14.201 5时，C最小，为0.056 1。针对最佳展弦比风轮与原风轮(参照表1)，主轴合成力对比结果如图12所示。由图12可以看出：相比原风力机参数，当展弦比为14.201 5时，主轴合成力的振荡幅度、合成力方向的角度变化均减小。

图11 不同展弦比对主轴偏振的影响(方案2)

(a) 展弦比对合成力的影响；(b) 展弦比对合成力作用位置的影响

6 结论

1) 针对1.5 MW垂直轴风力机，主轴位置存在作用力，且大小、方向不定，主轴必然会偏移中心位置，并发生振动，即产生偏振效应。针对所研究的垂直轴风力机，其主轴合成力大小振荡幅度约为1 kN，作用位置角度变化幅度约为20°。

2) 风剪效应使叶片气动载荷作用在主轴位置上的合力振荡幅度减小，变差系数C从0.117 1降低到0.083 0，方向位置角度变化幅度减小。因此，对于大型风力机，从理论上来说，风剪效应会减小由于气动力载荷引起的主轴偏振效应。

3) 叶片数量不同会对主轴偏振效应产生影响。当叶片数为3时，变差系数C=0.117 1最小，主轴发生的振动幅度最小。

4) 随着高径比的变化，主轴偏振效应变化趋势不规律。当高径比=0.508 8时，变差系数C=0.080 4，主轴发生的振动幅度最小。

5) 采用保持叶片长度不变，改变叶片弦长的方案来改变展弦比时，展弦比的变化会对主轴偏振效应产生影响。当展弦比=14.201 5时，变差系数C= 0.056 1，主轴发生的振动幅度最小。

[1] 田海姣, 王铁龙, 王颖. 垂直轴风力发电机发展概述[J]. 应用能源技术, 2006(11): 22−27. TIAN Haijiao, WANG Tielong, WANG Ying. Development of vertical axis wind turbine[J]. Application of Energy Technology, 2006(11): 22−27.

[2] LEUNG D Y C, YANG Y. Wind energy development and its environmental impact: a review[J]. Renewable & Unstainable Energy Reviews, 2012, 16(1): 1031−1039.

[3] 郭显义. 分析风力和太阳能光伏发电现状及发展趋势[J]. 中国商界, 2012(10): 421. GUO Xianyi. Analysis of the status and development trends of wind power and solar photovoltaic power generation[J]. Chinese Business Community, 2012(10): 421.

[4] 杨益飞, 潘伟, 朱熀秋. 垂直轴风力发电机技术综述及研究进展[J]. 中国机械工程, 2013, 24(5): 703−709. YANG Yifei, PAN Wei, ZHU Huangqiu. Review and research progress of vertical axis wind turbine[J]. China Mechanical Engineering, 2013, 24(5): 703−709.

[5] 何志宁, 刘座铭, 张宗珍. 垂直轴风力发电机的发展历史及现状[J]. 机械工程师, 2014(2): 39−40. HE Zhining, LIU Zuoming, ZHANG Zongzhen. The development history and present situation of vertical axis wind turbine[J]. Mechanical Engineer, 2014(2): 39−40.

[6] 李志萍. 对MW级风机液压变桨距控制技术的研究[J]. 科技与企业, 2015(6): 185−186. LI Zhiping. Research on the hydraulic pitch control technology of MW grade fan[J]. Science and Technology and Enterprises, 2015(6): 185−186.

[7] 李晔. 国外大型风力机技术的新进展[J]. 应用数学和力学, 2013, 34(10): 1003−1011. LI Ye. New development of large wind turbine technology in foreign countries[J]. Applied Mathematics and Mechanics, 2013, 34(10): 1003−1011.

[8] 史文博. H型垂直轴风电机组主轴系统结构分析方法的研究[D]. 重庆: 重庆大学机械工程学院, 2015: 7−8. SHI Wenbo. Study on the structure analysis method of the spindle system of the H vertical axis wind turbine[D]. Chongqing: Chongqing University. Mechanical Engineering College, 2015: 7−8.

[9] MATTHEW B T, CHRISTOPHER S M. Bearing selection techniques as applied to main shaft direct and hybrid drives for wind turbines[J]. The Timken company Technical Paper, 2009: 1−10.

[10] SOUICH Y, NOBUYUKI N. Technical trends in wind turbine bearings[J]. NTN Technical Review, 2008(76): 114−120.

[11] 韩德海. 风力发电机组主轴系统的结构分析研究[D]. 重庆: 重庆大学机械工程学院, 2009: 5. HAN Dehai. Study on the structure analysis of the main shaft system of the wind turbine[D]. Chongqing: Chongqing University. Mechanical Engineering College, 2009: 5.

[12] 霍玉玲. 有限元分析计算在矿井提升机上的应用[J]. 矿山机械, 2003(5): 34−35. HUO Yuling. Application of finite element analysis and calculation on mine hoist[J]. Mining Machinery, 2003(5): 34−35.

[13] 张婷婷. 大型垂直轴风机的优化、动力特性及疲劳研究[D]. 上海: 上海交通大学船舶海洋与建筑工程学院, 2009: 12. ZHANG Tingting. Study on the optimization, dynamic characteristics and fatigue of a large vertical shaft fan[D]. Shanghai: Shanghai Jiao Tong University. Marine and Architectural Engineering College, 2009: 12.

[14] 张婷婷, 王红霞, 代泽兵. 垂直轴风力机结构振动特性研究[J]. 华东电力, 2009, 37(3): 452−455. ZHANG Tingting, WANG Hongxia, DAI Zebing. Study on structural vibration characteristics of vertical axis wind turbine[J]. East China Electric Power, 2009, 37(3): 452−455.

[15] PARASCHIVOIU I.垂直轴风力机原理与设计[M]. 李春, 叶舟, 高伟, 译. 上海: 上海科学技术出版社, 2013: 124−140. PARASCHIVOIU I. Principle and design of vertical axis wind turbine[M]. LI Chun, YE Zhou, GAO Wei, trans. Shanghai: Shanghai Science and Technology Press, 2013: 124−140.

[16] 赵振宙, 陈潘浩, 陈景茹, 等. 基于双盘面多流管模型的升力型风轮气动性能改善分析[J]. 太阳能学报, 2017, 38(9): 2527−2534. ZHAO Zhenzhou, CHEN Panhao, Chen Jingru, et al. Research on aerodynamic characteristic of lift type wind turbine based on two-disk multy stream model[J]. Acta Energiae Solaris Sinica, 2017, 38(9): 2527−2534.

[17] 尹伟. 大功率直叶片垂直轴风力机气动特性及风轮构型研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2015: 17. YIN Wei. Aerodynamic characteristics and wind turbine configuration of a high power vertical blade vertical axis wind turbine[D]. Harbin: Harbin Institute of Technology. Mechanical Engineering College, 2015: 17.

[18] 张国铭. 论制造兆瓦级垂直轴风力发电机的合理性[J]. 风力发电, 2001(4): 55−61. ZHANG Guoming. On the rationality of producing megawatt vertical axis wind turbines[J]. Wind Power Generation, 2001(4): 55−61.

[19] 张玉良, 杨从新, 李仁年, 等. 风剪切对风力机设计的无关性分析[J]. 西华大学学报(自然科学版), 2007, 26(2): 61−63. ZHANG Yuliang, YANG Congxin, LI Rennian, et al. Unrelated analysis of wind shear to wind turbine design[J]. Journal of Xihua University(Natural Science Edition), 2007, 26(2): 61−63.

[20] 杨从新, 李振朋, 史广泰. 高径比对垂直轴风力机气动性能的影响[J]. 新技术新工艺, 2013(11): 86−88. YANG Congxin, LI Zhenpeng, SHI Guangtai. Influence of height diameter ratio on aerodynamic performance of vertical axis wind turbine[J]. New Technology and New Technology, 2013(11): 86−88.

Influence of aerodynamic parameters of vertical axis wind turbine on vibration effect of main shaft

ZHANG Lijun, MI Yuxia, ZHAO Xinhui, MA Dongchen, MA Wenlong, WANG Hanxiang, LIU Jing

(School of Electromechanical Engineering, China University of Petroleum, Qingdao 266580, China)

The mechanism of the vibration effect of the main shaft of a 1.5 MW H-type vertical axis wind turbine(VAWT) with the symmetrical wing was analyzed according to the double-multiple stream tubes theory. The variation coefficient was proposed and used to measure the oscillation degree of the synthetic force on the main shaft, and the influence of wind turbine parameters on the vibration effect was analyzed. The results show that the synthetic force on the main shaft, which is produced by the blade in a cycle of operation, is wavy and cannot counteract each other. For huge vertical axis wind turbine, the wind shear effect is beneficial to reducing the vibration effect. For the design of H-type vertical axis wind turbine, when the number of blades is three, the vibration amplitude of the main shaft is the smallest; when the height diameter ratio is 0.508 8, the vibration amplitude of the main shaft is the smallest; the vibration amplitude of the spindle is the smallest when the aspect ratio is 14.201 5.

vertical axis wind turbine(VAWT); vibration effect; wind shear effect; aspect ratio

10.11817/j.issn.1672−7207.2018.12.025

KT83

A

1672−7207(2018)12−3105−08

2017−12−12；

2018−03−13

国家自然科学基金资助项目(51707204）；中央高校基本科研业务专项(17CX05021)(Project(51707204) supported by the National Natural Science Foundation; Project(17CX05021) supported by the Fundamental Research Funds for the Central Universities)

张立军，博士，教授，硕士生导师，从事可再生能源技术和绿色装备制造研究；E-mail：zhanglijun@upc.edu.cn

(编辑 刘锦伟)