基于混沌系统和动态DNA编码与运算的彩色图像加密算法
杨吉云,吴 昊
(重庆大学 计算机学院,重庆 400044)
0 概述
随着数字技术和通信网络的发展,越来越多的数字信息需要通过网络传输。由于数字图像具有直观、生动等特点,已成为应用最广泛的一种数字信息,但其也面临着日益严重的安全威胁。数字图像加密技术是一种有效保护数字图像安全的方法,由于混沌加密技术具有实现简单、鲁棒性好、加密速度快、安全性高等特点,经过多年的发展,已被应用于图像加密技术研究中[1-3]。文献[1]提出一种基于置乱扩散结构的采用时空混沌系统的图像加密算法。文献[2]提出了一种提出了基于多维混沌系统同时对图像像素位置置乱和像素值加密的新算法。但安全性分析表明,混沌加密技术保护图像安全性的能力还需进一步提高[4-5]。文献[4]指出加密算法对于明文改变的低敏感性使得攻击者易于采用选择明文攻击破解加密算法的置乱过程。文献[5]研究发现当密钥与明文无关及加密过程中各像素相互独立,算法无法有效抵抗已知明文和选择明文攻击。
文献[6]中首次提出了DNA计算,其具有超大规模并行性、超低的能量消耗和超高的存储密度等优点。DNA计算作为提高混沌图像加密技术安全性的有效途径,已被一些学者应用于混沌图像加密方案。文献[7]将DNA序列操作应用到了加密算法的置乱和扩散过程,有效提高了算法抵抗明文攻击的能力。文献[8]在置乱和扩散阶段有效结合混沌序列的随机性和DNA编码的特性,扩大了算法的密钥空间并且提高了抵抗统计攻击的能力。
然而,当前结合混沌系统和DNA计算的图像加密算法也存在不足之处。文献[9]通过对加密算法数学模型的分析,找到了加密系统中存在的线性关系,通过对加密算法进行等价代换,一方面减小了算法密钥空间,削弱了算法抵抗穷举攻击的能力,另一方面针对算法采用单一的编码规则和运算规则的缺陷,运用选择明文攻击获取了算法的等价密钥。文献[10]指出了采用固定编码和单一运算规则的DNA混沌图像加密算法容易通过选择明文攻击进行破解。
针对上述DNA混沌图像加密算法中存在的不足,本文结合混沌系统和DNA计算,通过用Intertwining Logistic映射产生的随机序列值动态选择彩色图像R、G、B信道每个像素在进行DNA加密计算时所采用的编码规则和运算规则,避免算法因采用固定编码规则和单一运算规则而导致易被破解的缺陷。采用模拟退火算法构造置乱序列分别对R、G、B信道行和列进行充分置乱,再结合混沌映射通过动态DNA计算对图像进行扩散,消除加密系统中存在的线性关系,并解决算法抵御穷举攻击及明文攻击能力弱的问题。
1 混沌系统及DNA编码
1.1 Intertwining Logistic映射
Intertwining Logistic映射可被描述为以下形式:
(1)
其中,0<μ≤3.999,|k1|>33.5,|k2|>37.9,|k3|>35.7。Intertwining Logistic映射比Logistic映射具有更优秀的混沌特性,且因其没有空白窗口而具有更好的特性[11],如图1所示。
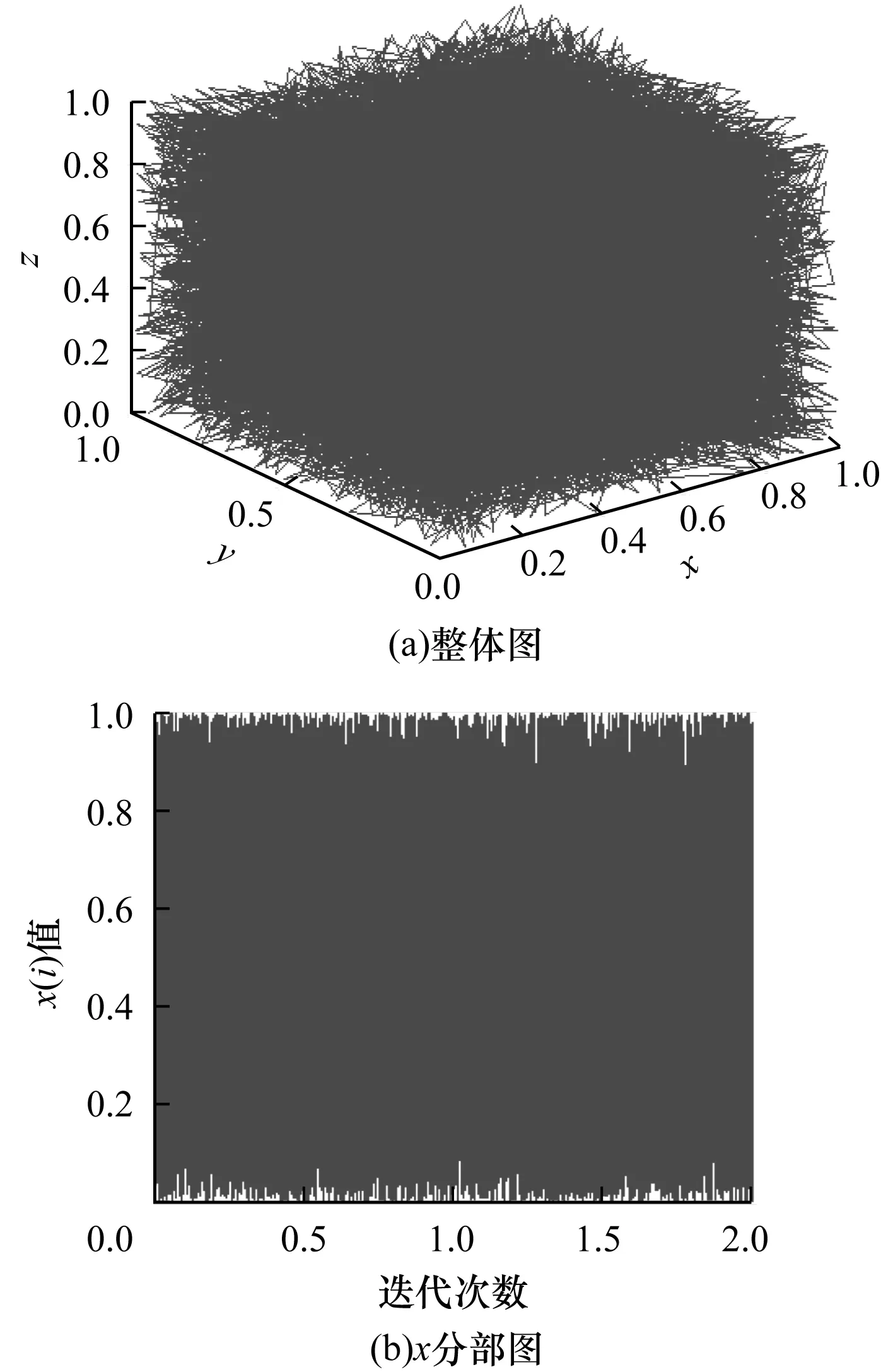
图1 Intertwining Logistic映射
1.2 DNA编码
一个DNA序列由A、T、C、G 4种核酸碱基组成,其中,A与T,C与G互补配对。二进制序列中0与1互补,因此可以使用A、C、G、T编码00、01、10、11,根据 Watson.Crick互补规则[12]有8中编码规则符合要求,如表1所示。另外,根据编码规则0定义的DNA加法、减法和异或操作,分别如表2~表4所示。
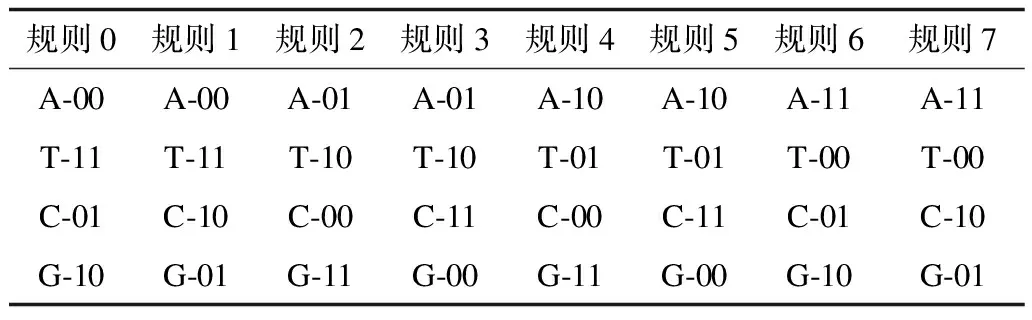
表1 DNA编码规则

表2 DNA加法运算规则
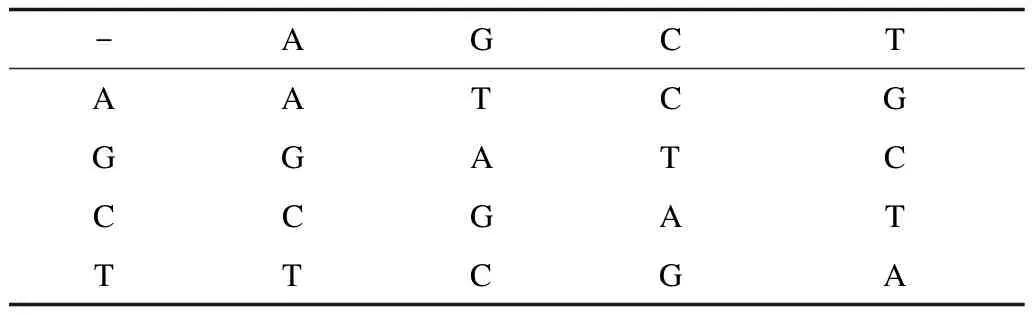
表3 DNA减法运算规则
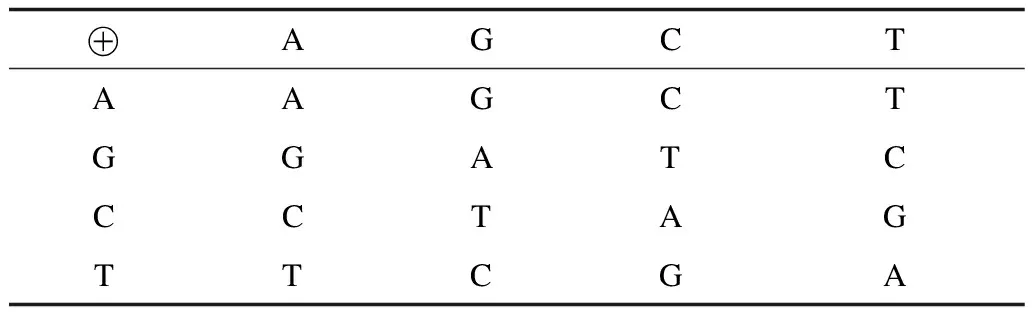
表4 DNA异或运算规则
2 算法描述
2.1 图像加密算法概述
本文算法由2个阶段组成:行列置乱阶段和DNA加密扩散阶段。第1阶段利用Intertwining Logistic映射产生随机序列,将其与模拟退火算法相结合构造出置乱序列,然后对图像进行置乱。第2阶段通过Intertwining Logistic映射产生随机序列,先根据随机序列值对图像进行DNA编码并选择运算规则,再进行DNA加密计算。算法加密流程如图2所示。
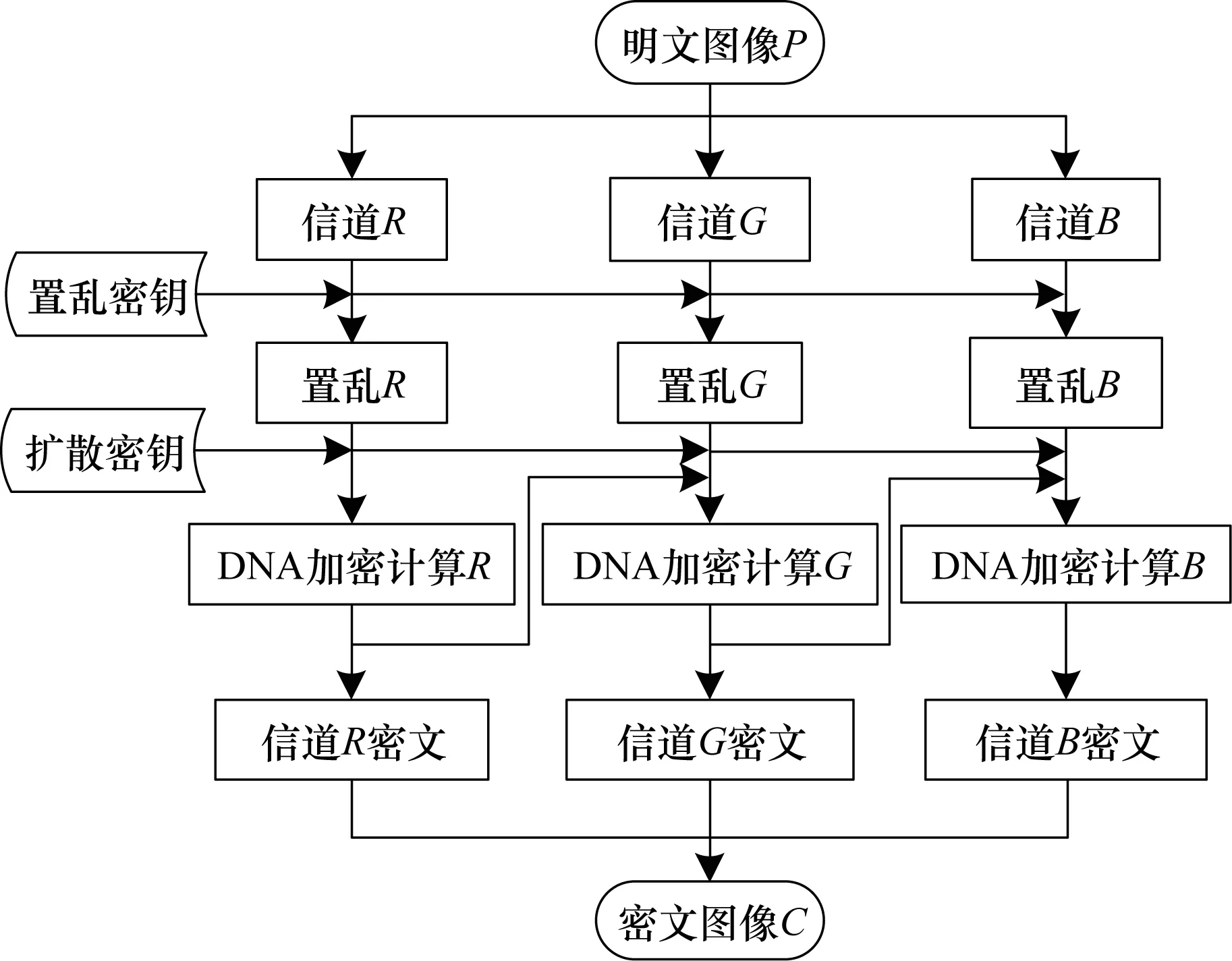
图2 本文算法加密流程
2.2 图像加密过程
算法的具体执行过程如下所示。
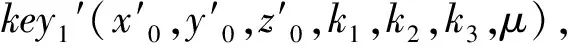
(2)
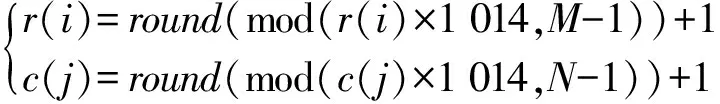
(3)
式(2)中sumr,sumg,sumb分别为各信道像素和。
步骤2对于信道R,借鉴文献[13]采用模拟退火算法(SA)构造无序序列的方法,将r1、r2和1,2,…,M作为SA输入值,构造行置乱序列u1,u2,…,uM,其中ui∈[1,M]。同样用c1、c2和1,2,…,N构造列置乱序列v1,v2,…,vN,其中vi∈[1,N]。采用相同方法为信道G和B构造置乱序列。
步骤3R信道中先把第1,2,…,M行重新置于第u1,u2,…,uM行,再将第1,2,…,N列重新置于第v1,v2,…,vN列,获取置乱信道R′。同理获取信道G、B的置乱信道G′、B′。

l(i)=floor(mod(l(i)×1 014,256))
(4)
在DNA加密计算过程中随机序列与信道序列的DNA编码方式和计算规则选取如下所示。
1)DNA编码。由表1可知,DNA编码有8种不同规则,在DNA加密计算中,由随机序列值l(i)根据式(5)确定每个信道序列和随机序列第i个值的编码规则rule。编码时将随机序列值和信道序列值分别转换为8位二进制序列,再将二进制序列转换为由4个碱基组成的DNA序列。
rule=mod(l(i),8)
(5)
2)计算规则的选取。本文算法中DNA计算公式如式(6)所示,其中P(i) 为信道序列第i个值的DNA序列,C(i)为P(i)的密文 DNA序列,C(i-1)为密文对应的前一个密文DNA序列,L(i)为随机序列第i个值的DNA序列。运算规则frule(*,·)定义如表5所示,其中DNA运算规则frule由l(i)根据式(7)确定。
C(i)=P(i)×C(i-1)·L(i)
(6)
frule=mod(l(i),9)
(7)

步骤5由式(8)获得sumc0,根据其值利用式(5)将其编码为初始DNA密文C0。将C0作为PR初始密文CR(0),依次先根据LR的元素LR(i)把PR(i)和LR(i)编码成长为4的DNA序列并选取运算规则,再利用式(6)进行DNA加密计算获取CR(i),最后获得长M×N×4的PR密文DNA序列CR,其中,i=1,2,…,MN。将CR(MN)作为PG初始密文,进而获得CG;然后将CG(MN) 作为PB初始密文,计算CB。
sumc0=mod((sumr+sumg+sumb),256)
(8)
步骤6将3个密文序列根据对应随机序列值利用式(5)选择编码规则进行解码,然后转换为3个M×N的密文矩阵,合并3个矩阵得到密文图像C。
2.3 图像解密过程
解密算法为加密算法的逆,具体过程如下:
步骤1使用扩散密钥获取随机序列LR、LG、LB,利用式(4)使其值l(i)∈[0,255](i=1,2,…,MN)。再将密文图像C各信道转化为长M×N的一维密文信道序列。
步骤2每个密文信道序列和随机序列的每个值依次根据l(i)编码为DNA序列,再用l(i)选取的计算规则利用式(6)的逆运算获取每个密文信道中每个密文的明文DNA序列。各密文信道序列计算完成后分别得到长度为M×N×4的明文DNA序列。
步骤3根据l(i)选取编码规则将3个明文DNA序列解码为长M×N的一维置乱信道序列PR、PG、PB,再将其转化为M×N的二维置乱信道R′、G′、B′。
步骤4运用置乱密钥获取随机序列,然后采用SA构造行列置乱序列,将R′、G′、B′行和列的位置根据置乱序列反向重排列,从而得到恢复像素R、G、B。最后合并R、G、B信道得到解密后的原始图像P。
3 仿真实验
在Windows7 64位系统环境下使用MATLAB软件,运用本文算法对标准512像素×512像素的Lena.bmp和Baboon.bmp彩色图像进行加密和解密。选用的密钥如表6所示,实验结果如图3所示。

表6 加密和解密密钥

图3 加密解密效果
通过观察图3可以看出加密后的图像没有显示任何明文信息。通过比较原始图像图3(a)、图3(d)和解密图像图3(c)、图3(f)的所有像素点可知,2个图像像素点的值完全相同,说明本文提出的算法在加密和解密过程中没有丢失图像的任何信息。
4 安全性分析
4.1 密钥空间
本文算法的密钥由Intertwining Logistic映射在2个加密阶段的初始值及参数和t组成,即表6所示的置乱密钥key1和扩散密钥key2。根据文献[14]和IEEE Standard 754-2008 存储密钥采用的类型为双精度浮点型,其使用8 Byte对数据进行存储,密钥精度为10-15,因此,本文算法密钥长度为960 bit,密钥空间可达2960≈9.75×10288。由文献[15]可知本文的密钥空间可以很好地抵抗各种类型的穷举攻击并且提高加密系统的安全性。
4.2 密钥敏感性
对表6所示的密钥key1、key2,在此仅仅将key2中的μ做一个微小的改变,即μ=μ+ 10-15,其余密钥保持不变得到一个改变后的密钥key2′,然后用key1、key2′对key1、key2加密的图像进行解密。图4给出了key1、key2和key1、key2′的解密结果,从图中可以看出key1、key2′无法正确解密密文图像,说明本文算法对密钥具有极强的敏感性。

图4 密钥敏感性分析
4.3 相邻像素相关性分析
随机选取Lena和Baboon的R、G、B信道明文和密文图像中5 000对相邻像素点,分别进行水平、垂直、对角3个方向的相关性统计测试,测试结果如表7所示。
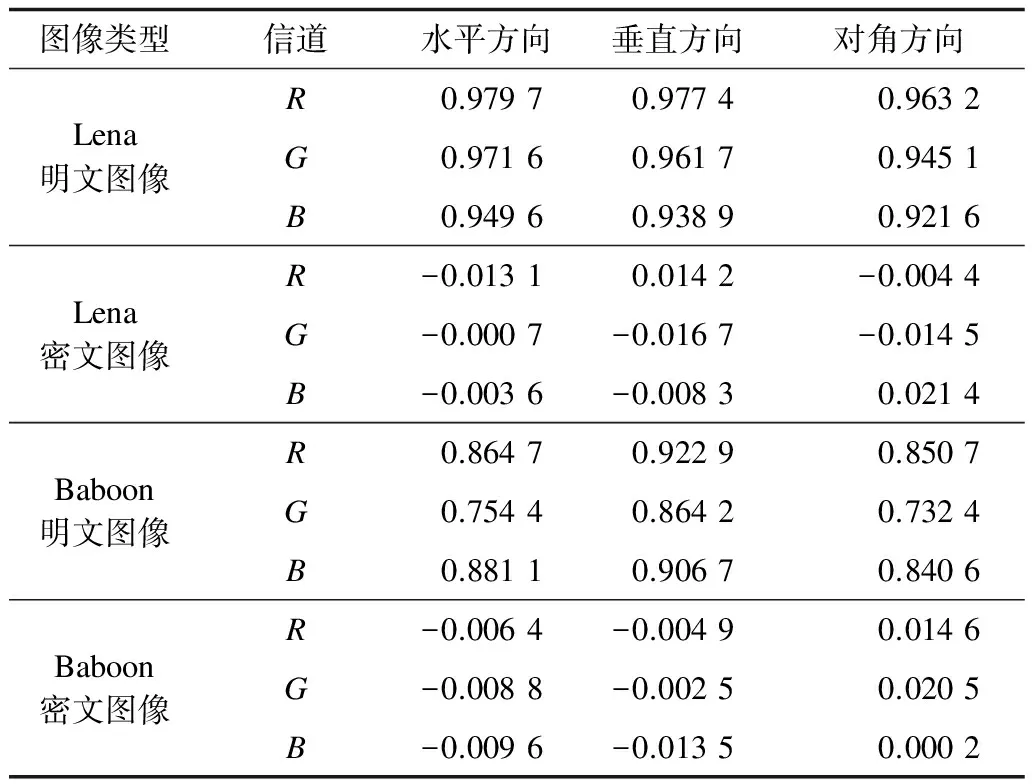
表7 明文、密文图像R、G、B信道的相关性系数
相关性计算公式如下:
(9)
(10)
(11)
(12)
从表7可以看出,Lena和Baboon的明文图像相关系数均接近于1,密文图像相关性系数均接近于0。其中Lena图像中选取的水平方向上5 000对相邻像素点分布情况如图5所示。
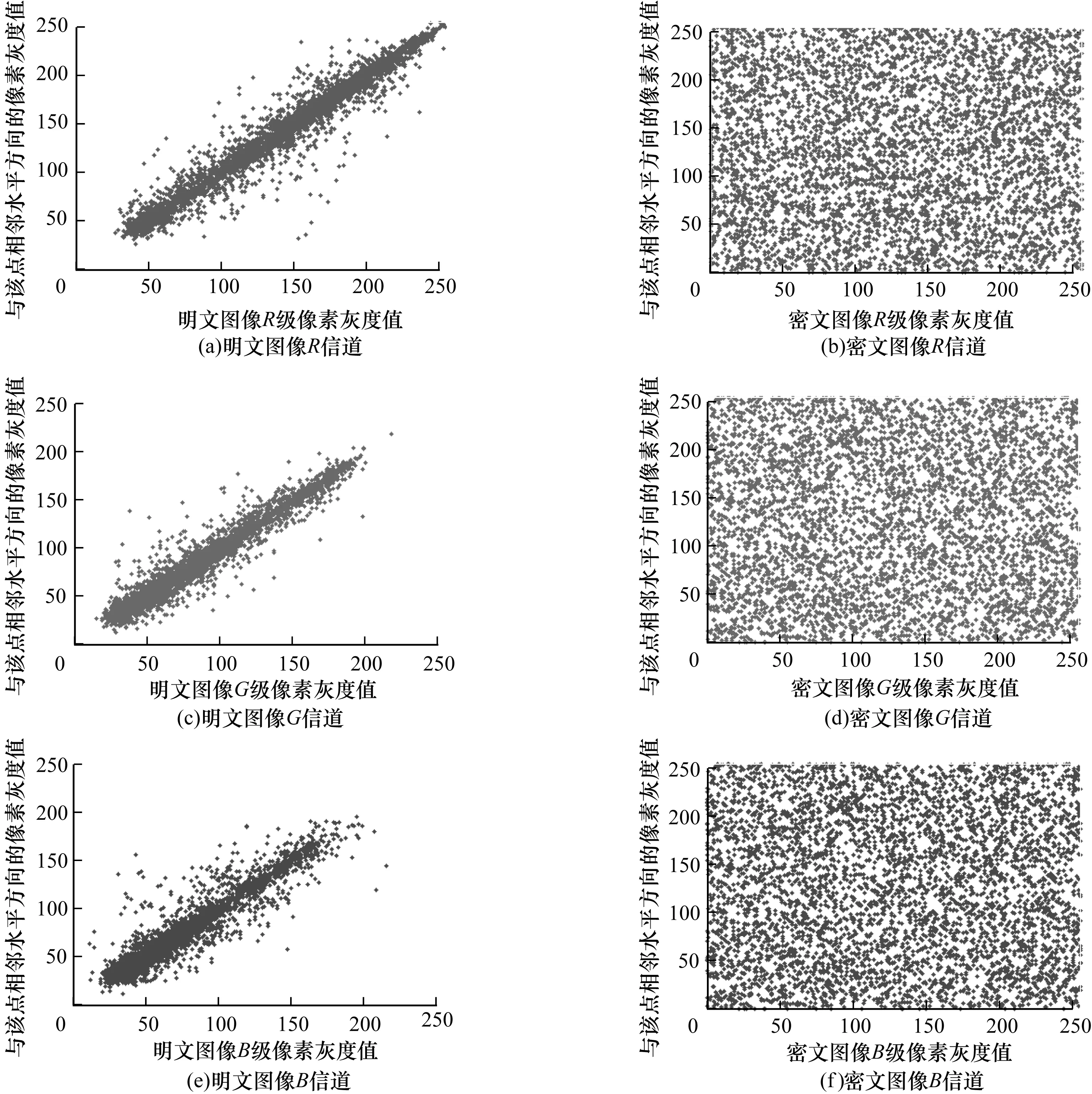
图5 Lena水平方向相邻像素相关性分析
可以看出,明文图像相邻像素点连续分布,密文图像相邻像素点值随机分布且布满整个二维空间。由以上可知,密文图像已基本消除了相邻像素的相关性且掩盖了原始图像的数据特征。
4.4 直方图分析
图6为Lena图像R、G、B信道的明文和密文频率直方图,其中图6(a)、图6(c)、图6(e)分别是明文图像直方图,图6(b)、图6(d)、图6(f)分别是密文图像直方图。通过比较直方图能够发现,明文图像的像素值都集中在一些值上,而密文图像的像素值是均匀分布的,这些均匀分部的密文像素值能够较好的抵抗统计攻击。
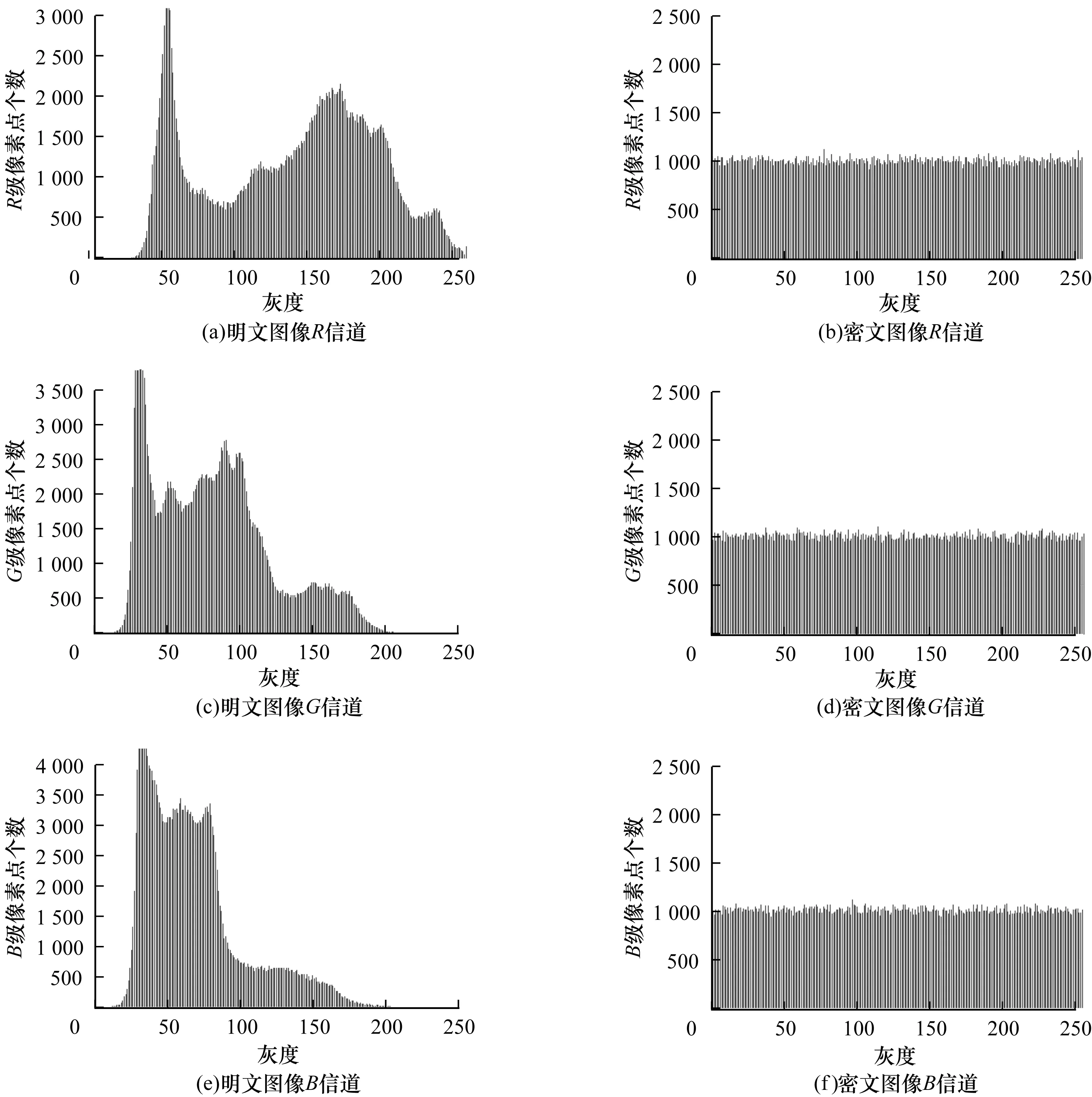
图6 Lena图像直方图
4.5 信息熵分析
信息熵可以判断元素的随机性,图像信源的熵值越接近8,图像信息的随机性就越强。对Lena密文图像的每个信道计算信息熵结果见表8,计算公式如下:
(13)
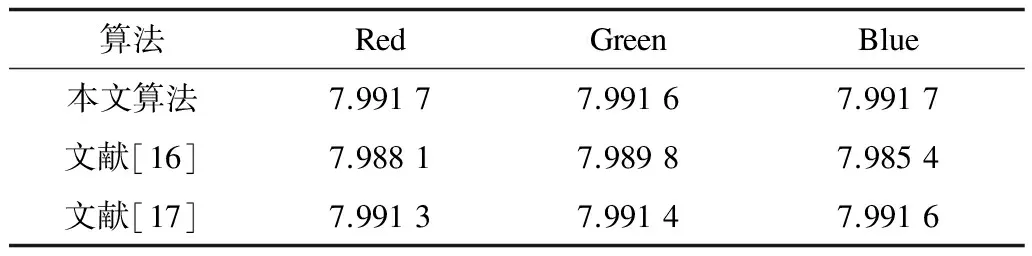
表8 Lena密文R、G、B信道图像信息熵
由表8可以看出,本文算法加密后图像的信息熵均接近8,与文献[16-17]相比本文具有更大的熵值,因此,证明本文算法加密后密文中各像素点值具有更强的随机性,能有效地抵御熵攻击。
4.6 抗差分攻击能力分析
加密算法抗差分攻击的能力可以用像素数改变率NPCR(Number of Pixels Change Rate)和归一化像素值平均改变强度UACI(Unified Average Changing Intensity)来度量,计算公式如下:
(14)
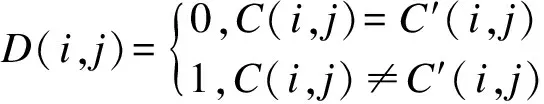
(15)
(16)
在Lena明文图像中随机选择一个像素,改变其像素值,根据式(14)~式(16)进行100组的实验后,计算得到NPCR和UACI的平均值如表9所示,表中也展示了其他彩色图像加密算法的实验结果。
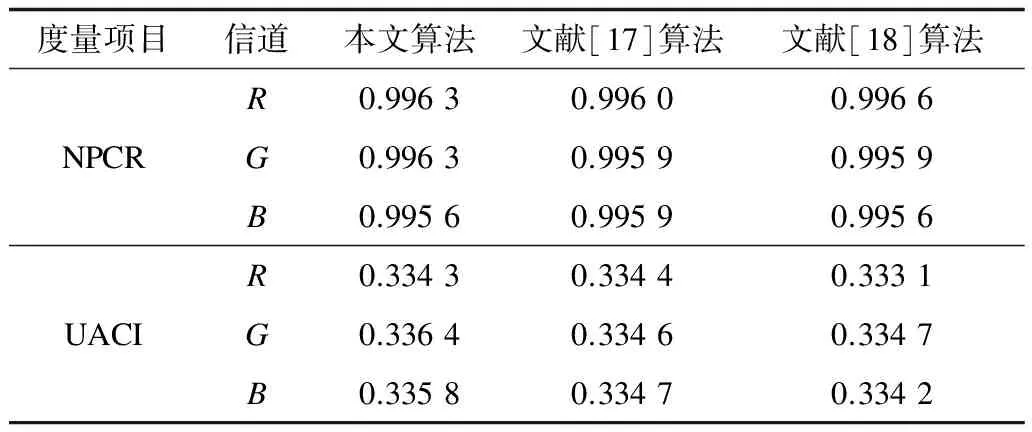
表9 NPCR与UACI度量数据
由表9可以看出,本文算法各分量的NPCR均超过0.99,UACI均超过0.33,且与文献[17-18]对比可以看出,本文总体上具有更大的NPCR和UACI,可知本文算法具有良好的抗差分攻击能力。
4.7 已知明文和选择明文攻击
在已知明文和选择明文攻击中,攻击者通常会对明文图像做一些微小的改变并观察相应的密文图像或者选择特殊的明文图像(比如各像素点都相同的明文图像)进行加密来获取密钥信息。通过实验可以看出本文算法对明文极其敏感,任意改变明文图像一个像素将获得几乎完全不同的密文图像。在加密过程中,步骤1和步骤4采用式(2)利用初始密钥和明文图像重新计算了混沌映射的初值,因此攻击者使用特殊明文获取的密钥对于其他已加密的明文图像来说是无效的。另外,在步骤5中初始密文DNA序列也由明文图像确定,不同的明文图像生成不同的初始序列。
本文算法在步骤5中运用式(6)计算密文C(i)时P(i)和L(i)的DNA编码及采用的计算规则都是动态变化的,当明文发生变化时加密过程中所采用的编码规则和计算规则也相应发生变化。在DNA加密计算过程中还采用了密文反馈机制,一方面计算每个像素点密文时会受到前面所有密文的影响,另一方面使得明文图像各信道在加密过程中互相影响。
因此,通过采取以上措施,本文算法抵抗已知明文和选择明文攻击的能力得到了有效提高。
5 结束语
本文提出一种结合Intertwining Logistic映射和动态DNA编码与运算的图像加密算法。首先在对明文图像置乱和扩散过程中使密文与密钥、明文的关系复杂化,并且2个阶段的密钥都依赖于明文,增强算法对明文的敏感性。其次在DNA计算中编码规则和运算规则的动态变化提高了算法抵抗已知明文和选择明文及穷举攻击的能力。在加密过程中,2个阶段都融合了混沌系统的随机性,并且扩散阶段在彩色图像R、G、B各信道内及信道间还采用了密文反馈机制,有效增强了算法的安全性和可靠性。通过安全性分析可以看出,该算法密钥空间大,对图像置乱扩散效果良好,能够抵抗常见的攻击。下一步将在实际应用中进一步优化时间复杂度,提高运行速度。
[1] ZHANG Xuanping,ZHAO Zhongmeng.Chaos-based Image Encryption with Total Shuffling and Bidirectional Diffu-sion[J].Nonlinear Dynamics,2014,75(1/2):319-330.
[2] 朱从旭,李 力,陈志刚.基于多维混沌系统组合的图像加密新算法[J].计算机工程,2007,33(2):142-144.
[3] MOLLAEEFAR M,SHARIF A,NAZAR M.A Novel Encryption Scheme for Colored Image Based on High Level Chaotic Maps[J].Multimedia Tools & Applications,2017,76:1-23.
[4] JENG Fuhgwo,HUANG Weilun,CHEN Tzungher.Cryptanalysis and Improvement of Two Hyper-chaos-based Image Encryption Schemes[J].Signal Processing:Image Communication,2015,34:45-51.
[5] XIAO Di,LIAO Xiaofeng,WEI Pengcheng.Analysis and Improvement of a Chaos-based Image Encryption Algorithm[J].Chaos Solitons & Fractals,2009,40(5):2191-2199.
[6] ADLEMAN L.Molecular Computation of Solutions to Combinatorial Problems[J].Science,1994,266(5187):1020-1024.
[7] HUANG Xiaoling,YE Guodong.An Image Encryption Algorithm Based on Hyper-chaos and DNA Sequence[J].Multimedia Tools & Applications,2014,72(1):57-70.
[8] SONI A,KUMAR A A.A Novel Image Encryption Approach Using an Index Based Chaos and DNA Encoding and Its Performance Analysis[J].International Journal of Computer Applications,2012,47(23):1-6.
[9] BELAZI A,HERMASSI H,RHOUMA R,et al.Algebraic Analysis of a RGB Image Encryption Algorithm Based on DNA Encoding and Chaotic Map[J].Nonlinear Dynamics,2014,76(4):1989-2004.
[10] OZKAYNAK F,YAVUZ S.Analysis and Improvement of a Novel Image Fusion Encryption Algorithm Based on DNA Sequence Operation and Hyper-chaotic System[J].Nonlinear Dynamics,2014,78(2):1311-1320.
[11] SHATHEESH S I,DEVARAJ P,BHUVANESWARAN R S.An Intertwining Chaotic Maps Based Image Encryption Scheme[J].Nonlinear Dynamics,2012,69(4):1995-2007.
[12] WATSON J D,CRICK F H.Molecular Structure of Nucleic Acids[J].Nature,1953,171(25):737-738.
[13] WANG Xingyuan,LIU Chuanming,Xu Dahai,et al.Image Encryption Scheme Using Chaos and Simulated Annealing Algorithm[J].Nonlinear Dynamics,2016,84(3):1417-1429.
[14] BORIGA R,DASCALESCU A C,DIACONU A.A New One-dimensional Chaotic Map and Its Use in a Novel Real-time Image Encryption Scheme[J].Advances in Multimedia,2014(7):1-15.
[15] NOROUZ B,SEYEDZADEH S M,MIRZAKUCHAKI S,et al.A Novel Image Encryption Based on Row-column,Masking and Main Diffusion Processes with Hyper Chaos[J].Multimedia Tools and Applications,2015,74(3):781-811.
[16] LIU Shubo,SUN Jing,XU Zhengquan.An Improved Image Encryption Algorithm Based on Chaotic System[J].Journal of Computers,2009,4(11):1091-1100.
[17] KADIR A,AILI M,SATTAR M.Color Image Encryption Scheme Using Coupled Hyper Chaotic System with Multiple Impulse Injections[J].Optikinternational Journal for Light and Electron Optics,2017,129:231-238.
[18] TONG Xiaojun,CUI Minggen.Image Encryption Scheme Based on 3D Baker with Dynamical Compound Chaotic Sequence Cipher Generator[J].Signal Processing,2009,89(4):480-491.

