新疆奎屯河流域平原区地下水质量评价方法探讨
陈和军
(新疆地矿局第二水文工程地质大队,新疆昌吉831100)
多年以来,在评价某一区域的地下水质量时,选用的方法因评价者个人的喜好和实际资料条件的限制而有所不同,至于何种评价方法具有较高的准确性,更能贴近实际情况,目前尚无明确的定论。而且,除地下水质量和生活饮用水质量国家颁布标准外,对评价方法无具体规定。本文以奎屯河流域平原区为例,运用多种方法对该地区地下水质量进行评价,以比较各种方法的优点和不足。
1 评价标准
各种评价方法的评价标准应有一个统一的尺度,以便于各种评价方法结果的分析对比,判断不同方法的优缺点和适用性。本文采用《地下水质量标准》(GB/T14848-93)中的分级标准作为各种方法的评价标准。见表1。
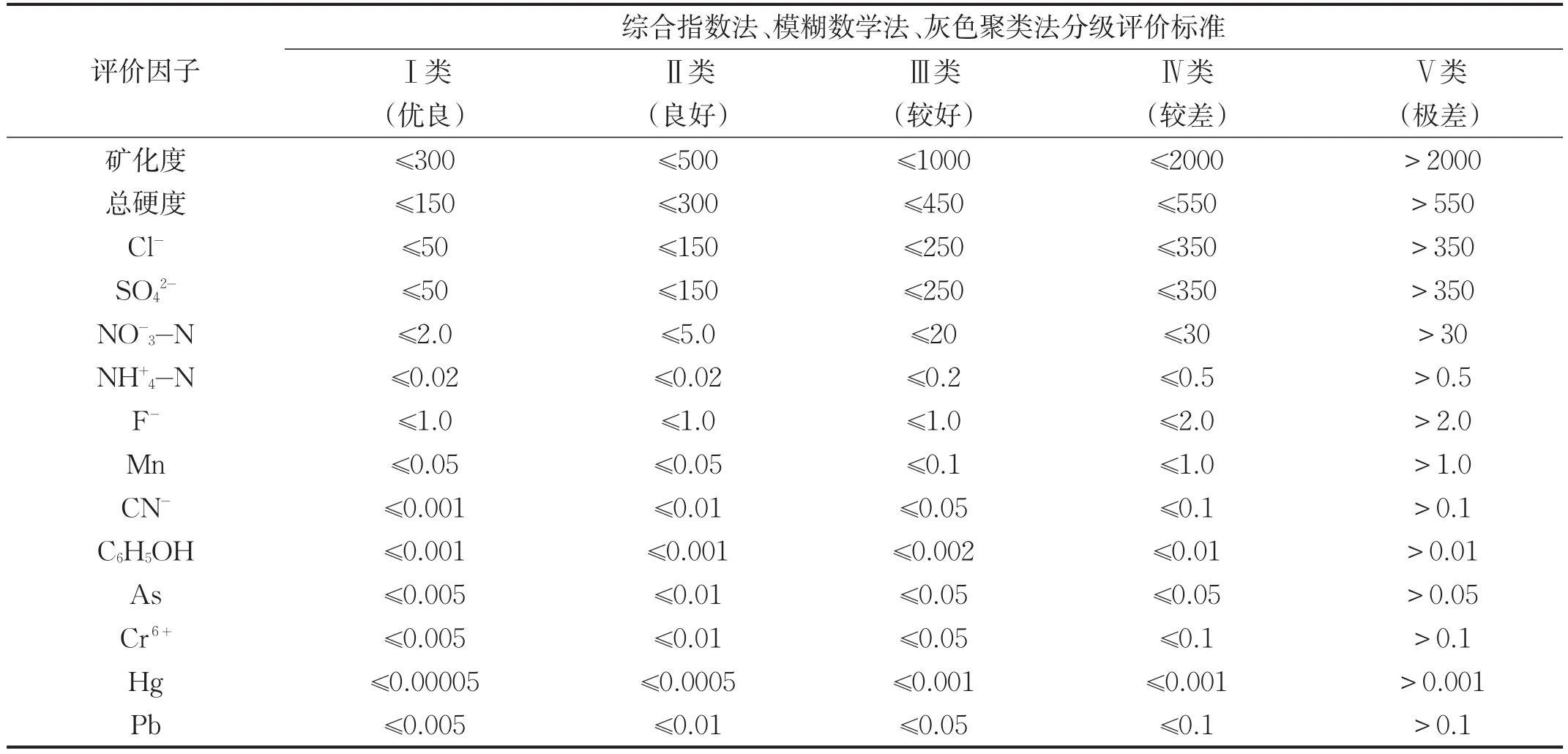
表1 地下水质量评价等级表(单位:mg/L)
2 评价因子的选择
地下水水化学成分不仅与原生的地质环境有关,亦与外部影响因素(如人类活动)有关,在充分考虑反映本地区地下水类型和性质的常规化学组分外,又兼顾区域地质环境中所特有的对人体健康有重要影响的组分及人类活动可能造成的某些污染组分,确定总硬度、矿化度、SO42-、Cl-、NO3--N、NH+4-N、F-、CN-、C6H5OH、As、Mn、Cr6+、Hg、Pb等14项指标作为评价因子参与地下水质量的评价。
3 评价方法
3.1 浓度法
此种方法是根据水质监测点的分析结果,用参与评价因子的检出率和超标率来对评价地区的地下水做出评价。
检出率=(检出的某种因子的监测点数量/某种因子的监测点总数)×100%
超标率=(超标的某种因子的监测点数量/某种因子的监测点总数)×100%
3.2 综合指数法
3.2.1 各单项组分评价
首先进行各单项组分评价,根据单项组分实际检测值,对照表1划分组分所属质量类别,不同类别标准值相同时,从优不从劣。按表2分别确定单项组分评价的评分值Fi。

表2 地下水水质类别单项组分分值表
3.2.2 综合评价
计算综合评价分值F,按表3划分地下水质量级别。

表3 地下水质量综合评价分级表
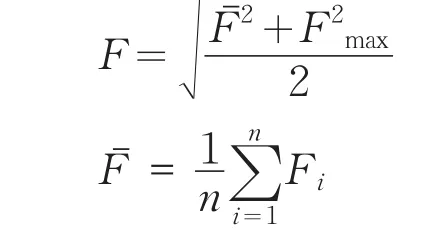
Fmax——各单项组分评分值Fi的最大值;
n——参与评价单项组分数。
3.3 灰色聚类法
3.3.1 确定灰类白化函数
灰类白化函数(fj)是表征聚类指标(评价因子j)对聚类灰数(灰类k,k=Ⅰ,Ⅱ,…,Ⅴ)归属度的函数,一般用线性灰类白化函数(见图1),灰类白化函数一般用图解法和线性关系确定,本文采用以下关系式确定:

图1 线性灰类白化函数
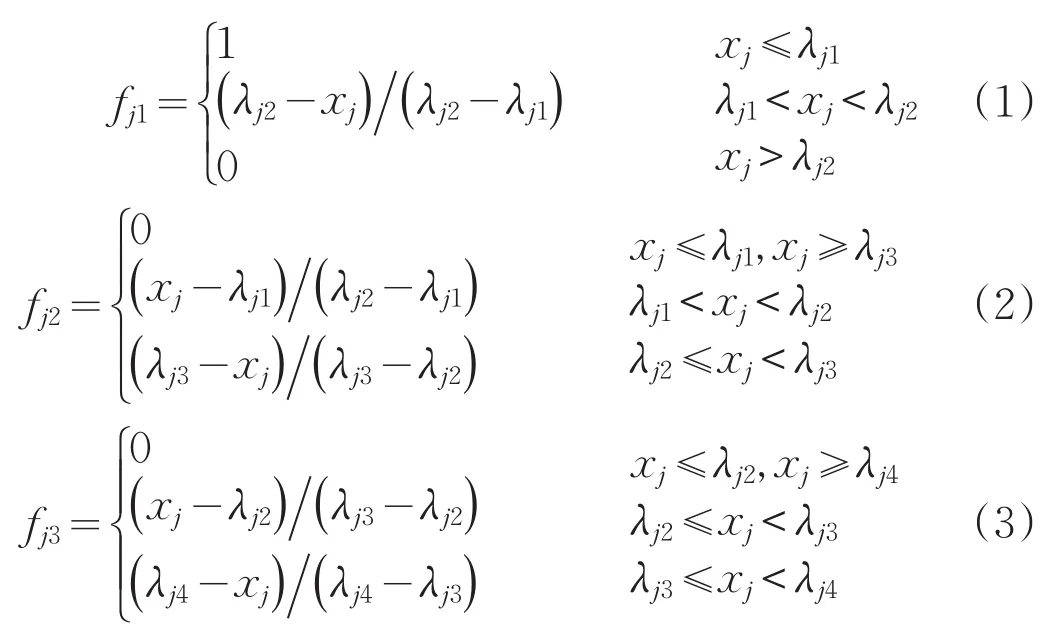
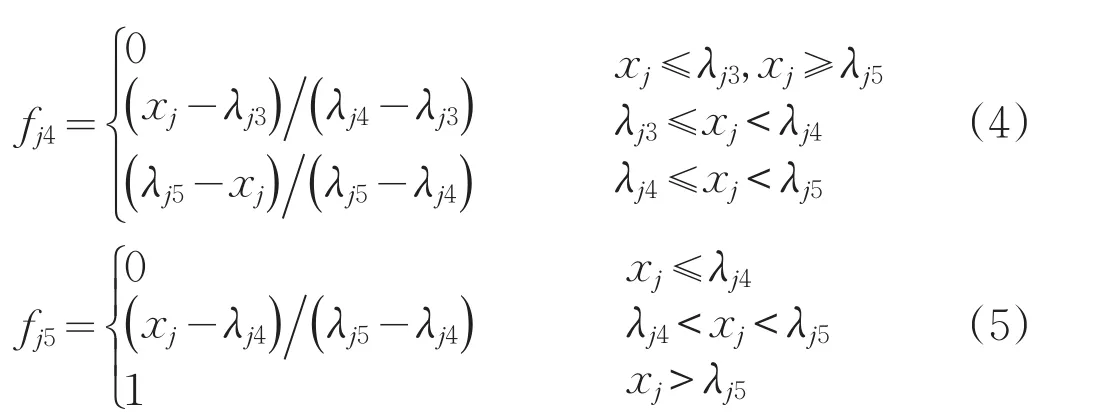
式中:fj1、fj2、…、fj5——聚类灰数(灰类)k对第j个聚类指标(评价因子)x值的白化函数;
λj1、λj2、…、λj5——第j个聚类指标(评价因子)的地下水灰类分级标准;
xj——第j个评价因子的实测含量。
3.3.2 求灰色聚类权
灰色聚类权,是以分级标准为基础求算的某评价因子对某级水的权重。评价因子(聚类指标)j对于灰类k的灰色聚类权ηjk按下式计算:
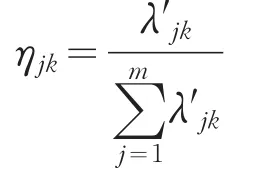
式中:λ′jk——第j个评价因子对于灰类k的分级标准的均匀化无量纲处理,λ′jk=λjk/λjb;
λjb——第j个评价因子的饮用水标准;
λjk——第j个评价因子对于聚类灰数(灰类)k的分级标准;
m——评价因子(聚类指标)个数。
3.3.3 求聚类系数及聚类
聚类系数是标定聚类对象(监测点,i=1,2,3,…,n)属于某灰类程度的系数。
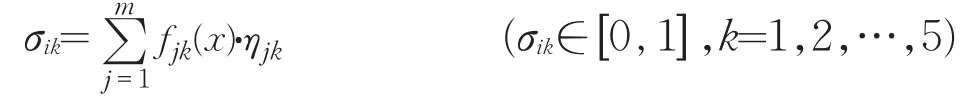
根据上式计算结果,每个监测点即形成一个以聚类系数表示的聚类行向量:σi=(σi1,σi2,…,σik),按择大原则即可确定监测井的地下水质量级别。
3.4 模糊数学综合评价法
3.4.1 数学模型
B=A·R
式中:B——由隶属度表示的水质级别模糊评价向量;
A——参加评价因子经归一化后的权重组成的行距阵;
R——各单因子评价行距阵组成的模糊关系矩阵。
3.4.2 权重行矩阵A的确定
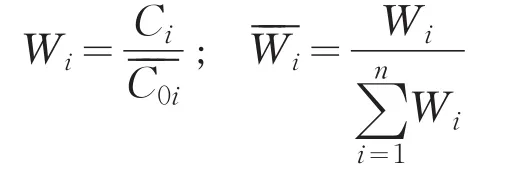
式中:Wi——i指标的权系数;
Ci——i指标实测浓度,i=1,2,…,n;
n——指标个数;
m——水质分级级数;
C0ˉij——水质为j级i指标标准浓度。
由上述指标组成一个权重行矩阵A:

3.4.3 计算隶属度,建立模糊关系矩阵
各项指标的隶属度计算同(1)~(5)公式,可得到n项指标的单因素模糊矩阵R。

3.4.4 模糊综合评价
模糊综合评价合成运算中的算子较多,本文采用〈·—max〉法进行合成运算,即以行矩阵A的元素与模糊矩阵R的各列中对应元素相乘后取最大值作为各水质级别的隶属度,据最大隶属度原则评判出水体的水质级别。
4 评价结果及简析
按以上评价步骤,选取流域内有代表性的18组地下水水质监测资料,对流域内地下水质量进行综合评价,评价结果见表4。
浓度法仅能够对某一地区的地下水质量进行粗略评价,表明评价地区地下水中的超标因子的数量及超标率,不能对评价区总体的地下水质量得出清晰的轮廓;其优点是较为直观明了,一般多用于环境水文地质条件简单,超标因子单一的地区,或者是在地下水质量评价的初期使用。
综合指数法、灰色聚类法和模糊数学综合评价法3种方法的共同之处是都可以使用相同的地下水质量级别划分标准,3种评价方法亦表现出不同的优缺点。
综合指数法全面考虑了所有评价因子的质量级别,突出单个因子的质量对整个地下水质量的影响,计算方法简单易行,评价结果直观,精确度高,信息利用率较高,缺点是地下水水质类别单项组分分值和地下水质量综合评价分级人为性较大。
灰色聚类法突出强调了地下水质“中间过渡”的灰色性,具有分辨力较强、灵敏度较高等优点。缺点是虽然全面考虑了所有评价因子的质量级别,但评价因子所属质量级别的多寡对最终地下水质量有一定的影响,有对单个评价因子质量级别综合平均的倾向,没有突出单个超标因子对整个地下水质量的制约作用。
模糊数学综合评价法具有很强的分辨力和灵敏度,能真实地反映地下水客观实际,以多个指标的隶属函数(隶属度)刻划地下水质量,既突出了单个因子的质量级别,又综合考虑了评价因子整体的质量级别。缺点是分析计算工作量较大。
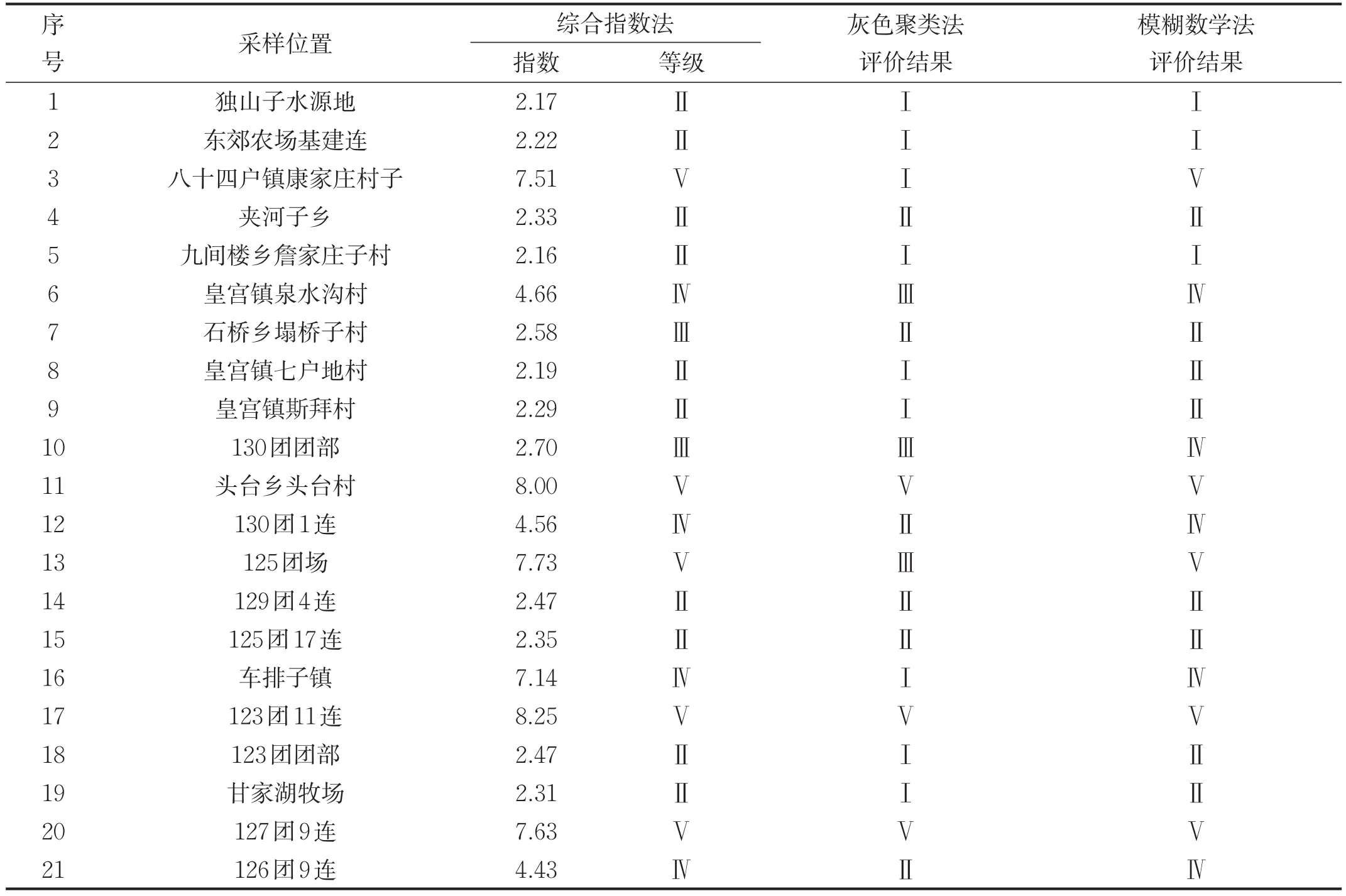
表4 流域地下水质量综合评价结果表
5 结论
奎屯河流域平原区主要开采含水层地下水质量较好,地下水质量评价结果多为Ⅰ-Ⅲ级,为完全适宜饮用的地下水。
流域内个别地段地下水已受到污染,地下水质量属Ⅳ-Ⅴ级,地下水中超标组分为矿化度、总硬度、SO42-,局部地段为NO3--N、F-、AS,流域下游125团—126团沿线地下水中F-离子含量普遍较高,部分地段地下水质量属Ⅳ-Ⅴ级。
通过使用浓度法、综合指数法、灰色聚类法和模糊数学综合评价法等方法对流域平原区地下水质量的评价及结果分析,可以看出,综合指数法和模糊数学综合评价法评价结果更符合实际。
[1]蒋辉.环境水文地质学[M].北京:中国环境科学出版社,1993.
[2]张俊福.应用模糊数学[M].北京:地质出版社,1988.
[3]潘乃礼.地下水水质现状和预测评价的理论与方法[M].北京:原子能出版社,1995.

