土中爆炸冲击作用下埋地输气管道冲击响应的数值分析
刘平,曹小康,蔡向昇,杨荣强
(中建五局土木工程有限公司,湖南长沙410004)
1 概述
南宁市邕宁区蒲津路改造二期道路等级为城市主干路Ⅰ级,路线全长约4640m;该道路位于K4+960~K4+985处有燃气管道下穿道路,燃气管道东南—西北走向,燃气管道埋深约1m。燃气管道两侧,西侧出露岩石与燃气管道最近距离约为70m(孤石开挖段为K4+760~K4+890段);东侧靠近燃气管道一侧岩石较完整,且石方量较大,开挖岩石与燃气管道最近距离约为50m。
高压燃气管道是生命线工程,一旦出现事故,后果不堪设想。因此,在燃气管道附近《爆破安全规程》(GB6722-2014)中对此也没有明确的规定。因此为了了解埋地输气管道在土中爆炸载荷下的动力响应的基本规律并对其进行安全评估,本文依据动力有限元软件LS-DYNA 3D[1]提供的强大的流固耦合功能来实现在爆炸地冲击作用下模拟埋地输气管道与土相互作用问题,并将模拟计算结果与实验结果进行了对比分析,从而为保护埋地输气管道优化爆破设计提供理论依据。
2 研究对象的本构方程
2.1 土介质本构方程
土介质模型为带失效的Soil-and-Foam模型,其应力屈服函数采用如下公式:
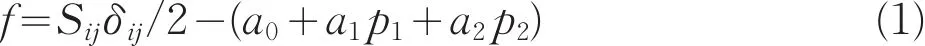
式中:Sij——偏应力张量;
δij——kronecker符号;
a0、a1、a2——常数;
p——压力,MPa。
在文献[2-4]基础上得到压力与体积应变的曲线关系和土体的物理力学参数,分别见图1和表1。
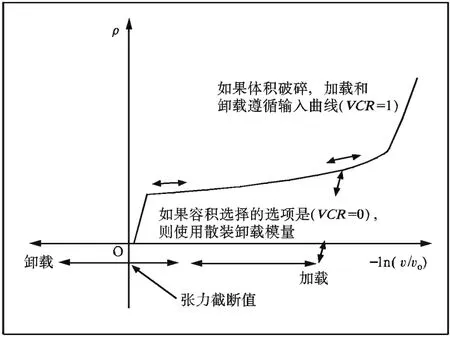
图1 Soil-and-Foam本构模型的体积应变—压力曲线
2.2 管材本构方程
埋地管线材料采用弹性—均匀塑性型材料,其本构方程采用随动硬化双线性弹塑模型,遵从Von-Mis⁃es屈服准则,其公式如下:


表1 土体的物理力学参数

式中:σ——应力;
E0——弹性模量;
ETAN——切线模量且0<Etan<E0;
σe——屈服应力;
εe——弹性极限应变,无因次;
ε——应变,无因次。
根据文献[5-6]所述,埋地钢管的物理力学参数取值如表2所示。
2.3 炸药爆轰产物状态方程

表2 埋地管线物理力学参数值
为了能够模拟土介质中的近地表爆炸过程的物理现象,在炸药爆轰问题数值计算中,采用高能炸药(TNT)燃烧函数因子模型,其爆轰产物状态方程采用JWL状态方程:
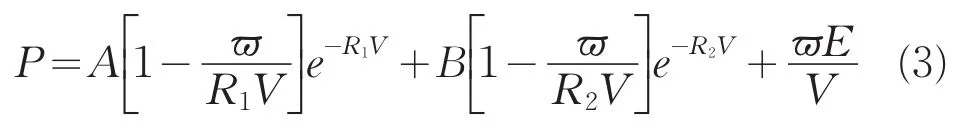
式中:P——爆炸产生压力;
V——相对体积;
E——炸药比内能;
A、B、R1、R2、ω——实验确定的参数。
TNT炸药的材料模型参数[7-8]如表3所示。
3 物理力学模型

表3 TNT炸药的材料模型参数值
3.1 物理力学模型
根据莱斯默提出的无反射边界条件,设定土体模型左右前后四侧面和下部均为非反射边界,顶部为自由边界,故图2所研究的力学物理模型属于半无限土介质中爆炸作用问题。炸药以圆柱形装药形式埋在土块当中,埋地管道覆土深度为H,装药点到管道的中心距离为R,选取直径0.2m的TNT炸药,密度为1.2g/cm3;埋地管道的外径为0.15m,壁厚为0.02m。
3.2 有限元网格划分
图2坐标系中水平方向x轴,垂直方向为y,垂直纸面向里为z轴(即与管道轴向平行方向),图2所示的力学物理模型为轴对称装药,为了节省求解时间,可取力学物理模型的1/2部分进行计算。采用Lagrange单元来模拟管道,采用Eulerian单元来模拟土体和炸药,两者之间的相互作用以流固耦合方式进行分析且每个方向上都要进行耦合分析;埋地管道和土壤之间的相互作用采用面面接触分析。炸药、土壤和管道分别选择SOLID164六面体单元进行网格划分。
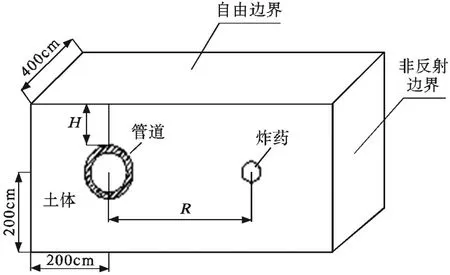
图2 力学物理模型
4 数值模拟结果与分析
为了清楚地了解在不同装药量和爆心距的条件下管道表面在爆炸冲击荷载的响应规律,现分析以下2种情况共10种工况,如表4所示。
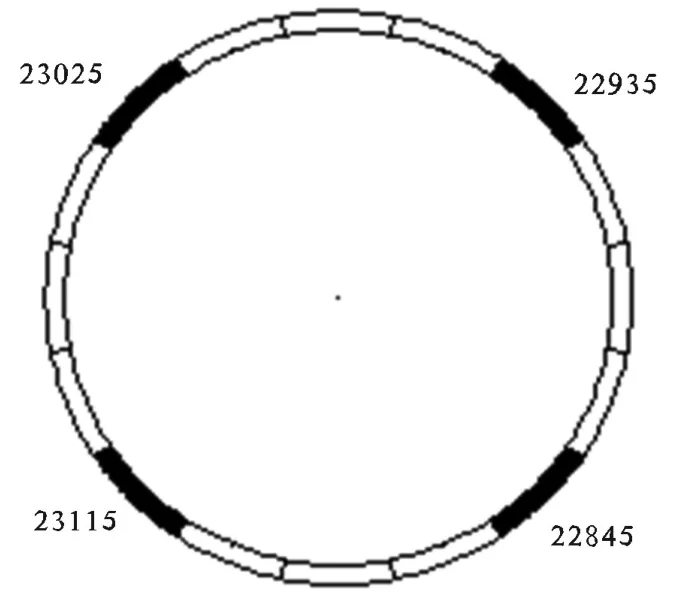
图3 单元位置图

表4 计算工况
4.1 质点最大振速与装药量和爆心距离的关系
工程中,通常采用萨道夫斯基经验公式来计算爆破质点峰值振速采用式(4)计算,参数参照《爆破安全规程》(GB6722-2014)(10-11)选取:

式中:V——计算的振动速度,cm/s;
R——爆源至被保护对象的距离,m;
Q——炸药量,齐发爆破为总药量,延时爆破为最大一段药量,kg;
K、∂——与爆破点至被保护对象间的地形、地质条件有关的系数和衰减指数。
4.2 分析结果
根据文献[9]可知,随着时间的推移,土体中的炸药产生的应力波作用到管道表面,由于管道的受力是瞬态过程的,故正对爆心的管道迎爆面上的应力最大。本文选取正对爆心的管道横截面上的4个微元作为研究对象,微元位置如图3所示;图4所示为第1组第3种工况下的速度时程图。从图4中可知,单元22935所在的位置即为管道迎爆面上速度响应的峰值,埋地管道振动速度在t=15ms时达到最大,故定义此时单元22935的振动速度为管道质点的峰值振速,在其余9种工况下管道的应力时程变化规律是类似的。

图4 单元速度时程图
通过表4中第1组工况对应的数值模拟结果来计算装药量与管道的质点最大振动速度之间的关系。装药量1、3、5、7、9kg对应的管道质点最大振速分别为0.28465、0.48745、0.69436、0.82354、0.91457m/s,绘制成装药量与管道的质点最大振动速度的曲线并对其进行最小二乘拟合,获得质点最大振动速度与装药量之间的关系为:
Vmax=0.1734W0.6875(5)
因此,通过公式(4)和公式(5)可得,爆破点场地条件有关的系数为206.25,衰减系数为2.3452。

图5 管道最大速度响应与装药量的关系曲线
在第2组工况下,由公式(4)、(5)可得到质点最大振速与管道中心距离和爆心之间的关系为:

在第2组工况下,分别对应管道中心距离和爆心3.0、4.0、5.0、6.0、7.0m时,通过数值模拟计算得出管道质点最大振速分别为0.68745、0.30256、0.18742、0.14235、0.13024m/s,如图5所示。结果表明:数值计算结果与经验计算结果十分吻合,证实了数值模拟结果描述了在爆炸荷载作用下埋地输气管道动态响应过程中的合理性。
5 结论
基于ALE算法进行数值模拟的结果分析可得,在爆炸作用下,为了保证埋地管道的安全运行和施工进度,故在爆破时必须严格控制最大一次起爆药量和爆心至管道之间距离。同时文中将经验公式规律计算的结果与数值模拟计算结果进行比对,证实了数值模拟结果的合理性,说明运用非线性动力学基本理论和ALE算法可以很好地分析在临近埋地管道的土中爆破荷载下的动态响应,这将为埋地输气管道在第三方荷载作用下的风险评估提供了一个有效方法。
[1]LS-DYNA Structured User′s Manual[M].Liver More Software Technology Corp,1999.
[2]廖维张,杜修力,田志敏.爆炸荷载作用下部分埋置结构响应的数值模拟方法[J].北京工业大学学报,2007,33(2):155-159.
[3]Wang Qing-jie.Investigation of Blast Effection of Experiment and Numerical Simulation for Group Charging Multilayer Medi⁃um[D].Nanjing:PLA Engineering Institute of Engineering Corps,1996.
[4]Experimental Report on Loessial Cutting Lines[R].89002Unit,PLA,1983.
[5]贾普荣,李年,朱维斗.反向加载时X70钢的力学性能[J].机械强度,2005,27(1):82-84.
[6]杨政,郭万林,董惠茹,等.X 70管线钢静态和动态韧性试验研究[J].西安交通大学学报,2003,37(5):488-491.
[7]Zhang Guan-ren.Agglomeration Dynamite Explosion Dynam⁃ics[M].Beijing:National Defense and Industry Publishing Com⁃pany,1991.
[8]钱七虎,王明洋,赵跃堂.三相饱和水土中爆炸波在障碍物上的反射荷载[J].爆炸与冲击,1994,14(3):97-104.
[9]都的箭,刘志杰,马书广.埋地管线在爆炸地冲击作用下的数值模拟[J].地下空间与工程学报,2007(2):181-186.
[10]袁良远,唐春海,朱加雄,白玉.高速公路隧道下穿既有铁路隧道控制爆破技术[J].工程爆破,2016,22(1):64-67.

