基于 D-S 证据理论的城市轨道交通线网规划评价研究

石红国，贺玉姣

SHI Hong-guo, HE Yu-jiao

（西南交通大学 交通运输与物流学院，四川 成都 610031）

(School of Transportation and Logistics，Southwest Jiaotong University， Chengdu 610031， Sichuan， China)

目前我国大部分大中型城市均面临交通拥堵问题，城市轨道交通因其高效、安全、环保等特点，已经成为解决大型城市交通拥堵问题的首要选择[1]。城市轨道交通线网规划评价贯穿于线网方案设计及优化决策的始终，作为轨道交通规划的关键环节之一，直接决定着城市轨道交通线网规划的优劣，深刻影响到整个城市轨道交通系统的成败。为了对城市轨道交通线网规划进行科学评价，许多学者提出多种定性和定量的分析评价方法，如牟浩[2]提出城市轨道交通网络规划决策的物元熵权评价模型，并对长沙市城市轨道交通线网规划进行实证分析；王念念[3]通过模糊层次分析法确定评价指标体系的权重，提出基于灰色最大关联度法的城市轨道交通规划线网评价模型，并对无锡市轨道交通线网规划进行评价。此外，专家学者还对城市轨道交通在效能、综合效益、路网运营安全等方面的评价进行研究[4-6]。在大多数定量评价中，评价目标的分数数值通常采用专家打分的方法，而城市轨道交通线网规划的指标体系具有模糊性和不确定性，专家打分往往与自身经历和经验有关，会呈现出随机性和不确定性。因此，引入 D-S 证据理论，将不确定结果进行可靠的数值转换，将多个证据进行融合，从而实现较可靠地评价城市轨道交通线网规划[7]。

1 D-S 证据理论的原理

1.1 基本原理

证据理论是贝叶斯概率的推广，能够以不确定信息为基础进行可信度推理，由 Dempster 于 1967年首先提出，并由 Shafer 于1976年进一步发展起来的一种不精确推理理论，也称为 Dempster/Shafer 证据理论 (D-S 证据理论)。证据理论的主要特点是满足比贝叶斯概率更弱的条件，具有直接表达“不确定”和“不知道”的能力。该方法已经成功应用于建筑火灾安全评价、作业人员安全行为评价、海军系统安全分析与综合、软件需求评价等方面[8-10]。城市轨道交通线网规划是一个较为宏观的评价对象，许多评价因素具有模糊性、随机性和不确定性，不同专家对同一因素的评价结果可能会存在较大差异。因此，应将不同专家的评价结果合理地融合起来，方能较精确地评价城市轨道交通的线网规划。

1.2 评价信息的表达

对于证据理论，评价中的证据可用一个有限集合 θ = {A1，A2，…，An} 表示，若 θ 非空，则 θ 即为评价的识别框架[11]。给定识别框架 θ，则基本信度分配函数 M 是一个集合 2θ→[0，1] 的映射，A 为识别框架中的任一子集，且满足公式⑴，则称 M (A)为基本概率赋值，其中 2θ为 θ 的幂集。

式中：φ 为空集。

对于给定的 M，对任意 A ∈ 2θ定义相应的信任函数和似然函数见公式 ⑵ 和公式 ⑶。

式中：信任函数 Bel (A) 为对 A 的总信任，是支持A 的最小值；似然函数 Pl (A) 为不否定 A 的信任度，是支持 A 的最大值。这样 [Bel (A)，Pl (A)] 就自然形成对 A 的信任区间 (容易证明得到不等式 Pl (A)≥Bel (A)，而 Pl (A)－Bel (A) 则用来表示不知道 A 的程度。

1.3 评价结果的信息融合

采用 Dempster 合成规则合成评价指标的基本概率赋值，进行正交和运算。

设 M1和 M2是2个基本概率赋值，则其正交和M = M1⊕M2，其证据融合规则为

同理，对于有限 n 个基本概率赋值 M1，M2，…，Mn，则其正交和 M = M1⊕M2⊕…⊕Mn，其证据融合规则为

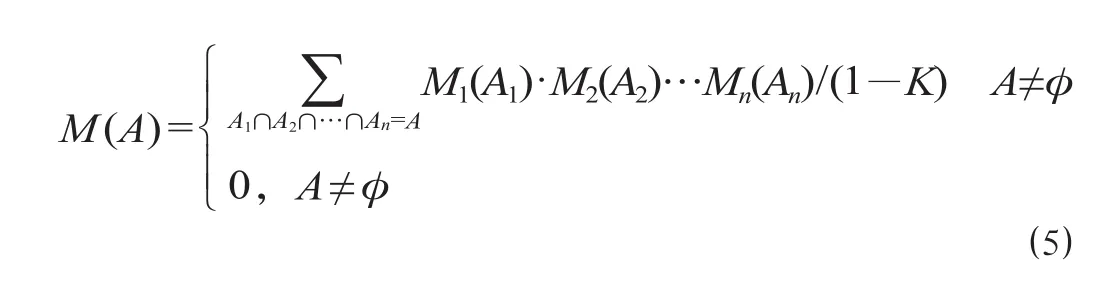
2 基于证据理论的城市轨道交通线网规划评价步骤

城市轨道交通线网规划的总体目标是协调好交通需求与供给之间的关系、实现城市土地规划发展目标、实现交通战略目标。为评价城市轨道交通线网规划，首先需要构建科学的评价指标体系，由于大部分评价指标的权重难以量化，因而通过层次分析法 (AHP) 确定每种因素的权重，接着通过多名专家对每种因素的打分获得证据，从而确定每个指标的综合概率值，最后对证据进行融合处理，得出评价结果。具体地，基于证据理论的城市轨道交通线网规划评价基本步骤如下。

（1）建立城市轨道交通线网规划评价指标体系。通过查阅相关资料，对多个城市的轨道交通线网规划评价指标体系进行比较分析，结合本地实际情况，尽可能合理地建立适用于本地的评价指标体系。

（2）确定各级指标的权重。采用 AHP 法，通过专家打分，构建判断矩阵，得到排序权向量，计算判断矩阵最大特征值，进行一致性检验，最终确定指标体系中的各个因素权重值，各级权重值总和为1[12]。

（3）评价因素概率赋值。专家组成员对评价因素进行打分，分值的上界为 1，下界为 0。分值越趋近于 0，表明该评价因素本身的状态越达不到理想的目标，分值越接近于 1，表明该评价因素本身的状态越接近理想目标。这种打分制既可以避免打分的简单单一性，又提高专家评分的灵活度，因而更接近于现实情况。

（4）指标综合概率值的确定。对于每个评价因素，其综合概率值为专家评价概率值乘上其占总目标的权重值。以3层权重的第一个因素 θ11为例进行说明。式中：a11为专家对 θ11的评价值；q1为第二层目标的第一个因素占第一层目标的权重值；q11为第三层目标的第一个因素占第二层目标第一个因素的权重值。

由此可以获得综合概率值集合M{M {θ11}，M{θ12}，…，M {θij}}(i = 1，2，…，∞，j = 1，2，…，∞)，以及与其对应的不确定值 m {θ}= 1－M {θ11}－M {θ12}－…－M {θij}。其中，m {θ}是评价因素的概率值的补集，表达对应的不确定性。

（5）综合评价。根据每个因素的综合概率值的确定，利用公式 ⑵ 和公式 ⑶ 可以求得各大类指标信任函数的上、下界。如果有多个专家进行评价，得到多组评价结果，则可以利用公式 ⑷ 和公式 ⑸，对多组评价结果进行融合，最终得到更精确和真实的评价结果。

3 实例分析

成都地铁1号线一期工程于2005年12月开始建设，并于2010年9月投入运营。截至2017年 12月，成都地铁共开通6条线路，分别为1号线、2 号线、3 号线、4 号线、7 号线和10号线，线路总长180 km，共计120多座车站 (换乘站不重复计算)；成都地铁在建线路数量达到10条、在建里程达到335.96 km[13]。目前，成都地铁已经规划了包括 46条线路、长达 2450.04 km 的轨道交通网络，覆盖全市各个区域，并且辐射周边县市区。

3.1 评价指标体系

城市轨道交通线网规划是一个较为宏观的评价对象，既有定量指标，又有定性指标，具有不确定性、随机性和模糊性，要对其进行科学有效的评价，应当建立一套能够体现城市轨道交通线网规划特征的评价指标体系，评价指标应便于对线网在空间上和时间上进行综合比较[14]。目前我国上海、北京、广州、南京等城市在轨道交通线网规划的工作中，根据自身城市特点对线网进行了综合评价，但各城市所确定的指标体系准则层不一，从而对决定轨道交通线网方案主导因素的反映有所不同[15]。

根据成都市自身特点，结合其他城市的评价指标体系，从线网结构、运营效果、城市协调与可持续性、社会效果和建设实施性等方面进行研究，建立了成都地铁线网规划评价指标体系。此外，通过专家打分制、层次分析法，确定了指标中的各因素权重。成都地铁线网规划评价指标体系及权重如表1 所示。

表1 成都地铁线网规划评价指标体系及权重Tab.1 Evaluation index system and weight of Chengdu Metro network planning

3.2 初级评价

3.2.1 评价初始数据

根据表1中的成都地铁线网规划评价指标体系，得到评价因素集合为 θ = {θ11，θ12，θ13，θ14，θ15，θ21，θ22，θ23，θ24，θ25，θ31，θ32，θ33，θ34，θ41，θ42，θ51，θ52，θ53，θ54}。

专家组成员对指标体系内的评价因素进行打分，分值越趋近于 0，表明该评价项目离目标期望值越远，需要大幅度改进。分值越接近于 1，表明该评价项目离目标期望值越接近，完成度越好。成都地铁线网规划评价结果分类如表2所示。

针对表1所建立的评价指标体系，不同专家打分结果汇总如表3所示。

表2 成都地铁线网规划评价结果分类Tab.2 Chengdu Metro network planning assessment results and classification

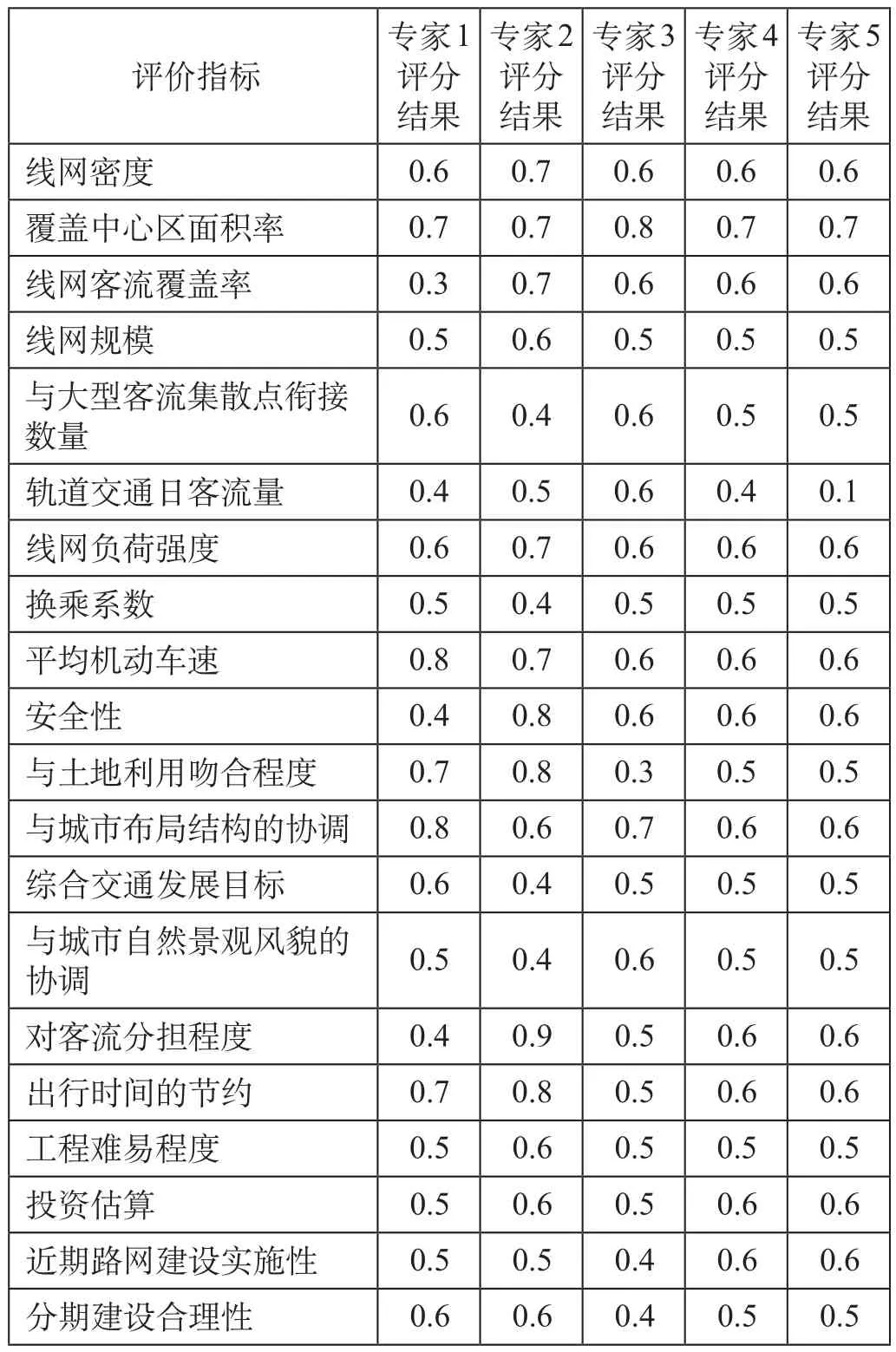
表3 成都地铁线网规划专家评分汇总表Tab.3 Expert rating summary of Chengdu Metro network planning

3.2.2 指标综合概率值

根据每个评价因素所在层次，评价因素的概率值为评价分值对应总目标的综合权重，综合权重与评价结果数值相乘即为综合概率值。以因素“线网密度”为例，对于专家1来说，该因素的综合概率值为 M {θ11}= a11×q1×q11= 0.29×0.2×0.6 = 0.0348。依此类推，可以得到综合概率值集合 M {M {θ11}，M {θ12}，…，M {θ54}}，以及其对应的不确定性值m {θ} = 1－M {θ11}－M {θ12}－…－M {θ54}}。

3.2.3 评价分析

由表3可知，共有5位专家对评价因素进行打分，分值越趋近于 0，表明该评价项目离目标期望值越远，需要大幅度改进。分值越接近于 1，表明该评价项目离目标期望值越接近，完成度越好。

利用综合概率值计算可得第一位专家评价的综合概率值集合为 M {M {θ11}，M {θ12}，…，M {θ54}，m {θ}}= {0.0348，0.0294，0.0126，0.0120，0.0204，0.0184，0.0228，0.0110，0.0256，0.0248，0.0280，0.0464，0.0408，0.0170，0.0400，0.0700，0.0490，0.0180，0.0200，0.0156，0.4434}。

在此基础之上，利用公式 ⑵ 可以得到线网结构 θ1的信任函数

类似地，Bel (θ2) = 0.1026，Bel (θ3) = 0.1322，Bel (θ4) = 0.1100，Bel (θ5) = 0.1026。

利用公式 ⑶ 可以得到线网结构 θ1的似然函数

类似地，有 Pl (θ2) = 0.5460，Pl (θ3) = 0.5756，Pl (θ4) = 0.5534，Pl (θ5) = 0.5460。

可见，由线网结构 θ1引起的线网规划评价的赋值下界为 0.1092，上界为 0.5526。其余评价指标的上、下界依此类推。对于不确定性问题，与利用其他评价方法相比，运用证据理论可以将不确定性概率的范围确定，从而便于对该问题的进一步量化分析。

3.3 证据融合

证据融合是证据理论优势的最重要体现，特别是当不同的专家给出的评价结果存在差异时，依据证据理论依然可以得到较可靠的评价结果。从表 3可以发现，对于有些评价指标，不同专家给出的评分数值差别较大。因此，进行数据融合十分必要。

根据前述可以得到专家1的信任函数集合如下。0.4434}

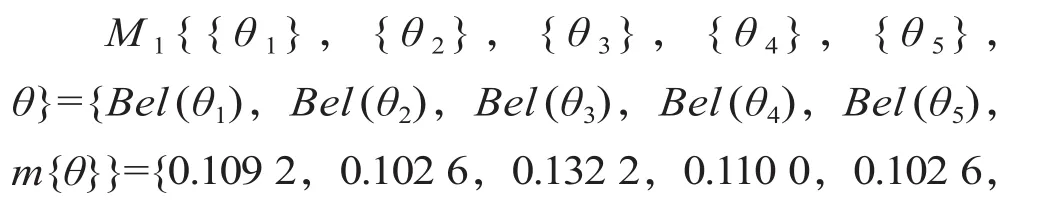
类似地，可以得到其他专家的信任函数集，5位专家对每个评价指标的信任函数值如表4所示。

将专家1和专家2的评价数值进行融合，根据公式 ⑷ 和公式 ⑸ 进行正交和运算如下。

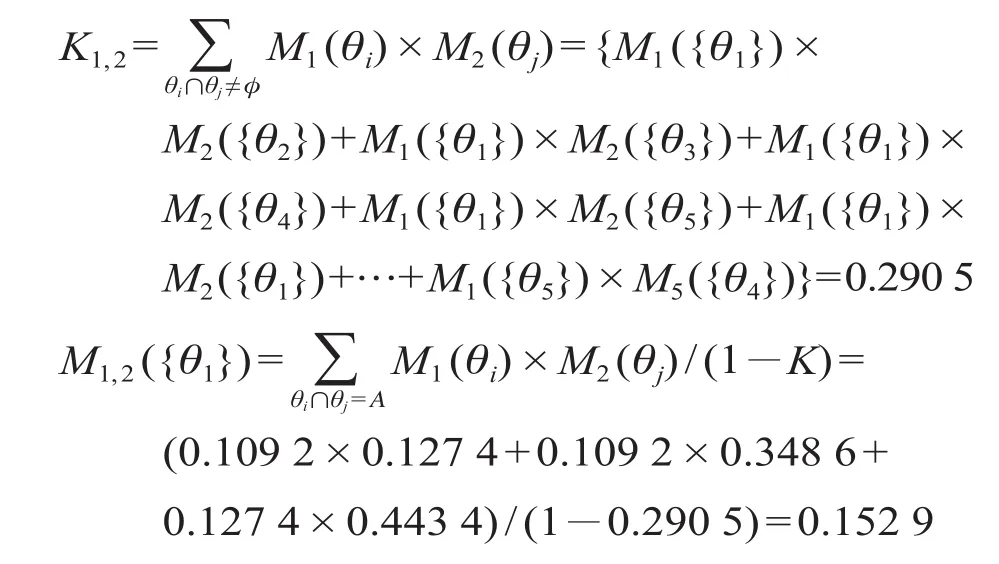
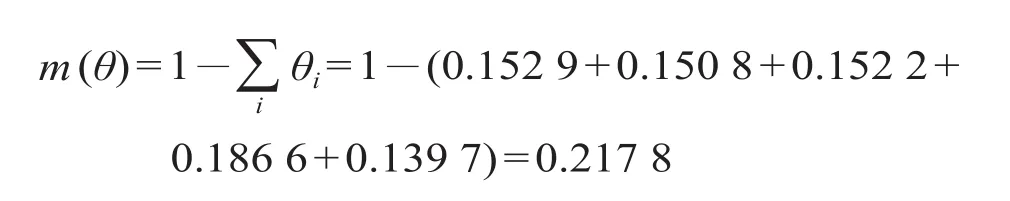
整理可得

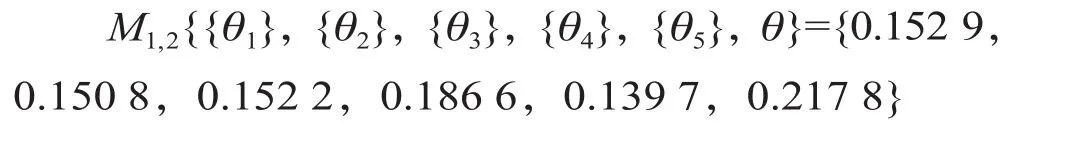
再将以上结果与其他专家的评分结果逐个融合，得到融合结果如表5所示。

同理

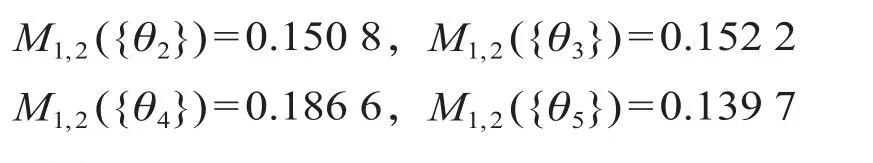
则有

表4 专家组评价信任函数值表Tab.4 Trust function value of expert group evaluation

至此，由表4可以发现，1 至5号专家的评分结果分别都为“较好”，即成都地铁线网规划能较好地达到理想目标。由表5可以发现，5 位专家评分结果融合后的结果为 Bel ({θ1，θ2，θ3，θ4，θ5}) = 1－m (θ) = 1－0.0794 = 0.9206，Pl ({θ1，θ2，θ3，θ4，θ5}) = 1，信任区间为 [0.9206，1]，不确定度为 0.0794。因此，综合评定结果为“好”，即与理想目标十分接近。

可以发现，1 至5号专家每个专家的评价结果中总会有几个评价结果数值偏低，而对5个专家的数据进行融合之后，可以发现，对于意见较一致的评价结果数值，会发生加强的作用，而对于意见有冲突或较为不一致时，会综合考虑相同的部分，进行合理地融合。

此外，设置了对比组，4 号专家和5号专家对3 层指标“轨道交通日客流量”的评价结果数值不一样，4 号专家评价结果为 0.4，5 号专家评价结果为 0.1，其他指标评价结果都一样，分别对1号、2 号、3 号、4 号专家 (简称 (1) 组) 和1号、2 号、3 号、5 号专家 (简称 (2) 组) 的评价结果进行融合，得到结果如表6所示。

即 (1) 组融合后的结果为 Bel ({θ1，θ2，θ3，θ4，θ5}) = 0.8931，Pl ({θ1，θ2，θ3，θ4，θ5}) = 1，(2) 组融合后的结果为 Bel ({θ1，θ2，θ3，θ4，θ5}) = 0.8914，Pl ({θ1，θ2，θ3，θ4，θ5}) = 1。由此可以发现，(2) 组比 (1) 组的信任函数降低了 0.0017，不确定性有所增加，这是由于专家5的评价结果与前3位专家的评价结果相差较大，因而不确定性增加。

通过以上分析可以发现，证据理论可以有效地融合证据 (即评分) 中的一致部分，对一致部分会进行结果的加强，从而会减小数据中不确定性值的范围，使评价结果更加精确可靠；在有数据冲突或较为不一致时，该方法也综合考虑各证据之间的共同部分，进行合理地融合，避免因人的判断误差而对最终结果产生影响。

4 结束语

通过建立城市轨道交通网络规划评价指标体系，利用 AHP 方法确定权重，运用 D-S 证据理论，对多组评价结果进行合理融合，设置对照组，验证证据理论可以有效地减少因人的判断偏差而引起的随机误差。对成都市城市轨道交通线网规划评价结果显示，对于一致的评价结果，证据理论的融合法则能够有效地将不确定范围减少；对于存在一定冲突的评价结果，通过证据理论的融合法则处理，最终结果能综合其一致部分，进行有效的融合。此外，成都市城市轨道交通线网规划案例表明，社会效果的好坏对整个体系影响较大，在城市轨道交通网络规划中，应着重注意城市轨道交通对社会的影响效果。

表5 融合结果Tab.5 Fusion results

表6 对照组融合结果表Tab.6 Fusion results of control group

[1] 黎 林，王晋强，田 钊，等. 城市地铁商铺租金定价方法的研究[J]. 铁道运输与经济，2017，39(2)：16-17.LI Lin，WANG Jin-qiang，TIAN Zhao，et al. Study on Rent Pricing Method of Commercial Premises in City Metro[J].Railway Transport and Economy，2017，39(2)：16-17.

[2] 牟 浩. 城市轨道交通网络规划综合评价研究[D]. 大连：大连理工大学，2014.MOU Hao. Comprehensive Evaluation Research of City Rail Transit Network Planning[D]. Dalian：Dalian University of Technology，2014.

[3] 王念念. 城市轨道交通规划线网综合评价研究[D]. 北京：北京交通大学，2007.WANG Nian-nian. Study on Comprehensive Evaluation of Urban Rail Transit Network Planning[D]. Beijing：Beijing Jiaotong University，2007.

[4] 胡 松. 城市轨道交通效能评价研究[D]. 北京：北京交通大学，2015.HU Song. Effectiveness Evaluation of Urban Rail Transit[D].Beijing：Beijing Jiaotong University，2015.

[5] 穆 辉. 城市轨道交通的综合效益评价[D]. 成都：西南交通大学，2007.MU Hui. Comprehensive Benefit Evaluation of Urban Rail Transit[D]. Chengdu：Southwest Jiaotong University，2007.

[6] 黄雅坤. 城市轨道交通路网运营安全评价方法研究[D]. 北京：北京交通大学，2014.HUANG Ya-kun. Research on Evaluation Method of Urban Rail Transit Network Operational Safety[D]. Beijing：Beijing Jiaotong University，2014.

[7] 马 剑，叶 新，林 鹏. 基于证据理论的地铁火灾安全评价方法[J]. 中国安全生产科学技术，2017，13(1)：134-139.MA Jian，YE Xin，LIN Peng. Safety Evaluation Method of Subway Fire based on Evidence Theory[J]. Journal of Safety Science and Technology，2017，13(1)：134-139.

[8] 王 晨. D-S 证据理论在商场或在安全评价中的作用[J]. 消防科学与技术，2010，29(4)：335-338.WANG Chen. Application of D-S Evidence Theory in Shopping Center Fire Safety Assessment[J]. Security and Safety Technology Magazine，2010，29(4)：335-338.

[9] 郑霞忠，石法起，陈 述，等. 基于 D-S 证据理论的地下洞室作业人员安全行为评价[J]. 中国安全生产科学技术，2016，12(6)：158-161.ZHENG Xia-zhong，SHI Fa-qi，CHEN Shu，et al.Evaluation on Safety Behavior of Workers in Underground Cavern based on D-SEvidence Theory[J]. Journal of Safety Science and Technology，2016，12(6)：158-161.

[10] 孙越林，包 磊. 基于 D-S 证据理论的海战场目标战术意图识别技术研究[J]. 舰船电子工程，2012，32(5)：48-51.SUN Yue-lin，BAO Lei. Study on Recognition Technique of Targets’ Tactical Intentions in Sea Battlefield based on D-S Evidence Theory[J]. Ship Electronic Engineering，2012，32(5)：48-51.

[11] SHAFER G. A Mathematical Theory of Evidence[M]. New Jersey：Princeton University Press，1976.

[12] 黄 凯，李晟东. 基于 AHP 和粗糙集的危险货物集装箱多式联运安全综合评价[J]. 物流技术，2016，35(10)：74-77.HUANG Kai，LI Sheng-dong. Comprehensive Safety Evaluation of Containerized Inter-modal Transportation of Hazardous Cargo based on AHP and Rough Set[J]. Logistics Technology，2016，35(10)：74-77.

[13] 成都地铁[EB/OL]. (2017-12-15)[2017-12-17]. https∶//baike.baidu.com/item/%E6%88%90%E9%83%BD%E5%9C%B0%E9%93%81/1025483?fr=aladdin,2017-4-9.

[14] 葛 芳. 基于证据理论和突变理论的大城市公交线网综合评价研究[J]. 交通运输系统工程与信息，2009，9(5)：171-174.GE Fang. Overall Evaluation and Study on Public Transport Network in Large Cities based on Dempster-Shafer Theory and Catastrophe Theory[J]. Journal of Transportation Systems Engineering and Information Technology，2009，9(5)：171-174.

[15] 孙文桥，刘启刚，凌 熙，等. 铁路物流中心设计方案仿真评估优化技术研究[J]. 铁道货运，2017，35(9)：1-2.SUN Wen-qiao，LIU Qi-gang，LING Xi，et al. Study on Optimization Technology of Simulation and Evaluation of Railway Logistics Center Design Program[J]. Railway Freight Transport，2017，35(9)：1-2.