不同限速下基于随机森林的列车区间运行时分预测研究
周晓昭,张 琦,许 伟
ZHOU Xiao-zhao1, ZHANG Qi2, XU Wei2
(1.中国铁道科学研究院 研究生部,北京 100081;2.中国铁道科学研究院 通信信号研究所, 北京 100081)
(1.Department of Graduate Programs, China Academy of Railway Sciences, Beijing 100081, China 2.Signal &Communication Research Institute, China Academy of Railway Sciences, Beijing 100081, China)
0 引言
正常条件下,列车在区间运行时分几乎不变,但遇到因大风、降雨、降雪等天气,以及线路、设备故障时,为保证列车运行安全,一般会设置限速。由于限速,列车不能按原计划速度运行,必然会导致区间运行时间增加,进而导致列车晚点及后续列车的连带晚点。当列车偏离基本运行图运行时,目前调度员凭经验预估区间限速后列车在区间的运行时分来重新调整运行图,这种凭借人工经验的方式不具备可靠性,无法及时、合理、有效地安排行车。随机森林算法是利用多个弱分类器结合成一个强分类器的分类算法,具有并行计算、训练速度快,不易出现过拟合,构建模型预测准确度高等优点。国内外学者针对随机森林算法的应用已做过一些研究,如 Ham 等[1]将随机森林算法应用于高光谱数据的分类,El-Manzalawy 等[2]用随机森林算法预测保护细菌抗原,Bellos 等[3]将随机森林算法应用于慢行阻塞性肺病患者的健康状况分类研究,丁君美等[4]将随机森林算法应用于预测电信业客户流失,袁志明等[5]将随机森林算法应用于预测列车的到站时间,齐雁冰等[6]将随机森林算法应用于预测土壤有机质空间。随机森林算法已经成功应用于医疗、生物、科技、化工、交通等很多领域。因此,研究采用随机森林算法对大量的时空历史列车运行数据进行分析,挖掘隐藏在大量时空历史列车运行数据背后的规律,预测不同限速条件下列车在不同区间的运行时分。
1 随机森林算法原理
随机森林是以决策树为基学习器的集成学习Bagging 的一种实际应用算法。集成学习的核心是构建多个不同的模型,通过组合多个基学习器来获取比单个基学习器显著优越的泛化性能。集成学习方法有并行方法和顺序方法2种。随机森林属于并行方法,在决策树的训练过程中引入随机属性选择,有效地降低各个基学习器的相关度。随机森林是利用自助采样法从原始数据样本中随机且有放回地抽取多个与原始样本相同容量大小的样本集[7],并对每个样本集单独构建决策树,然后根据每棵树给出的结果,通过投票或取平均值的方式得出最终的预测结果。
随机森林算法原理图如图1所示。
从数据集 DataSet 中随机且有放回地抽取m个与原始样本相同容量大小的样本集,通过 m 次训练,得到 m 棵不同的决策树{h (X,θi),i = 1,2,…,m},其中 X 为训练子集,θi为第 i 棵决策树具有独立同分布的随机向量,h (X,θi) 为决策树;再将m棵树组合成一个组合分类模型,并采用简单多数投票法得出该模型的最终分类结果,可以表示为最后分类结果,hi(X)为单棵决策树的分类结果,Y为类别标签,I(·) 为示性函数。

图1 随机森林算法原理图Fig.1 Principle map of random forests
给定包含 个样本的训练数据集,先从数据集 D中随机取出1个样本放入采样集 DS中,再把该样本放回 D 中(有放回的重复独立采样)。经过 N 次随机采样操作,得到包含m个样本的采样集 DS。数据集 D 中可能有的样本在采样集 DS中多次出现,但 D 中也可能有样本在DS中从未出现。一个样本始终不在采样集中出现的概率是根据因而 D 中约有 63.2% 的样本出现在 DS中,约有36.8% 的样本不会出现在 DS中。这些数据就成为各个训练数据子集的 Out-ofbag (OOB) 数据。这部分数据可用来评价随机森林的分类性能,可以用来估计随机森林中各分类数的强度、分类树之间的相关度和随机森林的泛化误差。
在随机森林算法中,有2种方法可以用来确定每个变量的重要性:一是利用决策树的性质来计算变量的重要性;二是利用OOB样本来估计变量的重要性。

设 h (Xi,θi) 为由 Xi训练得到的第 i 个决策树分类器。分类器 h (Xi,θi) 对应的 OOB 数据集为 OOBi。随机森林的强度 s 是随机森林边缘函数的期望,计算公式为式中:mr (X,Y) 为边缘函数;EX,Ymr (X,Y) 为边缘函数的期望;Q (xi,yi) 为对输入的随机变量 k 在OOBi中投票的分类类别为 yi的比例;N为分类类别错误的最大概率; 为决策树的个数,i ∈ (1,2,…,N)。
随机森林的相关度 ρ—是边缘函数的方差除以标准差的平方,计算公式为
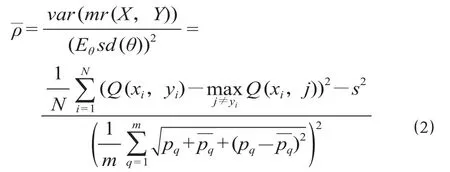
式中:var (mr (X,Y)) 为边缘函数的方差;Eθsd (θ)为标准差;s 为随机森林的强度;pq为分类正确的比值,为分类错误的比值
随机森林的泛化误差[8]PE* 计算公式为

式中:ρ—为随机森林的相关度。
2 不同限速条件下基于随机森林的区间运行时分预测模型
2.1 区间运行时分及其预测的特征属性概述
列车区间运行时分[9]在运输组织上指列车在 2个相邻车站或线路所之间的运行时间标准,由机务部门采用牵引计算和实际试验相结合的方法确定。列车区间运行时分按车站中心线或线路所通过信号机之间的距离计算。当到发场中心线与车站中心线不一致时,按到发场中心线计算。对于运行图来说,区间运行时分指列车运行线当前节点的到达时刻与上一节点的出发时刻的差值。影响列车区间运行时分的因素有区间的长度、坡度、列车车型、列车等级、列车重量、列车的运行方向、区间始端站和终端站的通过/到开标志、列车运行所在线路[10]、是否反向行车、天气情况、是否限速、限速值、限速范围、限速时间、同线路上相邻前车的速度和位置、车站到发线使用等的车站约束条件和区间约束条件等。这些影响因素将作为不同限速条件下区间运行时分预测的特征属性。
对行车数据进行深度挖掘,根据每条限速的执行时间、设置范围,找出因限速影响到的列车及其所在区间、列车等级、运行方向等特征属性。
2.2 基于随机森林的不同限速条件下区间运行时分预测模型
不同限速条件下预测区间运行时分的随机森林模型如图2所示。
不同限速条件下基于随机森林的区间运行时分预测步骤如下。
(1)输入行车数据,含限速数据及其限速条件下所影响列车的行车数据,作为原始训练数据样本集,采用 bootstrap 取样方法,从原始训练数据样本集中随机且有放回地抽取m个与原始训练数据样本相同容量的样本集,形成m个样本集{S1,S2,…,Sm}。未被抽取的数据组成 OOB 样本集。
(2)通过特征提取初始化m个样本集,{S1,S2,…,Sm}={(X1,Y1),(X2,Y2),…,(Xm,Ym)},Xi为第 i 个样本集的特征属性向量,Yi为该限速条件下的区间运行时分。具体提取过程为:①对样本集中每一条限速数据初始化,由限速范围得到受限速影响的区间,再由限速时间得到受限速影响的列车行车数据,受限速影响的每趟车在每个区间的运行情况构成该训练集的一个子集。②取特征属性1为受限速影响的指定区间{Sec1,Sec2,…,Secn};取特征属性 2为列车类型{G,D,C};取特征属性3为列车运行所在线路及其方向{下行线正向,上行线正向,下行线反向,上行线反向};取特征属性4为列车区间始端和终端的通过/到开标志 {通过-通过,通过-到开,到开-通过,到开-到开};取特征属性5为限速值{200 km/h,160 km/h,120 km/h,80 km/h,45 km/h};取特征属性6为列车等级{高,中,低};取特征属性7为车站约束条件{区间始端站到发线数量,区间终到站到发线数量,区间始端站的作业时间,区间终端站的作业时间,最小发车间隔,最小接车间隔};取特征属性8为区间约束条件{图定区间运行时分,最小区间运行时分,最小追踪间隔时间}等。还可以根据具体场景扩充特征属性,同时确定该限速条件下的区间运行时分值。③m个样本集通过特征提取生成m个决策树{T1,T2,…,Tm}。对每一个决策树,按以下方法进行训练。从所有可选的k 个特征属性中随机选取 k1个特征属性,一般 k1=从这 k1个特征属性中选择导致最优划分的特征属性,将该节点根据选择的最优特征属性划分为2 个子节点。直到这棵决策树充分生长,所有叶节点对样的样本数都小于或等于 nmin,期间不作剪枝操作。单个决策树训练过程示意图如图 3所示。

图2 预测区间运行时分的随机森林模型Fig.2 Prediction model based on the principles of random forests
(3)聚合 m 棵决策树T1,T2,…,Tm,得到随机森林,所有决策树取众数 (简单投票) 得到输出。
(4)用 OOB 样本集评估模型,即预估总体泛化误差 PE*,PE* 的值由公式 ⑶ 得出,以提升该预测模型的精度。
2.3 随机森林算法在区间运行时分预测中的应用分析
应用随机森林算法预测区间运行时分的可行性分析如下。
(1)具有较高的预测准确度。随机森林是通过bootstrap 采样技术将若干个弱分类器组合起来的一个强分类器,将所有单棵决策树的弱学习算法进行组合来提升整个算法模型的学习能力,可使采用随机森林算法的区间运行时分预测模型具有较高的预测准确度。

图3 单个决策树训练过程示意图Fig.3 Sketch map of a decision tree learning
(2)可处理高维度数据。预测列车区间运行时分的所用到的数据集正好满足这样的需求,运行图的结构及影响列车运行时分的因素是高维度数据集。
(3)不容易过拟合。构建随机森林时每棵决策树都是基于 bootstrap 重采样及随机选取的特征子集来生成的,这样的生成方式使得算法不容易出现过拟合现象。
(4)可实现并行计算、训练速度快。随机森林中每棵决策树的构建过程是相互独立的,即决策树没有相互联系,因而可以实现多台机器上并行处理,提升预测模型的训练速度。
(5)可以得到特征属性重要性排名。特征属性重要性排名对研究区间运行时分预测模型具有很高的利用价值。区间运行时分预测模型的数据特征有很多,这些特征并不是完全没有噪声数据,因而需要得到特征重要性排名,然后研究重要性排名靠前的特征对区间运行时分预测模型的影响。
3 实例分析
以中国铁路成都局集团有限公司管内贵广高铁台运输组织的应用情况为背景,以贵广高铁台7个车站,12 个区间 (含上、下行区间) 作为研究对象构建仿真运算实例。采用从2016年9月1日至2017年8 月31日共12月的历史行车数据作为原始数据集。小碧线路所至从江站之间开行列车数量平均为42对/d,其中高速铁路列车 (G)6对/d,动车组列车 (D)36对/d。贵广高铁台 (8 ∶ 00—22 ∶ 00) 基本图如图4所示。

图4 贵广高铁台 (8 : 00—22 : 00) 基本图Fig.4 Basic flow of Guizhou-Guangzhou dispatcher control (8 ∶ 00—22 ∶ 00)
原始训练数据集中共含有200条限速数据,其中限速值为200km/h 的有119条,限速值为160km/h的有29条,限速值为120km/h 的有27条,限速值为80km/h 有24条,限速值为45km/h 有1条。训练数据中覆盖所有区间。采用 bootstrap 取样方法,从原始训练数据样本集中随机且有放回地抽取m个与原始训练数据样本相同容量的样本集,形成m个样本集,未被抽取的数据组成 OOB 样本集。根据限速设置的时间和起止里程,找出因限速波及到的区间和列车。依据每条限速执行的时间和设置的范围,受影响的列车将在涉及到的区间激发一次预测。以其中一条限速数据举例说明,贵广下行线 K73+275 至 K219+159,18 ∶ 00—21 ∶ 00,限速160km/h,由限速起止公里标范围得到受限速影响的区间为贵定县至都均东下行区间、都均东至三都县下行区间和三都县至榕江下行区间,由限速设置的起止时间得到受限速影响的列车有7趟:D2837、G2925、D2857、D2841、D2843、D3593 和 G2949。每趟车在受影响的每个区间的行车数据作为训练集中的一个子集,而该限速场景下 D2837 在都均东至三都县下行区间的特征属性为{都均东至三都县下行区间,D,下行线正向,到开-通过,160 km/h,中,(7,4,9,0,3,3),(11,8,3)},区间运行时分为16。以此方法得到各训练样本集中各限速数据的特征属性向量及其区间运行时分,同理初始化 OOB 样本集。m个样本集通过特征提取后训练生成m个决策树,聚合m个决策树得到随机森林预测模型,按取决策树众数的方式得到指定限速条件下列车的区间运行时分,同时用 OOB 样本集估计该预测模型的性能。
采用 scikit-learn 提供的随机森林分类器模型对不同限速条件下的列车区间运行时分进行预测。考察随机森林模型中决策树的个数对于总体预测性能的影响。设置 nums = np.arange (1,500,step = 5)。决策树个数对于预测准确率影响的试验结果如图5所示。考察随机森林模型中 max_depth 参数对于总体预测性能的影响。设置 max_depth =range (1,20)。决策树最大深度对预测准确率影响的试验结果如图6所示。
从图5可以看出随着决策树数量的增长,随机森林算法的性能很快上升并保持稳定,且对训练数据集一直能保持较好的拟合,对测试数据集的预测准确率在 90% 以上。随机森林算法能够较好地抵抗过拟合。从图6可以看出随着决策树最大深度的提高,随机森林的预测性能也在提高。提高决策树最大深度,每棵决策树的预测性能也在提高,同时决策树的多样性也在增大。实例验证结果表明,在不同限速条件下基于随机森林算法的列车区间运行时分预测具有可行性和有效性。

图5 决策树个数对于预测准确率影响的试验结果Fig.5 Numbers of decision trees on the accuracy of forecasts

图6 决策树最大深度对预测准确率影响的试验结果Fig.6 Maximal depth of a decision trees on the accuracy of forecasts
4 结束语
研究针对不同限速条件下列车在不同区间的运行时分预测问题,建立区间运行时分预测模型,引入随机森林算法对模型进行训练与求解,最后采用中国铁路成都局集团有限公司管辖范围内的贵广高铁台的历史行车数据进行仿真验证,验证结果表明所建立的模型和采用的算法具有可行性与有效性。在不同限速条件下有效预测列车在区间的运行时分是实现运行图自动化、智能化调整的基础,也是实现行车调度指挥系统自动化和智能化的重要条件之一。随机森林算法的引入对海量的跨时空行车数据的深度挖掘提供了一种有效的方法,为实现智能高速铁路调度指挥奠定了一定的理论基础。
[1] HAM J,CHEN Y,CRAWFORD M M,et al. Investigation of the Random Forest Framework for Classification of Hyperspectral Data[J]. IEEE Transactions on Geoscience &Remote Sensing,2005,43(3):492-501.
[2] EL-MANZALAWY Y,DOBBS D,HONAVAR V.Predicting Protective Bacterial Antigens Using Random Forest Classifiers[C]//In Proceedings of the ACM International Conference on Bioinformatics.Computational Biology and Biomedicine. Orlando:Association for Computing Machinery,2012:426-433.
[3] BELLOS C,PAPADOPOULOS A,ROSSO R,et al. Categorization of Patients’ Health Status in COPD Disease Using a Wearable Platform and Random Forests Methodology[C]//In Proceedings of the IEEE-EMBS International Conference on Biomedical and Health Informatics. Hong Kong:Institute for Electrical and Electronic Engineers,2012:404-407.
[4] 丁君美,刘贵全,李 慧. 改进随机森林算法在电信业客户流失预测中的应用[J]. 模式识别与人工智能,2015,28(11):1041-1049.DIND Jun-mei,LIU Gui-quan,LI Hui. The Application
( )( )of Improved Random Forest in the Telecom Customer Churn Prediction[J]. Pattern Recognition and Artificial Intelligence,2015,28(11):1041-1049.
[5] 袁志明,张 琦,黄 康,等. 基于随机森林的列车到站时间预测方法[J]. 铁道运输与经济,2016,38(5):60-63.YUAN Zhi-ming,ZHANG Qi,HUANG Kang,et al.Forecast Method of Train Arrival Time based on Random Forest Algorithm[J]. Railway Transport and Economy,2016,38(5):60-63.
[6] 齐雁冰,王茵茵,陈 洋,等. 基于遥感与随机森林算法的陕西省土壤有机质空间预测[J]. 自然资源学报,2017,32(6):1074-1086.QI Yan-bing,WANG Yin-yin,CHEN Yang,et al. Soil Organic Matter Prediction based on Remote Sending Data and Random Forest Model in Shaanxi Province[J]. Journal of Natural Resources,2017,32(6):1074-1086.
[7] BREIMAN L,SCHAPIRE E. Random Forests[J]. Machine Learning,2001,45(1):5-32.
[8] 蔡林霖. 随机森林的模型选择及其并行化方法[D]. 哈尔滨:哈尔滨工业大学,2012.
[9] 杨 浩. 铁路运输组织学[M].2版. 北京:中国铁道出版社,2006.
[10] 李小波,宴兴奎,郑平标,等. 山区铁路汛期运输组织应急调整对策探讨[J]. 铁道货运,2017,35 (1):5-9.LI Xiao-bo,YAN Xing-kui,ZHENG Ping-biao,et al.Discussion on Countermeasures of Transport Organization Emergency Adjustment of Mountain Railway in Flood Season[J]. Railway Freight Transport,2017,35 (1):5-9.

