城市轨道交通票务清分方法研究

龚 隽，靳文舟，郑亚晶

GONG Jun，JIN Wen-zhou，ZHENG Ya-jing

（华南理工大学 土木与交通学院，广东 广州 510640）

(School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510640，Guangdong，China)

0 引言

随着城市轨道交通的迅速发展，多方运营的模式被越来越多的城市采纳。城市轨道交通线网结构越发复杂，乘客在出行路径的选择上更具多样性，加之传统的票务清分手段在一票换乘的情况下已经不再适用，因而建立简单有效的票务清分体系已经成为运营中不可避免的难题。

在城市轨道交通中，由于无法获知乘客的具体路径选择，只能采用近似模拟的方法尽可能地反映客流在整体上及大多数情况下各路径的总体分配情况，主流思路是“双比例”清分，即首先确定各路径所分摊的客流比例，然后按照运营线路的贡献分担比例进行票务清分。由于国外大多数城市并不存在换乘上的清分过程，甚至在多运营方模式下也基本是各运营方单独核算，整个清分过程简单清晰，因而相关的研究较为缺乏。国内对票务清分的研究主要是在“双比例”清分方法的基础上，对路径的选择和比例的计算等方面不断改进创新。主要有：赖树坤[1]提出的方法考虑了 OD 间多条有效路径的选择，并以选择概率和各运营方对线路的投资建设比例作为收益清分的权重；贾楠[2]提出的“一保障，两比例，三阶段”方法引入了政策性保障，并对路径选择进行优化；韦强等[3]引入了路径代价的概念，提出多路径大概率优先综合清分方法，求解各路径的选择概率；陶玥等[4]提出的基于出行阻抗的有效路径选择概率模型为了保证收益的合理分配，在计算中引入换乘里程的概念。

目前的研究主要是把所有客流作为整体，运用广义费用进行客流分配和票务清分[5-9]，对于不同客流在路径选择中的差异性考虑较少。客流分配上的问题主要表现在：一些过于简便的分配方法虽然应用简单，但精度过低，与实际出入较大；一些复杂的模型变量及参数过多，在实际运用中难以有效标定。以广州轨道交通为例，广州轨道交通很早便开始采用“双比例”进行票务清分，在6号线建成之前主要将一个 OD 之间的全部客流分配到里程最短的有效路径上，这与实际客流情况有所差距。因此，在6号线建成之后，广州轨道交通提出多因素匹配法[10]，但其分配比例没有考虑客流的属性差异，不同路径之间的加速分摊计算规则在理论上也没有很好的科学支撑，该方法的结果虽然在某些典型 OD 上较为符合，但推广到全网之后，其效果究竟如何值得商榷。为此，从乘客路径筛选行为的角度进行探讨，重点研究“双比例”中的客流分配比例，根据客流属性分别进行清分，提出在实际运营工作中简单有效的清分算法。

1 城市轨道交通票务清分影响因素分析

影响城市轨道交通票务清分的因素有很多[11-13]，具体到每一 OD 间的票款收益分配时，由于各路径中线路的贡献分担比例相对固定，在乘客 OD 间的路径选择无法获知的情形下，有效路径的客流分配预估显得尤为重要。将影响清分的各种因素归纳为以下4类：乘客的经济社会因素、乘客的出行特征因素、轨道交通网络特性因素及运营方管理因素。票务清分影响因素如图1所示。

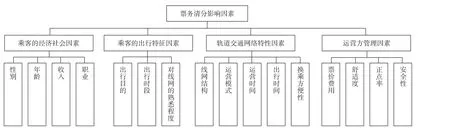
图1 票务清分影响因素Fig.1 The influencing factors on fare clearing

为了解相关因素对客流径路筛选的影响，对广州轨道交通乘客进行了问卷调研，选择出行时间、换乘次数 (换乘方便程度)、乘坐站数及乘坐里程作为路径选择首要考虑因素的乘客占调查总体的 90%，所占比例分别为 47%、20%、11% 和13%，其余因素如舒适度 (拥挤程度)、安全性、正点率、其他占比不大，均不超过 5%。由此可得在众多可选因素下，乘客主要以出行时间、换乘次数 (换乘方便程度)、乘坐站数和乘坐里程作为路径选择的首要考虑因素。

因此，在径路筛选时，可以将客流按以上4种因素进行客流划分，一般而言：①以出行时间作为主要考虑因素的客流对时间和效率的要求较高，一般是男性乘客、年轻乘客、学生与工薪阶层、高峰期客流等；②以换乘次数 (换乘方便程度) 作为主要考虑因素的客流倾向于选择换乘次数少且方便舒适的路径，一般是行动与换乘不便的老弱病残孕客流、收入水平较高的客流、以休闲娱乐为出行目的的客流、平峰期客流、舒适度要求较高的客流等；③以乘坐站数作为主要考虑因素的客流一般是外来人口客流、前往当地旅游的客流，因为其对时间、里程、换乘等因素没有及时形成相应的概念，更多只能考虑乘坐站数而选择相应的出行路径；④以乘坐里程作为主要考虑因素的客流多为私家车主、司机等经常开车的人群，其乘坐轨道交通的频率较低，一般习惯以里程衡量出行的支出。其他因素虽然也会引起乘客路径选择的改变，但相对而言与以上4种因素的影响有所差距，因而在客流划分中不作为主要因素进行考虑，部分因素如舒适度(拥挤程度) 会在阻抗构造分析中有所涉及。

需要指出的是，乘客在路径选择时更多是基于一种主观感受去考虑，最终路径的选择可能与实际情况有所偏差。而这在宏观上，就表现为基于同一考虑因素对路径进行选择的乘客，并不会集中在该因素下的“最短”路径上，而是在几条有效路径中呈现出一定的客流分配比例。

2 城市轨道交通票务清分算法

2.1 清分思路

首先按照属性来划分客流，即以出行时间、换乘次数 (换乘方便程度)、乘坐站数和乘坐里程作为客流划分的4个主要筛选因素，通过客流调查得到各主要因素的客流占比；然后在各类客流中分别进行“双比例”清分。

（1）根据一定的清分规则，每一类客流分别对其 OD 选取有效路径并进行客流分配，再将对应的路径分配比例按路径进行累加，从而得到“双比例”中各路径所分配的客流比例。

（2）根据路径中各运营线路的里程比进行该OD 的收益分配，按路径进行累加，进而完成各运营方或线路的清分。

2.2 阻抗构造

2.2.1 出行时间

出行时间指乘客乘坐轨道交通由起点站到终点站所花费的全部时间，包括乘车时间和换乘时间等。在出行时间因素条件下，构造出行阻抗如下。

出行阻抗 = 列车各区间运行时间 + 列车中间站停站时间+乘客平均换乘时间，即

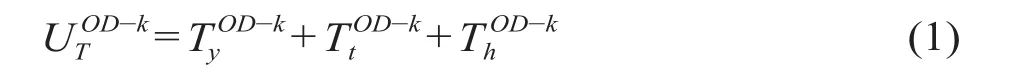
k为由站 O 至站 D 的第 k 条路径上，列车在各区间上的运行时间之和；为由站 O 至站 D 的第 k 条路径上，列车在各站的停站时间之和；为由站 O 至站 D 的第 k 条路径上，列车在各换乘站的换乘时间之和。

2.2.2 换乘次数 (换乘方便程度)

设计反映换乘次数的阻抗时，除换乘次数外，换乘的时间、换乘方式、换乘舒适度等因素都应该在其中有所体现。

乘客在换乘站 R 从线路 i 换乘到线路 j 的换乘时间由换乘步行时间和换乘等候时间2部分组成，而线路间的列车发车频率会影响乘客的换乘等候时间，这里换乘等候时间取发车时间间隔的一半，即

如果换乘时间较为接近，换乘方式的差异显然也会影响到乘客选择的意愿。因此，需要根据换乘站换乘形式的差异对进行修正。

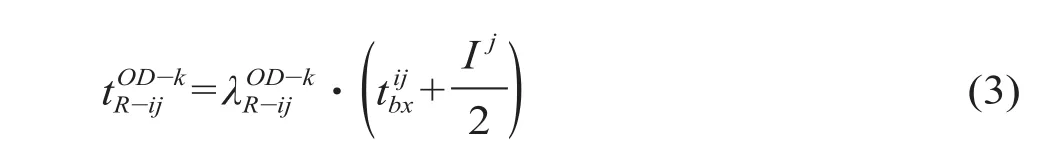
表1 不同换乘形式下 λ 的取值Tab.1 The value of under different transfer modes

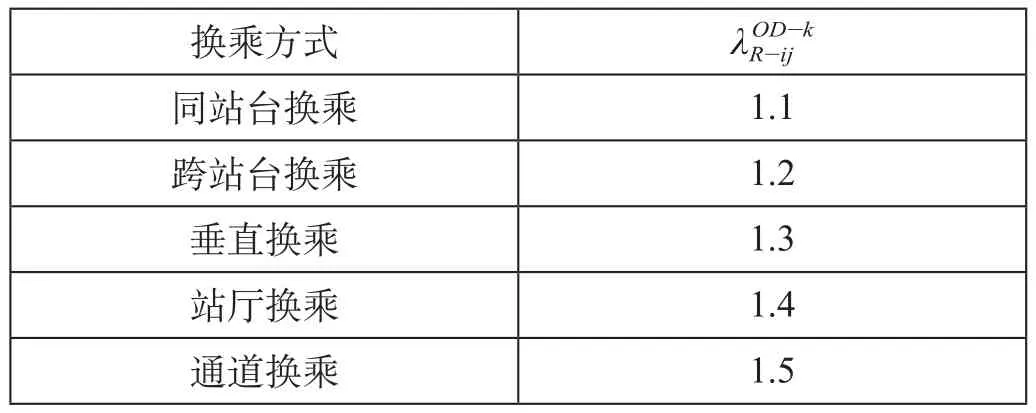
表1 不同换乘形式下 λ 的取值Tab.1 The value of under different transfer modes

换乘方式 λROD-ij-k同站台换乘 1.1跨站台换乘 1.2垂直换乘 1.3站厅换乘 1.4通道换乘 1.5

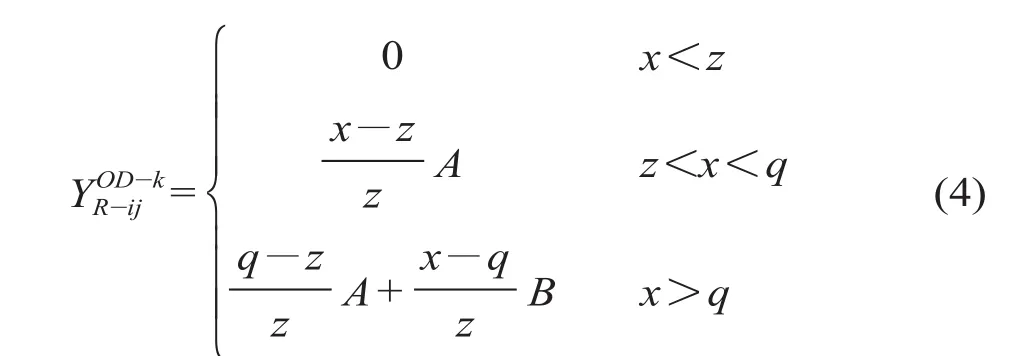
式中：x 为由站 O 至站 D 的第 k 条路径上线路 j 最拥挤路段的客流量；z 为换乘后的列车座位数；q 为换乘后的列车能容纳的最大乘客数(列车定员载荷)；A 为换乘后的列车一般拥挤时，确定的额外开销系数；B 为换乘后的列车过度拥挤时，确定的额外开销系数。

根据相关研究[14]，在不同情况下 A，B 取值如表2所示。

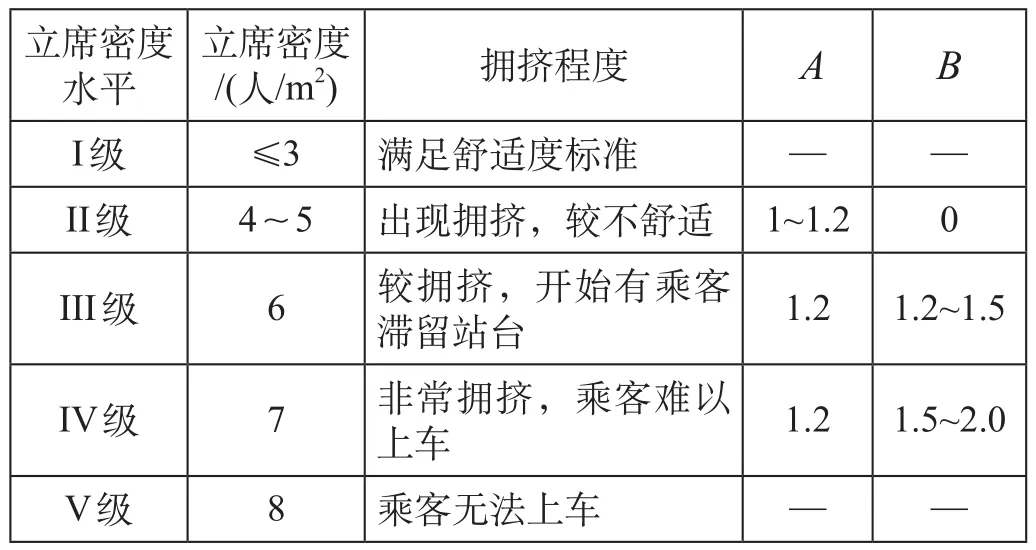
立席密度水平立席密度/(人/m2) 拥挤程度 A B I 级 ≤3 满足舒适度标准 — —II 级 4～5 出现拥挤，较不舒适 1～1.2 0 III 级 6 较拥挤，开始有乘客滞留站台 1.2 1.2～1.5 IV 级 7 非常拥挤，乘客难以上车 1.2 1.5～2.0 V 级 8 乘客无法上车 — —

在换乘次数 (换乘方便程度) 这一因素条件下，构造出行阻抗如下。

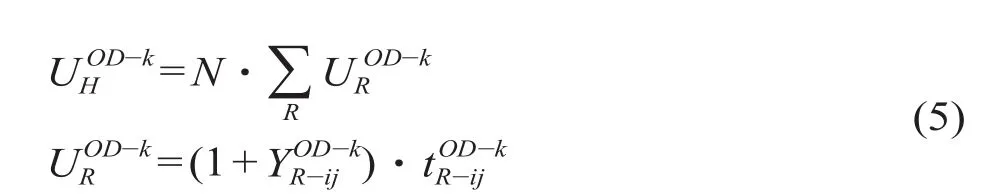
2.2.3 乘坐站数

乘坐站数是指乘客选择的路径所包含的车站数，包括终点站但不包括起始站，并且每个换乘站仅算一站。构造出行阻抗如下。

2.2.4 乘坐里程

乘坐里程是指乘客搭乘一次轨道交通的路径长度，所选路径的乘坐里程即为路径中各线路的里程之和。构造出行阻抗如下。

2.3 模型建立

结合各选取因素出行阻抗的构造，票务清分模型如下。

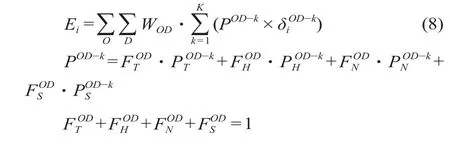
式中：Ei为线路i的分配收益；WOD为站 O 至站 D的总收益；POD-k为由站 O 至站 D 的第 k 条路径上的客流分配比例；为线路 i 在由站 O 至站 D 的第 k 条路径上的里程比重。

对于客流路径分配比例的计算方法，运用Logit 模型进行求解，同时根据传统 Logit 模型的缺陷，取路径的相对出行阻抗比值来予以改进，并应用到各类客流的路径分配比例的计算中。

以出行时间作为径路选择首要考虑因素的客流为例说明。

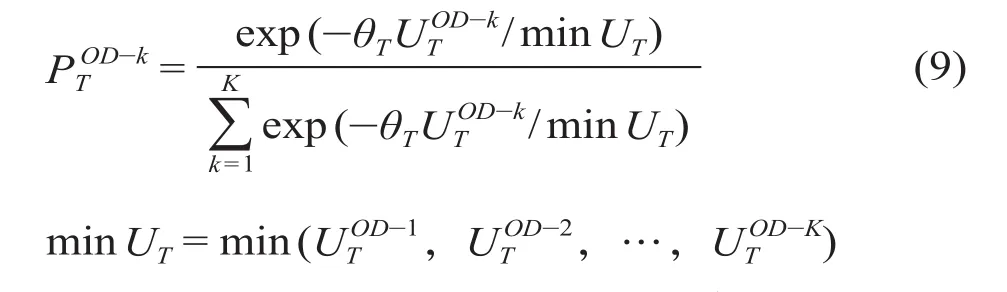
式中：θT为 Logit 模型的相关系数，这一系数的值可近似反映这类乘客对线路的熟悉程度；K 为由站 O 至站 D 的有效路径的数目。其余3类客流的计算方法同上。

通过调查获取典型 OD 对的路径属性值及相关客流数据，并对模型的变量及参数进行标定，在确定相关系数后，将根据模型算得的客流分配比例与实际的结果相比较，若二者的误差在可接受的允许范围内[14]，模型的准确性和实用性便得到了验证。

3 算例分析

3.1 OD 选取

为了检验清分模型的准确性及实用性，选取广州轨道交通中2组典型OD 作为径路调研 OD，分别为同和—广州火车站、五山—广州东站。再根据相关的清分规则[10，15-17]，筛选 OD 的有效路径。从同和到广州火车站的有效路径如图2所示。在这组 OD 中，共有有效路径2条：①路径 A 是乘坐3号线北延段从同和经过3站到嘉禾望岗，并通过通道换乘的方式换乘至2号线，再经过8站到广州火车站；②路径 B 是乘坐3号线北延段从同和经过3站到燕塘，并通过通道换乘的方式换乘至6号线，然后经过4站到区庄 (由于沙河未开通，相关数据暂不对其进行考虑)，并通过垂直换乘的方式换乘至5号线，再经过3站到广州火车站。

从五山到广州东站的有效路径如图3所示。在这组 OD 中，共有有效路径3条：①路径 A 是乘坐3号线从五山经过1站到天河客运站，并通过通道换乘的方式换乘至6号线，然后经过1站到燕塘，并通过通道换乘的方式换乘至3号线北延段，再经过1站到广州东站；②路径 B 是乘坐3号线从五山经过4站到体育西路，并通过站厅换乘的方式换乘至1号线，再经过2站到广州东站；③路径 C 是乘坐3号线从五山经过4站到体育西路，并通过跨站台换乘的方式换乘至3号线北延段，再经过2站到广州东站。

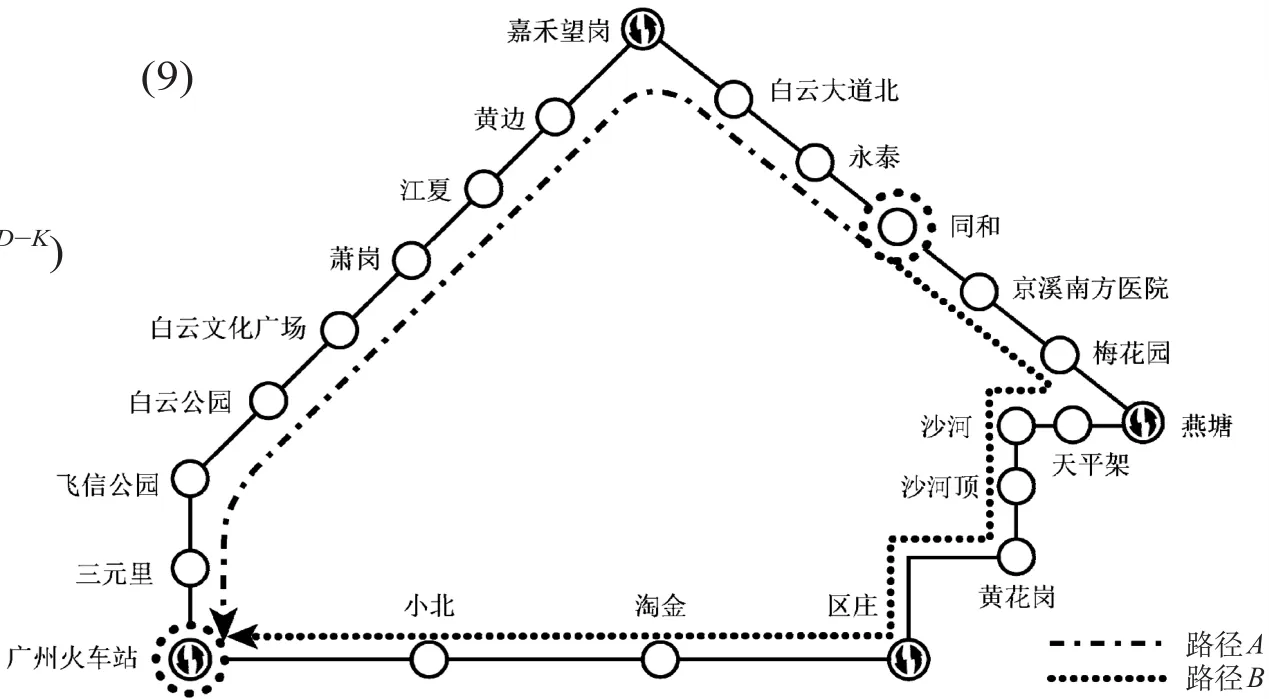
图2 从同和到广州火车站的有效路径Fig.2 The effective routes from Tonghe to Guangzhou railway station

图3 从五山到广州东站的有效路径Fig.3 The effective routes from Wushan to Guangzhou east railway station

3.2 模型应用

3.2.1 系数确定

结合从同和到广州火车站各有效路径的属性值，标定相关参数。根据调研数据，由公式得到各选取因素下路径的出行阻抗如表3所示。

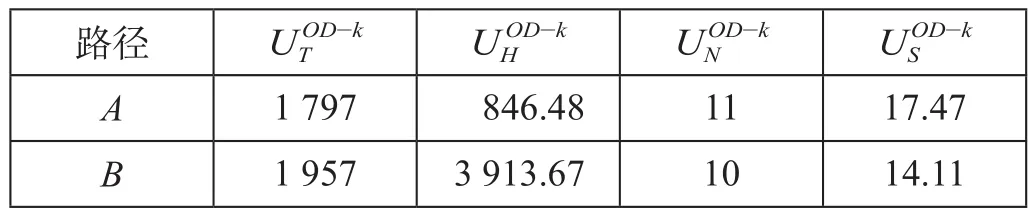
表3 各选取因素下路径的出行阻抗Tab.3 Impedance of each route under different selected factors

以出行时间、换乘次数(换乘方便程度)、乘坐站数及乘坐里程为主要考虑因素的4类客流中，各主要因素客流中路径选择概率如表4所示。

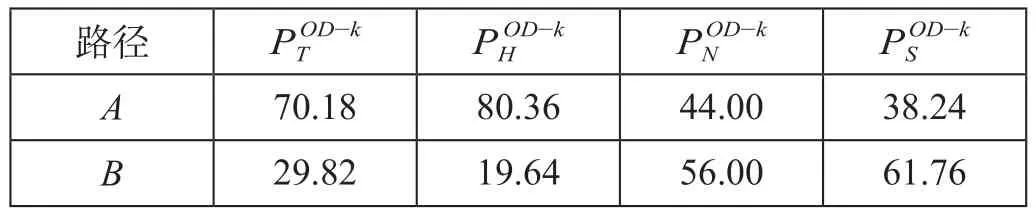
表4 各主要因素客流中路径选择概率 %Tab.4 Probabilities of the routes chosen by major passenger groups

再由公式得各类客流 Logit 模型的相关系数θT= 9.52，θH= 0.38，θN= 2.41，θS= 2.06，从而确定模型的系数。

3.2.2 客流分配

仅考虑以出行时间、换乘次数 (换乘方便程度)、乘坐站数及乘坐里程为主要考虑因素的4类客流，将其调研数据中各类客流占4类客流总体的百分比作为各主要因素客流的概率，即：

根据另一调研 OD (五山—广州东站) 的相关数据，通过模型得到各选取因素下每条有效路径的出行阻抗，计算出模型所得各主要因素客流中路径的选择概率如表5所示，调查所得各主要因素客流中路径的选择概率如表6所示。

比较表6的实际结果可知，以出行时间、换乘次数 (换乘方便程度) 为主要考虑因素的客流结果与模型计算的概率误差较小，而以乘坐站数和乘坐里程为主要考虑因素的客流则在部分选择上有一定的偏差，可能是由于这2类客流在总体客流占比相对较小，一旦部分参与调查的乘客调研问卷模糊或不真实，将对路径选择结果造成较大的影响，导致实际结果与模型所得的概率有一定差异。

表5 模型所得各主要因素客流中路径的选择概率 %Tab.5 Probabilities of the routes chosen by major passenger groups calculated by the proposed model

表6 调查所得各主要因素客流中路径的选择概率 %Tab.6 Probabilities of the routes chosen by major passenger groups obtained from surveys

模型与调查所得的客流分配结果比较如表7所示。由表7可知，从客流总体的角度分析，各路径下模型与调查所得结果的差额均在 5% 内，结果比较接近，并且与实际情况相符。而出现一定偏差的2类客流在总体客流的占比相对较小，对总体路径的选择影响不大，总体误差较小。

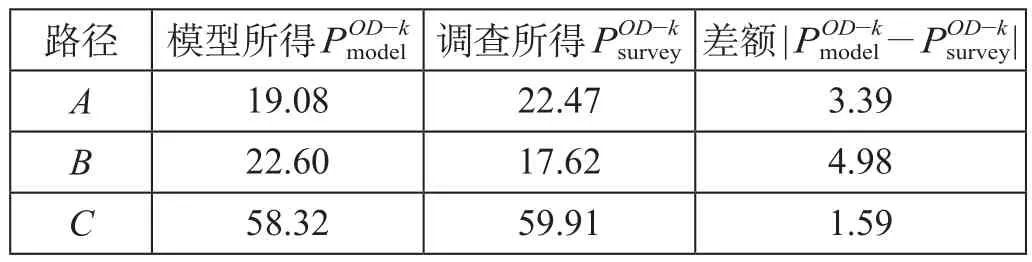
表7 模型与调查所得的客流分配结果比较 %Tab.7 Comparisons of the results of passenger distribution obtained from the proposed model and surveys

3.2.3 清分结果

根据相应线路的里程数据，再结合客流分配比例，线路在各路径的里程分担比例如表8所示。

从五山到广州东站的单程票价为3元，这里假设该 OD 间所有乘客的出行费用均为3元，再结合某日从五山到广州东站的轨道交通客流量为 1214人，由公式可得 OD 间各线路的清分比例及收益分配如表9所示。

表8 线路在各路径的里程分担比例 %Tab.8 The mileage sharing ratios of different lines among different routes

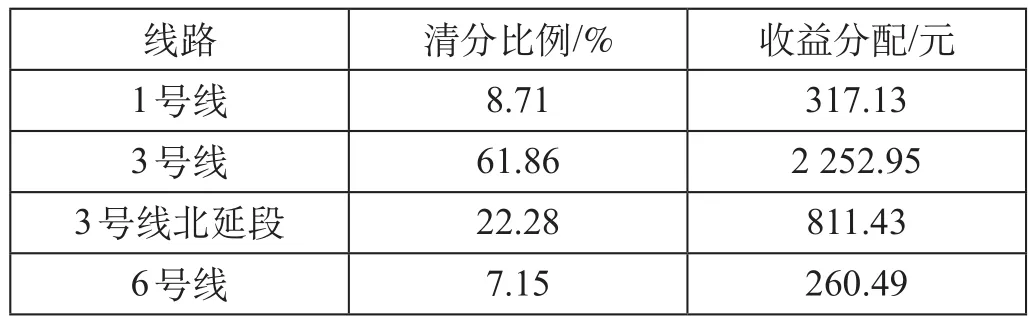
表9 OD间各线路的清分比例及收益分配Tab.9 The fare clearing and distribution ratios of each line within OD

由此便完成了该 OD 间票款收益的清分。3 号线和3号线北延段由于在至少2条有效路径上都有一定的里程比例，最终的清分比例相对较大，而 1号线和6号线也得到了相应的清分比例。

再与广州轨道交通的传统清分算法得出的收益分配进行结果比较，清分结果比较如表10所示。由表10可知，传统算法中只根据里程最短路径 (路径 A) 进行清分，收益分配没有涉及到1号线；同时在实际调查中由于换乘的便捷程度，更多的乘客选择了路径 C，可见传统算法中6号线的收益分配过高。所提出的清分算法更加能够反映乘客实际路径选择，解决了传统算法中存在的问题，清分结果更加公平合理。

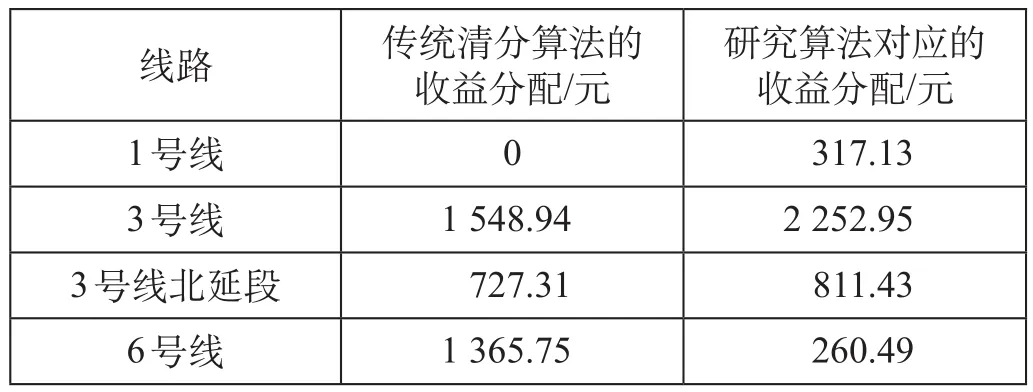
表10 清分结果比较Tab.10 Comparisons of the results of fare clearing

综上，尽管在部分因素客流中一些路径的选择概率与实际调查结果存在一定偏差，但从总体的角度看，各路径下模型与调查所得结果的误差较小，与实际情况相符，说明该模型具有一定的准确性和实用性。

4 结束语

为了保证收益能公平合理地分配到城市轨道交通各运营方或运营方的各条线路上，需要建立简单有效的清分体系。在实际运营中，乘客路径选择行为大大增加了清分的难度。即便是同一 OD 间，由于考虑的因素有所差异，乘客在有效路径的选择中也极为不同，甚至是以同一因素为考虑首选的乘客，由于自身感知及判断标准的不同，最终选择的路径也有差异。因此，如何准确把握乘客路径选择行为，是研究清分问题的关键所在，这也将是今后城市轨道交通票务清分的主要研究方向。

[1] 赖树坤. 城市轨道交通票务清分方法研究[D]. 北京：北京交通大学，2008.

[2] 贾 楠. 城市轨道交通票务清分问题研究[D]. 北京：北京交通大学，2008.

[3] 韦 强，谢宗毅，诸仕荣，等. 基于概率模型的轨道交通清分算法[J]. 城市轨道交通研究，2009(9)：43-46，51.WEI Qiang，XIE Zong-yi，ZHU Shi-rong，et al. Fare Clearing Algorithm based on Probabilistic Model for Urban Rail Transit[J]. Urban Mass Transit，2009(9)：43-46，51.

[4] 陶 玥，张冬泉. 城市轨道交通票款清分方法[J]. 都市快轨交通，2010(4)：16-19.TAO Yue，ZHANG Dong-quan. Fare Clearing Model for Urban Rail Transit[J]. Urban Rapid Rail Transit，2010(4)：16-19.

[5] QIAO Ke，ZHAO Peng，QIN Zhi-peng. Passenger Route Choice Model and Algorithm in the Urban Rail Transit Network[J]. Journal of Industrial Engineering and Management，2013，6(1)：113-123.

[6] WANG Da-lei，YAO En-jian，YANG Yang，et al. Modeling Passenger Flow Distribution based on Disaggregate Model for Urban Rail Transit[J]. Advances in Intelligent Systems &Computing，2014(215)：715-723.

[7] 徐永实，曲思源，徐瑞华. 城市轨道交通客流实时分布算法研究[J]. 铁道运输与经济，2017，39(5)：82-87.XU Yong-shi，QU Si-yuan，XU Rui-hua. Research on Realtime Algorithm of URT Passenger Flow Distribution[J].Railway Transport and Economy，2017，39(5)：82-87.

[8] 陈 阳. 基于复杂换乘的城市轨道交通客流分配[D]. 成都：西南交通大学，2017.

[9] 李 原. 城市轨道交通网络换乘客流分配研究[D]. 成都：西南交通大学，2017.

[10] 吕利民. 广州市轨道交通系统线网票务收益清分应用研究[D]. 广州：华南理工大学，2006.

[11] 廉 菲. 城市轨道交通票务清分系统研究[D]. 西安：长安大学，2016.

[12] 周玮腾，韩宝明，冯 超. 城市轨道交通网络客流分配模型和算法综述[J]. 系统工程理论与实践，2017，37(2)：440-451.ZHOU Wei-teng，HAN Bao-ming，FENG Chao. A Review of Passenger Flow Assignment Model and Algorithm for Urban Rail Transit Network[J]. System Engineering-Theory &Practice，2017，37(2)：440-451.

[13] 晏莉颖，孟祥佩. 轨道交通对居民交通方式选择的影响研究[J]. 铁道运输与经济，2018，40(1)：100-105.YAN Li-ying，MENG Xiang-pei. Effect of Rail Transit on Residents' Choice of Traffic Modes[J]. Railway Transport and Economy，2018，40(1)：100-105.

[14] 毛保华. 城市轨道交通网络管理及收入分配理论与方法[M].北京：科学出版社，2007.

[15] 潘 祥. 网络状态下的城市轨道交通清分方法研究[D]. 成都：西南交通大学，2014.

[16] 毕丹妮. 城市轨道交通无障碍换乘下票务清算问题研究[D].成都：西南交通大学，2014.

[17] 马 芳. 城市轨道交通客流分配研究[D]. 成都：西南交通大学，2013.