铁路桥梁墩台刚度对无缝线路的影响

蔡敦锦

(中国铁路设计集团有限公司，天津 300140)

1 概述

在桥上铺设无缝线路轨道结构时，钢轨将同时承受温度力与桥梁附加纵向力的共同作用。力的作用是相互的，这些附加在钢轨上的纵向力也会反作用在梁跨上。每一简支梁的跨梁一般由固定支座与活动支座支撑，活动支座受力后会通过移动释放力，梁跨受到的力会传递到固定支座上，而固定支座与桥墩固结，最终钢轨对梁跨的反作用力传递至桥墩。桥墩为竖向支撑，在其弹性受力范围内，受到横向力时会产生弹性变形，从而导致桥墩顶部向着受力方向发生纵向位移，桥墩顶部发生的纵向位移又会反过来对梁体纵向位移的分布产生影响[1-2]。桥梁墩台纵向水平刚度一般定义为：桥梁墩台上的支承垫石在受力时产生一个单位的纵向水平位移时所需要的纵向力的大小[3]。从桥梁与钢轨相互之间作用的机理来看，墩台纵向水平刚度对梁体纵向位移分布的影响比较显著，这也必然会影响到钢轨与桥梁所受到的纵向附加力[4-6]。因此，在进行桥上无缝线路设计时，应将其对桥上无缝线路纵向附加力的影响因素考虑进来。通过建立简支梁及连续梁组合的桥上无缝线路计算模型，重点分析墩台纵向水平刚度对钢轨纵向附加力的影响。

2 计算背景

2.1 计算模型

基于桥上无缝线路桥梁与钢轨间相互作用的机理及轨道结构与桥梁结构的受力特点，建立线路、桥梁、墩台一体化计算模型[7-11]，以连续梁为例(如图1所示)。计算时充分考虑了墩台受力特性，认为线路纵向阻力采用弹簧单元来模拟较为合理(钢轨与桥梁单元均采用梁单元进行模拟)。文献[1，7，12]等均应用此模型进行了一系列无缝线路相关分析，证明了此模型的准确性与可靠性。

图1 线桥墩一体化计算模型

2.2 计算参数

在本模型中，经过合理简化并充分考虑到实际的边界情况，选取5跨32m简支梁进行模拟计算，墩台上的固定支座统一设置于简支梁的左边墩台上，选用《时速250公里客运专线铁路有砟轨道后张法预应力混凝土简支箱梁》(通桥(2008)2221A)通用图设计中的通用梁体结构，梁体高度为2.8 m，桥台纵向水平刚度取值为3 000 kN/cm(双线)，桥墩纵向刚度取值为350 kN/cm(双线)[12]；桥梁日温差取15 ℃，线路纵向阻力依据《铁路无缝线路设计规范》设计规定中的双线性阻力形式[13]。连续梁计算模型为2×32 m简支梁+(32+48+32) m连续梁+2×32 m简支梁，模型中支座布置情况如图2所示，连续梁模型中墩台纵向水平刚度按1 000 kN/cm(双线)计算，线路纵向阻力参数及桥梁日温差参照简支梁模型取值[14-15]。

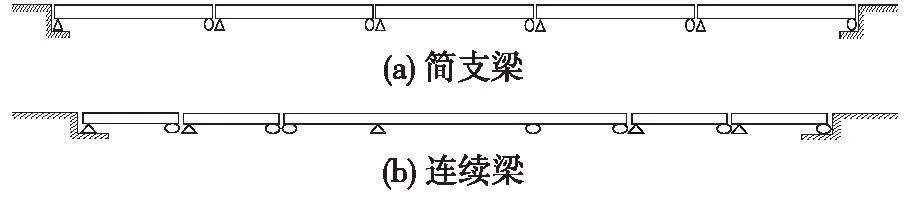
图2 桥梁支座布置

2.3 计算工况

分别选取桥墩纵向刚度基准的0.5倍、1倍、2倍、5倍及刚性5种工况进行计算，分析不同工况下钢轨、墩台的纵向力与钢轨纵向位移的变化规律。

3 计算结果及分析

3.1 伸缩力计算

伸缩力计算时，不考虑轨面制动力及列车竖向荷载。桥梁在温度作用下的伸缩位移以及设有伸缩调节器后的轨条伸缩位移为主动荷载，按单股钢轨进行计算，桥梁两端轨条伸入路基上的计算长度取150 m。

(1)墩台刚度的影响

根据《铁路无缝线路设计规范》计算钢轨伸缩附加力时，有砟轨道结构时混凝土梁体温度差为15 ℃。随着墩台纵向水平刚度的增加，桥上钢轨的最大伸缩附加压力与墩台受到的纵向力变化情况如图3所示。

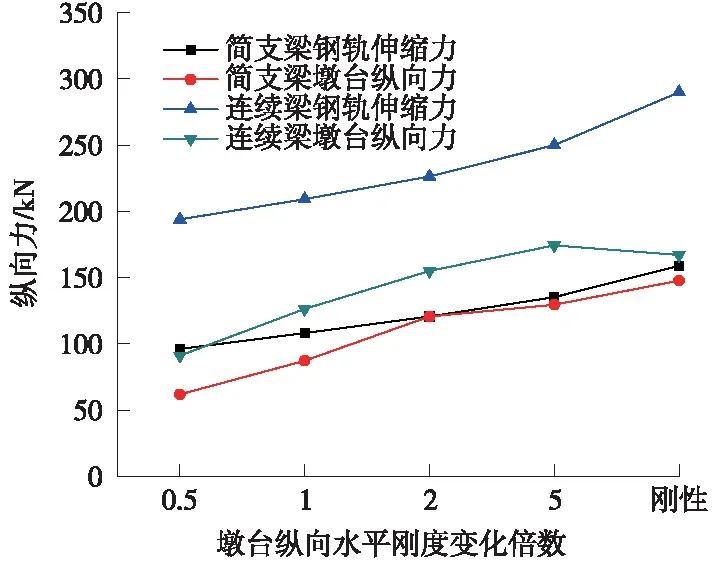
图3 钢轨伸缩力、墩台纵向力变化情况

两种不同模型计算得出的桥上钢轨最大伸缩压力、墩台所受最大纵向力及钢轨发生最大伸缩位移变化值见表1。

由表1可知，钢轨伸缩力、墩台纵向力及钢轨位移均随着墩台刚度的增大而增加(增加幅度均呈现不同程度的减缓)，墩台纵向力与钢轨位移随墩台水平刚度的变化相对钢轨最大伸缩力的变化要平缓得多。从桥梁与钢轨的相互作用机理来看，桥梁墩台刚度越大，其受到钢轨反作用力后位移变化值越小；越靠近固定支座的位置，桥梁与钢轨位移相同点两侧受到的阻力之和也越大，导致此点钢轨与桥梁所受的纵向阻力越大。

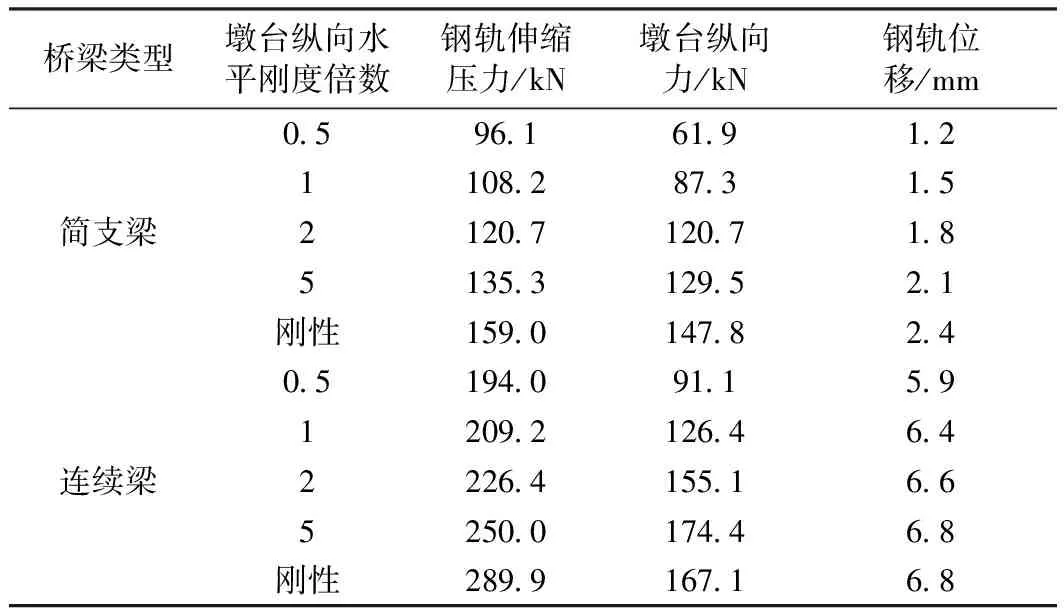
表1 墩台刚度对伸缩力的影响

由此可看出，钢轨伸缩附加力受桥梁墩台纵向水平刚度影响较大；为保证钢轨伸缩附加力的值在一定范围内，桥梁墩台的纵向水平刚度应通过详细计算与试验后合理选取，不宜过大。

(2)墩台自身水平位移的影响

对于超高墩桥梁，比如墩高超过100 m时，大风、地震、甚至阳光的照射均可能导致墩顶的纵向位移，该位移也是桥上无缝线路系统中线桥相互作用的主动力，可导致线-桥-墩系统内力的重分布。在图2模型中，其他参数不变，考虑简支梁与连续梁中间主跨桥墩分别发生0 mm、-2 mm、-4 mm、2 mm及4 mm位移5种工况下，利用模型计算钢轨伸缩附加力、墩台纵向力的变化，计算结果如图4所示(规定桥墩纵向位移以向右为正)。

3.2 挠曲力计算

挠曲工况计算时，根据《铁路无缝线路设计规范》规定，荷载类型取中-活载，入桥类型为从左至右，其余计算参数同前。考虑刚性桥墩与弹性桥墩两种情况，计算得到连续梁上钢轨挠曲力的分布情况如图4所示。

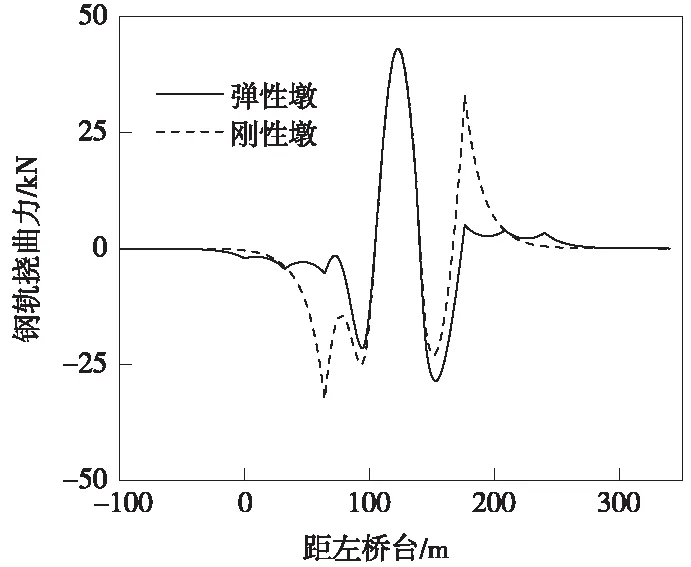
图4 桥墩刚度对连续梁挠曲力的影响

随着墩台刚度的增加，简支梁及连续梁上钢轨承受的最大挠曲附加压力、墩台承受的最大纵向力、钢轨承受的最大纵向位移的变化情况如表2所示。

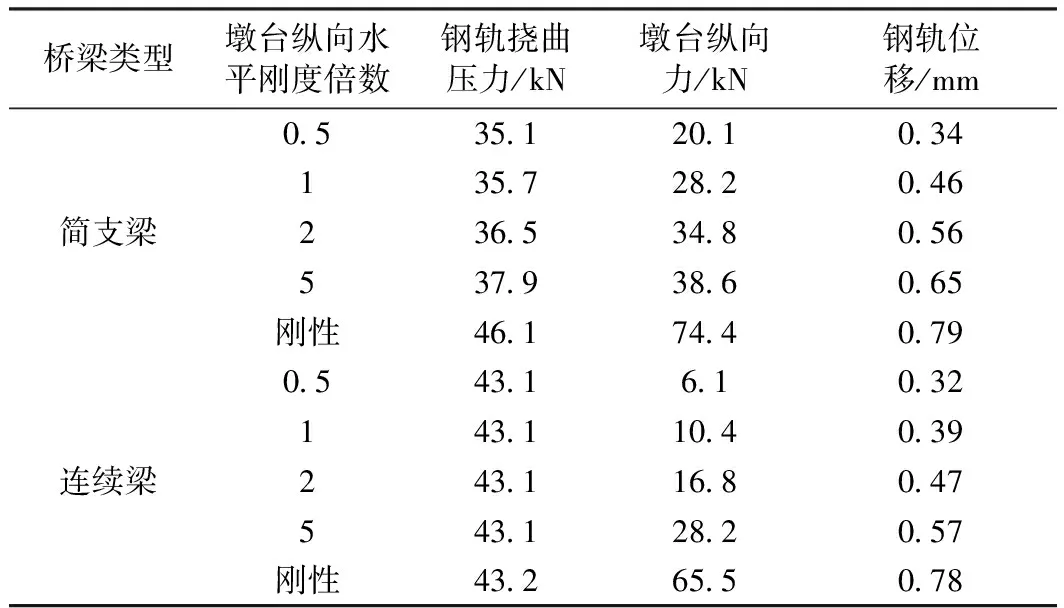
表2 墩台纵向水平刚度对挠曲力的影响

由图4可知，连续梁桥上钢轨挠曲附加力的分布情况随墩台纵向水平刚度的不同而有所变化。引起这种现象的主要原因是：由于简支梁桥墩纵向水平刚度的增大，使得连续梁与简支梁交接处的桥梁相对纵向位移增大，从而导致连续梁端部位置处的钢轨挠曲附加力随之增大，而连续梁上钢轨附加挠曲力则主要由连续梁自身的纵向位移波动所决定。

由表2可知，随着桥梁墩台刚度的增大，简支梁与连续梁上钢轨挠曲压力均随之变大；但是简支梁变化幅度较连续梁要大；连续梁上钢轨挠曲压力随墩台纵向水平刚度的增加几乎没有变化。两种模型计算结果中的墩台纵向力与钢轨位移均随着墩台刚度的增大而增大，且变化较为明显。

综上所述，桥梁墩台纵向水平刚度的变化对连续梁挠曲压力的影响可以忽略不计，但其对简支梁挠曲力的影响应引起足够重视，在简支梁桥上无缝线路设计中应充分予以考虑。

3.3 制动力计算

在进行制动力计算时，列车制动时车轮与轨面摩擦系数取为0.164，采用的荷载类型为中-活载，规定荷载从左至右入桥。随着桥梁墩台纵向水平刚度的变化，可计算得到简支梁及连续梁上钢轨制动力、墩台纵向力的变化情况(如图5所示)。

图5 制动力随墩台刚度变化情况

钢轨制动力、墩台纵向力、钢轨纵向位移及梁轨相对位移的变化情况如表3所示。

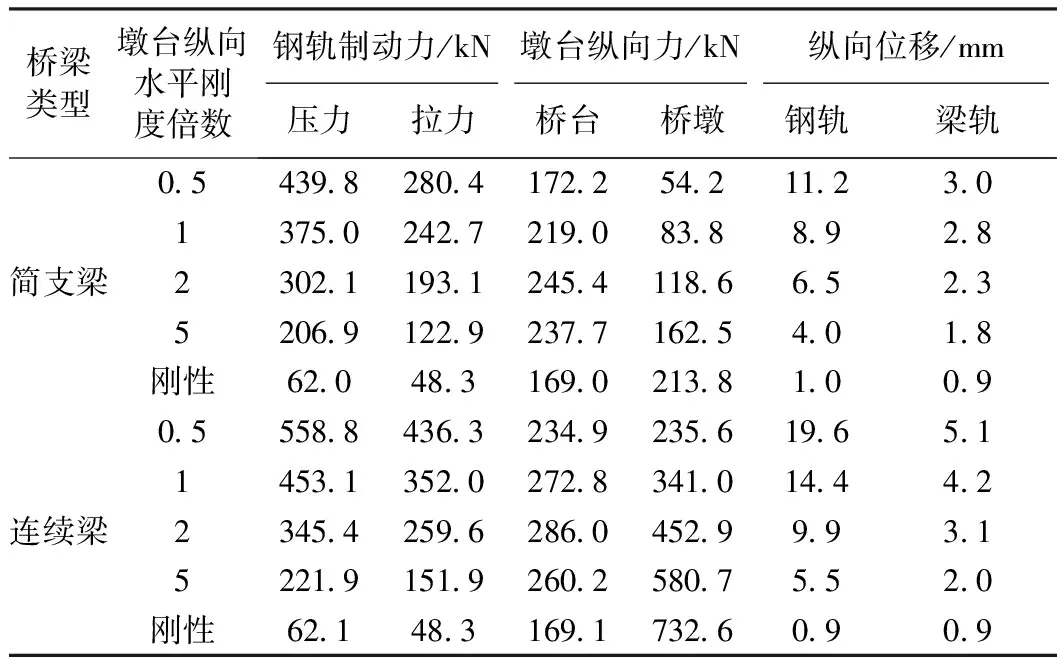
表3 墩台纵向水平刚度变化的影响

由表3可知，随着墩台纵向水平刚度的增大，钢轨制动压力与拉力均随之减小，变化较为明显；钢轨纵向位移与梁轨相对位移均随着墩台纵向水平刚度的增大而减小(减小趋势逐渐平缓)；墩台纵向力随着墩台刚度的增大而增大，当墩台纵向水平刚度增加到一定值后，桥台承受的纵向力反而减小，这是由于当墩台纵向水平刚度增加到某一值后，中间桥墩会承受大部分的荷载，从而使得左端桥台承受的纵向力减小。

由此可以得出，墩台纵向水平刚度对钢轨制动力有较大的影响，在进行无缝线路设计时应合理选取墩台纵向水平刚度。

3.4 断缝值计算

仅以连续梁计算模型为例，取钢轨降温幅度值为50 ℃，假设钢轨断缝发生在连续梁右端梁缝处，经计算，得到钢轨断轨力及墩台受力分布情况(如图6所示)，钢轨断缝值随桥梁墩台纵向水平刚度增大的变化情况(如图7所示)。

图6 钢轨及墩台纵向力分布

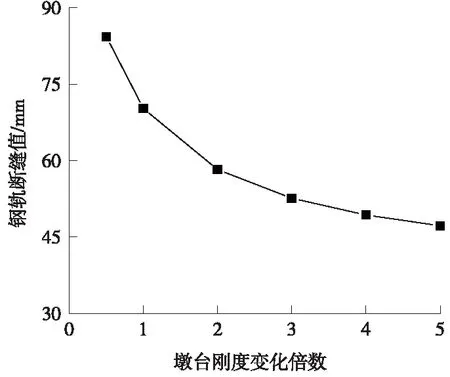
图7 钢轨断缝值变化情况

由图6可知，钢轨温度力的分布与钢轨纵向力的分布较为一致；断缝位置附近桥梁墩台所受纵向力较大，左侧连续梁桥墩纵向力约为456.1 kN，右侧简支梁桥墩纵向力约为221.1 kN。出于安全考虑，规范中直接规定按桥梁长度乘以线路极限阻力(不超过固定区温度力)作为墩台断轨力检算值。

由图7可知，钢轨断缝值随着墩台刚度的增大而减小，这主要是由于随着墩台刚度的增大，其对钢轨伸缩的约束作用增大。

由此可以得出，在进行无缝线路设计时，从断轨力的角度考虑，墩台纵向水平刚度取较大值是有利的，应限制桥梁墩台的最小水平刚度。

4 结论

(1)钢轨伸缩附加力受桥梁墩台纵向水平刚度影响较大；为了保证钢轨伸缩附加力的值在一定范围内，桥梁墩台的纵向水平刚度应通过详细计算与实验后合理选取，不宜过大。

(2)墩台自身的纵向水平位移对桥梁钢轨相互作用系统的纵向受力情况有着调节作用；墩台自身的纵向水平位移能够改变桥梁轨道系统的纵向受力情况，建议在进行无缝线路设计计算时，应考虑桥梁墩台自身位移较大时对无缝线路设计的影响。

(3)桥梁墩台纵向水平刚度的变化对连续梁挠曲压力的影响可以忽略不计，但其对简支梁挠曲力的影响应引起足够重视，在简支梁桥上无缝线路设计中应充分予以考虑，以防出现不必要的损失。

(4)墩台纵向水平刚度对钢轨制动力有着较大的影响，在进行无缝线路设计时应合理选取墩台纵向水平刚度。

(5)在进行无缝线路设计时，从断轨力的角度考虑，墩台纵向水平刚度取较大值是有利的。因此，应限制桥梁墩台的最小水平刚度。

[1] Yi Sirong. Railway Engineering[M](2nd ed). Beijing: China Railway Publishing House， 2009

[2] Esveld C. Modern Railway Track[M]. MRT-Productions， Zaltbommel， 2001

[3] 熊震威，谢铠泽，刘浩，等.列车制动对刚构桥上无缝线路梁轨相对位移的影响研究[J].铁道标准设计，2013(10):10-14

[4] 李志辉.铁路高墩、大跨、长联简支梁桥上无缝线路桥墩纵向水平线刚度优化[D].长沙：中南大学，2011

[5] 张迅.常用跨度连续梁桥墩顶纵向水平线刚度限值研究[D].成都：西南交通大学，2008

[6] 申全增.高速铁路小跨度梁桥墩设计纵向水平刚度限值的探讨[J].铁道标准设计，1997(12)

[7] 刘浩，魏贤奎，熊震威，等.线路纵向阻力形式对桥上无缝线路计算影响[J].铁道标准设计，2013(10):61-64

[8] 广钟岩，高慧安.铁路无缝线路[M].北京:中国铁道出版社，2005

[9] 魏峰.制动力作用下铁路桥墩墩顶纵向水平刚度变化模型试验研究[J].铁道工程学报，2007(12):49-52

[10] 徐庆元，陈秀方，李树德.高速铁路桥上无缝线路纵向附加力研究[J].中国铁道科学，2006(3):8-12

[11] 徐庆元，周小林，杨晓宇.桥上无缝线路附加力计算模型[J].交通运输工程学报，2004(1):25-28

[12] 蔡敦锦，颜乐，李悦，等.桥梁参数对桥上无缝线路伸缩力的影响分析[J].铁道标准设计，2014(7):30-34

[13] 魏峰，牛斌，季文玉.客运专线铁路简支梁桥墩台纵向线刚度分析研究[J].铁道建筑，2010(4):21-25

[14] 徐浩，林红松，颜华.桥墩纵向水平刚度对简支梁桥桥上无缝线路的影响分析[J].铁道科学与工程学报，2016(5):871-875

[15] 中华人民共和国铁道部.TB10015—2012 铁路无缝线路设计规范[S].北京：中国铁道出版社，2013