气味干扰下带有避难所的食饵捕食者模型分析
申佩娴,薛亚奎
(中北大学 理学院, 太原 030051)

根据实验结论[10],只有当食饵感知到捕食者散发出的气味时才会减低其自身的繁殖率,造成种群整体数量的减少,进而影响捕食者种群的数量。假设捕食者只能捕食避难所之外的食饵,并且捕食者散发出的气味只对避难所之外的食饵的出生率造成影响,由此考虑避难所保护食饵的数量对模型的影响:当避难所保护食饵的数量逐渐增多时,会导致捕食者可捕食的食饵数量减少。本文用r0[1-cy]+刻画捕食者释放的气味对食饵出生率所造成的影响,其中把单个捕食者产生的气味干扰看做常数c,捕食者数量用y(t)表示。当气味干扰足够小或捕食者种群数量足够少时,避难所外食饵的出生率将不受捕食者气味影响;反之,食饵出生率将为0。由此建立如下模型:
(1)
其中:x(t)表示捕食种群数量;y(t)表示食饵种群数量;r0表示食饵的自然出生率;c表示气味对食饵出生率的干扰系数;mx(t)表示避难所保护的食饵数量;(1-m)x(t)表示能被捕食者能探测到的食饵数量;a表示食饵种群的密度制约系数;p表示捕食者的捕获率;u表示捕食者捕获食饵的转化率(u 假设m<1且c足够小,也就是说:避难所保护的食饵数量要少于食饵种群的总数量。由于气味对食饵种群的干扰系数依赖于捕食者种群的数量,因此只有气味干扰系数足够小时,避难所外的食饵才可以继续繁殖和生长。如果不满足以上条件,捕食者种群将会灭绝。因此,系统(1)变为: (2) 定理1 系统(2)的全部正解都是一致有界的。 证明定义一个关于解的和函数[11]z(t)=x(t)+y(t),则 -ax2+r0x-[p(1-m)-u(1-m)]xy-d1x-d2y≤x(-ax+r0)-mind1,d2}z (3) 所以总存在一个正数β1,使得式(3)变为 证明显然系统存在灭绝平衡点E0;若(T1)成立,即r0>d1,存在边界平衡点E1(x1,0)。 令系统(2)右端为零,即 (4) 由方程组(4)的第2个方程可得 (5) 将式(5)代入方程组(4)的第1个方程,可得 (6) 定理3 设:(T3)r0 1) 若(T3)成立,则E0局部渐近稳定;若(T1)成立,则E0不稳定。 2) 若(T1)、(T4)同时成立,则E1局部渐近稳定;若(T1)、(T2)同时成立,则E1不稳定;若(T5)成立,则E1是一个鞍结点。 3) 若(T1)、(T2)同时成立,则E2局部渐近稳定。 证明系统(2)在灭绝平衡点E0处的Jacobian矩阵为: 系统在平衡点E0处的特征方程为: λ2+(d2+d1-r0)λ+(d1-r0)d2=0 (7) 显然,λ1=-d2是方程(7)的一个根,若(T3)成立,则方程(7)的所有根均为负,E0局部渐近稳定;若(T1)成立,则方程(7)有一个正根,一个负根,故E0不稳定。 随着我国市场经济的发展,保险商业化的趋势不断加强。很多地区也开始试水医疗保险的商业化。如果医疗机构违反了医疗服务合同,给患者造成了人生伤害,可以通过购买商业保险的方式分散风险。现在的商业医疗保险的状况不容乐观,因为患者提出的高额损害赔偿常常令保险公司措手不及,使得很多商业保险公司放弃了医疗保险业务。但是如果我们可以把医疗服务合同的地位法定化,约定好双方当事人的权利和义务,这样商业保险公司理赔的时候才会有依据,商业医疗保险也会慢慢发展起来。医疗保险制度的构建,是一个“三赢”的局面,可以分散医疗机构的经营风险,扩大商业保险公司的业务范围,更有利于保护患者的利益。 系统(2)在边界平衡点E1处的Jacobian矩阵为: 则 故若(T1)、(T4)同时成立时,E1局部渐近稳定;若(T1)、(T2)同时成立时,E1不稳定。 (8) 系统(2)在正平衡点E2处的Jacobian矩阵为: 其中: a12=-r0cx*+r0cmx*-p(1-m)x* a21=u(1-m)y* a22=u(1-m)x*-d2 则: 其中: [r0-d1+u(1-m)]x-r0cyx(1-m)-ax2-p(1-m)xy-d2 证明令 F1(x,y)=r0mx+r0(1-cy)(1-m)x-p(1-m)xy -ax2-d1x F2(x,y)=u(1-m)xy-d2y 图1 系统(2)随避难所系数m及气味干扰系数c变化的轨线 从图1(d)和(e)可知:随着避难所系数m的增大,系统趋于稳定的时间延长,食饵种群和捕食种群的数量明显增加。从图1(f)可以看出:当避难所系数m足够大时,食饵数量将会大量增加,而捕食种群将趋于灭绝。因此,在一定的捕食者气味干扰下对食饵种群加入适当的避难所,不仅可以增加食饵种群的数量,同时也有利于捕食种群数量的增加。可见,气味干扰下对食饵种群加入避难所对捕食系统起着关键性的作用。 [1] CRESSMAN R.,GARAY J.A predator-prey refuge system:evolutionary stability in ecological systems[J].Theor.Popul.Biol,2009,76:248-257. [2] HUANG Y,CHEN F,ZHONG L.Stability analysis of prey-predator model with Holling type-III response function incorporating a prey refuge[J].Appl Math.Comput.2006,182:672-683. [3] MA Z H,WANG S F,LI W D,et al.The effect of prey refuge in a patchy predator-prey system[J].Mathematical Biosciences 2013,243:126-130. [4] MUKHERJEE D.The effect of prey refuges on a three species food chain model[J].Differential Equations Dynam.Systems,2014,22:413-426. [5] LV Y,YUAN R,PEI Y,et al.Two types of predator-prey models with harvesting:non-smooth and non-continuous[J].Comput Appl Math,2013,250(10):122-142. [6] SURACI J P,CLINCHY M,DILL L M,et al.Fear of large carnivores causes a trophic cascade[J].Nature communications,2016,73 (5):1-26. [7] ZHU Y,WANG K.Existence and global attractivity of positive periodic solutions for a predator-prey model with modified Leslie-Gower Holling-type II schemes[J].Math.Anal.Appl.2011,384:400-408. [8] PAL P J,SARWARDI S,SAHA T,et al.Mean square stability in a modified Leslie-Gower and holling-typeII predator-prey model[J].Appl.Math.Inform.,2011,29 (3/4):781-802. [9] LAI X,LIU S,LIN R.Rich dynamical behaviours for predator-prey model with weak Allee effect[J].Appl.Anal.,2010,8(89):1271-1292. [10] 王振龙,刘季科.艾鼬气味对根田鼠社会行为和繁殖的影响 [J].动物学报,2002,48(1):20-26. [11] GHOSH J,SAHOO B,PORIA S.Prey-predator dynamics with prey refuge providing additional food to predator[J].Chaos,Solitons and Fractals,2017,96:110-119. [12] SHAN C,ZHU H.Bifurcations and complex dynamics of an SIR model with the impact of the number of hospital beds [J].Journal of Differential Equations,2014,257(5):1662-1688. [13] 马知恩,周义仓.常微分方程定性与稳定性方法 [M].北京:科学出版社,2001. [14] SAHABUDDIN S,PRASHANTA K M,SANTANU R.Analysis of a competitive prey-predator system with a prey refuge[J].BioSystems,2012,110:133- 148. [15] DEBASIS M.The effect of refuge and immigration in a predator-prey system in the presence of a competitor for the prey[J].Nonlinear Analysis:Real World Applications 2016,31:277-287. [16] WANG X,ZANETTE L,ZOU X.Modelling the fear effect in predator-prey interactions[J].Journal of mathematical biology,2016,73(5):1179-1204.1 系统解的有界性

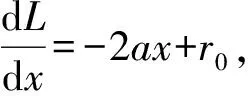
2 模型的分析
2.1 平衡点的存在性
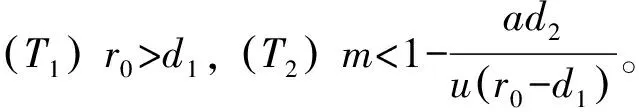
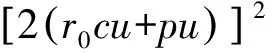
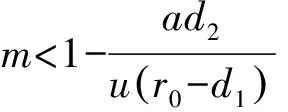
2.2 平衡点的局部稳定性




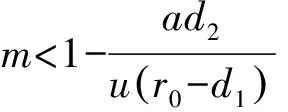
2.3 平衡点的全局稳定性
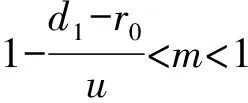
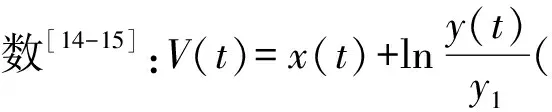
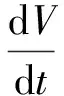
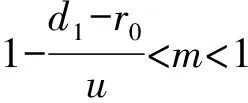
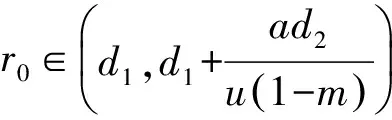
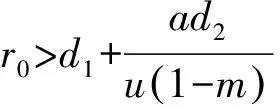
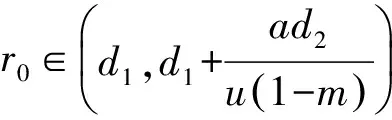
3 讨论


