天基物联网中一种非正交多载波调制技术

赵梦迪，李洪星，李 屹，方 莉，陈 萍

(1.北京邮电大学 信息与通信工程学院，北京 100876；2.上海航天电子技术研究所，上海 201109)

0 引言

随着通信技术和互联网技术的发展，物联网(Internet of Things，IoT)得到了广泛的支持和应用[1]。依托地面网络的物联网应用日趋发展成熟，但是在一些大范围、跨地域和恶劣环境等应用场景中，由于空间、环境等限制，地面物联网并不能满足数据交换需求[2]。尤其在海洋管理和船舶监测等领域，地面物联网还没有对其进行有力的支撑。因此，发展基于空间通信网络的天基物联网有其现实需求和广阔前景。然而，目前关于物联网的标准、技术和文献等主要是基于地面网络的陆基系统，天基物联网的相关研究才刚刚起步。将传统航天应用的卫星通信技术与新兴物联网、大数据技术进行跨界融合，对于实现人人相通、物物相通、人物相通的万物互联生态圈来说至关重要[3]。目前各国学术界和工业界都在积极考虑将天基网络和地基网络融合发展，使用户在室内、室外和野外等不同应用场景下，根据需求以4G、5G、WiFi和卫星等不同方式随时接入物联网信息服务系统，达到“有地用地、无地用天、天地一体”的良好用户体验[4]。

海事卫星通信系统可为用户提供速度、位置和时间等基本信息，具有全天时、全天候、全球覆盖和高精度等特点[5]，能有效支撑和补充地面系统，为船舶提供准确的时间信息、位置信息、导航和监控服务[6]。其中最引人关注的机器—机器(Machine-to-Machine，M2M)通信技术正在经历卫星通信市场的巨大增长。文献[7]分析了天地一体化信息网络的总体架构，文献[8-9]分析了卫星通信产业与物联网相融合的重要性和现实性，指出了卫星通信是天基物联网应用的重要组成部分。文献[10]分析了物联网的发展现状及趋势，针对其中提到的关于实现高速传输的问题，面向天基物联网的M2M通信系统可以采用多载波调制技术，但已有的多载波码分多址机制和正交频分复用技术并不适用。为了解决这一问题，本文提出一种基于非正交多载波调制的M2M通信方案，利用卫星信道作为天基物联网数据传输的方式，并采用16进制正交幅度调制方式对每路子载波进行调制，从而满足天基物联网大范围、长距离和高带宽的传输需求。

1 天基物联网

天基物联网体系如图1所示，主要包括3个层面：感知层、网络层和应用层[13]。

图1 天基物联网体系架构

天基物联网通过信息传感设备(如全球定位系统、激光扫描设备和传感器等)，把地面网络不能互联的物品与网络连接起来，进行信息通信和数据交换，从而实现对物品的定位、跟踪、监控和管理，最终达到物与物、人与物、人与人之间的互联互通互操作[11]。一般而言，天基物联网融合了天基导航、遥感和通信等服务，是一个无障碍交互的综合信息服务平台[12]。

卫星通信在物联网的3层体系中均起到了重要的支撑作用。在感知层，卫星定位终端、卫星数据采集终端等设备采集用户的位置、速度和运动时间等信息；在网络层，卫星通信网将采集到的信息进行可靠安全地传输；在应用层，经过卫星通信网络传输而来的有用信息成为各种应用平台信息资源的重要组成部分[6]。

2 非正交多载波调制技术设计

低轨道(Low Earth Orbit，LEO)卫星通信系统的多普勒效应会导致频偏产生，多普勒频移fd可按下式计算：

(1)

卫星轨道高度在500～2 000 km之间。船舶发送信号经过甚高频(Very High Frequency，VHF)海上移动频段进行传输，工作波段为161.975 MHz和162.025 MHz，根据波长公式λ=c/f，其中光速c=3×108m/s，频率f=162 MHz，估算出载波波长λ约为1.85 m。船速与卫星速度相比可忽略不计，因此卫星与用户的相对运动速度v的取值为24 807～27 371 km/h。

卫星与船舶之间的连线与卫星运行速度v方向之间的夹角θ为：

(2)

当θ=0°时，此时的多普勒频偏为最大多普勒频移：

(3)

由于LEO卫星移动通信系统会产生较大的多普勒频偏，不适合采用典型的多载波调制技术——正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)。因为OFDM技术最大的缺点是对频率偏移特别敏感，任何频率偏移都会破坏子载波间的正交性，这将不可避免地导致ICI。此外，OFDM时域信号的峰均比较高，调制信号的动态范围大，发射器增加了功放的成本，而且耗电量也大。因此，只能考虑非正交子载波调制机制。

为了实现卫星通信中的高速数据传输，有效地利用带宽，本文在100 kHz信道中采用16QAM对子载波信号进行调制。每一个符号包含4 bit，每路子载波的符号速率为2 400 symbol/s，相应的信息速率是9 600 bit/s。原始数据速率为307.2 kbps，采用32路非正交子载波，子载波频点为[14]：

fm=(0.5625-(M/2-m)×1.125)/T，

(4)

式中，M为子载波个数，m=0，1，2，…，M-1；T为子载波的符号周期，每个子载波中心频点的频率间隔Δf为2.7 kHz。容易看出，载波频点之间相互并不正交，正交的载波间隔Δf应为2.4 kHz。

非正交多载波调制系统如图2所示。

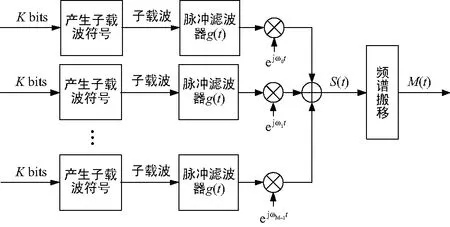
图2 多载波调制系统

已调信号的表达式为：

M(t)=Re{s(t)exp(j(2πfct+φ0))}，

(5)

式中，fc为载波频率；φ0为相位；s(t)为已调信号的复包络，即

(6)

式中，N为每个子载波一个时隙内传输的符号个数；Sm(n)为第m个子载波在时间tn处的调制符号；ωm=2πfm表示第m个子载波的角频率；g(t)为发送滤波器的冲击响应。

3 非正交多载波调制技术实现

3.1 方案实现

针对非正交的子载波，本文采用非正交多重调制(Non-orthogonal Multiple Modulation，NOMM)的思想[15]来实现多载波调制。

已知x是K维实随机矢量，y是其到L2(R)空间的线性映射，即

y=Gx，

(7)

式中，x为已知的K维实随机矢量，即x=[x0，x1，…，xK-1]T；G=[g0，g1，…，gK-1]，要求各列矢量线性无关但不一定满足正交性。在此系统中，y称为合成波，x称为信号矢量，xkgk称为子波[16]。

NOMM的信号点分布在以G各列矢量为基的K维星座图上，可先将G变换为标准正交基，如此，NOMM的星座图设计与传统调制方法就可以统一起来。

令R=GTG，则R是正定矩阵。于是存在K阶实矩阵P，使得

PRPT=I，

(8)

于是，GPT各列矢量就是标准正交基。至此，式(7)变为

y=GPTx。

(9)

接收端的解调器结构如图3所示。在相乘器中，输入矢量与P矩阵相乘。在判决器中进行判决即可。对于非正交矩阵G来说，在发送端和接收端分别用P进行线性变换，就可以有效消除不同符号之间的串扰或干扰。

图3 NOMM解调器结构

根据文献[17]中OFDM调制和解调的基本原理，串行比特流经过数据编码器后被映射为串行符号，每一个符号调制其中的一个子载波[18]。相对于非正交多载波技术，每个子载波都受到16QAM符号的调制，即16QAM等效基带信号的实部和虚部分别与相应非正交子载波的余弦分量和正弦分量相乘，调制后的各个子载波进行相加合成就构成了多载波符号[19]。

由上述的思路可知，式(7)中作为信号矢量的x，其行向量代表了串并变换后的一路16QAM信号，而G的列向量对应的是一路子载波频点。由于16QAM信号是复信号，含有实部和虚部，所以处理时把16QAM信号的实部和虚部分别提取出来，实部和子载波的cos(2πfmt)分量相乘，虚部和sin(2πfmt)分量相乘。这样就确定了G矩阵列向量的表现形式。

然而，由此会产生2个G矩阵，即由cos(2πfmt)频点分量组成的矩阵和由sin(2πfmt)频点分量组成的矩阵，须对这2个G矩阵进行合并。矩阵合并前，先确定时间t的取值范围。频点值最小的子载波的周期为T0=1/1350，符号周期为T=1/2400，容易算出每16个符号周期的时间段内，正好传了9个第一路子载波，3×9=27个第二路子载波。所以，每16个符号周期间可以看作是正交的。可见，t按照一个符号周期时间，也就是2 400(恰为16的整数倍)个符号时间取值是合理的。由此得到的R矩阵是对角阵，也就是正交的。

进一步，如果由cos(2πfmt)频点分量和sin(2πfmt)频点分量组成的2个G矩阵分别计算，得到相应的R矩阵和P矩阵。信号的实部和虚部再分别进行相应的调制，调制后的子载波再相加，在无噪声信道中传输仍无法实现无差错解调。这是因为对于第一路子载波而言，cos(2πf1t)和sin(2πf1t)在一个符号周期[0，T]内并不正交，这导致信号的实部和虚部对子载波分别进行调制再合成相加后会互相干扰。

因此，实部和虚部须进行联合调制解调。也就是说，2个G矩阵合并后，列向量的个数增加1倍，由原来的32增加到64。按照这个思路，可以令G矩阵的前32个列向量为cos(2πfmt)频点分量，其后32个列向量为sin(2πfmt)频点分量，即

(10)

这样一来，就确定了G矩阵的具体形式。相应地，信号矢量x的前32个行向量为16QAM信号的实部，后32个行向量为16QAM信号的虚部。进一步很容易计算出R矩阵和P矩阵，再进行调制和解调。如此，在无噪声信道中，接收端能够有效抑制子载波间干扰，实现无差错解调，进而保障天基物联网中的舰船之间(M2M)的高速数据交互。

3.2 仿真结果分析

利用计算机仿真来测试提出的实现方案的误比特率性能。在仿真中星座调制方式采用16QAM，共有32路子载波，子载波间隔为2.7 kHz，其中每个子载波受到16QAM符号的调制。每路子载波的符号速率为2 400 symbol/s，共仿真了100 s时间段内的数据量。调制后的多载波符号经过AWGN信道传输，信噪比取值范围为0 ～14 dB。

在未加噪声的情况下，对32路非正交子载波进行调制、解调和并串变换后的信号星座图如图4(a)所示。因为还未经过16QAM解调，所以星座图为16QAM星座图。显然，在没有噪声的信道中传输，尽管32路子载波非正交，但其非正交性并不影响系统的性能，这一点可以从图4(a)的星座图上直观地反映出来。因此，本文设计的方案能够有效消除子载波非正交性引起的子载波间干扰，从而获得正交时的性能。在加噪声的条件下，信噪比为10 dB时，对32路非正交子载波调制、解调和并串变换后的信号星座图如图4(b)所示。

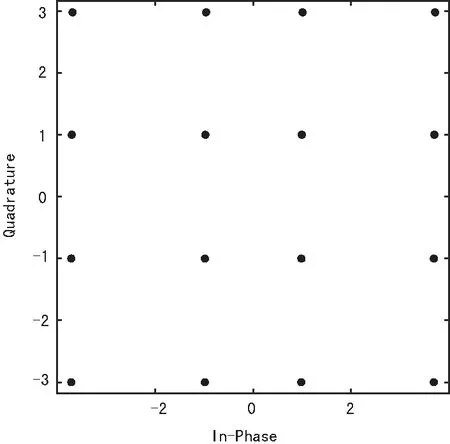
(a) 未加噪声时多载波解调后的星座图

(b) 信噪比为10 dB时多载波解调后的星座图图4 32路非正交多载波解调后的星座图

在数字卫星通信系统中，通常用Eb/N0来评估系统的性能。其中，Eb表示单位比特数据信号的能量，N0表示单位带宽内噪声的功率。非正交多载波系统的误比特率与Eb/N0的关系曲线以及与16QAM误比特率理论曲线的对比如图5所示。由图5可知，误比特率随着Eb/N0的增大而减小，并接近理论曲线，满足目标误比特率。

仿真结果表明，本文提出的机制能提高传输容量，提升系统性能，显示出了良好的性能特点。

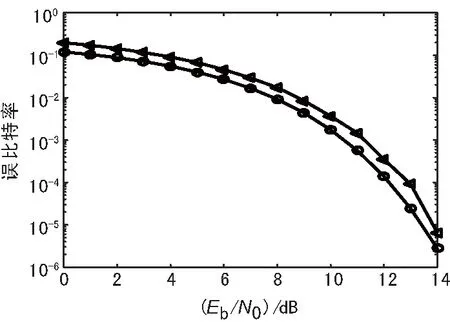
图5 误比特率性能

4 结束语

本文将传统卫星通信与物联网技术相结合，面向天基物联网应用，设计实现了100 kHz信道下一种新型的用于船舶间通信(M2M)的非正交多载波调制方案。该机制具有通信带宽大、通信覆盖范围广、通信可靠性高等特点，能够克服由于子载波间非正交性导致的ICI，达到目标误比特率。仿真结果验证了本文提出的非正交多载波实现方案具有一定的可用性和有效性。下一步的工作计划是将多载波调制技术与信道编码结合起来，进一步获得总体系统性能的提升。

[1] 曾业，周永将．天地一体化信息网络天基物联网应用体系研究[J]．现代导航，2016，7(5)：372-376．

[2] 柳罡，陆洲，周彬，等．天基物联网发展设想[J]．中国电子科学研究院学报，2015，10(6)：586-592．

[3] MINOLI D，SOHRABY K，OCCHIOGROSSO B.IoT Considerations，Requirements，and Architectures for Smart Buildings-energy Optimization and Next-generation Building Management Systems[J]．IEEE Internet of Things Journal，2017(4)：269-283．

[4] XU K，QU Y，YANG K．A Tutorial on the Internet of Things：From a Heterogeneous Network Integration Perspective [J]．IEEE Network，2016，30(2)：102-108．

[5] 杨宝军，王熹微，邵文峰．卫星应用助推物联网产业发展[J]．卫星应用，2010(5)：22-24．

[6] 闵士权．发挥卫星优势助推物联网发展[J]．国际太空，2012(1)：42-47．

[7] 吴曼青，吴巍，周彬，等．天地一体化信息网络总体架构设想[J]．卫星与网络，2016(3)：30-36．

[8] 吕子平，邓中亮．物联网及云计算时代的卫星通信[J]．国际天空，2013(1)：32-37．

[9] 赵杰颖，张政治，王龙．物联网时代的卫星导航产业[J]．数字通信世界，2011(2)：47-48．

[10] 东辉，唐景然，于东兴．物联网通信技术的发展现状及趋势综述[J]．通信技术，2014(11)：1233-1239．

[11] 赵凯，张峰．基于北斗卫星系统的物联网网络层体系架构设想[J]．计算机系统应用，2011，20(5)：6-8．

[12] 漆庄平．北斗卫星背景下物联网网络层体系架构分析[J]．科协论坛，2013(3)：67-68．

[13] 刘化君．物联网体系结构研究与讨论[J]．计算机与网络，2010，36(13)：68-71．

[14] EN 300 392-2 V3.2.1，Terrestrial Trunked Radio (TETRA)；Voice Plus Data (V+D)；Part2：Air Interface (AI) [S]．

[15] 孙山林．非正交多重调制的性能分析[J]．桂林航天工业学院学报，2013(1)：1-3．

[16] 曹祁生，梁德群．非正交多重调制的研究[J]．电子学报，2006，34(1)：19-23．

[17] 谭黎明．航空信道下的OFDM信号检测技术研究[D]．成都：电子科技大学，2014．

[18] 李向宁，谈振辉．OFDM基本原理及其在移动通信中的应用[J]．重庆邮电学院学报(自然科学版)，2003，15(2)：25-30．

[19] 韦涛，梁碧珍.OFDM通信系统中的频偏估计和抑制算法[J].移动通信，2017，41(16)：71-74.