基于滑动平均法的轨道交通短时客流实时预测

孟品超,李学源,贾洪飞,李延忠

(1.长春理工大学 理学院,长春130022;2.吉林大学 交通学院,长春130022;3.北华大学 数学与统计学院,吉林省吉林市132013)

0 引 言

轨道交通中滑动平均法模型简单易用,目前多用于对数据预处理,如裴益轩等[1]在实例应用中用滑动平均法给出了滤掉高频干扰信号的算法;胡松等[2]用滑动平均法滤波衰减了较高频率的噪声信号,达到提高信噪比的目的;何耀等[3]在所提出模型的基础上,采用滑动平均滤波法削弱噪声项干扰,起到了较好的估计效果。Hatchett等[4]鉴于较长移动平均效果差的状况,重新给出了移动平均最佳长度的建议。Shih等[5]将N点滑动平均的方法应用到普通示波血压确定过程,从而在可接受精确度范围内非常方便且无创地获得中枢主动脉收缩压值。

轨道交通客流具有周期性,每天客流波动具有一定规律性。客流时间序列在每天同一时间段客流量具有相似性,其构成的时间序列具有一定的平稳性。因此,可采用滑动平均法对历史客流数据在每天同一时间间隔内构成的时间序列进行建模,并采用滑动平均法[6]来一步预测相同时间间隔内的客流量。滑动平均模型简单,不需大量样本,且计算速度快,具有较高的预测精度。故本文提出了一种基于滑动平均法的轨道交通短时客流预测算法。

1 滑动平均法

1.1 基本算法

总体上波动较为平稳的离散时间序列{y t}可看成规律性成分的稳定性部分{f t}和受噪声因素影响的随机性波动{e t}两部分组成,故较为平稳的离散时间序列{y t}可分成两部分:

为减弱随机误差{e t}影响,通常可对总样本量为N的原始时间序列数据{y t}作滑动平均处理,即对非平稳的时间序列{y t},在合适的样本量为n的小区间上看作近似平稳的,其中n为滑动平均参数,然后在这个近似平稳的区间上采用式(2)进行平均处理,得到的值可以作为下一时刻的预测值。

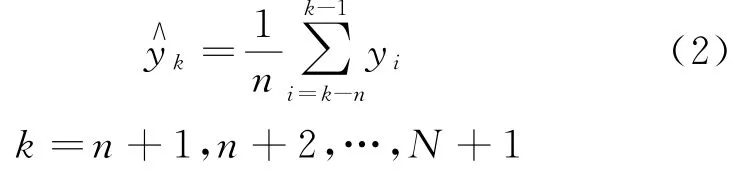
对于时间序列{y t}逐一对各小区间内数据进行局部平均化处理,得到减弱了噪声因素{e t}影响的预测时间序列。这样滑动平均所得到的},随机波动因受到平均的作用而比原时间序列{y t}减小了,也就是更加平滑了。

1.2 平均相对误差检验

针对预测算法的精度,Dhuyvetter and Kastens[7]采用平均绝对误差的方法衡量预测精度,Hatchett[8]考虑使用均方根误差来衡量预测精度,这两种衡量方法效果差别不大。本文拟采用消除量纲影响的平均相对误差来比较不同滑动参数下的预测误差。

取不同的滑动参数n就会有不同的滑动平均结果[9],滑动参数n过小,起不到抑制随机波动的作用;滑动平均参数n过大,越显均匀,但同时可能滤掉高频变化的规律性部分,导致总体预测精度不好。因此,应该选择一个较为合理的滑动参数n值来做滑动平均。选择较合理的滑动参数n的方法是,选取不同的滑动参数n值,计算不同n值对应的预测序列后,计算各自平均相对误差RME(n):

比较不同的RME(n),平均相对误差最小时所对应的滑动参数取值是合理的。RME(n)的值反映了取不同滑动参数时滑动平均预测的结果与历史数据的拟合程度,所以这种挑选方法是合理的。

2 基于滑动平均的短时客流实时预测

2.1 基于滑动平均法的短时客流实时预测

以每天为单位生成的原始客流时间序列受随机因素影响,波动强烈,呈现出明显的非平稳特征,但历史客流数据在每天同一时段内的数据具有相似性,其组成的时间序列起伏变化不会太大,可被视为变化较平稳的时间序列。所以,由历史客流时间序列每天同一时刻数据构成的时间序列,用滑动平均方法对下一天处于相同时间段数据进行预测,可得到基于历史数据的预测客流时间序列,接下来根据实时客流数据进行实时预测[10]。其方法简单、运算速度快,又具有较好的预测精度。具体算法步骤如下:

步骤1 生成原始客流时间序列矩阵。

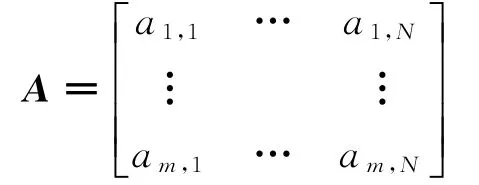
其中,N为每天生成的原始客流数据量,m为采集客流数据样本的天数。m天历史客流数据在每天同一时间段j的客流量所生成的新客流时间序列为:。

步骤2 确定用于滑动平均的参数n j。参数n j＝2,3,…,m－1,计算n j取不同值时的滑动结果:

不同的滑动参数n j所对应的预测平均相对误差为:

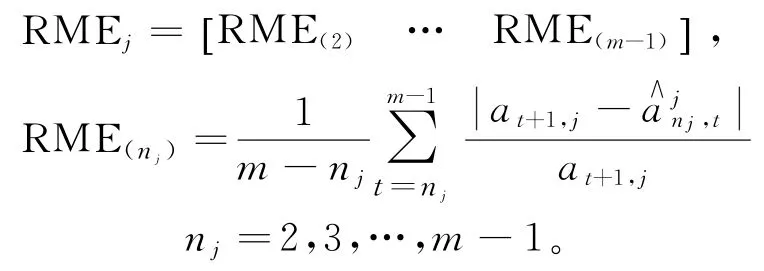
步骤3 采用滑动平均法预测第m＋1天各时刻的客流量数据。将取值最小时的滑动参数n j对应的作为第m＋1天时刻j的客流量预测值,同理,可以得到第m＋1天的预测客流时间序列:

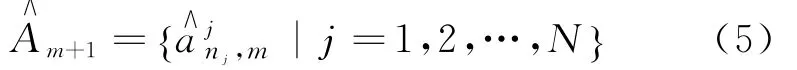
步骤4 基于实时客流数据对预测客流量进行实时预测。实时预测结果为:

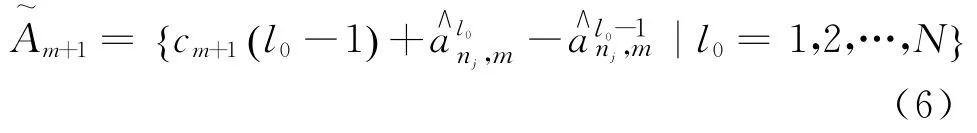
2.2 评价方法

本文拟采用平均相对误差(RME)和均方根误差(RMSE)这两种方法来对算法预测的误差效果进行评价[11]。

2.2.1 RME

平均相对误差用来评价预测客流数据与真实客流数据之间的相对误差的平均值,其计算公式为:

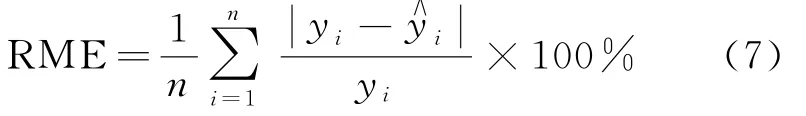
式中:y i为真实客流数据;为对应的预测客流数据;n为每天采样的客流数据量。

RME越接近于0,说明客流预测精确度越高。

2.2.2 RMSE

均方根误差用于评价预测客流数据与真实数据误差平方和的均值平方根,其公式如下:

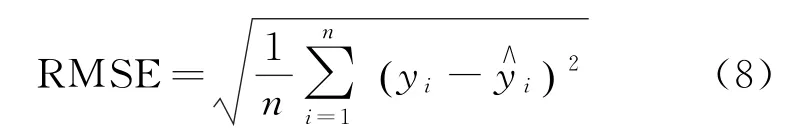
RMSE越接近于0,说明客流预测算法越准确。

3 实 验

基于本文提出的方法,针对2015年4月1日到29日上海地铁一号线人民广场站进站和莘庄站进站刷卡信息,分别采取5 min和15 min时间粒度采样生成原始客流时间序列。由于运营时间不同,5 min粒度时,人民广场站每一个完整运营日将获得212个进站观测值,莘庄站将获得204个进站观测值;15 min粒度时,人民广场站每一个完整运营日将获得70个进站观测值,莘庄站将获得68个进站观测值。共获得29天的原始客流数据。

实验首先通过最小平均相对误差检验方法确定滑动平均参数n j,然后用式(5)得出最小平均相对误差条件下第30天各时刻预测值。再根据实时客流数据用式(6)对预测结果处理,得到实时客流预测结果,并与支持向量机(SVM)、反向传播神经网络(BPNN)、小波神经网络(WNN)和小波组合支持向量机(WS)4种算法预测客流量误差进行比较。

3.1 人民广场地铁站进站客流预测

2015年4月1日人民广场地铁站进站客流经过5 min和15 min采样后得到客流时间序列如图1所示。图2为采用滑动平均方法预测4月30日5:45～5:50、6:00～6:15这两个时间段内客流量时,选取不同的滑动参数n j进行预测所对应的平均相对误差。基于实时交通客流数据,通过滑动平均方法,得到4月30日的5 min粒度和15 min粒度预测客流时间序列,其结果如图3所示。几种不同预测方法的实验误差见表1。

图1 2015年4月1日人民广场进站客流5 min和15 min粒度时间序列Fig.1 Entrance passenger flow time series with 5 min and 15 min at People’square station on April 1st,2015

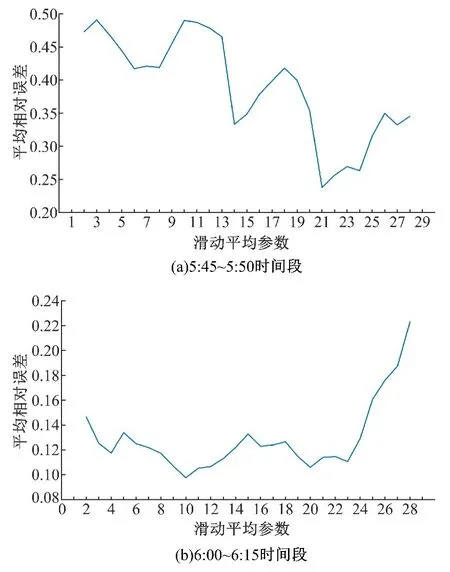
图2 预测不同时间段客流量时不同n j对应的RMEFig.2 RME corresponding to different n j while predicting the passenger flow between 5:45～5:50 and 6:00～6:15

图3 2015年4月30日人民广场站进站实时预测客流5 min和15 min粒度时间序列Fig.3 Real-time forecast of entrance passenger flow time series with 5 min and 15 min at People’square station on 30th April,2015

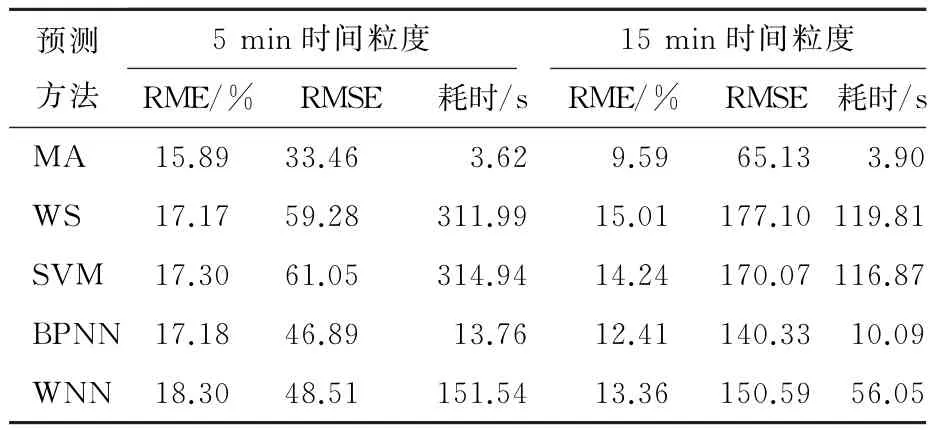
表1 2015年4月30日人民广场进站客流预测结果比较表Table 1 Comparison between predicted entrance passenger flows at People’s square station on April 30th,2015

通过表1对人民广场站进站短时客流预测结果分析可以发现,基于滑动平均法的实时客流预测精度最高,且计算耗时也远远少于其他方法。从图1和2可以看出,采取15 min粒度采样生成的原始客流时间序列更平滑,故预测15 min粒度的客流序列的平均相对误差更小。从图2可以看出,预测不同时间段的客流量所采用的滑动参数是依据预测RME最小标准自适应选取的。对比图3(a)(b)可知,在晚高峰时段客流数据波动强烈,导致拟合效果稍差。而本文提出的基于实时客流数据的滑动平均预测方法对晚高峰波动较强烈的数据具有较好预测效果。

3.2 莘庄地铁站进站客流预测

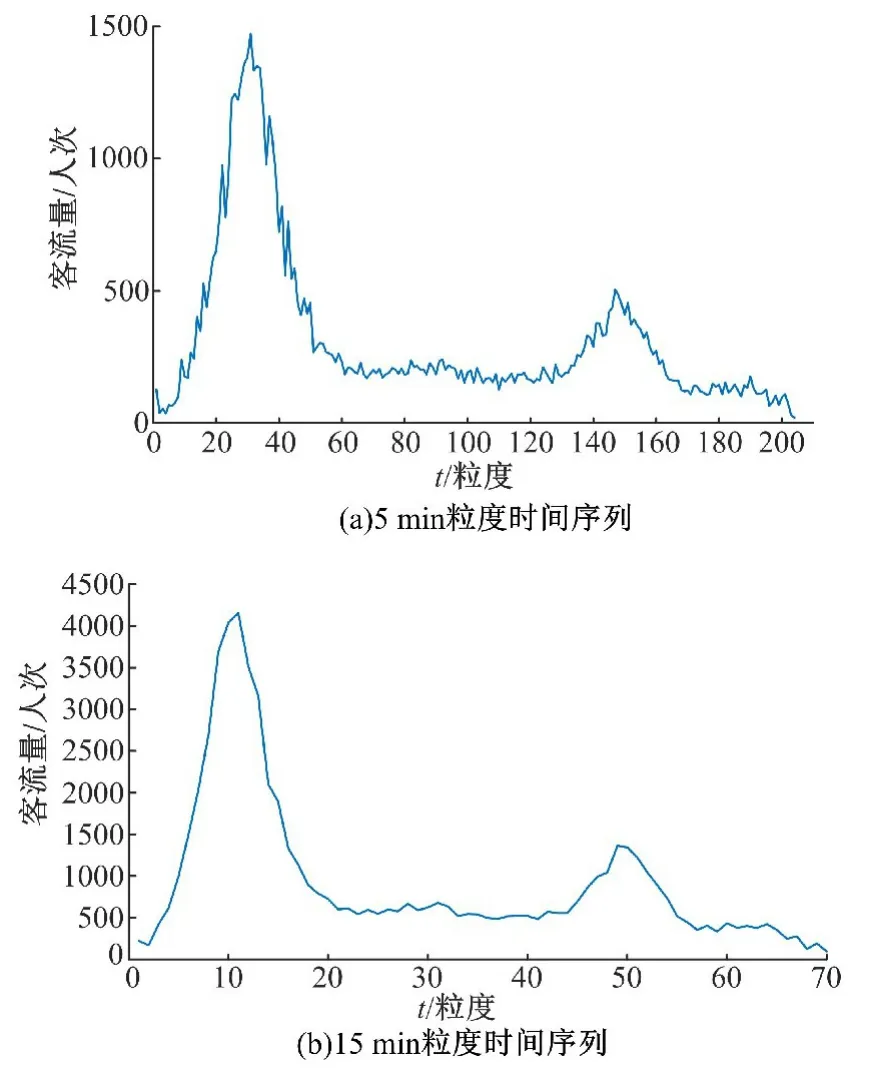
图4 2015年4月1日莘庄站进站客流5 min和15 min粒度时间序列Fig.4 Entrance passenger flow time series with 5 min and 15 min at Xinzhuang station on April 1st,2015

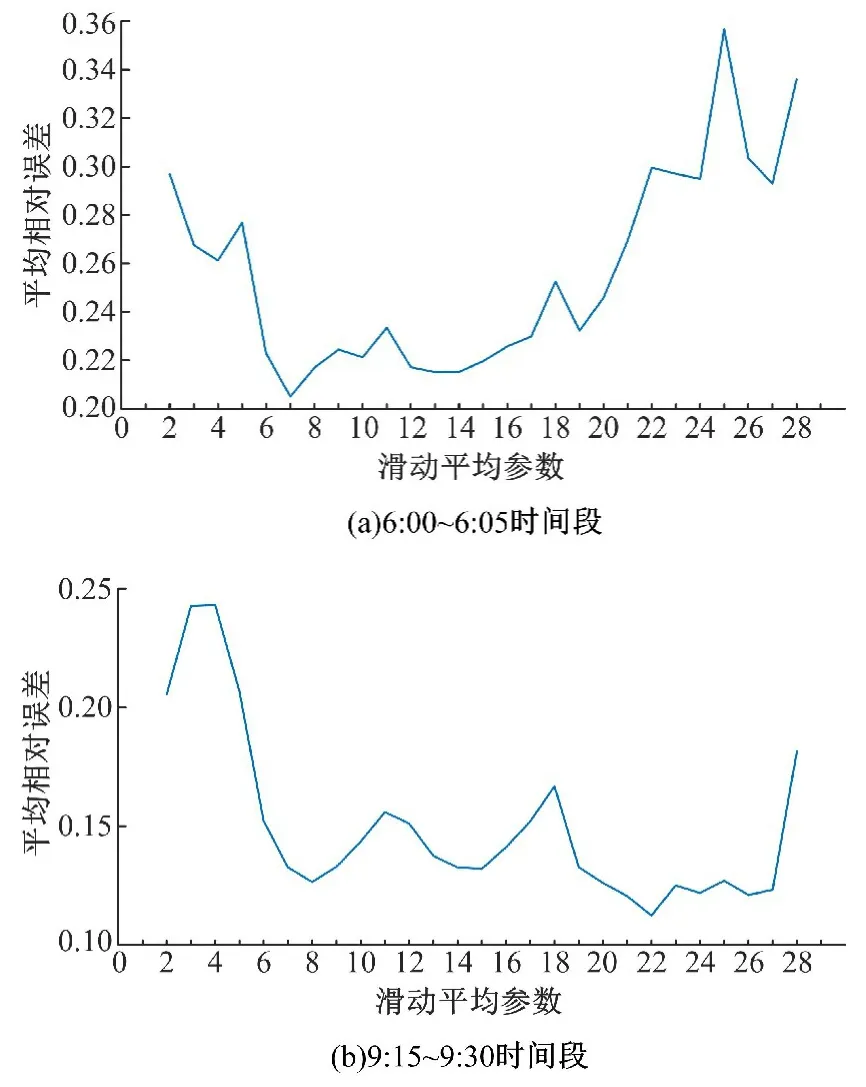
图5 预测不同时间段客流量时不同n j对应的RMEFig.5 RME corresponding to different n j while predicting passenger flow between 6:00～6:05 and 9:15～9:30

2015年4月1日上海市地铁一号线莘庄进站客流经5 min粒度和15 min粒度采样得到原始客流时间序列如图4所示。图5(a)(b)分别为采用滑动平均方法预测4月30日6:00～6:05、9:15～9:30这两个时段客流时,取不同滑动参数n j进行预测对应的平均相对误差。采用与实验1同样方法得到4月30日5 min粒度和15 min粒度预测客流时间序列如图6所示。几种不同方法的预测误差见表2。

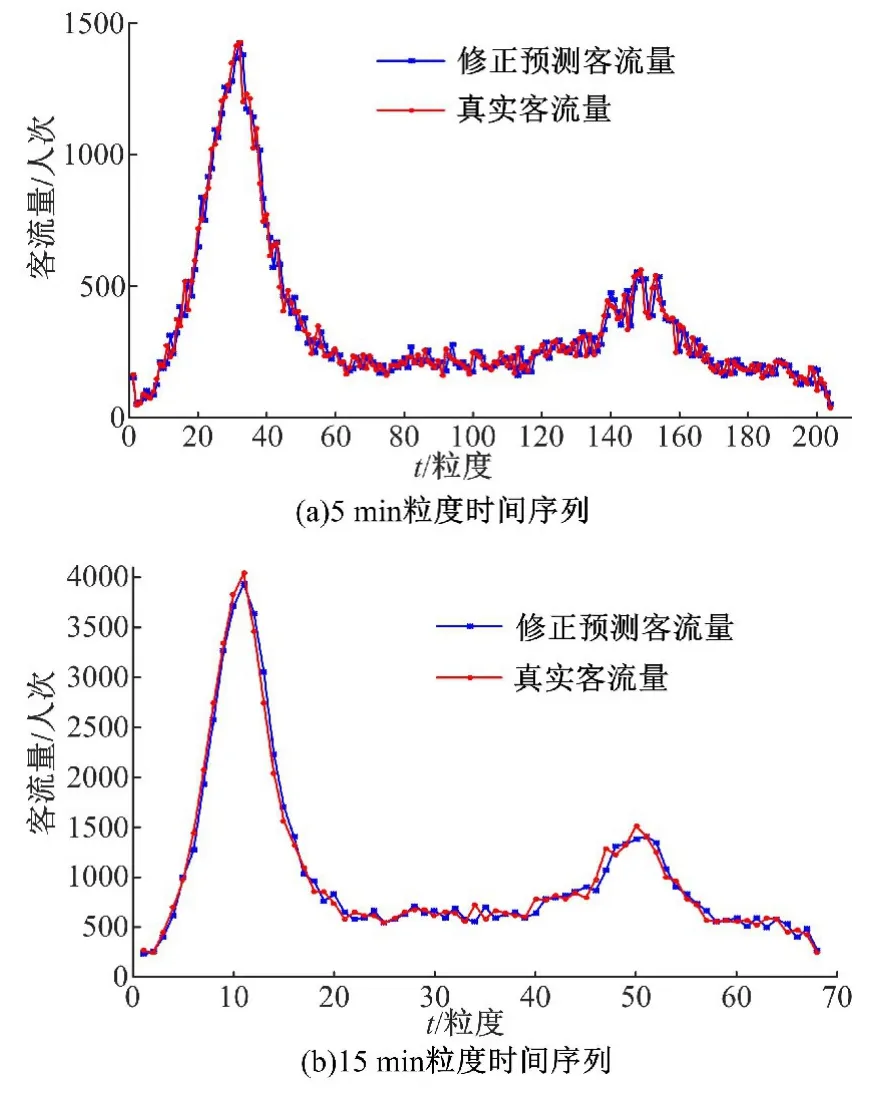
图6 2015年4月30日莘庄站进站实时预测客流5 min和15 min粒度时间序列Fig.6 Real-time forecast of entrance passenger flow time series with 5 min and 15 min at Xinzhuang station on 30th April,2015

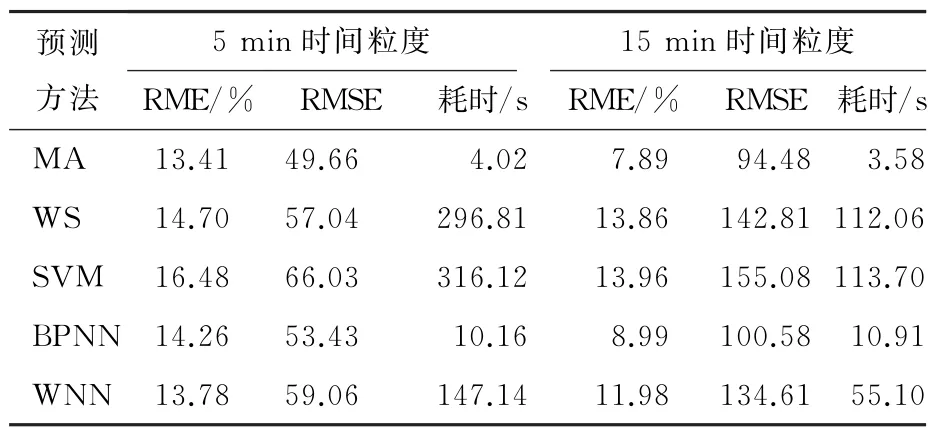
表2 2015年4月30日莘庄站进站客流预测结果比较表Table 2 Comparison between predicted entrance passenger flows at Xinzhuang Station on April 30th,2015

通过表2对莘庄站进站短时客流预测结果分析可以发现,基于实时交通客流的滑动平均预测方法精度高于其他4种预测方法,且运算时间优于其他方法。从图4可看出,15 min粒度采样生成的原始客流时间序列更平滑,波动性减弱,预测精度比5 min粒度的提高很多。对比图6(a)(b)可以发现,在波动强烈的早高峰时段,预测算法的拟合效果也较好,故本文提出的基于实时交通数据的滑动平均方法对早高峰客流数据也具有较好的预测效果。

4 结束语

针对轨道交通客流历史数据在每天相同时段内具有一定相似性的特点,以及当前应用于短时客流预测领域算法复杂、计算速度慢的不足,本文将算法简单、计算速度快的滑动平均方法应用于轨道交通短时客流领域。通过采用滑动平均算法对人民广场站和莘庄站两站点进站客流进行预测并验证。结果表明,本文提出的基于滑动平均算法的实时客流预测方法精度高于非线性预测方法支持向量机、BP神经网络和小波神经网络,也明显高于小波和支持向量机的组合预测方法。同时,滑动平均方法还具有算法简单、计算速度快的优点,具有较好的预测效果。

[1]裴益轩,郭民.滑动平均法的基本原理及应用[J].火炮发射与控制学报,2001(1):21-23.Pei Yi-xuan,Guo Min.The fundamental principle and application of sliding average method[J].Gun Launch&Control Journal,2001(1):21-23.

[2]胡松,江小炜,杨光,等.滑动平均滤波在微弱脉冲信号检测中的应用[J].计算机与数字工程,2007,35(10):169-172.Hu Song,Jiang Xiao-wei,Yang Guang,et al.Using of moving average filter in faint pulse signal detection[J].Computer and Digital Engineering,2007,35(10):169-172.

[3]何耀,刘兴涛,张陈斌,等.基于动力电池组内阻模型的绝缘检测算法[J].吉林大学学报:工学版,2013,43(5):1165-1170.He Yao,Liu Xing-tao,Zhang Chen-bin,et al.Insulation detection algorithm for high-power battery system based on internal resistance model[J].Journal of Jilin University(Engineering and Technology Edition),2013,43(5):1165-1170.

[4]Hatchett R B,Brorsen B W,Anderson K B.Optimal length of moving average to forecast futures basis[J].Journal of Agricultural and Resource Economics,2009,35(1):18-33.

[5]Shih Y T,Cheng H M,Sung S H,et al.Application of the N-Point moving average method for brachial pressure waveform-derived estimation of central aortic systolic pressure[J].Hypertension,2014,63(4):865-870.

[6]潘红宇.时间序列分析[M].北京:对外经济贸易大学出版社,2015.

[7]Dhuyvetter K C,Kastens T L.Forecasting crop basis:practical alternatives[C]∥Proceedings of the NCR-134 Conference on Applied Commodity Price Analysis,Forecasting,and Market Risk Management,Chicago,USA,1998:49-67.

[8]Hatchett R B.Optimal length of moving averages to use when forecasting basis[D].Stillwater Ok:Department of Agricultural Economics,Oklahoma State University,2009.

[9]杨林泉.预测与决策方法应用[M].北京:冶金工业出版社,2011.

[10]刘寒冰,李国恒,谭国金,等.基于时间序列的边坡位移实时预测方法[J].吉林大学学报:工学版,2012,42(增刊1):193-197.Liu Han-bing,Li Guo-heng,Tan Guo-jin,et al.Real-time prediction method of slop displacement based on time series analysis[J].Journal of Jilin University(Engineering and Technology Edition),2012,42(Sup.1):193-197.

[11]杨军.地铁客流短时预测及客流疏散模拟研究[D].北京:北京交通大学电子信息工程学院,2013.Yang Jun.Research on metro passenger flow shorttime prediction and evaluation simulation[D].Beijing:School of Electronic and Information Engineering,Beijing Jiaotong University,2013.