时间测度链上动力方程振动性的进展
杨甲山
(梧州学院 信息与电子工程学院,复杂系统仿真与智能计算实验室,广西 梧州 543002)
叙述了时间测度链上的基本概念及动力方程的基本理论以及动力方程振动性的最新进展,阐述了作者研究所得的一些最新成果,给出了应用实例,同时也提出了值得进一步研究的领域.
振动性; Emden-Fowler型动力方程; 时间测度链; 变时滞
众所周知,振动(也称振荡)是自然界和机械工程等技术领域中最普遍、最常见的一种物理现象,它广泛存在于物理学、生物种群动力学、自动控制技术等学科中的机械运动、电子电磁运动及原子运动等各种运动形式之中.无论在哪一种技术领域,还是在哪一种物理过程中,都会碰到各种形式、各种程度的振动过程.从自然界到工业各领域,从日常生活到社会领域,振动现象屡见不鲜.而振动现象往往通过方程的振动性表现出来.因此振动性是一种带有普遍意义的物质运动形式,是系统最重要的动力学性质之一.另一方面,在自然科学和社会科学的研究中,许多现象都可用泛函微分差分方程作为其数学模型,因此,对方程的定性理论(如振动性、稳定性、渐近性等)的研究不仅具有理论价值,而且具有实际意义.
既然时滞泛函差分方程是时滞泛函微分方程的离散形式,人们自然会问:经过差分化后的差分方程,其性质与原来的微分方程是否相同呢?许多研究表明,微分方程的许多性质经差分化后是保留下来了,但是,也有许多研究表明,微分方程与其相应的差分方程会有一些完全不同的性质. 例如,观察单个种群的生态数学模型的Logistic方程
x′(t)=rx(t)[1-k-1x(t)],r>0,k>0,
(1)
此方程的每一个解都是单调增加的. 但与其相应的离散系统——差分方程
Δx(n+1)=ax(n)[1-x(n)]
(2)
相比就会发现,当a=4时相应的差分方程(2)有一个混沌解,这就有了本质上的区别[1-2]. 另外,时滞泛函微分方程的振动性与相应的时滞泛函差分方程的振动性也会具有完全不同的特性. 例如,二阶常微分方程
x″(t)+a(t)f(x(t))=0
(3)
的某些振动性质与相应的二阶差分方程
Δ2x(n-1)+a(n)f(x(n))=0
(4)
的振动性质是不同的[3]. 另一方面,观察差分算子
(5)
和微分算子
(6)
发现它们的结构又十分类似. 这就启发科研工作者们:能否定义一个更一般的算子,它可以包括这两种特殊的算子呢?
德国学者StefanHilger[4]在其导师BerndAulbach指导下,于1990年首次提出了时间测度链(timescales,也称时间尺度、时标、时间轴、时间模等)的概念,并由此创建了时间测度链上动力系统(dynamicequationsontimescales)的理论. 之后, 这一新领域内有关问题(特别是时间测度链上动力方程的振动与非振动性、渐近性及稳定性等定性理论问题)的研究引起了国内外学术界的极大兴趣, 并发表了许多研究论文及专著[2-78].如Agarwal等[5-7]、Peterson等[8]、Sahiner[9]等给出了时间测度链上微积分的基本理论及时间测度链上的动力方程的诸多研究成果. 时间测度链T是实数域上的任意闭子集,当时间测度链T等于实数集或整数集时,时间测度链上动力方程的理论则分别表示微分方程和差分方程的经典理论. 时间测度链上动力方程的新理论不仅在生物种群动力学、量子力学、伺服力学、物理学(特别是量子理论及核物理等)、神经网络、自动控制技术、经济学和社会科学等领域中有非常重要的应用,而且还能解决许多不同领域里微分方程或差分方程不能解决的实际问题. 如Thomas和Peterson用时间测度链上的动力方程弥合了西尼罗河病毒传播的连续方面和离散方面之间的空隙[7-9].诸如物种种群的动态模型在季节上是离散的(并且遵循不同步长的动态模型差分方法或者经常被连续动态系统所仿效). 例如,在冬季当它们的卵处于孵化或休眠状态时,生物种群消失了,然而在接下来的新的季节里,孵化会产生不重复的种群[10]. 动力方程的新理论不仅在时间测度链上统一了微分方程和差分方程的有关理论,而且随着时间测度链的不同,将动力方程推广到了微分方程与差分方程之间. 在自然科学和社会科学的实践中, 许多有实际意义的时间测度链是存在的. 例如,当T=qN0={qt:t∈N0,q>1}时,这种情形的动力方程称为q-差分方程,这类方程在量子理论方面有重要的应用. 再例如当T=hN,T=N2={t2:t∈N}和时,它们可以应用于异于微分方程和差分方程的动力方程. 因此,时间测度链上的动力方程的振动理论、渐近理论等问题是微分方程学科的重要组成部分,它为解决自动控制技术、计算机科学、物理学(特别是核物理、量子理论方面等)、生物种群动力学、伺服力学、人口学、经济学以及神经网络等领域的实际问题提供了数学理论依据和科学基础. 所以,时间测度链上动力方程的振动与非振动等理论的研究既有重要的理论意义,更有广泛的应用前景.
论文将简单介绍动力方程振动性的一些最近的进展、作者的一些最新研究成果以及值得关注的领域.
1 一些基本概念
下面简单介绍一下有关时间测度链的一些基本概念及基本理论[5,8].
所谓时间测度链T, 就是实数域上的任意闭子集, 它仍然具有由诱导的拓扑以及中的顺序关系. 在时间测度链T上,记σ(t):=inf{s∈T:s>t},ρ(t):=sup{s∈T:s (7) 如果函数f在点t处连续,而点t是右稠密的,则其Δ-导数定义为 (8) 于是, 函数f(t)的Δ-导数fΔ、前跳算子σ与前跳距离μ之间有如下关系 fσ=f+μfΔ, (9) 其中:fσ=f°σ. 在时间测度链T上,两个函数的积及商的求导法则分别为 (fg)Δ(t)=fΔ(t)g(t)+f(σ(t))gΔ(t)=f(t)gΔ(t)+fΔ(t)g(σ(t)), (10) (11) 其中:ggσ≠0. 设a,b∈T,f为Δ-可微函数, 则fΔ的柯西(Cauchy)积分公式为 (12) 类似地,两类无穷限广义积分分别定义为 (13) 在时间测度链T上,分部积分公式(the integration by parts formula)为 (14) (15) 在时间测度链T上,n阶动力方程的一般形式为 f(t,x(t),xΔ(t),xΔ2(t),…,xΔn(t))=0,t∈T. (16) 在方程(16)中一定含有xΔn(t)这一项, 其中xΔ2(t),…,xΔn(t)分别称为二阶Δ-导数,…,n阶Δ-导数,并统称为高阶Δ-导数. 关于时间测度链上的更详细的理论及时间测度链上动力方程的基本理论,可参见文[5]或[8]. 动力方程虽然是最近发展起来的一个新的数学方向,其历史仅20余年, 但是, 由于它具有非常广泛的实际应用背景,并能解决一些用其他数学分支不能解决的问题,其发展也就变得异常迅速. 特别是近年来,时间测度链上动力方程的振动性的研究取得了丰硕成果[5-7,9-78], 且一阶动力方程的振动性理论已渐趋完善. 考虑时间测度链上如下一类非常广泛的具有非线性中立项的二阶非线性变时滞Emden-Fowler型阻尼动力方程 [A(t)φ1(yΔ(t))]Δ+b(t)φ1(yΔ(t))+P(t)F(φ2(x(δ(t))))=0,t∈T, (17) 其中:y(t)=x(t)+B(t)g(x(τ(t))),φ1(u)=|u|λ-1u,φ2(u)=|u|β-1u,λ>0,β>0为实常数;T为任意时间测度链,函数A(t),B(t),b(t),P(t)∈Crd(T,R),即A(t),B(t),b(t),P(t)均为定义在时间测度链T到实数域R上的实值rd-连续函数;τ(t),δ(t)均为定义在时间测度链T到T上的滞量函数;而函数g(u),F(u)∈C(R,R),并且满足ug(u)>0(u≠0),uF(u)>0(u≠0).并假设方程(17)中的有关函数满足下列条件: (H3)b(t)≥0;P(t)>0;A(t)>0且AΔ(t)≥0,并且-b/A∈R+. 方程(1)包含了大量的动力方程: 线性的、非线性的、无阻尼的、有阻尼的、无中立项的、有中立项的、常时滞的及变时滞的等,而其简单的特殊类型的动力方程的振动与非振动性及渐近性等,已出现了很多好的研究成果[6-7,9-78]. 如文[6]研究了时间测度链T上二阶时滞动力方程 xΔΔ(t)+p(t)x(τ(t))=0,t∈T, (18) 得到了方程(18)振动的若干充分条件. 而文[9,11]则研究了时间测度链T上二阶时滞动力方程 [r(t)xΔ(t)]Δ+p(t)f(x(τ(t)))=0,t∈T (19) 的振动性,得到了方程(19)若干新的振动准则,推广并改进了文[6]中的有关结果.文[12]则研究了时间测度链T上一类二阶常时滞泛函动力方程 {r(t)[(x(t)+p(t)x(t-τ))Δ]γ}Δ+f(t,x(t-δ))=0,t∈T, (20) 得到了方程(20)振动的一些充分条件.而文[13-15]则研究了时间测度链T上一类二阶变时滞的泛函动力方程 {r(t)[(x(t)+p(t)x(τ(t)))Δ]γ}Δ+f(t,x(δ(t)))=0,t∈T. (21) 利用广义的黎卡提(Riccati)变换及不等式技巧,得到了方程(21)振动的若干振动准则,推广、改进并丰富了已有的结果. 最近, 二阶Emden-Fowler型动力方程的振动性也出现了大量的研究成果. 如当T=R时的微分方程的情形,文[16-17]研究了二阶拟线性的Emden-Fowler型微分方程 [r(t)|x′(t)|α-1x′(t)]′+q(t)|x(t)|α-1x(t)=0,t≥t0 (22) 的振动性,给出了方程(22)若干振动准则. 文[18]则研究了一类更广泛的二阶拟线性的Emden-Fowler型变时滞微分方程 [r(t)|z′(t)|α-1z′(t)]′+f(t,x(σ(t)))=0,t≥t0 (23) 的振动性,得到了方程(23)振动的若干新的充分条件,方程中α>0是常数,函数z(t):=x(t)+p(t)x(τ(t)),f(t,x)sgnx≥q(t)|x|α(x≠0),q(t)>0且0≤p(t)≤p<1. 当T为任意时间测度链时,文[19]分别研究了2个Emden-Fowler型动力方程 [r(t)xΔ(t)]Δ+p(t)f(x(τ(t)))=0,t≥t0,t∈T (24) 和 [r(t)(xΔ(t))γ]Δ+p(t)xγ(t)=0,t≥t0,t∈T (25) 的振动性,并分别得到了上述2个方程(24)和(25)的一些振动性定理.这里要求常数γ>0是2个正奇数之商,并且rΔ(t)≥0.显然当γ>0是任意实数或者条件rΔ(t)≥0不满足,文[19]中的结果是不成立的.而文[20]研究了下列二阶Emden-Fowler型变时滞动力方程 [r(t)(xΔ(t))γ]Δ+p(t)xγ(τ(t))=0,t≥t0,t∈T (26) 的振动性,得到了方程(26)振动的若干判别定理,推广并改进了文[19]的一些结论,但同样γ>0是2个正奇数之商,且“σ(t)>t,ρ(t) [r(t)(xΔ(t))γ]Δ+f(t,x(g(t)))=0,t≥t0,t∈T, (27) 其中:函数|f(t,u)|≥q(t)|uγ|,得到了方程(27)若干振动性定理.但文[21]也要求γ≥1是2个正奇数之商,当γ是大于0的任意实数时其结果也是不成立的.紧接着,文[22]研究了一类更一般的二阶Emden-Fowler型变时滞动力方程 [p(t)(yΔ(t))γ]Δ+f(t,x(δ(t))=0,t≥t0,t∈T (28) 的振动性,方程中y(t):=x(t)+r(t)x(τ(t)),|f(t,u)|≥q(t)|uγ|,q(t)>0,得到了方程(28)振动的一些判别定理.但文[22]中同样也要求“γ≥1且τ∘δ=δ∘τ”,显然其结果当0<γ<1时也不成立.受到以上研究的启发,文[23-24]考虑了方程 (29) 在此基础上,文[25-27]研究了更一般的二阶Emden-Fowler型变时滞动力方程 {a(t)φ1([x(t)+p(t)g(x(τ(t)))]Δ)}Δ+q(t)f(φ2(x(δ(t))))=0,t∈T. (30) 上述方程中的函数φ1(u)=|u|α-1u,φ2(u)=|u|β-1u,而α>0和β>0均为实常数.显然这是Emden-Fowler型方程的更一般的情形,当α=β或者α=β且p(t)=0时就可得到上述各种类型的动力方程.作者利用时间测度链上的有关理论和广义Riccati变换技术及积分平均技巧,并借助时间测度链上的Hölder不等式,得到了方程(30)振动的一系列新准则, 其中一个最基本的结论为定理1. 定理1[25]如果存在一个正的单调非减且Δ可微的函数ξ(t),使得对充分大的T≥t0及δ(t)>G(T):=δ0,有 (31) 其中 (32) 显然,无论是α≥β还是α≤β,定理1都给出了方程(30)振动的判别定理.由定理1及其证明思想就可得到方程(30)许多其他类型的振动准则[25],这些结果改进、推广并丰富了现有的振动性结论.其他Emden-Fowler型动力方程的振动性研究成果可参看文[28-31]. 对于具有阻尼项的二阶Emden-Fowler型动力方程的振动性问题,文[32]率先研究了下列动力方程 [r(t)(xΔ(t))γ]Δ+p(t)(xΔσ(t))γ+q(t)f(x(τ(t)))=0,t∈T, (33) 在条件 (34) 成立下得到方程(33)的一些振动准则,推广并改进了已有的一些结果,其中 紧接着,文[33]研究了下列一类具有阻尼项的二阶拟线性动力方程 (a(t)|xΔ(t)|λ-1xΔ(t))Δ+b(t)|xΔ(t)|λ-1xΔ(t)+p(t)|x(δ(t))|λ-1x(δ(t))=0,t∈T, (35) 并得到方程(35)振动的一系列判别准则,结果之一为定理2. 定理2[33]假设 (36) 如果有一个正的可微函数φ:T→R,使得 (37) 则方程(35)在[t0,∞)T上是振动的. 这是文[33]的核心结果之一,也是方程(35)振动性最基本的判定定理,由此定理及其证明的基本思想,就可引导出方程(35)振动的一系列判定定理(如Kamenev型振动准则及Philos型振动准则等)[33-35].若条件(36)不成立,则有定理3. 定理3[33]假设 (38) 如果条件(37)成立, 并且 (39) 则在[t0,∞)T上方程(35)的每一个解x(t)或者振动或者收敛于0. 定理4[10]假设条件(38)成立, 并且 (40) 但另一方面,对于下列二阶Euler微分方程 (t2x′(t))′+q0x(t)=0. (41) 以上面这些研究为契机,文[40]再次讨论了方程(33)的振动性,得到了该方程的一个Philos型振动准则(由于此振动准则篇幅较长,故在此不作叙述),此振动准则虽然解决了二阶Euler微分方程(41)振动性的判别问题,但却要求γ≥1是2个正奇数之商,当γ是大于0的任意实数时其结果是不成立的,文[41]的结果亦是如此.根据以上研究成果,作者在文[42]中讨论了一类非常广泛的二阶阻尼动力方程(17)的振动性,主要结果为定理5. 定理5[42]设0≤B(t)<1且 (42) (43) 当λ>β时,有 (44) 这是文[42]的核心定理之一,由此定理及其证明的思路就可推出方程(17)的各种振动性定理(包括当条件(43)或(44)不成立时的振动准则)[42]. 显然,此定理解决了二阶Emden-Fowler型动力方程当λ≠β时的振动问题. 如果条件(42)不成立,就有定理6. (45) 如果存在函数φ∈C1(T,(0,∞)),使得当λ≤β时(43)式成立,当λ>β时(44)式成立,进一步,若 (46) 其中 (47) (48) (49) 则方程(17)在[t0,∞)T上是振动的. 以上定理5、6对两种情形的Euler微分方程(q0>0是常数) (50) 及方程(41)均能得到结果:当q0>1/4时方程是振动的. 其他类型方程振动的判别条件可参见文[44-47].当中立项的系数函数B(t)不满足条件0≤B(t)<1时,由于研究较为困难,这种情形方程(17)的振动性成果比较少,只有一些简单情形的振动准则[48-52].对方程(17),此时可引入一双广义的Riccati变换 (51) 及 (52) 通过对这一双Riccati变换进行仔细综合分析、研究和推导运算后,得到方程(17)振动的一个充分条件,即定理7. 定理7[53]设条件(42)成立,0≤B(t)≤b0<+∞,如果存在函数φ∈C1(T,(0,∞)),使得 (53) (54) 则方程(17)在[t0,∞)T上是振动的. 当条件(42)不满足而满足(45)时, 引入另一双广义的Riccati变换 (55) (56) 通过对这一双Riccati变换进行仔细综合分析、研究和推导运算后,得到方程(17)振动的一个充分条件,即定理8. 定理8[53]设条件(45)成立,0≤B(t)≤b0<+∞,如果存在函数φ∈C1(T,(0,∞)),使得(56)式与 (57) 同时函数 (58) (59) 则方程(17)在[t0,∞)T上是振动的. 由定理7、8及其证明思想,就可引导出方程(17)当0≤B(t)≤b0<+∞时振动的一系列判定定理(如Kamenev型振动准则及Philos型振动准则等)[53]. 同样,定理7、8对两种情形的Euler微分方程(50)及(41)均能得到结果:当q0>1/4时方程是振动的. 例1 考虑时间测度链T=[l,+∞)(l>1为常数)上的动力方程 (60) 其中:m=1,2,3,…,且 容易验证,定理5的所有条件都是满足的,于是由定理5知,方程(60)是振动的. 例2 考虑动力方程 (61) 其中:p0>0是常数. 可以验证,当p0>1/2时定理6的所有条件都是满足的,于是由定理6知,当p0>1/2时方程(61)是振动的. 例3 考虑动力方程 (62) 到目前为止,关于时间测度链上具有正负系数的动力方程振动性的研究仅有为数不多的几篇论文[54-57].在时间测度链上中立型动力方程中,当中立项的系数函数B(t)≤0时,其振动性成果不多,仅当-1 关于时间测度链上3阶或4阶动力方程的振动性,也出现了一定数量的研究论文[61-69],但总体成果却不是很多,而关于n阶动力方程的振动理论方面的论文就更少了[70-75].因此,从目前公开的关于3阶及3阶以上的高阶动力方程的研究成果来看,其动力学性质(如振动与非振动性、稳定性、渐近性等)既不完善也不成熟, 因此这类方程的定性理论也是值得挖掘的内容之一. 关于时间测度链上二维动力方程(即动力方程组)的有关动力学性质的研究目前也不多见[76-78],如文[76]研究了下列二维动力方程(t∈T) (63) 建立了二维动力方程(63)所有解振动的一些充分条件.目前,有关这类方程的定性理论的研究尚无多少进展,因此这类方程的定性理论也是值得探索的内容之一. 综上所述,时间测度链上的动力方程是一个较新的领域,也是有着广泛应用前景的应用数学分支,目前虽然出现一定数量的研究成果,并在一定程度上统一了相应的微分方程和差分方程的有关结论,但其整体理论还处在刚刚开始起步的萌芽阶段,其动力学性质如振动理论、渐近理论及其应用等问题的研究,仍然在深入探索之中,研究内容广泛且丰富,其理论和方法既不成熟也不完善,有待于进一步探索和研究,有许多未知的领域有待数学工作者去开拓,也有许多方法和问题等待我们去挖掘和解决,这些是值得数学工作者及自然科学和社会科学的有关研究工作者广泛关注的. [1] MAY R M. Simple mathematical models with very complicated dynamics[J]. Nature, 1976, 261 (10): 459-467. [2] 张炳根. 测度链上微分方程的进展[J]. 中国海洋大学学报 (自然科学版), 2004, 34 (5): 907-912. [3] ERBE L H, ZHANG B G. Oscillation of discrete analogues of delay equations[C]//In International Conference on Theory and Applications of Differential Equations, 1988: 21-25. [4] HILGER S. Analysis on measure chains-a unified approach to continuous and discrete calculus[J]. Results Math, 1990, 18: 18-56. [5] AGARWAL R P, BOHNER M, LI W T. Nonoscillation and oscillation: Theory for functional differential equations[M]. New York: Marcel Dekker, 2004. [6] AGARWAL R P, BOHNER M, SAKER S H. Oscillation of second order delay dynamic equations[J]. Canadian Applied Mathematics Quarterly, 2005, 13 (1): 1-18. [7] AGARWAL R P, BOHNER M, O′REGAN D, et al. Dynamic equations on time scales: a survey[J]. J Comput Appl Math, 2002, 141 (1/2): 1-26. [8] BOHNER M, PETERSON A. Dynamic equations on time scales, an introduction with applications[M]. Boston : Birkhauser, 2001. [9] SAHINER Y. Oscillation of second order delay differential equations on time scales[J]. Nonlinear Analysis, TMA, 2005, 63: 1073-1080. [10] ZHANG Q X. Oscillation of second-order half-linear delay dynamic equations with damping on time scales[J]. Journal of Computational and Applied Mathematics, 2011, 235: 1180-1188. [11] ERBE L, PETERSON A, SAKER S H. Oscillation criteria for second-order nonlinear delay dynamic equations[J]. J Math Anal Appl, 2007, 333: 505-522. [12] SAKER S H. Oscillation of second-order nonlinear neutral delay dynamic equations on time scales[J]. J Comput Appl Math, 2006, 187: 123-141. [13] WU H W, ZHUANG R K, MATHSEN R M. Oscillation criteria for second-order nonlinear neutral variable delay dynamic equations[J]. Appl Math Comput, 2006, 178: 321-331. [14] SAHINER Y. Oscillation of second-order neutral delay and mixed-type dynamic equations on time scales[J]. Adv Diff Eq, 2006: 1-9. [15] SAKER S H, AGARWAL R P, O’REGAN D. Oscillation results for second-order nonlinear neutral delay dynamic equations on time scales[J]. Applicable Analysis, 2007, 86: 1-17. [16] DZURINA J, STAVROUAKIS I P. Oscillation criteria for second order delay differential equations[J]. Appl Math Comput, 2003, 14 (3): 445-453. [17] SUN Y G, MENG F W. Note on the paper of dzurina and stavrouakis[J]. Appl Math Comput, 2006, 27 (4): 1634-1641. [18] JIU G D. Oscillation behavior of second order nonlinear neutral differential equations with deviating arguments[J]. Comput Math Appl, 2010, 59 (4): 3710-3717. [19] AGARWAL R P, BOHNER M, LI, ZHANG C. Oscillation criteria for second-order dynamic equations on time scales[J]. Applied Mathematics Letters, 2014, 31: 34-40. [20] TANG S, GAO C, LI T. Oscillation theorems for second-order quasi-linear delay dynamic equations[J]. Bull Malays Math Sci Soc, 2013, 36 (4): 907-916. [21] AGARWAL R P, ZHANG C, LI T. New Kamenev-type oscillation criteria for second-order nonlinear advanced dynamic equations[J]. Applied Mathematics and Computation, 2013, 225: 822-828. [22] LI T, SAKER S H. A note on oscillation criteria for second-order neutral dynamic equations on isolated time scales[J]. Commun Nonlinear Sci Numer Simulat, 2014, 19: 4185-4188. [23] 杨甲山. 时间轴上一类二阶动力系统的振动条件[J]. 中央民族大学学报 (自然科学版), 2017, 26 (2): 20-28. [24] 杨甲山, 莫协强. 时间轴上一类二阶动态系统振荡的充分条件[J]. 安徽大学学报 (自然科学版), 2014, 38 (5): 1-6. [25] 杨甲山, 谭伟明, 苏芳, 等. 时间模上二阶非线性中立型时滞泛函动态方程的振荡性[J]. 南开大学学报 (自然科学版), 2015, 48 (3): 24-31. [26] 于强, 杨甲山. 时间测度链上一类二阶非线性中立型泛函动态方程的振荡性[J]. 西北师范大学学报 (自然科学版), 2015, 51 (5): 12-17. [27] 杨甲山, 方彬. 时间模上一类二阶非线性中立型泛函动态方程的振荡性[J]. 内蒙古师范大学学报 (自然科学汉文版), 2016, 45 (5): 603-609. [28] ANDERSON D R, SAKER S H. Interval oscillation criteria for forced Emden-Fowler functional dynamic equations with oscillatory potential[J]. Sci China Math, 2013, 56: 561-576. [29] GÜVENILIR A F, NIZIGIYIMANA F. Oscillation criteria for second-order quasi-linear delay dynamic equations on time scales[J]. Advances in Difference Equations, 2014, 2: 45-54. [30] SHI Y, HAN Z, SUN Y. Oscillation criteria for a generalized Emden-Fowler dynamic equation on time scales[J]. Advances in Difference Equations, 2016, 2: 63-71. [31] BOHNER M, HASSAN T S, LI T. Fite-Hille-Wintner-type oscillation criteria for second-order half-linear dynamic equations with deviating arguments[DB/OL]. [2017-01-03]. https: //doi. org/10. 1016/j. indag. 2017. 10. 006. [32] ERBE L, HASSAN T S, PETERSON A. Oscillation criteria for nonlinear damped dynamic equations on time scales[J]. Appl Math Comput, 2008, 203: 343-357. [33] 张全信, 高丽. 时间尺度上具阻尼项的二阶半线性时滞动力方程的振动准则[J]. 中国科学: 数学, 2010, 40 (7): 673-682. [34] 张全信, 高丽, 刘守华. 时间尺度上具阻尼项的二阶半线性时滞动力方程的振动准则 (II)[J]. 中国科学: 数学, 2011, 41 (10): 885-896. [35] 张全信, 高丽, 刘守华. 时间尺度上具阻尼项的二阶半线性时滞动力方程振动性的新结果[J]. 中国科学: 数学, 2013, 43 (8): 793-806. [36] 孙一冰, 韩振来, 孙书荣, 等. 时间尺度上一类二阶具阻尼项的半线性中立型时滞动力方程的振动性[J]. 应用数学学报, 2013, 36 (3): 480-494. [37] YANG J S, QIN X W, ZHANG X J. Oscillation criteria for certain second-order nonlinear neutral delay dynamic equations with damping on time scales[J]. Mathematica Applicata, 2015, 28 (2): 439-448. [38] YANG J S, QIN X W. Oscillation criteria for certain second-order Emden-Fowler delay functional dynamic equations with damping on time scales[J]. Advances in Difference Equations, 2015, 2 (1): 97-113. [39] 杨甲山, 方彬. 时间测度链上一类二阶非线性时滞阻尼动力方程的振动性分析[J]. 应用数学, 2017, 30 (1): 16-26. [40] BOHNER M, LI T. Kamenev-type criteria for nonlinear damped dynamic equations[J]. Sci China Math, 2015, 58: 1445-1452. [41] AGARWAL R P, BOHNER M, LI T. Oscillatory behavior of second-order half-linear damped dynamic equations[J]. Applied Mathematics and Computation, 2015, 254: 408-418. [42] 杨甲山. 时间测度链上一类二阶Emden-Fowler型动态方程的振荡性[J]. 应用数学学报, 2016, 39 (3): 334-350. [43] 杨甲山. 时间测度链上二阶Emden-Fowler型动态方程的振动性[J]. 吉林大学学报 (理学版), 2017, 55 (1): 12-16. [44] YANG J S. Oscillation of second-order nonlinear dynamic equation on time scales[J]. Chinese Quarterly Journal of Mathematics, 2013, 28 (2): 172-179. [45] YANG J S, SU F. Oscillation criteria for certain second-order nonlinear dynamic equations with damping[J]. Mathematica Applicata, 2014, 27 (2): 392-404. [46] 杨甲山. 时标上一类具阻尼项的二阶动态方程的振荡性[J]. 系统科学与数学, 2014, 34 (6): 734-751. [47] YANG J S, QIN X W, ZHANG X J. Oscillation criteria for certain second-order nonlinear neutral delay dynamic equations with damping on time scales[J]. Mathematica Applicata, 2015, 28 (2): 439-448. [48] HAN Z, LI T, SUN S, et al. On the oscillation of second-order neutral delay dynamic equations on time scales[J]. African Diaspora Journal of Mathematics, 2010, 9 (1): 76-86. [49] ZHANG C, AGARWAL R P, BOHNER M, et al. New oscillation results for second-order neutral delay dynamic equations[J]. Advances in Difference Equations, 2012, 4: 22-27. [50] 杨甲山, 莫协强. 时间模上一类二阶非线性动态方程的振动结果[J]. 安徽大学学报 (自然科学版), 2015, 39 (1): 1-7. [51] 杨甲山, 谭伟明, 覃学文, 等. 时间模上二阶非线性阻尼动力方程的振动性分析[J]. 浙江大学学报 (理学版), 2016, 43 (1): 64-70. [52] 杨甲山, 张晓建. 时间模上一类二阶非线性动态方程振荡性的新结果[J]. 华东师范大学学报 (自然科学版), 2017 (3): 54-63. [53] 杨甲山, 李同兴. 时间模上一类二阶阻尼Emden-Fowler型动态方程的振荡性[J]. 数学物理学报, 2017, 37 (6): 993-1015. [54] CHEN D X, QU P X, LAN Y H. Oscillation of second-order nonlinear dynamic equations with positive and negative coefficients[J]. Advances in Difference Equations, 2013, 3: 168-175. [55] 杨甲山. 时间测度链上具正负系数的二阶阻尼动力方程的振动准则[J]. 数学物理学报, 2014, 34A (2): 393- 408. [56] DENG X H, WANG Q R, AGARWAL R P. Oscillation and nonoscillation for second order neutral dynamic equations with positive and negative coefficients on time scales[J]. Advances in Difference Equations, 2014, 2: 1-7. [57] DENG X H, WANG Q R, ZHOU Z. Oscillation criteria for second order neutral dynamic equations of Emden-Fowler type with positive and negative coefficients on time scales[J]. Sci China Math, 2017, 60: 113-132. [58] 孙书荣, 韩振来, 张承慧. 时间尺度上二阶Emden-Fowler中立型时滞动力方程的振动准则[J]. 上海交通大学学报 (自然科学版), 2008, 42 (12): 2070-2073. [59] SUN Y, HAN Z, LI T, et al. Oscillation criteria for second-order quasilinear neutral delay dynamic equations on time scales[J]. Advances in Difference Equations, 2010, 22: 51-63. [60] BOHNER M, LI T. Oscillation of second-orderp-Laplace dynamic equations with a nonpositive neutral coefficient[J]. Applied Mathematics Letters, 2014, 37: 72-76. [61] QIU Y C, ZADA A, QIN H, et al. Oscillation criteria for nonlinear third-order neutral dynamic equations with damping on time scales[J]. Journal of Function Spaces, 2017, 32: 80-89. [62] LI T, ZHANG C. Properties of third-order half-linear dynamic equations with an unbounded neutral coefficient[J]. Advances in Difference Equations, 2013, 4: 33-41. [63] YANG J S. Oscillation criteria for certain third-order variable delay functional dynamic equations on time scales[J]. Journal of Applied Mathematics and Computing, 2013, 43 (1/2): 445-466. [64] CANDAN T. Asymptotic properties of solutions of third-order nonlinear neutral dynamic equations[J]. Advances in Difference Equations, 2014, 1: 35-43. [65] QIU Y C. Oscillation criteria of third-order nonlinear dynamic equations with nonpositive neutral coefficients on time scales[J]. Advances in Difference Equations, 2015, 2: 29-38. [66] QIU Y C. On nonoscillatory solutions tending to zero of third-order nonlinear dynamic equations on time scales[J]. Advances in Difference Equations, 2016, 1: 10-18. [67] QIUA Y C, ZADA A, TANGC S, et al. Existence of nonoscillatory solutions to nonlinear third-order neutral dynamic equations on time scales[J]. J Nonlinear Sci Appl, 2017, 10: 4352-4363. [68] MOAAZ O, ELABBASY E M, BAZIGHIFAN O. On the asymptotic behavior of fourth-order functional differential equations[J]. Advances in Difference Equations, 2017, 2: 26-37. [69] ZHANG C H, AGARWAL R P, BOHNER M, et al. Oscillation of fourth-order delay dynamic equations[J]. Sci China Math, 2015, 58: 143-160. [70] WU X, SUN T, XI H, et al. Kamenev-type oscillation criteria for higher-order nonlinear dynamic equations on time scales[J]. Advances in Difference Equations, 2013, 2: 24-33. [71] YANG J S. Oscillation fornth-order nonlinear neutral delay dynamic equations on time scales[J]. Mathematica Applicata, 2013, 26 (4): 816-827. [72] SUN T, YU W, HE Q. New oscillation criteria for higher order delay dynamic equations on time scales[J]. Advances in Difference Equations, 2014, 4: 32-41. [73] TAO C, SUN T, XI H. Existence of the nonoscillatory solutions of higher order neutral dynamic equations on time scales[J]. Advances in Difference Equations, 2015, 2: 27-35. [74] TAO C, SUN T, HE Q. Nonoscillation for higher-order nonlinear delay dynamic equations on time scales[J]. Advances in Difference Equations, 2016, 1: 58-66. [75] HASSAN T S. Asymptotics and oscillation of higher-order functional dynamic equations with Laplacian and deviating arguments[J]. Advances in Difference Equations, 2017, 2: 14-26. [76] Xu Y, Xu Z. Oscillation criteria for two-dimensional dynamic systems on time scales[J]. Journal of Computational and Applied Mathematics, 2009, 22: 59-69. [77] XU Z T, XIE H H. Oscillation of certain two-dimensional dynamic system[J]. Chinese Journal of Engineering Mathematics, 2013, 30 (5): 756-760. [78] YU J C, DENG L H. Oscillation criteria for two-dimensional dynamic systems with variable delay on time scales[J]. Mathematica Applicata, 2013, 26 (4): 839-845.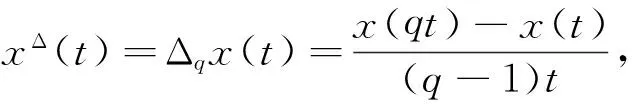
2 二阶动力方程的振动性进展









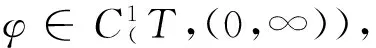
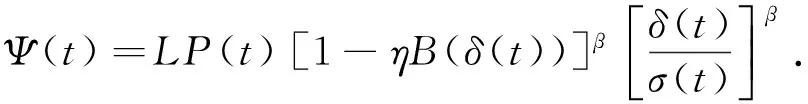




3 其他动力方程的振动性进展

