引入WFCM算法能提高信用违约测度模型准确率吗？

熊正德　张帆　熊一鹏

摘 要：选取沪深A股上市的制造业公司财务变量构建信用风险评价体系，在利用因子分析法对其进行维数约简后，采用数据挖掘技术和统计学方法对信用违约概率测度作了有价值的探索。模型包含两个阶段，聚类阶段采用加权模糊C均值聚类（WFCM）算法将样本聚成同质的类，使同簇样本更具代表性；违约测度阶段应用Logistic回归方法分别对不同组样本进行测度。实证结果表明：在Logistic模型中引入WFCM算法能显著提高预测样本的违约概率测度准确率；对于样本总体与ST企业而言，其违约预测准确率比Logistic模型分别提高了10.7%和20%；ROC检验结果也说明WFCM.Logistic模型具有更强适用性。

关键词： 违约预测；加权模糊C均值聚類；Logistic模型；信用评级

中图分类号：F064.1 文献标识码： A 文章编号：1003.7217（2018）01.0147.07

一、引 言

上市公司作为各自行业领域内实力雄厚且盈利能力较好的企业，已日益成为商业银行所青睐的贷款对象。截至2015年底，境内上市公司数目达到2，827家，总市值规模达到531，304亿元①，上市公司在数量与规模上均实现了很大发展；与此同时，我国银行业不良贷款余额已达12，613亿元②，不良贷款规模呈不断增长趋势。商业银行之间竞争加剧、上市公司持续强劲的信贷需求，不断增加的杠杆扩大了企业受财务风险冲击的可能性，银行业资产质量的脆弱性也不断增加，不良贷款规模持续增长已严重阻碍了国民经济健康发展。为实现对贷款客户的授信以及有效的贷后管理，提高信用违约概率测度准确率以及降低第I类错误风险成为金融业孜孜不倦的追求。正如West等所说，预测模型每提高1%的准确率，都足以为金融业节省巨大成本[1]。

早期对信用违约概率大小的判断主要依靠信贷专家个人经验，传统的专家判断法由于主观性太强及判断标准不一致，逐渐不适用于复杂的信用市场。此后，随着数理统计和计算机技术快速发展，量化模型被引入到信用风险管理领域，现代信用风险模型也逐渐过渡到以数据为驱动、以数学模型和统计计量方法为基础的量化模型时代。

企业信用风险量化模型主要分为计量模型和人工智能模型。计量模型主要包含ZETA评分、Logistic模型、KMV等，人工智能模型主要包含神经网络、支持向量机和聚类分析等。国内外众多学者对各类模型的适用性、准确性进行了比较研究，如Lee和Sung采用神经网络和Logistic模型对韩国信用违约账户进行预测，发现Logistic模型具有更强稳定性，更适合对违约风险进行分析[2]。李志辉和李萌利用在银行有过贷款的上市公司财务信息和违约数据分别构建线性判别模型和Logistic模型，实证结果表明Logistic模型是较为理想的信用风险识别模型[3]。韩岗在对国外主流信用风险测度模型进行比较研究后，结合我国国情，指出Logistic模型其拟合度较高、适用性较强[4]。张洪祥和毛志忠利用模糊聚类方法对上市公司信用风险进行评价，证实该方法具有良好的评价效果及实用价值[5]。刘祥东和王未卿对贝叶斯判别方法、Logistic模型和BP神经网络模型在信用风险中的识别能力进行比较，发现贝叶斯判别法和Logistic模型可识别重要财务变量、有效解释公司财务状况，而BP神经网络则缺乏对信用风险识别结果解释能力[6]。上述学者通过比较研究发现Logistic模型风险识别能力强、预测精度较高且可有效解释公司财务状况，以Logistic模型作为企业信用违约概率测度模型具有较强适用性。

然而Logistic回归模型也有其不容忽视的局限性，该模型第I类错误率较高，且无法分析不同企业之间违约因素的差异性。针对单一模型由于自身固有缺陷可能影响风险识别准确率的问题，学者们尝试通过构建混合模型来进一步提高风险识别准确率。学者Hush和Gopalakrishnan等[7-8]先后证明聚类分析是一种计算简便且较为精确的分类方法，其分类结果更为稳健。Yu等通过对混合模型与单一模型的对比研究，指出通过不同分类模型的组合能够比使用单一分类模型实现更高精确度[9]。Tsai和Chen对四种混合方式进行研究发现，基于聚类和分类相结合的混合模型可以提供更高的预测精度[10]。马海英[11]通过混合神经网络和Logistic回归分析发现混合模型的预测精度比单独使用神经网络模型和Logistic回归的预测精度高。De等以2007年西班牙破产企业与非破产企业作为样本，通过利用模糊C均值聚类（FCM）和多元自适应回归样条法构造混合模型，并与判别分析，多元自适应样条法以及前馈神经网络进行比较分析，研究结果表明，混合模型的准确率优于单一模型[12]。

综上，本文选取具有较强适用性的Logistic回归模型作为企业信用违约概率测度模型，并试图构建混合模型来解决其固有局限对预测精度的影响。同时，在参考弗兰克·奈特和Hu等相关研究结论[13，14]的基础上，本文在违约概率测度前引入FCM算法对样本进行聚类处理，通过模糊聚类将具有相似风险特征的样本进行归组，以提高同簇样本数据的代表性，探索不同组企业间的违约风险差异性特征以提高违约风险整体识别准确率。此外，学者Yuan等通过研究发现属性特征的重要性程度对分类结果有显著影响，提出了基于属性加权策略的FCM算法[15]。因此，考虑到不同风险评价变量在违约重要性程度上的差异，本文对传统的FCM算法做了风险加权校正，使得聚类结果更符合信用风险识别要求。

二、WFCM.Logistic混合模型设计

通过上文对模型的比较分析发现，Logistic模型具有风险识别能力强、预测精度较高且可有效解释公司财务状况等优点。然而，在实际应用中，为对信用风险进行准确评估，信贷审批人员一般会尽量多地收集贷款人的大量相关信息，尤其是企业相关财务数据，从而使解释变量的估计系数可靠性降低，进而导致违约概率测度结果不准确。Logistic模型一般采用逐步回归方法对变量加以筛选，这就造成对违约有显著影响的部分变量信息丢失情况，回归方程估计结果不准确，没有考虑变量之间相互影响的问题。endprint

为此，相关学者通过对信用违约风险变量进行因子分析得到主成分因子，将其作为自变量纳入Logistic模型中，以解决模型存在信息丢失的问题。相对Logistic模型而言，基于因子分析的Logistic模型在尽可能保留原始数据信息的条件下，减少了模型中的变量数目，避免由于多重共线性问题对违约测度结果的影响，提高了回归系数的可靠性，使得信用违约概率测度的结果更加准确可靠。然而，该模型缺乏对不同企业违约差异的有效识别。从非系统性风险特点来看，企业的违约具有个体差异性特征，因子分析Logistic模型并不能深度挖掘不同企业违约因素的个体差异。

受Tsai和Chen的研究[10]启发，本文提出一种将模糊聚类和Logistic分类相结合的WFCM.Logistic混合模型，该模型能有效识别不同企业违约差异性特征，提高违约预测精度。首先，对选取的变量进行因子分析，以避免共线性问题对后续聚类和分类结果产生影响；其次，利用WFCM算法，将样本进行聚类处理，使同簇样本带有某种规律性特征，不同簇样本之间则呈现某种较大差异；最后，对不同簇样本分别建立Logistic回归模型。WFCM.Logistic模型通过利用数据挖掘聚类分析技术对主成分因子进行风险归组，有助于提高同簇样本的代表性，进而利用Logistic分析方法识别不同簇样本的违约关键因素，提高违约概率测度准确率。此外，它能帮助商业银行等机构多角度、多层面了解不同簇企业之间的违约差异，并找到具有相似风险特征贷款企业。

三、信用违约风险评价体系构建

（一）样本选取

目前，我国债券市场只有少数几家企业出现债券违约情况，也难以从银行内部得到企业贷款的相关数据信息。因此，本文参照国内众多学者对上市公司违约的研究成果，将被ST处理的企业视为违约样本，非ST企业视为正常样本。为排除行业因素对预测结果的影响，本文选择在沪深A股上市的制造业公司为样本，选取2016年中国A股市场因财务状况异常而被特别处理的制造业上市公司作为违约样本。在剔除数据残缺及数据异常的ST公司样本后，最终得到45家ST企业作为研究样本。按照“主营业务相同、企业规模大体相当”原则，ST企业与非ST企业按1：5进行配比，选取同年度的正常企业作为ST公司配对样本，最终得到267家上市企业数据，其中ST企业45家，非ST企业199家③。并将其中40家ST企业以及与之配对的199家非ST企业作为建模的样本数据，剩下的5家ST企业以及23家非ST企业作为测试集。

中国证券市场以连续两年亏损或每股净资产低于股票面值为标准对上市公司财务状况异常进行ST处理，能否在前3年对企业的风险状况做准确预测显得尤为重要。所以，本文选用ST公司在被“戴帽”之前第三年的数据，即如果某ST公司2016年被宣布特别处理，则选取该公司2013年数据，且与之配对的正常公司也选择2013年数据。

（二）变量的筛选

财务变量能比较综合地反映上市企业一定时期内财务状况变化，准确地揭示企业盈利质量，与其它资产存在方式相比更容易核查与验证，且现金流变量受企业经营者主观歪曲的可能性较小。因此，以上市企业财务数据作为自变量能较好地解释企业的信用违约风险。

本文所选取的财务变量主要涉及企业获利、偿债、发展、运营等方面能力，以及现金流状况、股东获利情况和财务杠杆比率。这类财务变量能较好反映企业的经营状况及盈利能力等内容，进而反映企业信用违约风险的大小。

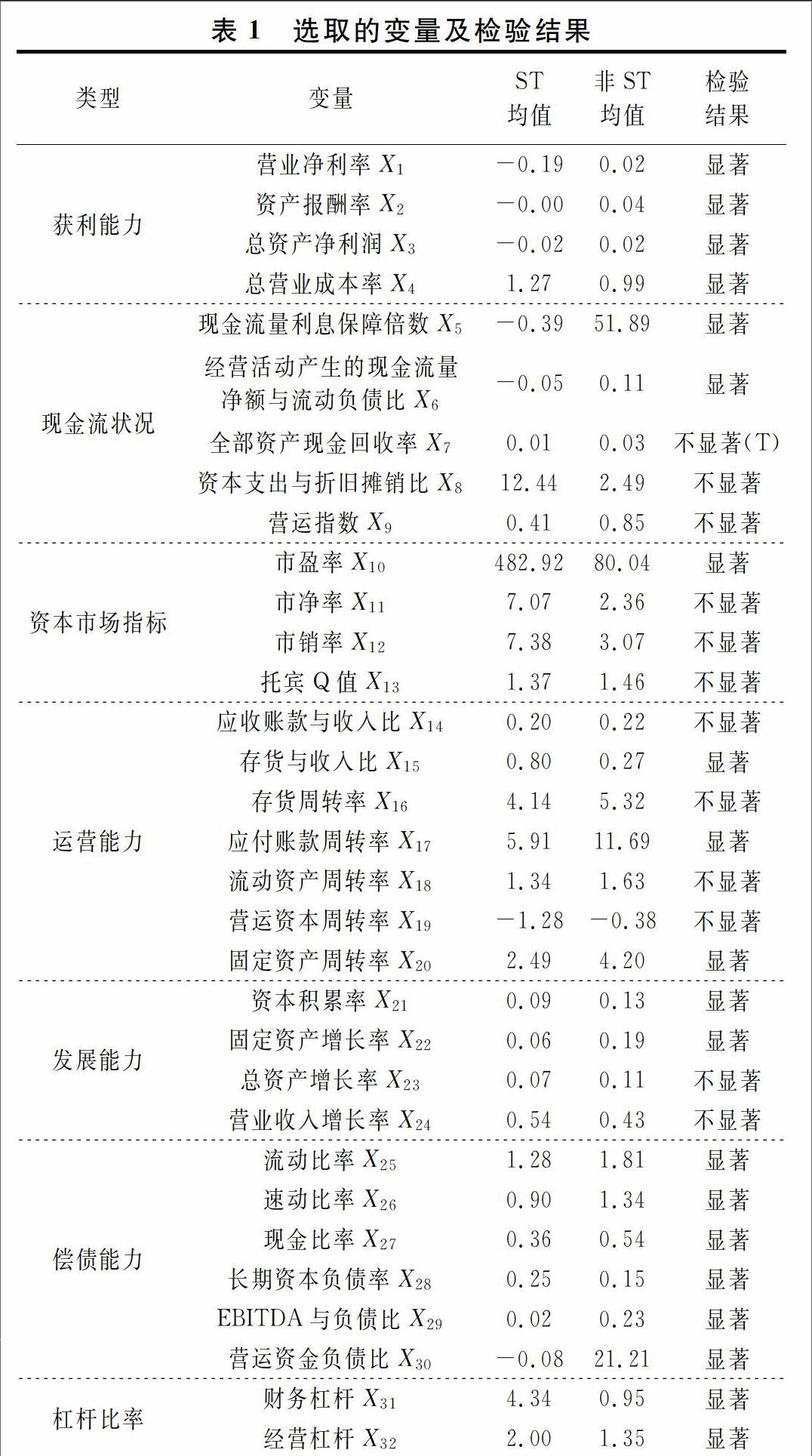
在参考李志辉[3]、张洪祥[5]和朱卫东[16]等人对财务变量体系的研究基础上，本文评价体系构建依据科学性、整体性、独立性、可行性的原则，选择32个财务变量作为备选评价变量。为使变量体系更加简化，有效筛选出风险识别能力较强的变量，避免变量过多带来多重共线性问题，本文使用K.S检验对变量分布进行正态性检验，对服从正态分布的变量用样本独立T检验进行区分度显著性检验，对不服从正态分布的变量用Mann.Whiteney方法进行区分度显著性检验。变量选取与检验结果如表1所示。

表1中，（T）表示K.S检验结果符合正态分布使用独立样本T检验进行区分度显著性检验结果；检验结果未标注部分表示K.S检验结果不符合正态分布使用Mann.Whitney检验进行区分度显著性检验结果。通过显著性检验，本文选取营业净利率、资产报酬率等20个对违约有显著性影响的指标作为后续模型构建的自变量。

四、实证研究

通过对变量进行描述性统计分析发现，各变量的统计量之间存在较大差距，导致这种差距的原因是由于变量尺度或量纲不同，这会影响后续模型的拟合效果，故有必要对数据进行标准化处理。虽然在变量违约相关性检验过程中剔除了部分不显著的变量，但通过对变量做两两之间的Pearson相关性分析发现，部分变量之间存在着较强的相关性，直接将所有变量纳入回归模型不仅冗杂，且可能会出现多重共线性致使结果失真。因此，需要对变量进行因子分析处理以减少模型受变量多重共线性的影响。

（一）主成分分析

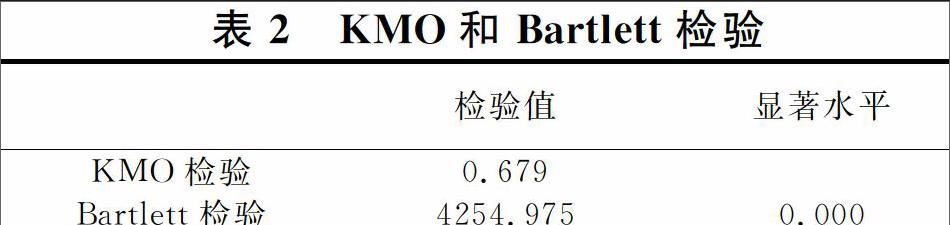
在进行主成分分析前，需要对数据进行相关检验，以判断能否对数据做降维处理。检验的主要方法是KMO检验和Bartlett球形度检验，其检验结果如表2所示。

从表2的检验结果来看，KMO检验值大于0.6和Bartlett球形度检验P值为0，说明表1中通过Mann.Whiteney检验和T检验筛选出的20个变量适合进行因子分析。

使用SPSS对变量进行因子分析，以特征值大于或等于1为因子选取标准，根据因子解释的总方差来看，因子Z1～Z8的累积方差贡献率达到74.623%，提供了足够的原始数据信息，能反映较大部分的方差变化情况，因子分析结果较为理想。

表3是各因子系數矩阵，因子Z1、Z5主要反映企业盈利能力，因子Z2、Z6主要反映企业偿债能力，因子Z3、Z4主要反映企业运营能力，因子Z7、Z8主要反映企业的经营风险大小。endprint

（二）WFCM.Logistic分析

1.WFCM聚类结果分析。通过向商业银行信贷专家进行问卷调查，并对各因子进行比较后，运用层次分析法得到各因子权重为：w=[0.2408，2084，0.1265，0.0914，0.1016，0.0623，0.0710，0.0925]。

本文通过运用Matlab 2012a编写了WFCM及其有效性检验代码，对数据进行多次聚类迭代处理。为判别分类结果数目，提高分类评价结果准确性，本文借鉴Zhang等[20]提出了FCM有效性指数，该指数在计算过程中将类内与类间的相似性相结合，进而对样本分类结果进行选择。其中，Var表示类内样本的集中程度之和，该指标越小类内的紧致度越好；Sep表示模糊集群两两之间的分离度之和，该指标越大表示类与类之间划分效果越好；V值是结合Var和Sep的综合评价结果，该值越小说明聚类的整体效果越好。其分类有效性评价指标详见表4。

从表4结果来看，最优的聚类结果是将样本进行4分类，但考虑到样本量的大小以及Logistic回归对样本量的要求，本文选择将样本进行2分类，第一类（C1）与第二类（C2）的聚类结果如表5所示。

表6给出了Logistic回归模型的估算结果，模型1（M1）和模型2（M2）是指经过WFCM算法处理后再分别进行Logistic回归的拟合结果，模型3（M3）则是直接将所有样本进行Logistic回归的拟合结果。SPSS还给出了反映模型整体拟合优度的检验指标-2LL、CSR2和NR2。-2LL取值越小说明模型拟合效果越好，CSR2和NR2取值越大模型拟合效果越好。从表6拟合优度检验值可以看出，模型1和模型2的拟合优度检验结果均优于模型3，表明经过聚类处理后的Logistic回归模型具有更好的拟合度。

表6还给出了Logistic回归模型中各因子回归结果，其中回归系数大于零，表示违约率与该因子之间呈正相关关系，反之则呈负相关关系。从回归结果系数来看，Z1、Z2和Z5三个因子的系数都显著为负，表明偿债能力因子和盈利能力因子可以作为判断企业是否会发生违约的重要变量，且盈利能力因子在违约风险测度中更为重要。从模型1与模型2来看，Z3、Z4和Z6三个因子存在显著性差异，表明经过聚类分析处理后，Logistic模型能更好识别出不同簇企业的关键风险因子。此外，因子Z5主要反映企业的发展潜力，企业的发展潜力越大其信用风险则相对较小，其数值大小应与企业的信用违约概率负相关。而从模型3来看，Logistic回归模型中因子Z5的系数值显然与实际情况不符。可以看出，Logistic模型对违约因素缺乏解释力，对样本进行聚类再回归是可行且有效的，能更好地解释违约的关键因子。

3.模型判别能力分析。

为更好地验证WFCM.Logistic模型是否能提高违约预测准确率及降低模型犯第I类错误的概率，本文用相同样本对比分析了Logistic模型（M3）与WFCM.Logistic模型的违约预测准确率。

由表7可以看出，相比Logistic模型而言，WFCM.Logistic模型对总体的违约预测准确率由82.4%提高到了85.8%，第I类错误率由82.5%下降到67.5%，第Ⅱ类错误率由4.5%下降到3.5%。对于每类样本而言，第I类错误率均有所降低。说明WFCM.Logistic模型在提高整体违约预测准确率的同时能较好地识别出违约企业。

4.模型的ROC比较分析。

为检验模型违约概率测度结果的准确性，运用ROC方法对比分析了Logistic模型和WFCM.Logistic模型所预测的违约概率值，模型预测准确性的度量用ROC曲线下的面积即AUC值表示，其结果如图1与表8。

ROC曲线反映的是当违约阈值不断变化时，模型违约预测结果准确性的动态变化情况。ROC曲线距离左上方越近，则说明分类器效果越好。从图1来看，相比Logistic模型而言，通过引入WFCM聚类算法，能较好地提高Logistic模型的违约预测精度。

由表8可以看出，WFCM.Logistic模型的AUC值为0.837， Logistic模型的AUC值为0.815，说明当违约阈值动态变化时，WFCM.Logistic模型分类器效果较好，其违约概率测度准确率较高，具有更强适用性。

（三）模型预测性检验

1.预测准确性检验。通过计算测试集样本与聚类中心的贴近度，将测试集样本分别归入不同类，从而计算出各样本的违约概率。上述训练样本的聚类簇中心如表9所示。

本文利用加权欧式距离方法计算测试集样本与簇中心的距离，通过比较样本分别离P1和P2距离大小，将测试集样本分为不同的类。根据贴近度计算结果，第一类有2个预测样本，第二类有27个预测样本。将被分类好的样本分别纳入所属类的Logistic回归模型中并与Logistic模型进行比较，其预测结果如表10和表11所示。

由表10和表11可以看出，WFCM.Logistic模型的预测效果明显优于Logistic模型。其中，模型总体预测准确度提高10.7%，第Ⅰ类、第Ⅱ类错误率分别降低20%、8.7%。因此，通过WFCM方法对预测样本进行分类处理后代入Logistic回归模型中能有效提高Logistic模型预测结果的准确度。

2.ROC比较分析。

将WFCM.Logistic模型与Logistic模型的样本违约概率结果进行ROC比较，其结果如图2所示。

从预测样本的ROC曲线图可以看出，相比较Logistic模型而言，隨着违约阈值的变化，引入WFCM算法的Logistic模型具有更好的违约预测准确率。可以认为，基于WFCM算法的两阶段模型具有更加精确的违约概率测度结果，其违约预测准确率也更高。endprint

五、结 论

本文将WFCM算法引入到企业信用违约概率测度模型中来，以我国制造业上市公司的经验数据对企业信用违约风险进行实证分析，通过比较分析WFCM.Logistic模型与Logistic模型的违约测度结果，得出以下结论：

第一，在训练样本与预测样本中，无论是针对违约客户还是正常客户的预测效果而言，WFCM.Logistic模型均优于Logistic模型； ROC检验结果也表明，引入WFCM算法后，Logistic模型具有更高的预测准确度，其对违约概率测度的结果也更具适用性。

第二，在Logistic模型中引入WFCM算法对训练样本进行分类再回归发现，不同簇之间的违约显著性因子存在差异，引入WFCM算法有助于对不同企业违约风险进行差异化计量与风险管理。

第三，与Logistic模型相比，WFCM.Logistic模型对风险因子的解释能力更强，其适用性也更强。本研究从企业违约的差异性特征角度出发，通过构建差异化的企业信用违约风险评估模型，能有效提高Logistic模型的预警效果。

注释：

①中国银行业监督管理委员会（http：//www.pbc.gov.cn）。

② 国泰安数据库（http：//www.gtarsc.com）。

③ 因少部分ST企业配对样本较少，本文非ST企业配对实际数量低于预估值。

参考文献：

[1] West D， Dellana S， Qian J. Neural network ensemble strategies for financial decision applications[J]. Computers & Operations Research， 2005， 32（10）：2543-2559.

[2] Lee T H， Sung.Chang J. Forecasting creditworthiness： Logistic vs. artificial neural net[J]. Journal of Business Forecasting Methods and Systems， 2000， 18（4）： 28-30.

[3] 李志輝， 李萌. 我国商业银行信用风险识别模型及其实证研究[J]. 广东社会科学， 2005，27（5）：17-22.

[4] 韩岗. 国外信用风险度量方法及其适用性研究[J]. 国际金融研究，2008（3）：43-47.

[5] 张洪祥，毛志忠. 基于多维时间序列的灰色模糊信用评价研究[J]. 管理科学学报，2011，14（1）：28-37.

[6] 刘祥东，王未卿. 我国商业银行信用风险识别的多模型比较研究[J]. 经济经纬，2015，32（6）：132-137.

[7] Hush D R， Horne B G. Progress in supervised neural networks[J]. Signal Processing Magazine，1993， 10（1）：8-39.

[8] Gopalakrishnan M， Sridhar V， Krishnamurthy H. Some applications of clustering in the design of neural networks[J]. Pattern Recognition Letters， 1995， 16（1）：59-65.

[9] Yu L， Wang S， Lai K K. Credit risk assessment with a multistage neural network ensemble learning approach[J]. Expert Systems with Applications， 2008， 34（2）：1434-1444.

[10]Tsai C F， Chen M L. Credit rating by hybrid machine learning techniques[J]. Applied Soft Computing， 2010， 10（2）： 374-380.

[11]马海英. 基于神经网络及Logistic回归的混合信用卡评分模型[J]. 华东理工大学学报（社会科学版）， 2008，23（2）： 49-52.

[12]Andrés J D， Lorca P， Juez F J， et al. Bankruptcy forecasting： a hybrid approach using fuzzy c.means clustering and multivariate adaptive regression splines （MARS）[J]. Expert Systems with Applications， 2011， 38（3）：1866-1875.

[13]弗兰克·奈特. 风险、不确定性与利润[M]. 安佳译. 上海： 商务印书馆， 2010， 225-252.

[14]Hu G H， Wang Y W. The application of data mining to customer credit analysis in medicament enterprise[C].New York， NY， USA ： IEEE， 2008： 78-82.

[15]Yuan B， Klir G J， Swan.Stone J F. Evolutionary fuzzy c.means clustering algorithm[C]. New York， NY， USA ：IEEE FUZZ， 1995：2221-2226.

[16]朱卫东， 吴鹏. 引入TOPSIS法的风险预警模型能提高模型的预警准确度吗？——来自我国制造业上市公司的经验证据[J]. 中国管理科学， 2015， 23（11）：96-104.

[17]Zhang Y， Wang W， Zhang X， et al. A cluster validity index for fuzzy clustering[J]. Information Sciences， 2008， 26（9）：1275-1291.

（责任编辑：钟 瑶）endprint