玻璃风琴的发声原理和制作方法

叶永鹏 张军朋

(华南师范大学物理与电信工程学院,广东 广州 510006)

图1 玻璃风琴

高脚红酒杯可以通过摩擦杯口发出音调稳定的声音,这种声音悠长且纯净,被不少艺术家称为“天堂的声音”.依靠一定的调音手段,多个合适的红酒杯可以产生音阶并组成乐器,这样的乐器即为玻璃风琴(Glass Harp).玻璃风琴的历史可以追溯到18世纪,著名科学家Benjamin Franklin制成了第一台可用于大型演奏的玻璃风琴并为其谱曲.著名作曲家Mozart也曾为玻璃风琴谱写过作品.直至今日,仍存在许多像Bruno Hoffman、Robert Tiso这样的玻璃风琴演奏家.通过网络,越来越多的人可以欣赏到的玻璃风琴优美的声音.[1]

玻璃风琴除了有丰富的艺术价值外,还有一定的教学价值.一方面,摩擦可以让玻璃风琴发出音调稳定的声音.这一现象可用受迫振动与共振的知识解释,了解其原理可以加深对受迫振动与共振的理解,因此玻璃风琴可以用于物理教学中.另一方面,制作玻璃风琴是一个探究过程,可以培养学生的动手能力与科学探究能力,因此可以将其作为一种课外探究活动.除此之外,玻璃风琴能有效激起学生的好奇心,让学生认识到物理与音乐之间有着密不可分的联系,因此其可以作为科学与艺术的桥梁,让学生对物理与音乐有更深刻的认识.因此,了解玻璃风琴的发声原理和制作方法将对教学具有帮助.本文将对此进行简述.

1 仪器原理

1.1 玻璃杯的振动分析

玻璃杯通过摩擦引起的振动属于受迫振动,但与典型的受迫振动不同,玻璃杯的振动并不是由周期性的外力引起的,而是由摩擦引起的.为什么摩擦能够引起玻璃杯的振动?摩擦学的研究表明,物体因摩擦而引起的振动源于两个表面之间的“粘滑现象”(stick-slip).这一现象大致可以理解为如下的过程,如图2为微观视角下,不平整杯口的一个凸起,其顶端与运动的手指接触.起初接触点与手指粘结在一起,与手指保持静止.随着手指的运动,接触点受到的切向弹性力不断增大,因此接触点不可能一直与手指保持静止,于是当弹性力大于粘着力时,接触点会滑移至平衡位置,成为扰动源,激起玻璃表面的弯曲波,带动整个玻璃杯的振动.[2]可以看到,“粘滑现象”在激励玻璃杯的过程中扮演了非常重要的角色.设想如果手指与杯口之间只有滑动而没有粘滞,那么无论如何都不能激起玻璃杯的振动.实验也发现,润湿的手指可以轻松地使玻璃杯发出声响,而干燥的手指却非常困难,这是因为浸润的液体能使手指与杯口有更强的粘滞.这一结论与上述分析一致.事实上,我们熟知的小提琴,其声音也是由琴弓与琴弦的摩擦产生,琴弦的振动也是源于“粘滑现象”.[3]而实验证明,涂有松香的琴弓或者是手指也确实可以使玻璃杯发出声音.

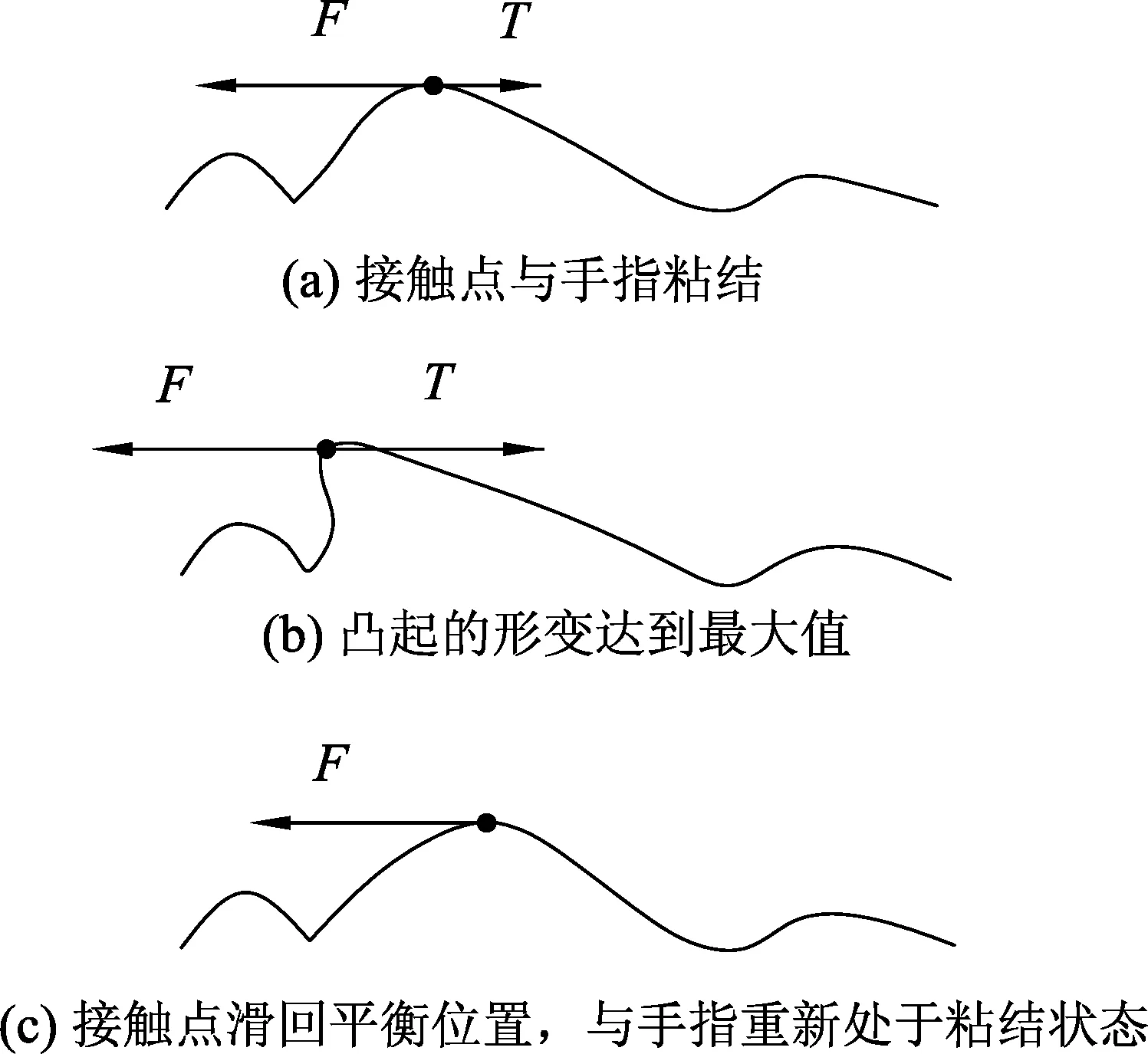
图2 粘滑现象

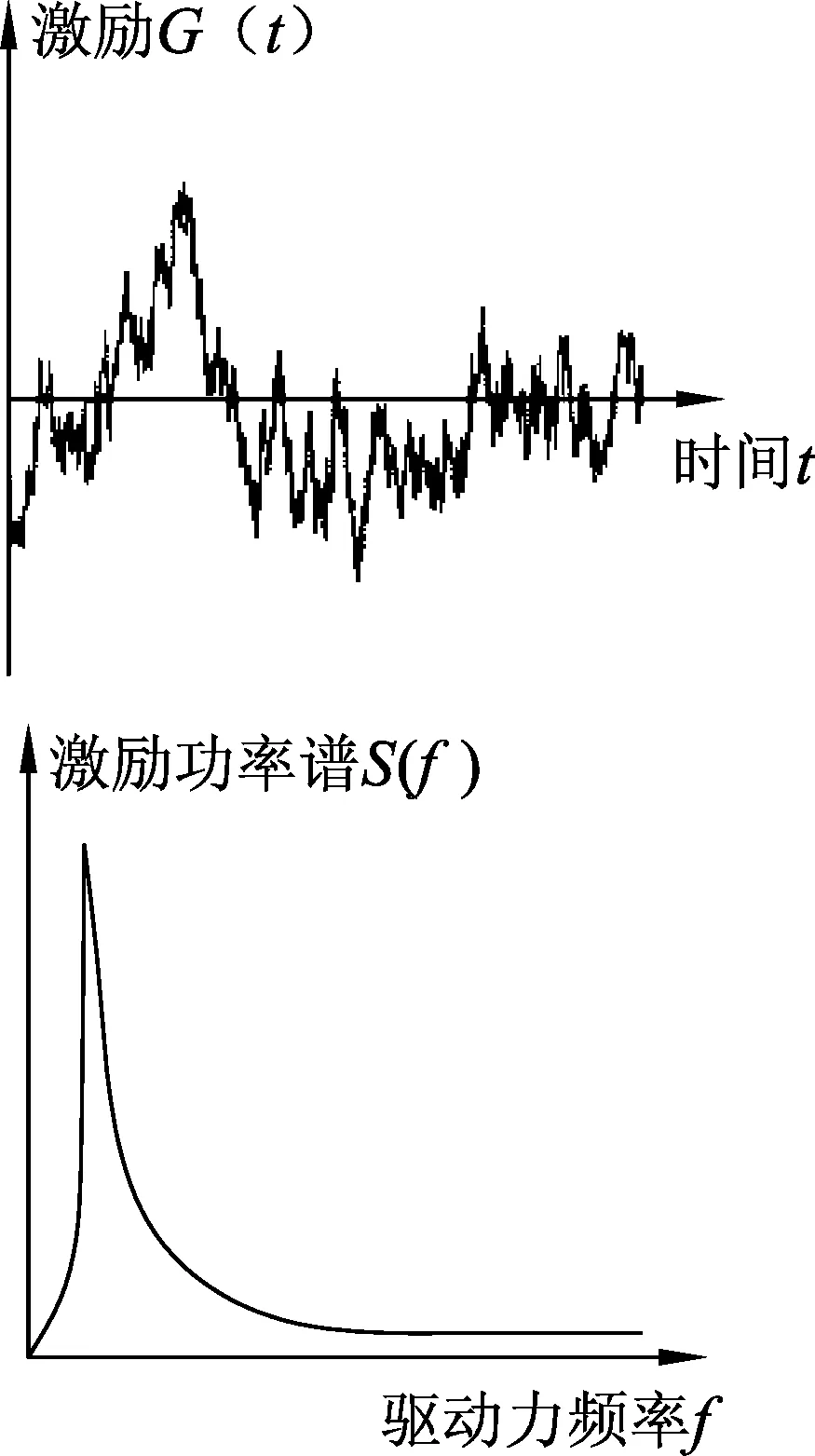
图3 随机激励的时域-频域分析

由于玻璃杯表面的不规则特性,手指对玻璃杯的激励并非是周期性的,而是随机的.因此从激励类型看,摩擦引起玻璃杯的受迫振动属于随机振动.在振动力学里,分析随机振动,可以采用傅立叶分析方法,把复杂的、随机的驱动力看成是无数个频率不同的驱动力叠加的结果.如图3为某个不规则表面的随机激励的时域图经快速傅立叶变换后(FFT)的频谱图.[4]也就是说,系统所受的驱动力频率覆盖了一个频率范围.假设这个范围涵盖了系统的固有频率,则根据受迫振动的频率规律可知,这无数个驱动力都将使系统做对应频率的受迫振动.然而,根据共振产生的条件,只有振动频率等于固有频率的受迫振动才具有大的振幅,而其他频率的振动则由于激励频率离固有频率太远,振幅太小,因而难以被感觉.

总之,我们认为手指作用在杯口的摩擦力可以等效为一系列频率不同的驱动力的叠加.这些驱动力使得玻璃杯做着有多个振动频率的复合受迫振动,又因为共振条件的存在,系统可以对这些受迫振动进行筛选,放大固有频率的振动而抑制其他频率的振动.这即是为什么摩擦玻璃杯时,人耳听到的音调是固定的,且声音的频率总是与玻璃杯固有频率相等.

1.2 玻璃杯的固有频率

玻璃杯属于弹性连续体,作为振动系统有着无穷多个固有频率.实际情况下由于高阶的振型振幅过小,可以分辨的固有频率非常有限,而研究发现,人耳直观感受到的音调主要取决于其一阶固有频率(基频),其他固有频率则决定了声音的音色.国外研究者A.P.French利用能量法推导了一阶固有频率的表达式

由表达式可知,决定固有频率的因素包括玻璃杯的密度ρg、杨氏模量Y、杯壁平均厚度a、杯腔的等效高度H以及等效半径R.由于玻璃杯的等效高度H与等效半径R难以确定,因此该表达式并不适用于玻璃杯固有频率的确定,但这一公式对我们预测玻璃杯的固有频率有一定的帮助,例如从表达式可知,在材质、厚度、以及等效半径相同的情况下,杯腔高度越高的玻璃杯固有频率越低.这些定性分析的结论也与实验相符.[5]

以上探讨的是仅以玻璃杯为振动系统的情况.若玻璃杯内盛有液体,则振动系统由玻璃杯与水共同组成.此时系统的固有频率将低于空杯状态下的固有频率,并且很容易观察到水量越多,产生声音的音调越低.文献[6]中对这种现象进行了研究,并通过实验测定了某玻璃杯的固有频率与水量的关系,其结果如图4所示.可以看出随着水量的增加,玻璃杯的固有频率下降得越来越快,而在接近满杯时频率下降与水量基本成线性关系.相比于空杯状态,满杯时的固有频率大幅下降.[6]然而实验发现,水量增加会使得玻璃杯振动的振幅变弱,因此,对于玻璃风琴而言,改变水量可调节的音调范围是有限的.一般而言,频率的改变量不能超过玻璃杯固有频率的25%(大约为二或三度的音程).

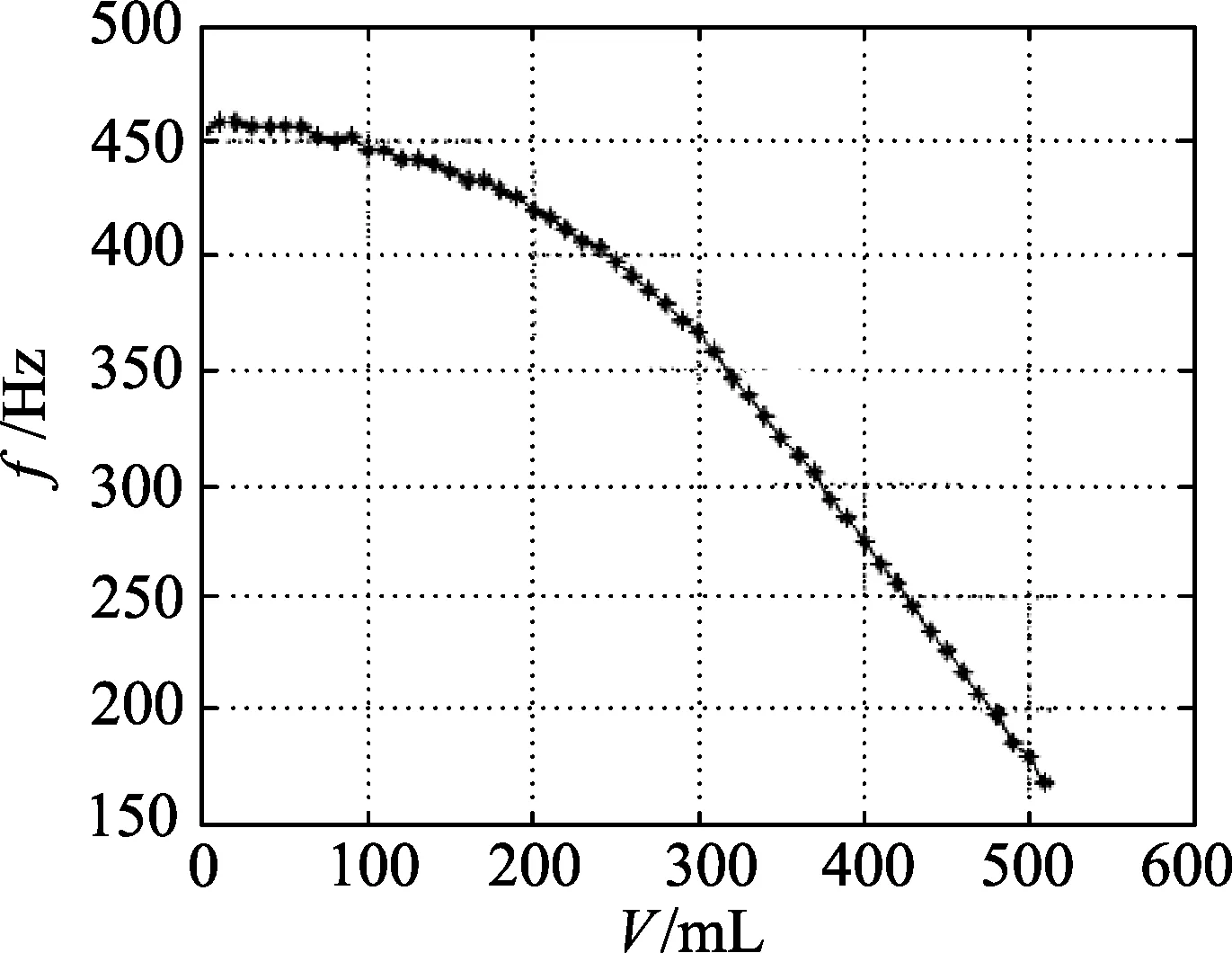
图4 玻璃杯固有频率f与水量V的关系

图5 调音软件测定玻璃杯固有频率

确定玻璃杯的固有频率可采用实验测定的方式,借助装有调音软件或频谱分析软件的智能手机可以很容易地完成测定.在测定时,可通过敲击引起玻璃杯的自由振动,调音软件(以安卓软件Best Tuner为例)能直接测得声音的频率(如图5),除此之外也可通过频谱分析软件的实时采样,得到玻璃杯声音的频谱图(如图6),其中图像的尖峰便对应着玻璃杯的固有频率,尖峰的高度对应着该频率振动的强度.可以看到,频谱图有多个高度不同的尖峰,表明玻璃杯有着不同的固有频率,且各个固有频率对应的振动强度也并不相同.

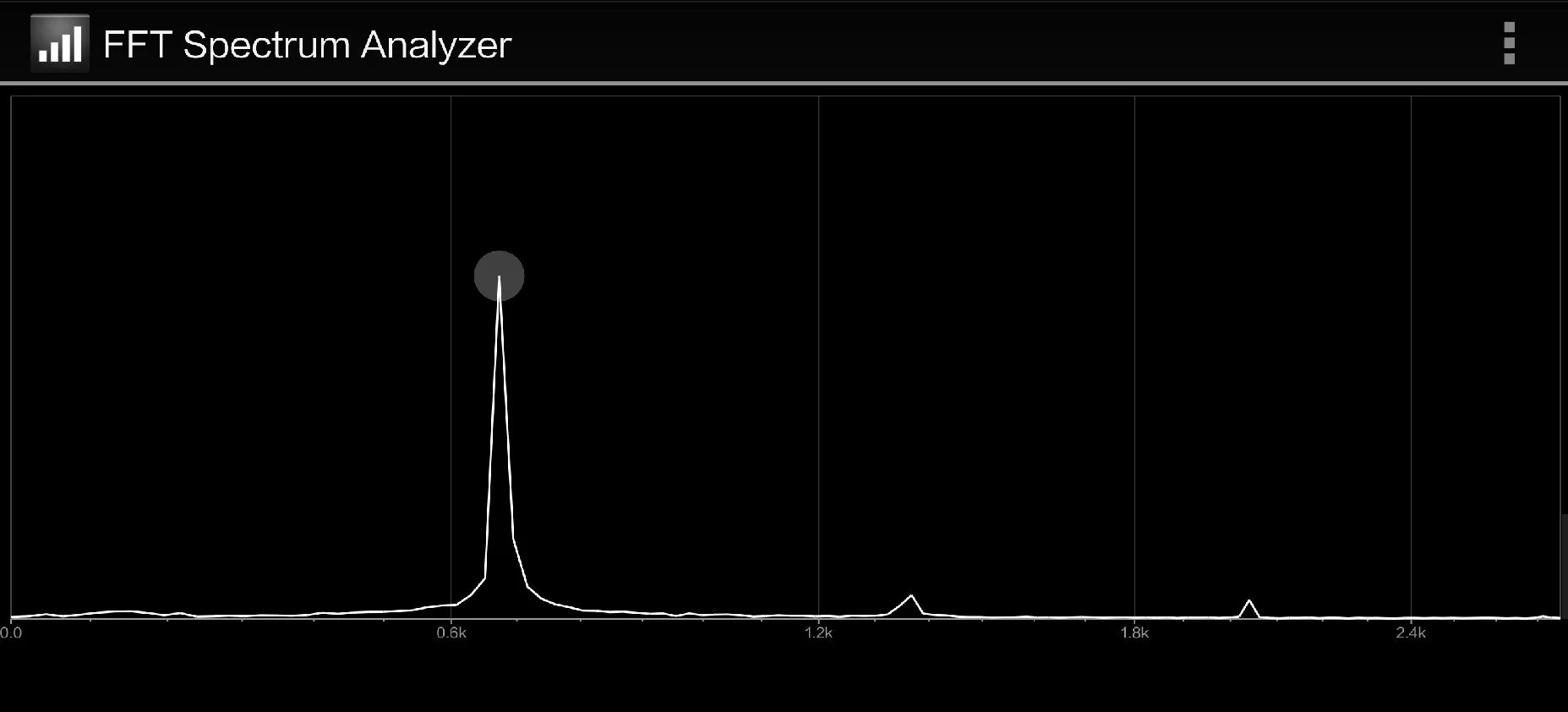
图6 玻璃杯声音的频谱分析

2 仪器制作

2.1 选择要表演的乐曲

在选择乐曲时,应注意以下问题.一是歌曲的音阶跨度不宜太大,这是因为固有频率太高或太低的玻璃杯比较难找.二是歌曲的音符数不宜过多,节奏也不宜过快,否则表演时双手会难以操作;除此之外,歌曲太简单也难以激起学生的兴趣.因此歌曲难度要适中.例如《我和你》、《欢乐颂》等经典音乐,下面将以《我和你》为例,介绍仪器制作的步骤.除此之外,也可选择制作完整音阶的玻璃风琴,这样可以演奏更多的乐曲.

2.2 确定频率关系

在确定所要演奏的歌曲后,为了选择合适的玻璃杯,可以先根据乐谱确定相对频率.这需要对音律知识有一定的了解.根据十二平均律,两个倍频音之间的频率差(即一个八度的音程)可以按比例平均分成12份,每等份称为半音程,每两等分称为全音程.由此我们得到了一个有13项的等比数列,数列的公比为21/12,即每个音的频率为前一个音的21/12(约为1.059)倍.我们所熟知的自然音阶(Do-Re-Me-Fa-Sol-La-Xi-Do)即是按“全-全-半-全-全-全-半”的音程排序的,各音符的音程关系以及频率关系可用图7总结.其中f是某个已知的参考频率.依照上述结论还可以推出相邻八度音对应的频率,例如1对应的频率是0.5f,而5是0.75f.

图7 十二平均律中唱名与频率的关系图

根据《我和你》的简谱,结合以上频率关系,可以确定包含的唱名以及对应的相对频率,如表1.

表1 《我和你》包含的唱名及频率

2.3 选择合适的玻璃杯

选择合适的玻璃杯是仪器制作的关键,一方面,玻璃杯的声音的音色和响度可能因材质和加工工艺的不同而大相径庭.在玻璃材质方面,常见的有普通玻璃和水晶玻璃,其中水晶玻璃比普通玻璃更硬,透光率更高,以此为材料的玻璃杯的声音会更为清脆.在处理工艺方面,制作通常有冷切口处理和卷口处理两种工艺,采用冷切口工艺的玻璃杯声音更明亮,音色也更纯净.因此,在挑选玻璃杯时我们应选择采用冷切口加工工艺的水晶玻璃杯.为了获得更多的固有频率,在挑选时,可以在大型家居市场或者是电商购买多种不同规格的玻璃杯.

图8 卷口工艺的玻璃杯

2.4 调音

使用调音软件测定各个玻璃杯的固有频率,根据前面确定的频率关系,挑选适合的玻璃杯,并推算出各个频率的精确值,如表2.其中音调偏高的玻璃杯,可通过加水来进行微调.此后每次演奏前,这些玻璃杯都需要根据确定的频率值重新加水调音.

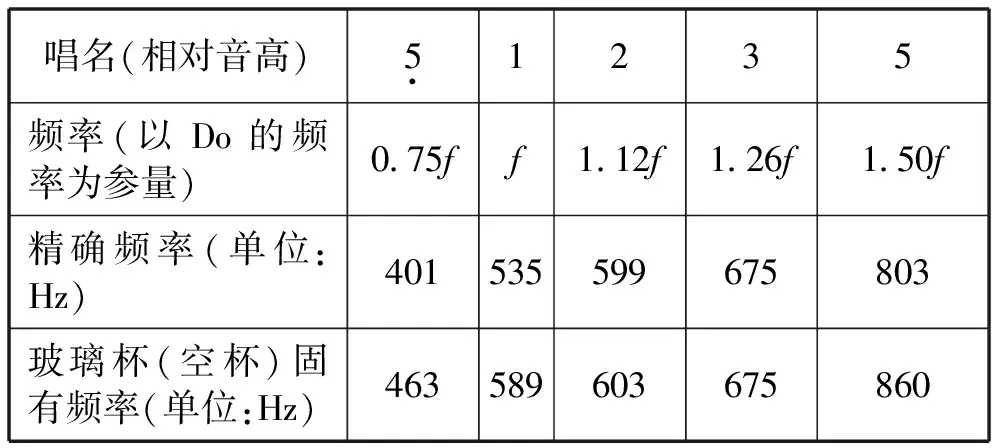
表2 《我和你》包含的唱名、频率、精确频率以及玻璃杯固有频率

2.5 玻璃杯的固定和仪器的组装

选取一块厚度超过3mm的木板或泡沫板,将定调的玻璃杯放置于木板上,按音阶顺序排成圆弧状(凹向演奏者),选取杯底圆周的4个对称点,用铅笔标记其在木板上的位置.取走玻璃杯,用电钻在标记点上对木板开孔,开孔完毕后即可用两条尼龙扎带将玻璃杯固定(图10).再在木板的底部加装垫高块,完整的玻璃风琴即组装完成.日后需要更换玻璃杯时,拆下扎带重新安装即可.

图10 用扎带将玻璃杯固定

3 结语

玻璃风琴的演奏可以有效地吸引学生的注意力,但其并非只是一个噱头.实际上,相比于教材介绍的驱动力周期变化的受迫振动,随机激励的受迫振动在日常生活中更加常见,例如气流引起的大桥的振动与汽车在路面上的颠簸.这些振动都与玻璃杯的振动类似,它们的驱动力频率都覆盖了一定的范围,在系统的选择下,系统做出特定频率的受迫振动.因此在教学中,可以以玻璃风琴为例子,分析此类随机激励的受迫振动,加深学生对共振现象的理解.除此之外,制作玻璃风琴也可以作为一个学生探究活动,发展学生的探究能力与动手能力.为达到演奏的效果,学生需要对音乐知识有一定的了解,这切合当前流行的“STEAM”的教育理念,让学生体会科学、技术、工程、艺术与数学之间的关系,从而使其综合能力得到全面发展.

1 T D Rossing. Acoustics of the glass harmonica[J]. The Journal of the Acoustical Society of America, 1994(95):1106-1111.

2 庄表中, 黄志强. 振动分析基础[M]. 北京:科学出版社, 1985：112-122.

3 胡元中. 提琴声中的摩擦原理[J]. 力学与实践,2008(05):110-111.

4 吕士宝. 车辆随机振动响应分析与计算[D].兰州交通大学,2013：11-18.

5 A P French. A study of wineglass acoustics[J]. American Journal of Physics, 1983(51):688-694.

6 宋徐林,王昆林. 利用DIS数字化信息系统对高脚玻璃杯振动声现象的研究[J]. 物理实验,2015(03):43-46.