小浪底水库异重流高效输沙理论与调控
张俊华,马怀宝,夏军强,李 涛,,王远见
(1.黄河水利委员会 黄河水利科学研究院,河南 郑州 450003;2.武汉大学 水资源与水电工程国家重点实验室,湖北 武汉 430072)
1 研究背景
小浪底水库是黄河下游防洪及供水安全、生态环境改善的保障。水库在调水调沙过程中往往产生异重流,实现水库异重流高效排沙,延长水库生命周期具有巨大的社会经济效益。围绕水库异重流,范家骅[1]、Wang[2]、Li[3]、Singh[4]、焦恩泽[5]、张俊华[6]等通过官厅、三门峡、小浪底等水库实测资料分析,或结合理论推导、水槽试验、物理模型试验等开展了广泛研究。黄委通过黄河调水调沙将研究成果应用于实践[7]。然而,在水库实际调度过程中,仍面临有待深入研究的问题。其一,由于水沙过程极不均匀、地形时空变化剧烈,加之库水位变化频繁,使得异重流潜入位置变化多端,运动过程极不稳定,目前,尚缺乏适用于描述动边界与动约束条件下异重流产生与运动方程。其二,支流淤积源于干流倒灌,口门往往形成拦门沙,其高程以下支流库容成为难以参与水库正常调度的“无效库容”。干流异重流对支流的倒灌削弱了异重流的能量,倒回灌过程的相关因素及其之间的影响机制尚不明晰,且尚无系统完整的原型观察资料。其三,水库异重流排沙过后,往往沿库区分布一层由细颗粒泥沙悬浮其中的浑水层,或滞留坝区形成浑水水库,本文定义两者为“滞留层”。滞留层中黏性悬沙沉降并沿垂向“浓缩”,到一定浓度后转化为浮泥[8-9],进而转化为沉积物淤损库容。由于细颗粒泥沙在黄河下游基本上可作为冲泻质,故沉降在水库中并不能起到拦沙减淤的作用而被视为“无效拦沙”。显然,适时开启排沙洞,或借助于后续洪水异重流的能量,启动滞留层并随之排出库外,可达到高效排沙的目的。韩其为院士认为[10],异重流畅流与浑水水库结合后的排沙效率最高。但由于观测资料匮乏,且相关试验研究尚不能满足工程应用的需求。
因此,深入开展复杂边界异重流潜入与运动规律、干支流倒灌机制、滞留层中具有黏着力的细颗粒泥沙演变及其与后续异重流的相互作用等方面的研究,是实现水库高效输沙的基础与关键技术。
2 复杂边界异重流潜入条件
在分析异重流含沙量与流速垂线不均匀分布对异重流运动影响的基础上,推导异重流运动控制方程,提出新的异重流潜入条件判别式,并用多组模型试验及野外实测资料对该判别条件进行验证。
2.1 压力修正系数若假定异重流平均浑水容重γm沿水深不变,则异重流厚度内的总压力P可表示为:

式中:γc为清水容重;hc为清水厚度;z为垂向坐标;hm为浑水厚度。
实际上,异重流浑水容重沿垂向分布并非均匀分布,特别是较高含沙量异重流不均匀性更为显著。令ηg为异重流某一点浑水容重,异重流厚度内的总压力为:
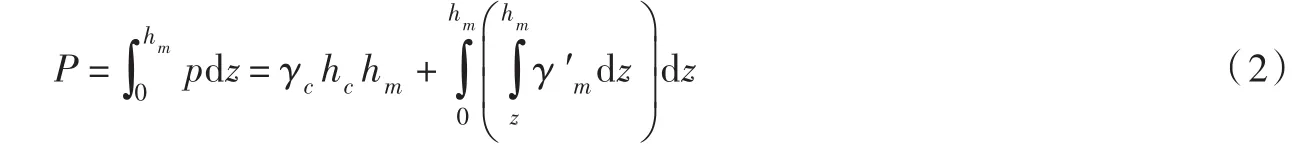
对比式(1)与式(2),可引入压力修正系数km,其定义式为:

由于垂线上任一点浑水容重γ′m与含沙量s的关系可用式表示,含沙量沿水深分布可采用张红武等提出的悬移质含沙量沿垂线分布公式[11]:

式中:sa为近底(z=a)含沙量;ξ=a/hm。

由式(5)可知压力修正系数km主要与近底含沙量大小、悬浮指标等因素密切相关。
选择黄河小浪底水库实测资料计算得到km值一般小于1。如图1所示的两次含沙量垂线分布观测资料,计算km值分别为0.964与0.774,表明引入压力修正系数km是必要的。
2.2 动量修正系数由于异重流垂向流速沿垂线分布的不均匀性,引入了动量修正系数αm:

式中:u′为异重流垂线上点流速;um为异重流垂线平均流速。
若认为流速沿垂线分布:①服从对数规律,则αm=1+g/C2κ2,C为谢才系数,κ为von Karman常数,一般取0.4;②符合1/7幂函数规律,则αm=1.016;③服从表层及底层流速均为0近似的二次抛物线规律,则计算的动量修正系数αm一般大于1.1。
图2给出小浪底水库实测异重流流速沿垂线分布图。由式(6)可计算得到两条垂线上的动量修正系数αm分别为1.196及1.423。因此流速不均匀分布引起的动量修正系数对异重流潜入点判别条件的影响同样不能忽略。

图1 异重流含沙量垂线分布

图2 潜入点处流速沿垂线分布
2.3 异重流动量方程引入浑水容重及流速沿水深分布的不均匀修正系数后,以此推导非恒定异重流运动的动量方程。异重流受力情况见图3,分别考虑压力P1、P2、P3,重力G,阻力项T(包括床面、交界面),惯性力项I,表层清水以uc的速度往上游流动而对异重流产生的附加力Tc,故力的平衡方程式应为:

将有关各力的表达式代入式(7),化简可得:


图3 非恒定异重流运动过程的受力分析
式中:hc、hm分别为清、浑水层的厚度;fm为异重流综合阻力系数;τc为附加阻力;Zb为河底高程。
2.4 异重流潜入点判别公式异重流运动的力学特性之一是有效重力大大减小。和一般明渠水流一样,维持异重流运动的动力仍是重力。

式中γc、γm分别为清、浑水容重。可见由于清水的浮力作用,浑水的重力加速度减小到ηg倍,又因ηg的量级一般为10-3~10-1,故异重流的重力作用大为减弱。
引入含沙量浓度S(kg/m3),则浑水密度ρm可表示为ρm=ρc+( )1-ρc/ρsS 。当含沙量S 在 1~400 kg/m3之间变化时,利用浑水密度ρm、清水密度ρc、泥沙干密度ρs、体积比含沙量SV可得:

对于高含沙异重流,考虑体积比含沙量对异重流潜入点形成的影响,即:

式中:Frp为潜入点处的Froude数;为体积比含沙量SV的某一函数。
点绘范家骅等的相关水槽试验与黄河水利科学研究院小浪底水库物理模型试验资料,潜入点Froude数Frp与体积比含沙量SV之间的关系可用下式表示:

将式(12)两边同除以式(10),潜入点处的密度Froude数Fr′p的平方与体积比含沙量SV关系可用下式表示:

将qp=uphp代入式(12),则可得潜入点水深与单宽流量及体积比含沙量之间的表达式,即:

采用式(14)计算潜入点位置特别是对于高含沙水流,结果更加接近实测值[12]。表明新的异重流潜入公式给出了含沙量与密度Froude数的显性关系式,可较为准确地判别一般含沙量与高含沙异重流的潜入位置,更适应水库调度过程中,异重流潜入点位移幅度大、变化频繁及局部库段输沙流态更迭变换的情景。
3 水库支流异重流倒灌淤积计算
采用理论推导与水槽试验等方法得到异重流支流倒灌流速、流量表达式,并采用多元优化方式,建立支流拦门沙抬升值和淤积量与水沙过程、地形变化、局部输沙流态的多元响应关系,并得到实测资料的验证。
3.1 异重流倒灌流速用脚标0代表支流倒灌前浑水有关参数,脚标a代表支流内部浑水层,脚标b代表支流内部清水层有关参数。
令干流行近流速为U0,可得动量方程为:

式中:γm、γc为浑水和清水的容重;α为流速分布不均匀系数;h为水深;U0为行近流速;Ua为支流内异重流头部流速。P0、Pb分别为异重流进入支流前、后清水压力。Pa为异重流进入支流后浑水压力。

忽略行近流速,令U0=0,得到韩其为推导的异重流倒灌流速公式:

式(16)可变形为:

可以得到:

式中Frrin、Frrtri分别为倒灌支流的异重流、支流内异重流的Froude数,因为上式等式左边且所以,
进而得到:

因此,倒灌支流的异重流为缓流。
由于

所以ha≤h0,即倒灌支流的异重流厚度随着沿程衰减,其值不大于口门水深。
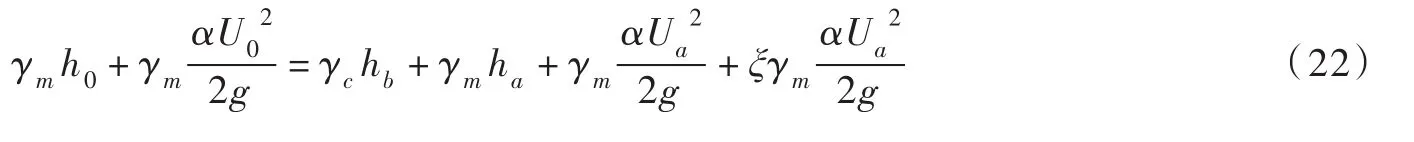
整理可得:

当式(23)中U0、ha为0时,即为韩其为推导的倒灌流速公式形式[13]。
3.2 异重流倒灌流量令h0为干支流交汇处的干流异重流厚度,h1为潜入后的异重流厚度,支流底坡为J,潜入段长度为L0,ξ为阻力损失系数,见图4。

图4 异重流倒灌示意图
忽略来流行近流速,可写出两断面间的伯努利方程:

式中:γc、γm分别为清、浑水容重;U1为潜入后异重流流速。令K2=h2/h0,ηg=(γm-γc)/γm,将上式变形为:

令潜入段的交界面方程为zt=f(x),坐标原点位于B点,对于浑水体ABCD列出动量方程:

式中:等号右边第二个积分项为CD面上的压力;第三个积分项为底坡BC上的压力。引入K2和ηg,则上式变为:

关于潜入段的交界面曲线方程,Benjamin曾对于无能量损失的理想情况给出了近似解[14],但解的形式为非常复杂的参数方程。这里将交界面近似为连接AD的直线来计算式(26)中的积分,然后联立式(26)、式(27)得到K2的表达式:

倒灌流量Q=U1h1,将式(25)、式(28)以及h1=(1-K2)h0-JL代入,可以得到异重流倒灌流量公式如下:

由式(29)可知,倒灌流量与口门异重流厚度的3/2次方以及有效重力加速的1/2次方成正比。
采用黄委水文局观测29测次的小浪底水库支流沇西河、西阳河、畛水河及大峪河的异重流倒灌数据[15],对式(29)进行了验证[16],公式计算的均方根误差为 1.555 m2/s,R2=0.89。
3.3 支流拦门沙演变关键因素及作用机制支流拦门沙形成与发展影响因素众多。采用无量纲化的物理指标作为自变量和因变量进行多元统计分析。由于水沙过程、局部地形条件和局部输沙流态之间存在无法解耦的相互关系,因此,本分析中各影响指标将以指数乘积的形式出现,即多元回归公式的最终形式为:

由于研究对象是拦门沙,因此,将每年支流拦门沙高程抬升值Δh与每年支流的总淤积量ΔV分别作为因变量,将其无量纲化得:

式中D50为支流入汇干流断面处每年汛前床沙质的中值粒径。
选择黄委水文局观测的小浪底库区畛水、石井河、东洋河、西阳河、沇西河等主要支流2001—2014年调水调沙期逐日坝前水位、逐日入、出库流量、汛前、汛后地形断面、逐日含沙量资料[15],分析支流拦门沙与来水来沙过程、干流淤积形态、干流输沙流态等因子之间的响应关系,采用多元优化的方式,建立小浪底库区支流拦门沙高程抬升值和支流淤积量与水沙过程、地形变化、局部输沙流态等因素的多元响应关系:

式中:Q*为汛期出库平均流量,m3/s;g为重力加速度;Bh为支流沟口宽度,km;Bm为支流最大宽度,km;L0为支流口门距坝里程,km;L为三角洲顶点距坝里程,km。
4 异重流高效排沙试验研究
基于理论推导与水槽试验,对滞留层演变特性及其与接踵而来的后续异重流之间的响应机制开展系统研究,为减少水库“无效拦沙”的优化调度提供支撑。
4.1 场次异重流之间的运动形式基于水槽比降、进口流量与含沙量等条件组成了20组次异重流叠加试验,各场次异重流时间间隔约2~24h,观测异重流与前期滞留层之间的作用机制。由于滞留层中悬浮的泥沙在自重作用下沉降压缩,场次异重流之间的间隔时间不同,滞留层泥沙浓度存在较大的差异。

图5 侵入型异重流头部

图6 界面型异重流头部

图7 多场次异重流叠加试验
4.2 异重流流态与流速从雷诺数计算分析表明异重流处于紊流区,其中侵入型异重流紊动强度受到前期滞留层抑制作用,紊动强度小,而界面型异重流紊动强度相对较大。从Froude数计算结果看,同一场次洪水异重流在运动过程中,可出现急流到缓流的变化。
界面型异重流平均流速大于侵入型平均流速,这说明异重流头部以侵入型运行时与前期滞留层掺混,遇到的阻力较界面型大。
4.3 异重流滞留层对后续洪水的响应由于异重流携带泥沙颗粒较细,滞留层一般以浑液面形式整体下沉,沉速极为缓慢。如小浪底水库2010年10月19日至2011年7月1日期间,坝前浑水水库经历干扰网体沉降和整体密实下沉状态,浑液面仅下降1 m。
后续异重流是在清水与前期滞留层这两层不同密度的介质中传播。当前期滞留层的屈服切应力大于异重流有效切应力时,前期滞留层表现为“固态”。反之,前期滞留层表现为“液态”,两者之间产生了应变速率,滞留层发生运动。两者状态可用流动判数I=τ/τB加以判断。
其中,τ为有效切应力:

式中:γm、γc分别为异重流形成的浑水、清水容重;hm为异重流水深;Jm为河底比降。
τB为宾汉极限剪切应力,抽取小浪底水库坝区浑水制作不同浓度悬液,得出τB随含沙量、中值粒径变化:
式中:Sv为体积比含沙量;D50为悬沙中值粒径。
引入前期滞留层的流动判数σ,代表两种浑水体有效切应力与宾汉极限剪切应力的对比。由式(35)、式(36)可得:
由于前期滞留层物理特征沿流程分布存在差异,加之后续异重流在运行过程中,含沙量沿程不断调整,因此流动判数σ沿程会发生变化。
在水库调度过程中,可根据滞留层演变特征,预测其容重等基本参量变化过程;根据后续洪水水沙过程,预测异重流潜入与输移过程。由此可算得判别指标M 与σ值,把M>0记为1,M=0记为0,M<0记为-1;把σ>1记为1,σ=1记为0,σ<1记为-1,可列出表1所示的判别矩阵。当满足M=0,σ>1时,可达到高效排沙的目的。

表1 滞留层运动状态判别矩阵
5 水库高效输沙调度原则
水库高效输沙调度目标是尽可能减少“无效拦沙”。在实际水库调度中,运用本次提出的计算方法,跟踪预测滞留层含沙量分布、厚度及其随时间变化,以及可动性等特征指标。结合黄河中上游来水来沙过程,适时开展水库(群)优化调度,使得库区形成的异重流能量大于前期滞留层运动的动能,不仅满足本次异重流尽量多的排沙出库,而且又使前期滞留层尽可能较多的随之排出,满足水库高效输沙的目标。
(1)适时开启水库泄水孔洞。在无后续洪水入库的情况下,适时开启排沙底孔,将坝前仍具有可动性的滞留层排泄出库,提高水库排沙效率。
(2)利用黄河中游洪水。依据洪水量级及持续时间,结合水库边界条件及滞留层特征,优化调整水库调度方式,并实时跟踪,动态调整,以同时提高异重流与前期滞留层排沙效率。
(3)利用黄河中游水库群塑造洪水。近期可利用黄河中游万家寨、三门峡、小浪底水库联合调控,塑造异重流,以减少滞留层的淤积。从远期看,黄河中游古贤水库投入运用后,大幅度增加了水库调节幅度,可为水库高效输沙提供更为有利的条件。
6 结论
本研究以黄河小浪底水库为背景,围绕库区复杂流态水沙输移规律等前沿科学问题开展基础研究。提出了可精确描述异重流产生、干支流倒回灌等复杂边界条件下水沙运动控制方程;开展异重流滞留层演变及其与后续异重流响应等全过程的研究与观测,以上述研究为基础提出水库高效输沙调度原则。
(1)在异重流动量方程中引入压力修正系数km、动量修正系数αm,推导了非恒定异重流运动的动量方程,给出了密度Froude数与体积比含沙量的显性函数关系,克服了以往潜入点判别条件中忽视密度Froude数与重力修正系数同时具有含沙量隐函数关系而存在偏差的缺陷。提出了同时适应一般含沙水流与高含沙水流的异重流潜入判别条件。更加适应小浪底水库动边界与动约束复杂状态下,异重流潜入位置瞬息万变,运动过程极不稳定的运动状态。
(2)水库干支流倒回灌与水沙过程、输沙流态、干支流交汇处局部地形、水库调度过程等因素的影响机制,并通过水库调度减缓支流拦门沙抬升速率既是学科难点也是工程问题的重点。本研究基于理论推导并通过水槽试验,揭示了支流拦门沙成因及其作用机制,提出水库干流异重流倒回灌支流淤积计算方法;采用多元优化的方式,建立小浪底库区汛期支流拦门沙高程抬升值、支流淤积量与水沙过程、地形变化、局部输沙流态的多元响应关系。
(3)系统开展了理论研究、多场次异重流叠加试验及原型跟踪观测。深入探讨了滞留层的演变过程与接踵而来的后续异重流水动力机制及其之间的响应过程。定义了侵入型与界面型两种不同运动状态的异重流。运用本次提出的计算方法,跟踪预测滞留层演变过程,以流动判别数等为指标,结合中上游洪水过程预测,提出满足水库高效输沙的调度方案。
研究成果为水库优化调度实现高效输沙、减少“无效拦沙”、降低支流“无效库容”等方面奠定了基础。
[1]范家骅.关于水库浑水潜入点判别数的确定方法[J].泥沙研究,2008(1):74-81.
[2]WANG Guangqian,FANG Hongwei.Basic equations for density current[J].Chinese Science Bulletin,1996,41(16):1402-1408.
[3]LI Yuanya,ZHANG Junhua,MA Huaibao.Analytical Froude number solution for reservoir density inflows[J].Journal of Hydraulic Research,2011,49(5):693-696.
[4]SINGH B,SHAH C R.Plunging phenomenon of density currents in reservoirs[J].La Houille Blanche,2010,26(1):59-64.
[5]焦恩泽.黄河水库泥沙[M].郑州:黄河水利出版社.2004.
[6]张俊华,陈书奎,李书霞,等.小浪底水库拦沙初期水库泥沙研究[M].郑州:黄河水利出版社,2007.
[7]水利部黄河水利委员会.黄河调水调沙理论与实践[M].郑州:黄河水利出版社.2013.
[8]曹祖德.波浪作用下浮泥运动特性的研究[J].水道港口,1987(2):10-16.
[9]洪柔嘉,应永良.水流作用下的浮泥起动流速试验研究[J].水利学报,1988(8):51-57.
[10]韩其为,李淑霞.小浪底水库的拦粗排细及异重流排沙[J].人民黄河,2009(5):1-5,12.
[11]张红武.黄河下游洪水模型相似律的研究[D].北京:清华大学,1995.
[12]XIA J Q,LI T,WANG Z H,et al.Improved criterion for plunge of reservoir turbidity currents[J].Proceedings of the Institution of Civil Engineers-Water Management,2017,170(3):139-149.
[13]BENJAMIN T B.Gravity currents and related phenomena[J].Journal of Fluid Mechanics,1968,31(2):209-248.
[14]李涛,夏军强.多沙河流水库异重流潜入机理及支流倒灌机理研究[D].武汉:武汉大学,2017.
[15]黄委水文局.黄河小浪底水库水文泥沙及淤积测验资料汇编[R].2016.
[16]王增辉,夏军强,李涛,等.考虑底坡的异重流倒灌流量公式[J].泥沙研究,2017(1):1-5.

