泵站内部流动分析方法研究进展
王福军 ,唐学林 ,陈 鑫 ,肖若富 ,姚志峰 ,杨 魏
(1.中国农业大学 水利与土木工程学院,北京 100083;2.北京市供水管网系统安全与节能工程技术研究中心,北京 100083)
1 研究背景
泵站是跨流域与区域调水、农业灌溉与排涝、城市供水与排水等领域的重要基础设施。我国是世界上泵站数量最多、规模最大、类型最丰富的国家。南水北调东线工程13个梯级的34座泵站是世界上规模最大的梯级泵站群;南水北调中线工程惠南庄泵站装机功率6万kW,是世界上功率最大的双吸离心泵泵站;正在建设的黑龙江青龙山灌区渠首泵站装机流量381 m3/s,是世界上流量最大的混流泵泵站;正在建设的云南滇中引水工程石鼔泵站最大净扬程218.8 m,安装12台单机功率4.1万kW的离心泵,泵站装机功率49.2万kW,是装机功率仅次于美国埃德蒙斯顿泵站的世界第二大泵站。到目前为止,全国共有各类泵站31万座,装机功率1.6亿kW,年耗电近5400亿kW·h,约占全国总用电量的10%。其中,约一半的泵站直接为水利行业服务[1]。
泵站是由流体流动支配、固体结构控制的高耗能流固耦合系统,其水力性能直接影响调水、供水、排水系统的运行安全性、稳定性和工程效益[2]。由于泵站结构、水泵型式和运行环境的复杂性,由前池、进水池、进水流道等组成的泵站进水系统常存在自由表面旋涡和次表面旋涡,对水泵运行稳定性、效率和空化性能产生直接影响[3-4];在水泵内部,水泵自身的强旋转、大曲率、高剪切流动特点及其与进出水流道的耦合作用,导致泵站经常存在较大压力脉动和振动[5];在泵站出水系统中,特别是长距离输水系统的压力管道内部,经常存在因工况快速变化而造成的水力瞬变问题,甚至出现抬机和爆管事故[6-7]。因此,泵站装置高效稳定运行涉及到各过流部件水动力特性,采用流动分析方法对泵站设计进行评估,对现有泵站存在问题进行研判,对保证泵站安全、高效和稳定运行具有重要意义。
随着计算流体动力学(Computational Fluid Dynamics,CFD)[8-10]理论与技术的发展,泵站流动分析方法在进入21世纪后发生了很大变化。本文针对这些重要变化,对泵站流动分析方法及其应用情况进行分析和综述,为今后拓展泵站水力学研究,提高泵站设计与运行质量提供技术支持。
2 泵站内部流动分析方法
在1990年代中期以前,泵站流动分析总体上以一维水力学方法为主,主要通过经验公式分别针对泵站装置各部件水力损失、空化状态和压力分布等进行计算[2]。进入21世纪后,随着计算机的快速发展和CFD技术的不断完善,三维黏性流动分析方法逐渐成为泵站流动分析的主要方法[11]。该方法以泵站内部流动的连续方程和动量方程为基本控制方程,采用有限体积法对计算域进行空间离散,然后在离散的单元上求解代数方程组,从而得到各计算节点的速度和压力,进一步得到旋涡、流线和能量损失、压力脉动等分布情况,从而可准确预测泵站装置效率、空化性能和运行稳定性等指标。通过对流场细节的判断可进一步改进泵站设计,或找出已有泵站存在的问题[12]。这种方法涉及湍流模型、几何模型、网格模型、数值离散模型和解算模型等多个方面。
2.1 湍流模型泵站流动的雷诺数在绝大多数情况下大于104,属于湍流范畴,受连续方程和动量方程的支配。湍流所具有的瞬态性和非线性使得解析方法无法精确描述其三维空间及时间域上全部细节,况且湍流细节对于实际泵站工程来说也没有太大意义。这就需要对湍流计算进行简化,从而出现了不同湍流模型。目前泵站流动分析所用的湍流模型主要包括雷诺平均模型和尺度解析模型两大类[13]。
2.1.1 雷诺平均模型 雷诺平均模型(Reynolds-Averaged Navier-Stokes model,RANS)[14]在时间域上对流场物理量进行雷诺平均化处理,生成一组雷诺平均化控制方程,方程中包含雷诺应力项。根据对雷诺应力项的建模方式不同,出现了两类雷诺平均模型:涡黏模型和雷诺应力模型。
(1)涡黏模型主要包括Spalart-Allmaras模型、k-ε模型和k-ω模型。Spalart-Allmaras模型[15]只由一个方程组成,计算简单快速,在泵站流动比较平顺的条件下能得到工程上可接受的解。k-ε模型和k-ω模型均由两个方程来构成,计算精度较高,是目前泵站领域应用最为广泛的两组模型。
k-ε模型[14]引入关于湍动能k和湍动耗散率ε的输运方程来表征湍动黏度,现有各类k-ε模型均是在Launder和Spalding于1972年提出的标准k-ε模型[16]基础上改进而来。其中,RNGk- ε模型[17]使用了重正化群统计技术,通过修正湍动黏度考虑了平均流动中旋转及旋流情况,同时在ε方程中增加了反映主流时均应变率的一项,使得RNGk-ε模型可以更好地处理带旋流、高应变率流动及流线弯曲程度较大的流动,在包含水泵叶轮的泵站流动分析中展现出了明显优于标准k-ε模型的解析能力。Realizablek-ε模型[18]在湍动黏度中引入了与旋转和曲率有关的内容,并根据均方涡量脉动动态方程修正耗散率方程,从而可以用来模拟旋转均匀剪切流及带有分离的流动,在泵站进水池中可以更好地模拟表面旋涡和附壁涡[19]。
k-ω模型[20]用比耗散率ω的方程代替了k-ε模型中耗散率ε的方程,避免了构造复杂的非线性壁面衰减函数,降低了对近壁区网格y+的要求,不存在k-ε模型所具有的过高估计湍流输运作用的问题,可较好预测带有逆压梯度的流动分离问题。常用k-ω模型主要有3种:Wilcoxk-ω模型、Base⁃linek-ω模型和SSTk-ω模型。Wilcoxk-ω模型[21]也称标准k-ω模型,在预测自由剪切流时取得较好效果,比k-ε模型的预测精度有提高。然而,Wilcoxk-ω模型对自由来流ω值非常敏感,为此,Menter[22]开发了Baselinek- ω模型和SSTk- ω模型。Baselinek-ω模型[22]将Wilcoxk-ω模型与k-ε模型结合在一起,通过混合函数在近壁区使用Wilcoxk-ω模型,在近壁区之外及自由剪切流动中使用标准k-ε模型,从而既保留了Wilcoxk-ω模型在近壁区、k-ε模型在自由剪切层中各自的优势,又克服了Wilcoxk-ω模型对自由来流ω值的敏感性。Baselinek-ω模型的缺点是不能准确预测来自于光滑表面的流动分离起点位置及分离区大小,而SSTk-ω模型[22]则没有这一缺点,可有效预测逆压梯度条件下流体分离开始点和分离区大小[23]。越来越多的学者认为,SSTk-ω模型是泵站内部流动分析领域应该优先选用的两方程模型[24]。
(2)雷诺应力模型[9]针对雷诺应力张量的分量直接构造附加输运方程,更加细致地考虑了流线曲率、旋流、旋转及应变率的快速变化,摒弃了涡黏模型中的各向同性假定,因此,在求解复杂流动时可以给出更高的计算精度,但因其计算量大,在泵站工程中很少使用。
2.1.2 尺度解析模型 在将雷诺平均模型用于泵站流动模拟时,常存在两个问题:一是不适合于流场存在较大流动分离区的计算,如进水池存在大尺度旋涡的流动分析;二是不适合瞬态性较强的流动计算,如流场压力脉动分析。尺度解析模型(Scale-Resolving Simulation,SRS)[25]使流场中至少有一部分湍流被直接求解,需要较细密的计算网格和较小的时间步长,从而计算效率不如RANS,但在求解分离流动和瞬态性较强的流动时具有优势。近几年的发展使SRS本身不断完善,计算效率在不断提高。用于泵站流动分析的SRS主要包括大涡模型、尺度自适应模型、分离涡模型和嵌入式大涡模型。
(1)大涡模型(Large Eddy Simulation,LES)[26]通过滤波操作将小于滤波器宽度或计算网格尺度的小尺度涡过滤出去,只对各向异性的大尺度湍流运动进行求解,将接近各向同性的小尺度涡对大尺度运动的影响通过模型来表征。LES的核心是亚格子尺度应力(Sub-Grid-scale Stress,SGS)模型,它体现了小尺度涡对大尺度运动的影响。Smagorinsky模型[27]是最基本的SGS模型,几乎所有其他模型均是在Smagorinsky模型基础上发展起来的。动态Smagorinsky模型[28]消除了Smagorinsky模型需要选取经验常数的弊端,是目前使用最广泛的SGS模型。壁面自适应局部涡黏模型[29]具有动态Smagorinsky模型的优点,但不需要二次滤波,计算简单,在层流到湍流的转捩流计算方面具有优势。代数壁面建模LES模型[30]避免了必须在近壁区垂直和平行于壁面方向划分细密网格的特殊要求,提高了适用性[20]。动能传输模型[31]采用二次方关系代替传统的一次方关系来表达SGS应力,提高了理论完备性,但该模型有待于实践的检验。最近几年,一批组合式SGS模型开始得到应用,例如,杨正军等[32]将动态混合模型和动态非线性模型组合到一起,提出了动态混合非线性SGS模型。模型无需SGS应力主轴与可解应变率主轴对齐,考虑了各向异性效应和旋转效应,计算效率和精度都有所提高,周佩剑等[33]利用此模型成功模拟了瞬态性极强的水泵旋转失速涡团。此外,Li等[34]将基于涡量梯度张量的螺旋度加入亚格子应力,构建了带有螺旋度修正的SGS模型,为泵站吸水喇叭口的螺旋流动提供了一种新的计算模式。
(2)尺度自适应模型(Scale-Adaptive Simulation,SAS)由 Menter等[35-36]提出。虽然LES在工程上得到了比较广泛的应用,但它存在计算成本高、对含有涡脱落的大分离复杂流动模拟精度差的弱点,因此出现了多种针对LES的改进模型。SAS在流场的定常和非定常区域分别采用定常RANS和非定常LES求解,在模拟大分离流动时表现良好。
(3)分离涡模型(Detached Eddy Simulation,DES)由 Strelets等[37]提出。将 RANS用于求解近壁区的贴合流动和弱分离流动,将LES用于求解湍流核心区流动。DES也常被称为混合LES/RANS模型[10],兼顾了RANS和LES的优势,是一种具有应用前景的复合式模型,美国Iowa大学Constanti⁃nescu团队[38-39]通过在泵站进水池旋涡分析中采用不同湍流模型对比证实了这一结论。
(4)嵌入式大涡模型(Embedded Large Eddy Simulation,ELES)[20]是许多商用CFD软件近几年新增加的模型。允许在网格划分时就人为将流场划分为若干个区域,在每个区域分别指定RANS或LES求解模式,而在区域的分界面上指定湍流转换机制。ELES在理论上较完备,但尚未在泵站中得到实际应用。
2.2 几何模型用于泵站流动模拟的几何模型包括计算域和边界条件两部分。计算域是实施流动分析的空间区域,通常是在水体域所占据的物理空间基础上,根据计算目的所抽象概括出的三维或二维几何空间。计算域通常只包含水体域,如果进行进水池自由水面波动情况分析,还需包含水面以上的部分空气域。计算域通常有两种类型:整体式和分散式[40]。
(1)整体式计算域是指将泵站前池、进水池、进水流道、泵段、出水流道和出水池作为一个整体进行三维造型,并以此为对象开展整体式流动分析,如图1所示。这种方式也称作全流道模拟。在安装轴流泵或导叶式混流泵的低扬程泵站中,这种方式比较常见。针对整体式计算域开展的流动分析可以充分反映各组成部分之间的耦合作用,特别是进水流道出口与水泵进口之间的相互影响[41]。这种方式的缺点是,需要较多的已知条件,前处理和计算工作量都很大。例如,在已知水泵叶片木模图和其他水力尺寸的条件下,需要对整个泵段进行三维造型;在没有水泵木模图时,需要以FAN模型[20]的形式引入水泵性能曲线,从而表示泵段的能量阶跃。整体式计算域的边界条件相对简单,除了壁面、水泵转速等基本条件外,通常在进口给定速度条件或总压条件,在出口给定自由出流或静压出口即可。
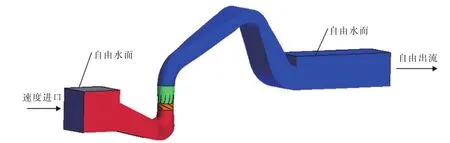
图1 整体式计算域
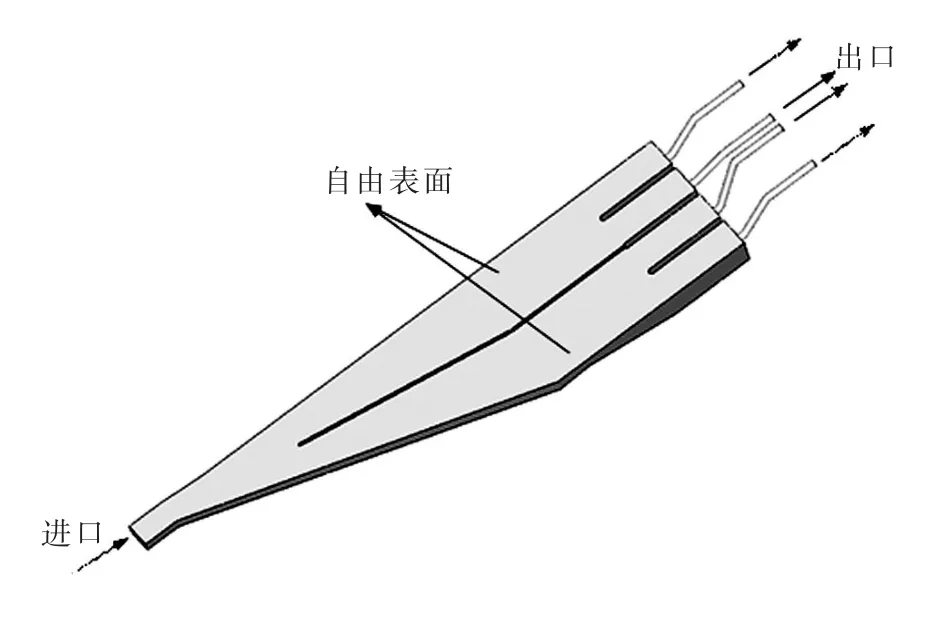
图2 分散式计算域
(2)分散式计算域是对泵站进水系统、泵段和出水系统分别创建实体模型,单独进行流动分析,不考虑各组成部分之间的耦合作用。在给定计算域的进出口边界条件时,需要根据模型试验、现场测试或其他方式估算经验数据。对于低扬程泵站,一般将前池、进水池和进水流道共同组成的对象作为进水系统计算域,将虹吸式出水流道和出水池组成的计算域作为出水系统计算域。对于高扬程泵站,一般将泵站前池、进水池和水泵吸水管共同组成进水系统计算域。图2是南水北调中线工程惠南庄泵站的分散式计算域[42]。该泵站左右对称,各安装4台双吸离心泵,故以中间对称面为分界线,选择右侧一半区域进行计算域造型,计算域只包含了进水系统。
分散式计算具有操作简便、占用计算机资源小、计算速度快等特点,缺点是没有考虑泵站各组成部分之间的耦合作用,如进水流道出口与水泵进口的相互影响。这种方式过去曾广泛使用[43-44],直到今天,如果关注焦点只是泵站进水池流态,则这种方式仍然不失为一种合理选择[45]。但是,随着计算机处理能力的提高,泵站流动分析更多地采用整体式,这一方面是出于计算精度的考虑,更多地是出于泵站瞬态特性,特别是压力脉动等分析的需要。
在构建计算域时,经常需要采用切割或延伸的方式对物理空间进行改造。例如,图1所示的整体式计算域,只将1台机组的进水池纳入,没有包含前池和其他机组对应的进水池。如果流动分析的重点在于前池流态,则不能这样处理。文献[46]针对吉林引松供水工程冯家岭泵站构造了整体计算域,将泵站引水隧洞、封闭式吸水罐、4根水泵吸水管、4台双吸离心泵全部纳入计算域,这样得到的计算结果能更加充分反映泵站各组成部分之间的相互影响,特别是在分析边机组与中间机组的流态区别时更加有用。另一方面,为了在边界上施加均匀速度进口或出流边界条件,避免因计算域不足而导致不合理的解,通常将进口和出口物理边界适当向外延伸,如图1和图2所示的计算域,均进行了延伸。
2.3 网格模型
(1)网格类型。在分散式流动分析中,前池、进水池、进水流道、出水流道等的几何形状相对简单,故多采用结构化网格模型,网格单元以六面体为主。在过去采用有限差分方法求解泵站流动的阶段,结构化网格模型是唯一的网格模型。随着有限体积法的应用,计算域复杂程度不断增加,特别是在泵站整体式流动分析中,涉及水泵叶片等复杂结构,现在多用适应性较强的非结构化网格模型,网格单元主要以四面体为主[42]。为了兼顾计算精度和网格生成难度,有时将结构化网格与非结构化网格混合使用。图3是南水北调中线工程惠南庄泵站的组合式网格,在进水池前端和吸水管部分采用了基于六面体单元的结构化网格,在进水池与吸水管连接区域采用了基于四面体单元的非结构化网格。

图3 高扬程泵站前池与进水池计算网格
在非结构化网格中,虽然四面体单元简单易用,但每个单元只有4个相邻单元,在使用线性插值函数计算单元中心的变量梯度时精度较低,因此,近年出现了多面体单元[40]。在多面体单元组成的网格中,每个单元有多个相邻单元,可以更高精度来逼近梯度,并且同样拥有简单快速的特点。图4是采用多面体单元生成的泵站网格模型。根据文献[40]的研究,在同样的表面网格尺度下,多面体单元网格中单元数量一般只有四面体单元网格的1/4,计算所需内存少,计算效率高。如STAR-CCM+等软件现在多采用这种网格模型来进行网格划分。
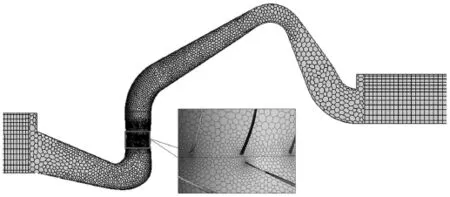
图4 由多面体单元生成的泵站计算网格
(2)近壁区网格参数y+近壁区的流动雷诺数较低,需要采用比主流区更加细密的网格。表征近壁区网格质量的重要参数是y+,按下式定义[12]:

式中:Δy为第一层网格节点到壁面的距离;uτ为壁面摩擦速度;ν为水的运动黏度。
y+体现了网格在近壁区的精细程度,过大或过小的y+都有可能与所使用的湍流模型发生矛盾,不同的湍流模型对y+范围有不同要求[8-10]。以泵站流动分析常用的k-ε湍流模型为例,y+原则上应处于30 ~ 500之间[12,20],如不加特别处理,许多网格模型将有大量区域的 y+超过 1000[47],这时泵站流场计算结果的精度很难保证。另一方面,由于前池、进水池、水泵吸水管等各部分尺度相差较大,形状特征变化较快,导致流场速度梯度与压力梯度也存在较大差异,很难生成各个区域均满足30<y+<500要求的近壁区网格,即使通过精细处理得到这样的网格,则需要花费大量时间。为此,资丹等[47]提出了一种泵站流场y+生成策略,可较方便地生成满足不同y+要求的近壁区网格,图5是专门为k-ε湍流模型生成的泵站前池和进水池计算网格和相应的y+分布,y+基本落在30~500之间。
2.4 数值离散模型在使用有限体积法进行泵站流动分析时,需要在空间域和时间域分别对控制方程进行离散,从而生成数值离散模型。数值离散模型的核心是离散格式,离散格式对离散化方程组的求解精度、效率和稳定性均有重要影响。
2.4.1 空间离散格式 泵站水流速度并不很高,一阶迎风格式[9]被经常用作泵站空间离散格式。这种离散格式最大特点是计算快速、稳定、收敛性强,在早期泵站流动分析中应用比较广泛。二阶迎风格式[9]引入了上游更多节点的物理量,计算精度高于一阶迎风格式,但存在迎风格式固有的假扩散问题。中心差分格式取上、下游节点的算术平均值作为当前节点的值,具有二阶精度,在不发生振荡的参数范围内,可以获得准确计算结果,是当前泵站流动计算中使用最为广泛的离散格式。QUICK格式和MUSCL格式[20]属于三阶精度离散格式,理论上可以减少假扩散,精度较高,但只有在使用六面体结构网格时才能发挥优势。总体而言,高阶格式给出更高的计算精度,但很可能带来计算收敛性的下降。一阶格式的计算精度较低,但计算效率高,计算收敛性往往优于高阶格式。对于实际泵站的流场计算,可先尝试选择二阶格式,如果遇到收敛性问题,改换为一阶格式。或者,先采用一阶格式计算若干迭代步后,改换为二阶格式。
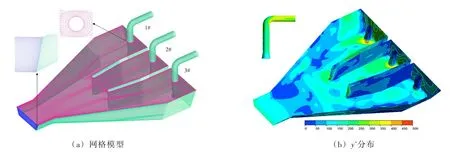
图5 泵站网格模型及相应y+分布
2.4.2 时间离散格式 在进行瞬态问题求解时,要进行时间离散,以实现对差分方程的时间积分。常用的时间离散格式包括一阶格式和二阶格式两种。一阶格式根据本时步和前一个时步的参数来插值,二阶格式增加了前一个时步之前时步的参数。一般来讲,采用一阶格式可以应对大部分泵站流动分析问题。
在进行物理量时间积分时,除了阶数之外,还涉及隐式与显式两种积分方案。在隐式方案所确定的离散方程组中,各未知量耦合在一起,每个时步都需解耦合线性方程组。显式方案只借助当前值和旧值来估计物理量的值,不需解耦合方程组,计算效率高,但时间步长受到限制,不像隐式方案那样稳定。理论上来讲隐式方案无条件稳定,无论时间步长多大。在隐式方案的基础上,近年还出现了有界二阶隐式方案(Bounded Second Order Implicit,BSOI)[20],引入了前后共5个时步的计算结果。相比于普通的二阶方案,BSOI使算法变得更加稳定,在泵站流场计算时应优先采用,但不能用于包含泥沙或空化的多相流计算。
2.4.3 时间步长 时间步长的大小对瞬态问题的计算精度和计算效率有直接影响,是瞬态问题最需要控制的基本参数。时间步长分为固定步长和变步长两种,出于简化计算的目的,泵站流动分析多使用固定步长。采用隐式或显式积分方案,对时间步长的要求有所不同。
(1)隐式方案应保证时间步长小于所求解问题的最小时间常数的一个量级,即比特征长度(如泵站压力管道长度)除以特征速度(如平均速度)的值小一至两个量级。文献[20]认为这样确定的时间步长过小,计算量过大,建议采用最小网格长度除以流速来确定时间步长的方式。判断时间步长是否合适的最好方法,是观察在每个时间步内达到收敛时的迭代次数,理想迭代次数应该为5~10[48]。如果迭代次数较多,则说明这个时间步长过大,应该减小。检验时间步长合理性的具体方法是:在计算进行到一定阶段或全部完成后,绘制整个计算域内的库朗数分布图,库朗数应该不超过20~40。
(2)对于显式方案,时间步长不能太大,否则将出现算法稳定性问题。可按Courant-Fredrichs-Lewy条件来确定显式计算的时间步长[20]:

式中:Δt为时间步长;C为库朗数;V为网格单元体积;Af为单元第f面的面积;为单元第f面的局部特征值中的最大值。一般来说,随着库朗数从小到大变化,收敛速度逐渐加快,但是稳定性逐渐降低。在实际计算时,需要先选择较小的库朗数,依据迭代残差的收敛情况,确定是否需要增大库朗数。
一般而言,对于带有泵段的泵站流动计算,可根据周期性的时间尺度来选择时间步长。将水泵每个叶片通过周期用20~30个时间步来计算,叶片数少时取大时间步数。例如,叶片数是5时,可用总共150个时间步来模拟叶轮旋转一周的运动,即一个时间步对应叶轮在圆周方向旋转2.4°。
2.5 解算模型由于离散后的控制方程组中压力与速度是耦合在一起的,因此,对方程组的求解方法包含耦合式解法和分离式解法两种[9]。耦合式解法同时求解动量方程与连续方程,要求计算网格较精细,对计算机内存等资源要求较高;分离式解法按先后次序分开求解动量方程和连续方程,对网格和计算机内存要求较低,是泵站流动分析的首选方法[20]。
为了将压力与速度间的耦合分解开来,还需要使用压力-速度耦合算法。最早的压力-速度耦合算法是 SIMPLE(Semi-Implicit Method for Pressure-Linked Equations)[14],后来经过改进出现了 SIM⁃PLEC[14]。SIMPLEC更加容易收敛,是目前泵站稳态流动选择最多的算法。PISO(Pressure Implicit with Splitting of Operators)[9]比SIMPLEC增加了一个修正步,使动量方程和连续方程可以得到更好地满足,因此在泵站瞬态流动分析,特别是含有泵段的全流场计算中得到更加广泛应用。FSM(Fractional Step Method)[49]采用算子分裂数学方法将动量方程从连续方程中解耦,相比于PISO算法,计算效率更高,但对包含泵站进水池自由表面的多相流计算,FSM不如PISO稳定。
3 泵站内部流动分析方法的应用
3.1 进水池表面旋涡分析及控制泵站进水池表面旋涡分为自由表面旋涡和次表面旋涡[50-51]。自由表面旋涡源于进水池自由水面,呈开放漏斗状或连贯涡束状,从自由水面一直延伸到水泵进水喇叭口;次表面旋涡源于壁面,从池壁延伸到水泵吸水喇叭口,呈连贯涡带状,也称为附壁涡或附底涡。表面旋涡很可能将空气泡或杂物带入水泵吸入口,从而导致水泵进口出现预旋,叶轮载荷不平衡,造成水泵效率下降,振动增大[52]。美国辛辛那提大学Rajendran和Patel研究组[53-54]被认为最早对泵站表面旋涡进行系统研究。他们利用染色法研究了表面旋涡演化规律,给出了六类自由表面旋涡特征演化过程[53],被美国泵站进水池设计标准[50-51]所采纳。
近年针对表面旋涡的数值模拟有了快速发展。较早的表面旋涡数值模拟基于稳态RANS模型,后来逐渐发展到基于瞬态RANS模型[41,55]。考虑到表面旋涡的非定常特性,Tokyay等[52]认为,借助非扩散LES求解器和精细网格能够捕捉表面旋涡更多细节。为了解决LES对计算资源要求较高的问题,Schneider等[56]提出了一种将格子玻尔兹曼方法(Lattice Boltzmann Method,LBM)与LES相结合的表面旋涡计算方法,在保证计算效率的同时,也得到了比较满意的结果。另一方面,传统的表面旋涡计算,以单相流为前提,在进水池表面引入对称面假定,即“刚盖假定”,可以获得与实际相接近的旋涡形态,且计算效率高。图6是丛国辉[19]采用这种方法计算得到的进水池次表面旋涡。但这种方式无法模拟进水池水面波动,也不能计算水泵启停过程中水面瞬态变化。近年表面漩涡开始采用气液两相流模型来计算[41,56-57],多位学者[58-59]利用 VOF(Volume of Fluid)模型对进水池模拟后发现随机扰动使表面旋涡向非对称、高强度的方向发展,这是单相流计算很难捕捉到的。
在采用VOF模型进行自由表面旋涡计算时,除水体域外,还需要选择自由水面上的一部分空气进入计算域,通常在进水池进口给定总压条件,在水泵吸水管出口给定静压条件或流量条件。自由表面旋涡的运动受角动量守恒定律支配,且具有强迫涡和自由涡的双重特点,在径向和轴向均存在较大的压力梯度,其旋度和涡带直径取决于雷诺数、弗劳德数和韦伯数[60]。
为了消除表面旋涡对水泵吸水管进口流动的影响,近年对消涡装置的研究得到了较大发展[3]。例如,Kim等[61]设计的平面消涡板和十字消涡板有效抑制了水泵吸水喇叭口原有的附壁涡,如图7所示。资丹等[62]将十字消涡板与复合式导流墩结合一起,消除了广东永湖泵站进水池存在的多尺度旋涡,经现场测试,水泵振动由D区减小到B区/A区。成立等[63]采用Y型导流墩、于永海等[64]采用压水板、刘梅清等[65]采用不均匀分布的三角墩分别对大流量低扬程泵站前池中的控涡技术进行了研究,实测证明提高了泵站装置效率。总的来讲,在美国、荷兰等国,横置或竖置的三角墩应用较普遍[66],在韩国、中国等亚洲地区,导流墩与隔板的组合型式应用较广泛[61-62]。
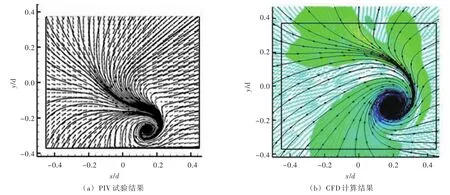
图6 进水池中的次表面旋涡

图7 平面消涡板和十字消涡板技术设施
3.2 泥沙与空化特性分析我国大部分河流都含有泥沙,如黄河沿线泵站的过泵泥沙浓度通常可达30 kg/m3,有时还因泵内吸入空气或空化造成水中含有气泡,对这类多相流问题的模拟,目前有宏观层次模拟方法和介观层次模拟方法两大类。
3.2.1 宏观层次模拟方法 将多相流中的水看作是连续相,由Navier-Stokes方程组所控制,在计算中采用欧拉坐标系描述;将另一相(泥沙颗粒或空化汽泡)看作拟连续相或离散相,由Navier-Stokes方程组或单颗粒运动方程组所控制,采用欧拉坐标系或拉格朗日坐标系描述。这样,就出现了与之对应的欧拉-欧拉方法和欧拉-拉格朗日方法两个分支[20]。
(1)欧拉-欧拉方法是目前泵站泥沙两相流和空化两相流计算的主要方法。在泵站泥沙颗粒直径比较小,特别是悬移质泥沙占据主导时,这种方法的优势比较明显。在水泵空化分析中,也多采用这种方法。欧拉-欧拉方法通常包括3个典型的模型:VOF模型、混合模型和欧拉模型。在CFX等软件中,上述3种模型分别被称为自由界面流动模型、混合模型和粒子模型[23]。其中,VOF模型[67]是一种应用于固定欧拉网格的表面跟踪方法,不同的流体组分共用一套动量方程,泵站空化模拟、进水池表面流动模拟及吸水喇叭管吸入空气模拟等,均可采用这种模型。混合模型求解混合物的动量方程,通过相对速度来描述离散相,是目前水泵与泵站泥沙两相流应用最广泛的多相流模型之一[68]。欧拉模型针对多相流中每一相均建立一套动量方程和连续方程组,通过压力项和界面交换系数来实现耦合。王晓升等[69]利用欧拉模型模拟了泵站虹吸式出水管虹吸形成过程气液两相流,建立了水力驱气阶段和水力挟气阶段分别用不同幂函数表达的时间与流量关系。
在欧拉-欧拉方法中,相间阻力系数是反映固液两相之间作用的主要参数,泥沙扩散系数是反映固相湍动特征、影响固相浓度分布和输移的重要参数。Wen-Yu模型是目前最常用的相间阻力模型[20],其阻力系数由单个刚性球体在静止流体中匀速运动的试验得到。张自超等[70]提出了一种改进的Wen-Yu模型,通过引入湍流修正函数体现了湍流强度对颗粒运动的影响。对于泥沙扩散系数的计算,目前多采用类比水流涡黏系数的泥沙扩散系数半经验模型,代表性的模型主要有NON-DC模型和Diffusion-in-VOF模型[71]。这两个模型均忽略了悬移质颗粒与含能涡相互作用对颗粒周围湍流结构的影响,文献[71]提出了一种改进的泥沙扩散系数模型DC-PDPC,建立了流体湍流强度改变率与粒径、浓度的关系,体现了颗粒动态尺度引起的周围流体湍流结构变化对颗粒运动的影响,在黄河泵站上的应用取得了较好效果,有效预测了泵站泥沙磨损情况[68]。
(2)欧拉-拉格朗日方法将泥沙颗粒运动由拉格朗日坐标系描述。经典的单颗粒动力学模型和颗粒群轨道模型都属于欧拉-拉格朗日方法的范畴。在当今的商用CFD软件中,两者已经合并,一般称为“颗粒轨道模型”[20]。对于液相和粒子的相互作用,有单向耦合和双向耦合两种模式。单向耦合是只考虑流场对粒子的影响,不考虑粒子对流场的影响;双向耦合是同时考虑流场与粒子的双向影响。欧拉-拉格朗日方法假定固相稀疏,因此一般忽略颗粒-颗粒间的相互作用。该方法的最大优势是可以比较方便地计算出每个颗粒的速度、轨迹线等,这对于泥沙磨损分析非常有利,劣势是粒子的整体数量受到限制,只能处理浓度很低的两相流。在早期的泵站泥沙两相流理论分析和计算中应用广泛,目前仍是低泥沙浓度、大颗粒泥沙两相流分析的主要手段之一。
3.2.2 介观层次模拟方法 在宏观和微观之间的介观尺度上研究多相流,代表性方法是LBM方法。在泵站多相流计算中虽不如宏观层次模拟方法应用广泛,但近几年有了比较大的发展。例如,Tang等[72-73]基于LBM和LES耦合思想,建立了二维浅水LBM-BGK模型和泥沙数学模型的联合模式,据此对泵站前池内的水沙流进行了数值模拟,成功预测出前池水沙流速分布、旋涡位置及尺寸,以及泥沙的冲淤变化,揭示了前池大回流区和死水区与泥沙淤积的关系。
对于泵站空化(汽蚀)计算,目前主要有界面追踪法和均相流方法,均属于欧拉-欧拉方法的范畴。早期空化计算以界面追踪法为主,前述VOF模型就是界面追踪法的一种。界面追踪方法更适合计算具有明显空泡边界的片状空化等现象。均相流方法[74]将单流体模型同时应用于汽液两相,而汽液两相间的质量转换通过输运方程实现,常用模型包括基于状态方程的空化模型[75]和基于组分输运方程的空化模型[76]。基于组分输运方程的空化模型又可以分为两类:一是直接给定描述水汽生成和扩散行为显式表达式的空化模型,二是以简化的Rayleigh-Plesset方程为基础的空化模型。目前用于泵站的空化模型多建立在描述空泡动力学特性的Rayleigh-Plesset方程基础上。据此方程,推导出空化相变机制,通过不同的蒸发、凝结项描述相间质量转换率,从而形成不同的空化模型,如Zwart等[77]提出的ZGB空化模型,Singhal等[78]提出的全空化模型,Schnerr等提出的精确Schnerr-Sauer空化模型[79]。近年有人针对热力学效应、旋转效应等对空化模型进行了改进[80-81],使均相流方法成为目前泵站空化计算最为广泛的方法,可有效预测内部空化区域大小,计算水泵空化余量。
3.3 水力激振特性分析泵站机组振动及泵房结构振动多是因流固耦合问题所造成,激振力主要来自泵内或管道内水压力脉动。常用的数值求解方法包括弱耦合和强耦合两种。弱耦合方法将流场和结构场的控制方程分别在时间和空间上单独进行求解,耦合作用不同步;强耦合方法将流场和结构场的控制方程置于同一个封闭方程组系统中,同时离散,在一个时间步内同时求解[82]。由于流场求解多以有限体积法为主,结构场求解多以有限元法为主,二者在算法格式及计算程序上存在较大差异,因此,对于泵站流固耦合问题,目前多采用弱耦合方法求解。
弱耦合方法又分为单向耦合和双向耦合两种。(1)单向耦合过程中,流场分析结果传递给结构场,但不将结构场分析结果传递给流场,即只考虑流场对结构场的影响。这种方法在有些文献中称为动力时程法[83]。目前国内的泵站结构振动分析多采用这种方法,能够比较准确地预测结构振动的频率和幅值,为泵站安全稳定运行提供了技术支持。(2)双向耦合分析将流场分析结果传递给结构场,又将结构场分析结果传递给流场。双向耦合分析的精度理论上高于单向耦合分析,但效率远低于后者。对于双向耦合分析,通常有顺序求解和同步求解两类。对于顺序求解,在一个时间步内,流场与结构场分别先后进行迭代求解,而同步求解要求在一个时间步内同步进行流场与结构场迭代计算。同步求解需要更大的计算机资源,故对复杂流固耦合问题,应用不如顺序求解更普遍。水泵在工作过程中,叶轮和泵体等结构部件的变形基本都在线弹性范围内,变形量往往只有叶轮直径的千分之一量级[84],在流固耦合分析时不计结构变形对流场影响所得到的结果在工程上是可以接受的,因此,大型泵站流固耦合问题目前多采用单向耦合分析模式。当然,随着计算机容量及处理速度的提高,特别是并行计算手段的普及,对水泵及泵站进行双向耦合分析是发展趋势。
流场与结构场间的耦合界面数据传递,是耦合问题求解成功的关键。对于复杂流固耦合问题,流场和结构场的网格在耦合界面上并非一一对应,流场与结构场之间的数据传递,要依靠profile pre⁃serving插值法或globally conservative插值法[85]。前者属于主动询问式传递,后者属于被动式传递。在传递参数时,前者相对简单,后者可保证在全部界面上数据的总体守恒。泵站和水电站流固耦合问题,多采用后者。
为了预测泵站系统可能存在的共振或拍振及其振幅,需要考虑水泵转子或其他水下结构在水中的固有模态和阻尼特性[86]。借助有限元方法已能够比较准确地计算出结构在水中的湿模态,一般来说,结构在水中的固有频率要低于在空气中的固有频率,不同阶次下降的幅度不一致。借助双向流固耦合方法已经可以初步预测水下结构的水力阻尼特性,从Monette等[87-88]的研究看,水力阻尼特性不仅依赖于绕流速度,同时受结构形式及其振型的影响。
通过流固耦合计算获得结构的位移、振动和动态应力后,需要对水泵转子、泵体、水泵梁、泵房楼板等主要结构进行疲劳特性分析。疲劳特性分析模型主要有累积损伤模型和剩余强度模型[85]。累积损伤模型基于累积损伤理论、应力幅值及循环次数的统计分布,得到疲劳寿命的统计参数;剩余强度模型通过对结构剩余强度在疲劳载荷下随时间变化规律的研究,求出其寿命参数。两种模型均可用于泵站疲劳寿命分析,分析过程也大体相同,核心环节是结构应力载荷谱编制和材料疲劳性能确定。其中,应力载荷谱编制的方法主要是雨流读数法,首先根据流固耦合计算得出不同时刻结构动应力,接着用二维应力概率密度函数来描述应力均值和应力幅值的联合分布,最后考虑泵站各种可能运行工况的权重系数求得多工况下复合应力概率密度函数。获得材料疲劳性能的方法,是通过试件试验结果确定材料的P-S-N(可靠度-应力幅值-寿命)曲线。这样,根据得到的应力载荷谱和材料疲劳性能,采用累积损伤模型或剩余强度模型计算出结构寿命。杨魏等[89]据此预测了惠南庄泵站水泵结构的疲劳特性,并在此基础上制订了不同工况下水泵组合运行方式。
3.4 水力瞬变特性分析泵站水力瞬变是系统稳态流动平衡被短时间内发生的流动变化所打破后伴随出现的流速和压力剧烈波动的现象。现有水力瞬变分析方法基本属于一维水力学范畴,即求解对象是一维连续方程和运动方程,这与三维CFD有一定区别。
水力瞬变理论分为刚性水柱理论和弹性水柱理论两大类[2]。刚性水柱理论假设管道内水体作为整体进行加速和减速运动;弹性水柱理论考虑了水体弱可压性和管壁弹性作用,认为水压力变化是按300~1400 m/s的波速传播的,可以更为准确地模拟管道内水流的内部动态特征[2]。现有的水力瞬变分析方法多是在Wylie和Streeter[7]提出的特征线法基础上,引入弹性水柱理论而形成的。自1990年代以来,随着气液两相流、空穴率、变波速和水柱分离等概念的提出,泵站瞬变流分析模型有了很大发展[90],其中最具代表性的成果是波特性法。Wood等[91]通过追踪水锤波的发生、传播、反射和干涉,在保证计算精度不变的前提下,简化了特征线当中瞬态压力值的计算,建立了波特性法,并在此基础上研制成功PIPE2010系列软件,成为当今国内外泵站领域使用最广泛的水力瞬变分析软件之一。
近几年来,为了解决传统特征线法只能在一维空间求解水力瞬变问题的弊端,有学者开始研究一维/三维耦合水力瞬变分析方法,即把一维特征线法与三维CFD法结合在一起,用于分析大口径蝶阀、大流量低扬程水泵末端等三维空间在水力瞬变发生时的流态[92]。
为了评价泵站水锤防护效果,针对空气阀、压力波动预止阀和空气罐等装置计算模型的研究越来越多[93],依靠CFD技术可实现对水泵Suter曲线的仿真[94],泵站水力瞬变分析能力得到显著提高。
3.5 泵站优化水力设计在CFD技术被引入泵站流动分析之前,泵站水力设计属于基于经验的一维水力设计,总体上是按标准规定的原则选取相关结构型式和参数,我国执行的标准是《泵站设计规范》(GB50265)[95],美国执行的标准是《American National Standard for Pump Intake Design》(ANSI/HI9.8)[50-51]。对于相对重要的泵站,辅以物理模型试验,协助确定有关参数和尺寸。
自三维黏性湍流数值模拟成为泵站流动分析主要手段后,泵站水力设计进入到了三维优化设计阶段[11]。在这个过程中,首先根据水力性能和工程投资,参考设计规范,通过一维水力设计手段初定泵站大体轮廓和主要控制尺寸,然后利用CFD技术,以水力损失最小、流速分布均匀等为目标,借助一定的优化算法对初定的过流尺寸进行优化。三维优化设计可以得到直观的流场结构,从而找出影响流态的关键因素,最终获得优选方案。
前池和进水池是泵站水力设计的主要对象,设计目标是保证前池和进水池没有大尺度旋涡,特别是没有被吸入到进水喇叭口的旋涡,池内水力损失小。为此,在保证前池扩散角等基本尺寸符合设计规范的前提下,需要增设立柱、底坎和导流墩等控涡设施。在泥沙含量较高的场合,还需要考虑泥沙沉积对前池的堵塞。现有CFD技术已能够比较准确地预测进水池旋涡分布,校核设计尺寸。对于进水池的水流在进入水泵之前的流态,相关学者提出了一些考核指标,如进水流道出口或进水管道出口断面流速均匀度和偏流角规定如下[2,11]:
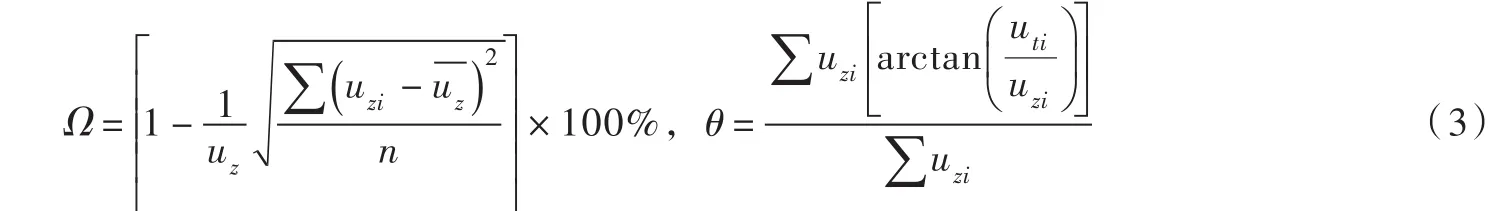
朱红耕等[96]将上述泵站三维优化设计方法应用于南水北调东线工程低扬程泵站设计,优化后使进水流道出口流速均匀度提高3.26%,偏流角减小1°,水力损失减少24.1%。资丹等[97]基于响应面模型,以吸水喇叭管悬空高、后壁距和淹没深度为设计变量,对泵站进水池参数进行优化,优化后流速均匀度提高5.92%,涡量特征值降低3.1倍,显著改善了进水池的流态。
4 结论与展望
近年来,泵站流动分析方法研究取得了长足进步。本文总结了国内外部分专家取得的初步成果,但由于泵站流动分析涉及多方面复杂因素,仍有许多关键科学技术问题需要深入研究并加以解决,建议未来从如下几个方面开展研究:(1)悬移质与空化联合作用条件下泵站气液固多相流理论与算法研究;(2)前池与进水池表面旋涡与水泵运行稳定性关系研究;(3)前池低水位、水泵小流量工况运行时的泵站系统流态研究;(4)空气阀、压力波动预止阀和主控阀等常规水锤防护设备的数学模型研究;(5)高扬程大流量泵站水力瞬变的一维/三维耦合分析方法研究;(6)泵站全工况瞬态流固耦合并行算法研究;(7)基于CFD技术的泵站现代设计方法与设计标准研究。
基于上述认识,笔者建议通过多学科交叉,建立综合考虑水力、结构、环境与工程的泵站流动分析体系,为大型泵站的优化设计和高效稳定运行提供科学依据和技术支持。
[1]中国水利学会泵及泵站专委会.水泵与水泵站学科发展报告[R].北京:中国水利学会,2017.
[2]JONES G M,SANKS R L.Pumping station design[M].3rd edition.Woburn:Butterworth-Heinemann,2008.
[3]KIM C G,KIM B H,BANG B H,et al.Experimental and CFD analysis for prediction of vortex and swirl angle in the pump sump station model[C]//International Symposium of Cavitation and Multiphase Flow,ISCM 2014,Bei⁃jing,China,2014.
[4]FOCKET A D,WESTENDE J M C V,VERHAART F I H.Automatic swirl angle measurements for pump intake design[J].Journal of Hydraulic Research,2015,53(3):384-393.
[5]KIM E,PALAZZOLO A.Rotordynamic force prediction of a shrouded centrifugal pump impeller-part 1:numer⁃ical analysis[J].Journal of Vibration and Acoustics,ASME,2016,138(3):031014.
[6]KELLER R.Investigation of severe water hammer in a large pump station-case study[C]//Proceedings of the Pipe⁃lines 2014 Conference,Oregon,Portland,2014.
[7]WYLIE E B,STREETER V L,SUO L S.Fluid transients in systems[M].Englewood Cliffs:Prentice Hall,1993.
[8]HIRSCH C.Numerical computation of internal and external flows:fundamentals of computational fluid dynamics[M].2nd edition.Butterworth-Heinemann,2007.
[9]VERSTEEG H,MALALASEKRA W.An introduction to computational fluid dynamics:the finite volume method[M].2nd edition.Prentice Hall,2007.
[10]MOUKALLED F,MANGANI F,DARWISH M.The finite volume method in computational fluid dynamics:an advanced introduction with OpenFOAM and Matlab[M].Springer International Publishing,2016.
[11]陆林广.高性能大型低扬程泵装置优化水力设计[M].北京:中国水利水电出版社,2013.
[12]王福军.计算流体动力学分析——CFD软件的理论与应用[M].北京:清华大学出版社,2004.
[13]王福军.流体机械旋转湍流计算模型研究进展[J].农业机械学报,2016,47(2):1-14.
[14]PATANKAR S V.Numerical heat transfer and fluid flow[M].Washington:Hemisphere,1980.
[15]SPALART P,ALLMARAS S.A one-equation turbulence model for aerodynamic flows[R].AIAA Paper 92-0439,1992.
[16]LAUNDER B E,SPALDING D B.Lectures in mathematical models of turbulence[R].Academic Press,Lon⁃don,1972.
[17]YAKHOT V,ORZAG S A.Renormalization group analysis of turbulence:basic theory[J].Journal of Scientific Computing,1986,1(1):3-11.
[18]SHIH T H,LIOU W W,SHABBIR A.A new k-e eddy viscosity model for high Reynolds number turbulent flows[J].Computers and Fluids,1995,24(3):227-238.
[19]丛国辉,王福军 .湍流模型在泵站进水池漩涡模拟中的适用性研究[J].农业工程学报,2008,24(6):31-35.
[20]Ansys Inc.Ansys FLUENT theory guide[M].Southpointe:Ansys Inc.,2017.
[21]Wilcox D C.Multiscale model for turbulent flows[C]//AIAA 24th Aerospace Sciences Meeting.American Insti⁃tute of Aeronautics and Astronautics,1986.
[22]MENTER F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal,1994,32(8):1598-1605.
[23]Ansys Inc.Ansys CFX-solver theory guide[M].Canonsburg:Ansys Inc.,2017.
[24]GATTORONCHIERI A,CRAVERO C,DE FRANCO L.The application of CFD to vortical flow structures detec⁃tion in sea water pumping stations[C]//6th International Conference on Computational Methods in Marine Engi⁃neering,Rome,Italy,June 15-17,2015.
[25]MENTER F R,SCHUTZE J,KURBATSKII K A.Scale-resolving simulation techniques in industrial CFD[C]//6th AIAA Theoretical Fluid Mechanics Conference,2011.
[26]PIOMELLI U.Large-eddy simulation:present state and future directions[R].AIAA Paper 98-0534,1998.
[27]SMAGORINSKY J.General circulation experiments with primitive equations[J].Monthly Weather Review,1963,91(3):99-164.
[28]GERMANO M,PIOMELLI U,MOIN P.A dynamic subgrid-scale eddy viscosity model[J].Physics of Fluids A:Fluid Dynamics,1991,3(7):1760-1765.
[29]NICOUD F,DUCROS F.Subgrid-scale stress modelling based on the square of the velocity gradient tensor[J].Flow Turbulence and Combustion,1999,62(3):183-200.
[30]SHUR M L,SPALART P R,STRELETS M K.A hybrid RANS-LES approach with delayed-DES and wall-mod⁃elled LES capabilities[J].International Journal of Heat and Fluid Flow,2008,29(6):1638-1649.
[31]KIM W W,MENON S.Application of the localized dynamic subgrid-scale model to turbulent wall-bounded flows[R].AIAA Paper,AIAA-97-0210,1997.
[32]YANG Z J,WANG F J.A dynamic mixed nonlinear subgrid-scale model for large-eddy simulation[J].Engineer⁃ing Computations,2012,29(7):778-791.
[33]周佩剑,王福军,姚志峰 .离心泵叶轮旋转失速团特性分析[J].水利学报,2015,46(9):1128-1134.
[34]LI Y,MENEVEAU C,CHEN S Y,et al.Subgrid-scale modeling of helicity and energy dissipation in helical tur⁃bulence[J].Physical Review E-Statistical Nonlinear and Soft Matter Physics,2006,74(2):26310.1-10.
[35]MENTER F R,EGOROV Y.A scale-adaptive simulation model using two-equation models[R].AIAA paper 2005-1095,2005.
[36]MENTER F,EGOROV Y.The scale-adaptive simulation method for unsteady turbulent flow predictions.part 1:theory and model description[J].Journal Flow Turbulence and Combustion,2010,85:113-138.
[37]STRELETS M.Detached eddy simulation of massively separated flows[R].AIAA Paper 2001-0879,2001.
[38]CONSTANTINESCU G S,PATEL V C.Role of turbulence model in prediction of pump intake vortices[C]//ASME Fluids Engineering Division Summer Meeting,Washington DC,USA,1998.
[39]CONSTANTINESCU G.On the use of eddy resolving techniques to simulate river transport processes and flow around hydraulic structures[C]//The US-China workshop on advanced computational modelling in hydroscience&engineering,Oxford,Mississippi,USA,2005.
[40]周佩剑.轴流泵装置进出水流道与泵段水力耦合特性分析[D].北京:中国农业大学,2011.
[41]LOMAKIN V O,KULESHOVAV M S,BOZHEVA S M.Numerical modeling of liquid flow in a pump station[J].Power Technology and Engineering,2016,49(5):324-327.
[42]冯宾春,石维新,谢省宗,等.惠南庄泵站前池水力特性三维紊流数值模拟[J].南水北调与水利科技,2005,3(1):17-20.
[43]刘树红,耿福明,吴玉林,等.大型泵站水泵吸水池中流动稳定性研究[J].南水北调与水利科技,2008,6(1):138-142.
[44]刘超,金燕 .双向流道泵装置内三维流动数值模拟[J].农业机械学报,2011,42(9):74-78.
[45]ZI DAN,WANG FUJUN,YAO ZHIFENG,et al.Numerical simulation on rectifying flow in intake system of a pumping station connected with headrace pipe[C]//28th IAHR Symposium on Hydraulic Machinery and Systems,Grenoble,France,2016.
[46]资丹,田明,邹玉涛,等 .装备封闭式吸水罐的泵站水力学特性[J].排灌机械工程学报,2015,33(9):768-772.
[47]资丹,王福军,陶然,等 .边界层网格尺度对泵站流场计算结果影响研究[J].水利学报,2016,47(2):139-149.
[48]Ansys Inc.Ansys FLUENT user's guide[M].Southpointe:Ansys Inc.,2017.
[49]ARMSFIELD S,STREET R.The fractional-step method for the Navier-Stokes equations on staggered grids:ac⁃curacy of three variations[J].Journal of Computational Physics.1999,153:660-665.
[50]Hydraulic Institute.American National Standard for Pump Intake Design,ANSI/HI9.8-1998[S].New Jersey:Hydraulic Institute,1998.
[51]Hydraulic Institute.American National Standard for Rotodynamic Pumps for Pump Intake Design,ANSI/HI9.8-2012[S].New Jersey:Hydraulic Institute,2012.
[52]TOKYAY T E,CONSTANTINESCU S G.Large eddy simulation and Reynolds averaged Navier-Stokes simula⁃tions of flow in a realistic pump intake:a validation study[C]//2005 World Water and Environmental Resources Congress,Anchorage,US,2005.
[53]RAJENDRAN V P,CONSTANTINESCU G S,PATEL V C.Experimental validation of numerical model of flow in pump-intake bays[J].Journal of Hydraulic Engineering,1999,125(11):1119-1125.
[54]RAJENDRAN V P,PATEL V C.Measurement of vortices in model pump-intake bay by PIV[J].Journa1of Hy⁃draulic Engineering,2000,126(5):322-334.
[55]CONSTANTINESCU G,PATEL V C.Role of turbulence model in prediction of pump-bay vortices[J].Journal of Hydraulic Engineering,2000,126(5):387-391.
[56]SCHNEIDER A,CONRAD D,BOHLE M.Lattice Boltzmann simulation of the flow field in pump intakes:a new approach[J].Journal of Fluids Engineering,ASME,2015,137(3):031105.
[57]QIU Baoyun,CHU Shiji,FENG Xiaoli.Numerical simulation of flow fields and head losses of trash-barriering in pumping station based on VOF model[C]//International Mechanical Engineering Congress and Exposition,2014.
[58]LONG N I,SHIN B R.Study on surface vortices in pump sump[J].Journal of Fluid Machinery,2012,15(5):60-66.
[59]马涛,樊红刚,袁义发,等 .基于VOF模型的泵站进水池流场计算研究[J].水力发电学报,2013,32(6):244-249.
[60]AHN S H,XIAO Y X,WANG Z W,et al.Numerical prediction on the effect of free surface vortex on intake flow characteristics for tidal power station[J].Renewable Energy,2017,101:617-628.
[61]KIM J Y,CHUNG K N,KIM H G,et al.Flow analysis of the subsurface vortices in pump sump models[C]//23rd IAHR Symposium on Hydraulic Machinery and Systems,Yokohama,Japan,2006.
[62]资丹,王福军,姚志峰,等.大型泵站进水流场组合式导流墩整流效果分析[J].农业工程学报,2015,31(16):71-77.
[63]成立,祁卫军,罗灿,等.Y形导流墩几何参数对泵站前池整流效果的影响[J].水利水电科技进展,2014,34(1):68-72.
[64]于永海,徐辉,程永光.泵站前池导流板整流措施数值模拟研究[J].水利水电技术,2006,37(9):41-43.
[65]刘梅清,林琦,梁兴,等.泵站前池流态改善效果的数值模拟分析[J].武汉大学学报(工学版),2012,45(2):152-156.
[66]VERHAART F I H,ZWANENBURG S A A,DE FOCKERT A.The results of a detailed measurement campaign on the effect of modifications to the pump compartment on spatial velocity profiles in vertically submersible pumps[C]//27th IAHR Symposium on Hydraulic Machinery and Systems,Montreal,Canada,2014.
[67]HIRT C W,NICHOLS B D.Volume of fluid(VOF)method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39:201-225.
[68]张自超,王福军,陈鑫,等.基于改进固液两相流欧拉算法的双吸离心泵泥沙磨损特性研究[J].农业机械学报,2017,48(3):124-133,147.
[69]王晓升,冯建刚,陈红勋,等.泵站虹吸式出水管虹吸形成过程气液两相流数值模拟[J].农业机械学报,2014,45(5):78-83.
[70]张自超,王福军,陈鑫,等.低浓度固液两相流相间阻力修正模型研究[J].农业机械学报,2016,47(12):92-98.
[71]张自超,陈鑫,王福军,等.考虑颗粒动态尺度影响的泥沙扩散系数模型建立及应用[J].农业工程学报,2016,32(22):129-137.
[72]TANG Xuelin,WANG Wuchang,WANG Fujun,et al.Application of LBM-SGS model to flows in a pump⁃ing-station forebay[J].Journal of Hydrodynamics,2010,22(2):196-206.
[73]唐学林,王武昌,王福军,等 .泵站前池水沙流的数值模拟[J].排灌机械工程学报,2011,29(5):411-417.
[74]KUBOTA A,KATO H,YAMAGUTI H.A new modelling of cavitating flows:a numerical study of unsteady cavi⁃tation on a hydrofoil section[J].Journal of Fluid Mechanics,1992,240:59-96.
[75]DELGOSHA C O,REBOUD J L,DELANNOY Y.Numerical simulation of the unsteady behaviour of cavitating flows[J].International Journal for Numerical Methods in Fluids,2003,42:527-548.
[76]SENOCAK I,SHYY W.Interfacial dynamics-based modelling of turbulent cavitating flows,part-1:model de⁃velopment and steady-state computations[J].International Journal for Numerical Methods in Fluids,2004,44:975-995.
[77]ZWART P J,GERBER A D,BELAMRI T.A two-phase flow model for predicting cavitation dynamics[C]//Inter⁃national Conference on Multiphase Flow,Yokohama,Japan,May 30-June 4,2004.
[78]SINGHAL A K,ATHAVALE M M,LI H Y.Mathematical basis and validation of the full cavitation model[J].Journal of Fluids Engineering,ASME,2002,124:617-624.
[79]SCHNERR G H,SAUER J.Physical and numerical modeling of unsteady cavitation dynamics[C]//4th Interna⁃tional Conference on Multiphase Flow.New Orleans,USA,2001.
[80]NIEDZWIEDZKA A,SCHNERR G H,SOBIESKI W.Review of numerical models of cavitating flows with the use of the homogeneous approach[J].Archives of Thermodynamics,2016,37(2):71-88.
[81]LUO X W,JI B,TSUJIMOTO Y.A review of cavitation in hydraulic machinery[J].Journal of Hydrodynamics,2016,28(3):335-358.
[82]MORAND H J P,OHAYON R.Fluid-structure interaction[M].John Wiley&Sons,1995.
[83]王新,魏述和.大型泵站的流固耦合振动分析[J].人民长江,2009,40(22):56-59.
[84]JIANG Y Y,YOSHIMURA S,IMAI R,et al.Quantitative evaluation of flow-induced structural vibration and noise in turbomachinery by full-scale weakly coupled simulation[J].Journal of Fluids and Structures,2007,23(4):531-544.
[85]王福军.水力机械流固耦合研究进展与前沿科学问题[M]//张楚汉,王光谦.中国学科发展战略-水利科学与工程.北京:科学出版社,2016.
[86]CHIRAG T.A review on fluid structure interaction in hydraulic turbines:A focus on hydrodynamic damping[J].Engineering Failure Analysis,2017,77:1-22.
[87]MONETTE C,NENNEMANN B,SEELEY C,et al.Hydro-dynamic damping theory in flowing water[C]//27th IAHR Symposium on Hydraulic Machinery and Systems,Montreal,Canada,September 22-26,2014.
[88]LIAGHAT T,GUIBAULT F,ALLENBACH L,et al.Two-way fluid-structure coupling in vibration and damping analysis of an oscillating hydrofoil[C]//Proceedings of ASME International Mechanical Engineering Congress&Exposition,Montreal,Canada,November 14-20,2014.
[89]杨魏,王福军,肖若富,等 .惠南庄泵站机组变频调节运行方案分析[J].水利学报,2015,46(7):853-858.
[90]杨开林.长距离输水水力控制的研究进展与前沿科学问题[J].水利学报,2016,47(3):424-435.
[91]WOOD D J,LINGIREDDY S,BOULOS P F.Pressure wave analysis of transient flow in pipe distribution systems[M].MWH Soft,2005.
[92]WANG X D,DONG J L,WANG T.Numerical study of large diameter butterfly valve on flow characteristics[J].Advanced Materials Research,2011,236/238:1653-1657.
[93]张健,苗帝,黎东洲,等.长距离供水工程空气罐水锤防护方案研究[C]//第二十七届全国水动力学研讨会文集,南京,2015.
[94]王玲,黎珉,王福军,等.用于确定双吸离心泵Suter曲线的三维内特性法研究[J].水利学报,2017,48(1):113-122.
[95]中华人民共和国国家标准,泵站设计规范(GB50265-2010)[S].北京:中国计划出版社,2010.
[96]朱红耕,袁寿其.大型泵站进水流道技术改造优选设计[J].水力发电学报,2006,25(2):51-55.
[97]资丹,王福军,姚志峰,等.基于响应曲面模型的泵站进水池参数优化方法研究[J].水利学报,2017,48(5):594-607.

