基于响应面法的扣索索力优化分析

刘振华，李 成，杨 洋，王德英

（广西交通职业技术学院，广西 南宁 530023）

0 引言

随着拱桥跨径的逐步增大，无支架施工技术在拱桥施工中得到了快速的运用和发展。目前大跨度的劲性骨架拱桥施工普遍采用无支架缆索吊装联合斜拉扣挂法施工。劲性骨架节段标高通过斜拉扣索索力调整来实现，斜拉扣索索力对劲性骨架成拱线性以及成桥拱圈线性影响很大，因此索力的计算和优化就显得尤为重要。

张万晓采用切线坐标修正公式结合ANSYS优化模块求解了钢管混凝土拱桥悬拼过程中的扣索张拉力；张建民等通过修正节点坐标和转角，再利用优化算法来确定扣索张拉力。这些方法计算过程复杂，不易掌握。本文以南盘江大桥（劲性骨架拱桥）为研究对象，把永久扣索作为自变量，将有限元模型分析与响应面法相结合，使劲性骨架合拢拱轴线满足设计要求。

1 基于响应面法扣索索力优化计算流程

大跨度劲性骨架拱桥骨架悬拼过程中，为使拱肋合拢后的线形达到设计标准，需要对各个吊装阶段的扣索索力进行计算。基于响应面的扣索索力求解就是将获得的试验点代入考虑吊装过程的有限元模型当中展开分析，从而获得精准的响应面模型，再对响应展开预测，其求解步骤为：

（1）试验设计。对拱肋合拢线形影响的首要因素为扣索索力，因此选择扣索索力当作设计自变量，拱肋合拢后各控制点的挠度yi以及各控制点挠度平方和y2作为响应值，采用前面叙述的Box－Behnken试验设计方式展开试验设计。

（2）响应值计算。将获得的试验设计数据代入到考虑悬拼过程的有限元模型中，可得到相应的响应值yi和y2。

（3）响应面模型回归。将试验设计数据及响应值代入多项式中，运用最小二乘法机理使试验误差满足精度要求，拟合回归获得响应面模型。

（4）响应面模型精度检验。采取多重拟合系数R2验证拟合模型的准确性，若能达到精度要求，则进行下一步，若不能，需要重新对试验展开设计。

（5）求解扣索索力。将获得的多项式函数作为目标函数，扣索索力的取值范围当作约束条件，采取Matlab中的非线性规划原理计算扣索索力，可获得满足约束条件（拱肋成拱后各控制点挠度的平方和最小）的扣索索力。

2 工程运用实例

2.1 工程概况

以南盘江大桥为工程背景，该桥坐落于云南省丘北县和弥勒县交界的位置，横跨南盘江，全桥长929m，跨径组合为3×42m连续梁＋（60m＋104m＋60m）连续刚构＋416m上承式钢管混凝土拱桥＋2×60mT构＋1×43m简支梁，桥梁总平面图见图1。劲性骨架拱肋由19个悬臂拼装节段和一个合拢段组成，悬拼过程的斜拉扣索采用19组扣索（10组永久扣索，9组临时扣索），骨架分段，斜拉扣索设置见图2。

图1 南盘江特大桥总体布置图（cm）

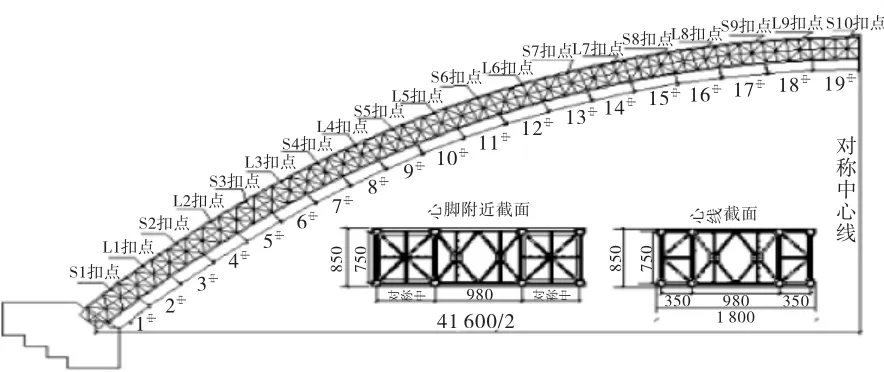
图2 钢管拱肋分段及扣索设置示意图

2.2 试验设计及响应面参数

南盘江大桥骨架悬拼过程中采用19组扣索（10组永久扣索，9组临时扣索）通过参数灵敏性分析可知：临时扣索索力改变对拱肋成拱结构响应相对于永久扣索小许多，因此本文选择S1～S10这10组永久扣索作为试验参数设计变量Si（i＝1，2，…10）。

根据Box－Behnken试验设计安排表各因素的组合，采用有限元软件Midas Civil，代入组合中的数据计算得到了考虑施工阶段拱肋成拱各控制点的位移yi及控制点的平方和y2，通过前面的试验分析结果，采用二次多项式对S1～S10挠度响应值yi及控制点挠度之和y2进行响应面拟合。在拟合过程中，为了保证响应面模型的精度，必须剔除对结构响应不显著的参数。因此，本文采用逐步回归的办法，将试验得到的数据进行回归拟合，从而得到拱肋成拱后挠度的响应面模型（因篇幅有限，本文只列出各扣索张拉力Si与各扣点位移平方和的响应面模型以及部分响应面三维模型，见图3、图4）。

图3 参数S1、S2与y2响应面模型示意图（kN）

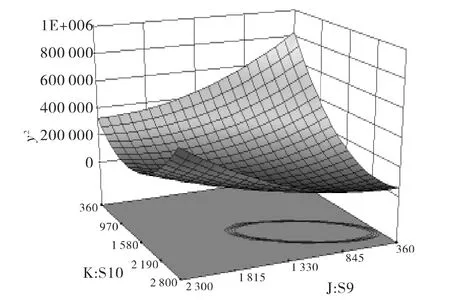
图4 参数S9、S10与y2响应面模型示意图（kN）

控制点挠度平方和：

y2＝2.1＋6－45.6×S2－75.5×S3－38.2×S4－8.2×S5－174.1×S6－355.3×S7－647.8×S8－917.0×S9－1 148.9×S10＋0.02×S4×S10＋8.315 28－3×S5×S10＋0.04×S6×S7＋0.04×S6×S8＋0.02×S6×S9＋0.1×S7×S8＋0.06×S7×S9＋0.03×S7×S10＋0.15×S8×S9＋0.09×S8×S10＋0.2×S10＋0.06×S62＋0.07×S72＋0.1×S82＋0.13×S92＋0.18×S102

2.3 确定扣索索力

将回归获得响应面模型当作目标函数，各扣索索力取值区间当作约束条件，各参数的取值区间通过对扣点进行力学分解确定，构建优化模型见式（1）：

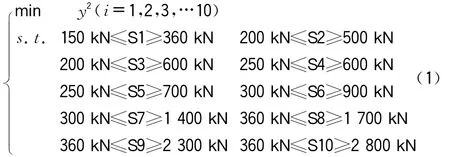
本文采用Matlab优化工具箱非线性规划方法对目标函数进行了优化，获得了满足各控制点在拱肋成拱的位移平方和最小值所对应的各参数的优化值，具体见表1。

由表1可以看出：索力S2最大优化率达到13.5%，优化前后的索力差值为37kN；索力S10优化率最小为1.1%，优化前后的索力差值为3.5kN。由此可见：采用优化算法求解的斜拉扣索索力与优化前的索力有明显变化，这是因为优化算法以拱肋成拱的变形为目标函数，而改进的索力算法以施工过程线形控制为目的，所以两者计算结果差值较大。

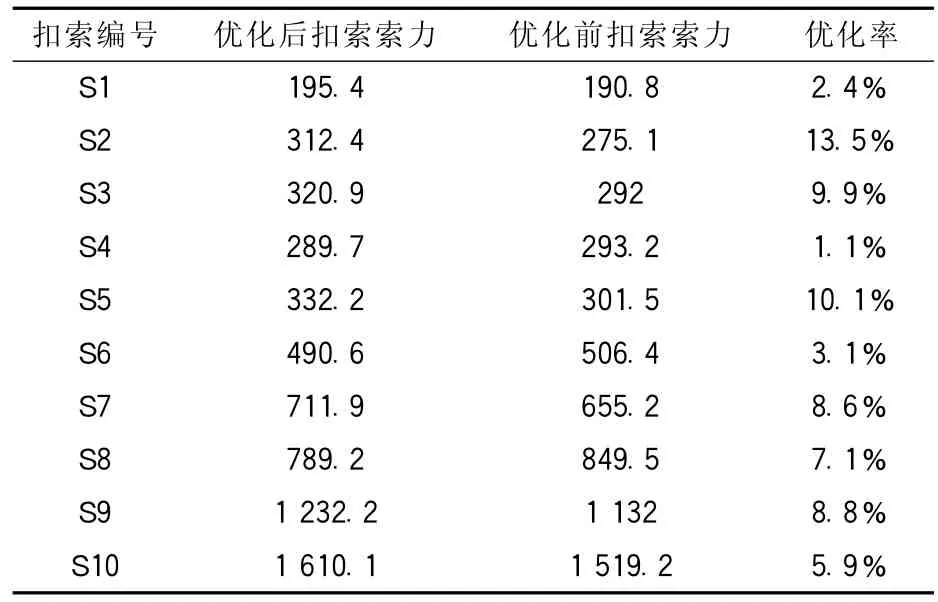
表1 扣索索力表（kN）

2.4 模型验证

为了进一步验证响应面预测的精确性，将优化过后的各扣索索力代入考虑悬拼过程的有限元模型中展开计算获得拱肋成拱各控制点的挠度，与代入回归后的响应面模型中获得的控制点挠度进行对比，见表2。

由表2可以看出：采用响应面模型预测的拱肋成拱后各控制点挠度与有限元模型计算值比较接近，最大差值仅为2.6mm，最小差值只有0.5mm，满足结构响应预测要求。由此可知，通过采用响应面法将扣索索力与结构响应的隐式关系显现化，得到的二次多项式响应面模型能够比较精确地预测结构响应，能够作为优化的目标函数。

表2 预测值和有限元计算值比较表（mm）

2.5 优化前后对比分析

本节将对比分析优化前后拱肋成拱后骨架变形情况。优化前后拱肋成拱控制点变形见下页表3和图5。

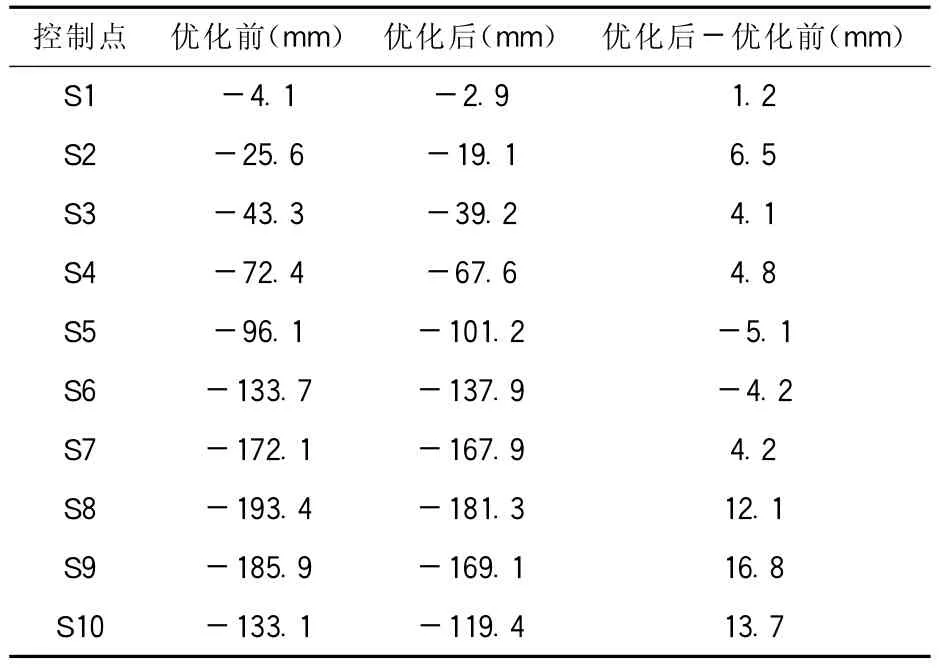
表3 优化前后拱肋成拱控制点变形分析对比表

图5 优化前后拱肋成拱变形曲线图

由表3和图5可以看出：

（1）优化后拱肋在各控制点的变形有明显的变化，S9控制点的拱肋成拱变形减少16.8mm；拱肋成拱变形最小减少1.2mm，发生在S1控制点；总体来讲，优化后拱肋成拱的变形比优化前有明显减少。

（2）优化前与优化后的变形曲线沿拱轴线呈递增趋势，在靠近拱顶位置曲线出现突变，这是由拱肋悬臂拼装过程中张拉斜拉索以及合扰后结构体系转换造成的；优化后的拱肋变形的线形明显优于优化前，且延拱轴线的变形值小于优化前的变形。

3 结语

本文在改进的索力计算方法的基础上，采用响应面法中BOX试验设计，逐步回归拟合出响应面模型，再采用Matlab优化工具箱对S1～S10斜拉扣索索力进行优化计算，得到了以下结论：

（1）响应面法用于劲性骨架拱桥骨架悬拼过程中斜拉扣索索力的求解，将各扣索索力作为自变量，拱肋成拱各控制点挠度作为因变量进行响应面分析，回归得到满足精度要求的响应面模型，响应面模型预测值与有限元计算值相差较小，拟合的响应面模型能够比较精确地预测结构响应，可以作为优化目标函数。

（2）以得到的响应面模型为优化函数，各扣索索力的取值范围为约束条件，采用非线形规划方法求解骨架悬拼过程中的斜拉扣索索力，优化后的拱肋变形线形明显优于优化前，且延拱轴线的变形值小于优化前。