采用权值配比优化的超级电容等效电路模型参数辨识
张乐,续丹,王斌,马光亮,李其玉,周欢
(西安交通大学机械电子工程研究所,710049,西安)
超级电容作为一种新型的储能装置,具有功率密度大、充放电速度快、工作效率高、循环寿命长等优点而受到研究者的广泛关注[1-3]。建立一个能够实时反映超级电容充放电及自放电等特性的模型,对超级电容储能系统的均衡、控制和性能优化等都有重要的意义[4-5]。常见的超级电容模型包括电化学模型和等效电路模型[6-7]。电化学模型能很好地反映超级电容的内部工作机理,但无法反映超级电容的物理特性。等效电路模型采用电阻、电容元件描述超级电容的动态工作特性,具有实际的物理意义,因此具有很强的实用性。由于超级电容等效电路参数辨识的结果直接影响模型精度,因此在建立超级电容等效电路模型的基础上,采用合适的方法对模型参数进行有效辨识显得尤为重要。
目前,超级电容模型参数辨识方法包括最小二乘法、粒子群算法、自适应模糊估计算法、二元二次方程拟合等[8-10]。最小二乘法简单直观,对非线性模型参数具有很好的统计计算效果,但辨识精度不高;粒子群算法能提高模型参数辨识的精度,但计算复杂,特别是对时变系统不易实现在线参数辨识;自适应模糊估计对非线性系统有较好的鲁棒性,但稳态误差难以补偿;二元二次拟合方法求解结果为特定的解,常因虚根问题造成辨识结果不准确。
考虑超级电容的容量随电压变化,还需要辨识超级电容的可变电容分支参数[11-12]。为了采用简单有效的方法辨识超级电容模型参数,本文提出一种基于权值配比优化的超级电容等效电路模型参数辨识方法。基于超级电容三分支等效电路模型,首先通过可变电容和电压之间的关系拟合可变电容的比例参数,然后结合递推最小二乘法(RLS)和双线性变换方法在不同工步条件下参数辨识的优点对模型参数进行修正,以获得更加精确的参数估计值,最后通过等效电路模型计算结果与实验测试结果比较,验证了所提出的基于权值配比优化方法的有效性。
1 超级电容模型
超级电容的等效电路建模具有方法简单、便于计算等优点。已有的等效电路模型包括经典等效电路模型、梯形电路模型、多分支RC模型等[11,13-14]。经典等效电路模型结构简单、参数辨识容易,但在长时间充放电和静置条件下,模型仿真精度不高;梯形电路模型在较宽的频率范围内有较高的拟合精度,但阶次越高,模型精度越高,参数辨识也越复杂,并且梯形等效电路不同分支中的电阻和电容耦合度高,不易求解;多分支RC模型考虑了超级电容电压与电容的依赖关系,各分支上电阻和电容相对独立,可以根据精度要求选择分支数[15]。
本文采用三分支等效电路对超级电容建模,可以有效保证模型精度,并且模型复杂度适中,如图1所示。考虑超级电容的容量随电压变化,在模型第1分支中采用固定电容Ci0和固定电容Ci1与时变电压V的乘积组合而成的“可变电容”Ci1V组成快速分支,采用Ri模拟快速分支等效串联内阻,根据电容随电压的变化关系描述超级电容充放电时的时变动态特性;采用Rd和Cd串联构成慢速分支;采用Rl构成自放电分支,主要描述超级电容在充放电结束后的自放电特性。因此,通过第1、第2和第3分支等效电路设计,可以有效描述超级电容内部电荷的重新分配现象和充放电、自放电等特性。

图1 超级电容等效电路模型
2 参数辨识
在新威尔测试平台上对超级电容进行多工步条件测试。基于超级电容三分支等效电路模型,分别采用RLS法和双线性变换法对模型参数进行辨识。
2.1 递推最小二乘法辨识
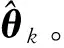
(1)
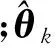
(2)
式中:z(k)为输出量的第k次观测值;y(k-j)是系统第k-j个输出值;u(k-j)为系统的第k-j个输入值;v(k)是系统的测量噪声;αj、βj分别是RLS算法中输出量和输入量的待求解系数。

h(k)=[-y(k-1),…,-y(k-n),
u(k-1),…,u(k-n)]
(3)
(4)
RLS法具体递推算法为
(5)

根据图1所示的超级电容等效电路模型,选择电流i(t)作为系统的输入,电压u(t)作为系统的输出。在超级电容充放电过程中可实时采集得到N个输入值i(1),…,i(N)和N个输出值u(1),…,u(N)。首先,求超级电容模型传递函数
(6)
式中:X=RiRl+RdRl+RiRd,Ri、Rd、Rl分别为模型第1、第2和第3分支的电阻;Ci为第1分支的总电容值;Cd为第2分支的电容;s为拉式变换的复变量。对式(6)进行拉氏变换
G(s)=(b2s2+b1s+b0)/(s2+a1s+a0)
(7)
其中拉氏变换系数a1、a0、b2、b1、b0分别为
(8)
对连续传递函数进行离散化,即对传递函数进行z变换
G(z)=
(9)
相应的差分方程为
u(z)=α1u(z-1)+α2u(z-2)+β1i(z)+
β2i(z-1)+β3i(z-2)
(10)
式中:u(z)为系统输出量的第z次观测值;u(z-n)为系统第z-n次输出值(n=1,2,…);i(z-n)为系统的第z-n次输入值(n=0,1,2,…);α1、α2、β1、β2、β3为RLS算法的待求解系数
(11)
实验输入输出数据矩阵和系统待辩识参数矩阵的z变换分别为
h(z)=
[-u(z-1),-u(z-2),i(z),i(z-1),i(z-2)]
(12)
(13)
式(10)可改写为
(14)

2.2 双线性变换辨识
应用双线性变换方法对超级电容等效电路模型进行参数辨识。通过将由连续信号采样所得的实验数据进行离散化区域划分,对模型的传递函数进行离散化处理,从而实现对模型参数的有效估计。对式(7)进行双线性变换
G(z)=(β3z-2+β2z-1+β1)/(-α2z-2-α1z-1+1)
(15)
相应的差分方程为
u(z)=α1u(z-1)+α2u(z-2)+β1i(z)+
β2i(z-1)+β3i(z-2)
(16)
其中
(17)
采用双线性反变换求实际参数模型得
(18)
即
(19)
3 实验测试和模型计算分析
本文具体研究的双电层超级电容型号规格为SAMWHA 350F。额定电压为2.7 V,在恒流条件下对其进行充放电和自放电实验,电流选择为15 A,实验环境温度为20 ℃,采样周期为1 s。实验所用的新威尔超级电容测试平台如图2所示,实验测试的超级电容单体充放电特性曲线如图3所示。

图2 超级电容测试平台

图3 超级电容单体实验曲线
为确定超级电容等效电容Ci随端电压U变化的函数关系,采用曲线拟合方法对实验所得数据进行处理,有
Ci=Ci0+Ci1V=0.114 8V-0.083 14
(20)
通过电容和电压的拟合曲线得Ci1=0.114 8。
基于可变分支电容比例参数的辨识结果,分别采用RLS法和双线性变换方法对超级电容等效电路模型进行参数辨识,并通过模型计算结果和实验结果验证所辨识参数的准确性,基本思路如图4所示,参数辨识结果见表1。

图4 参数辨识与模型验证流程图

方法Ri/ΩRd/ΩRl/ΩCi/FCd/FRLS0.01250.013930328.586919.1526双线性变换0.01180.017821.31327.298525.1575
分别采用RLS法和双线性变换方法进行参数辨识后获得的超级电容充放电及自放电对应的电压曲线如图5、图6所示。

图5 RLS法计算结果与实验结果比较
由图5可以看出,RLS方法在平稳环境下能有效模拟超级电容的充放电特性,而在非平稳环境下对突变和时变信号的跟踪能力不够[16]。超级电容充放电结束节点前后,由于电流突变为0,RLS方法对参数的修正能力下降,计算结果在工作条件突变时发生较大偏差;在充放电结束阶段和静置阶段,RLS方法能够较准确地模拟超级电容的自放电特性。根据实验结果和仿真结果对比可得,采用RLS方法的综合误差约为2.35%。

图6 双线性变换法仿真结果与实验结果比较
由图6可以看出,双线性变换方法能较好地反映超级电容的动态响应特性。在超级电容充放电结束前后,电流的突变对超级电容的充放电过程影响不大,有效反映了超级电容的充放电动态特性,但是在超级电容静置阶段和自放电阶段,双线性变换方法不能很好地描述其静态特性,模拟计算结果在超级电容静置时偏差较大。根据实验结果和仿真结果对比可得,采用双线性变换方法的综合误差约为2.68%。
对比分析结果表明,RLS法和双线性变换方法均能对超级电容等效电路模型进行参数辨识。针对超级电容不同工步测试条件进行参数辨识时,2种方法有各自不同的优缺点。
4 权值配比优化
根据上述2种方法的参数辨识结果分析,为了保证等效电路模型能准确反映超级电容充放电、自放电特性,即超级电容模型在平稳环境下有良好的自放电特性,在时变环境下有准确的充放电特性。本文综合了2种辨识方法的优点,采用权值配比优化的方法将RLS方法和双线性变换方法的计算机理进行有机结合,对所辨识出的参数值进行加权优化配比,通过控制2种方法在超级电容不同工步阶段的权值对参数辨识结果进行修正。分别设计RLS方法和双线性变换方法的权值为wr和wb,则令
wr+wb=10
(21)
在充放电阶段,令wb>wr;在自放电阶段,令wb 表2 不同权值配比时的工作阶段端电压误差 注:加粗数值指不同工步条件下的端电压误差最小结果。 结合超级电容三分支等效电路模型快慢分支的特点,在权值配比优化的基础上,进一步对模型参数进行分析和修正。在超级电容等效电路模型中,电阻Ri、电容Ci0和可变电容Ci1V组成的快速分支主要完成超级电容的快速充电过程,电容Ci0主要完成超级电容在充满电后的放电工作。因此,对于Ri和Ci0,应选择的权值配比为wr 表3 模型各参数权值配比情况 图7 最优取值配比条件下工作阶段端电压的仿真结果与实验结果 超级电容的自放电和静置指在放电结束后电压出现的下降和自恢复现象[17],主要是由于超级电容在充放电过程中和结束后其内部电荷的重新分配和内部尚未完全停止的电化学反应[18]。为解决这一问题,在充电结束后,给超级电容等效电路模型增加一个微小的电流补偿模拟其电化学反应过程,并结合权值配比优化后的参数修正结果进行验证。为验证权值配比优化方法的有效性和适用性,在超级电容测试平台上,分别在恒流条件下将超级电容充电至额定电压和2.5 V后再进行放电的实验,并采用权值配比优化方法进行参数辨识,将最终的实验结果和模型计算结果进行对比,如图8所示。 (a)超级电容充电至额定电压 (b)超级电容充电至2.5 V图8 多组实验条件下自放电过程优化结果 实验结果和采用权值配比优化方法计算结果的最终误差约为0.9%,因此基于权值配比优化对超级电容等效电路模型参数进行修正,结合超级电容自放电特点对自放电分支进行电流补偿,能准确表征超级电容的实时工作响应特性,验证了所提出的权值配比优化方法对超级电容等效电路模型参数辨识的正确性,提高了超级电容等效电路模型的精度,与RLS法和双线性变换方法相比,辨识精度分别提高了1.45%和1.78%。 采用传统的RLS方法和双线性变换方法辨识超级电容等效电路模型参数时,模型不能完全反映超级电容的动态充放电特性、自放电特性和静态特性。为有效解决上述问题,提高模型精度,本文提出一种基于权值配比优化的超级电容等效电路模型参数辨识方法。在超级电容三分支等效电路模型的基础上,通过可变电容和电压之间的关系拟合可变电容分支的比例参数。分别采用RLS方法和双线性变换方法辨识超级电容等效电路模型各分支的参数,并就2种方法对快速分支、慢速分支与自放电分支的影响进行深入分析,得出权值配比方法在不同工步测试条件下的最优结果。结合RLS方法和双线性变换方法的优点设计了针对超级电容等效电路各分支参数的权值配比优化方法。搭建超级电容等效电路模型,并代入基于权值优化方法计算的参数,将模型计算结果与实验测试结果比较分析。与递推最小二乘法和双线性变换方法相比,采用权值配比优化方法可以更加准确地反映超级电容的充放电特性、自放电特性和静置特性,模型精度分别提高了1.45%和1.78%。 [1] ZHANG Lei, HU Xiaosong, WANG Zhenpo, et al. Experimental impedance investigation of an ultracapacitor at different conditions for electric vehicle applications [J]. Journal of Power Sources, 2015, 287: 129-138. [2] WANG Bin, XU Jun, CAO Binggang, et al. Adaptive mode switch strategy based on simulated annealing optimization of a multi-mode hybrid energy storage system for electric vehicles [J]. Applied Energy, 2017, 194: 596-608. [3] 赵洋, 梁海泉, 张逸成. 电化学超级电容器建模研究现状与展望 [J]. 电工技术学报, 2012, 27(3): 188-195. ZHAO Yang, LIANG Haiquan, ZHANG Yicheng. Review and expectation of modeling research on electrochemical supercapacitor [J]. Transactions of China Electrotechnical Society, 2012, 27(3): 188-195. [4] 王斌, 徐俊, 曹秉刚, 等. 升压型电池-超级电容复合电源的自适应滑模控制 [J]. 西安交通大学学报, 2016, 50(10): 36-41. WANG Bin, XU Jun, CAO Binggang, et al. An adaptive sliding-mode control strategy for hybrid power sources of battery-supercapacitor with a boost converter [J]. Journal of Xi’an Jiaotong University, 2016, 50(10): 36-41. [5] 王斌, 徐俊, 曹秉刚, 等. 一种新型电动汽车复合电源结构及其功率分配策略 [J]. 汽车工程, 2015, 37(9): 1053-1058. WANG Bin, XU Jun, CAO Binggang, et al. A novel hybrid power configuration and its power distribution strategy for electric vehicles [J]. Automotive Engineering, 2015, 37(9): 1053-1058. [6] 梁海泉, 谢维达, 孙家南, 等. 超级电容器时变等效电路模型参数辨识与仿真 [J]. 同济大学学报, 2012, 40(6): 949-954. LIANG Haiquan, XIE Weida, SUN Jianan, et al. Parameter identification and simulation of time-varying equivalent circuit model of supercapacitor [J]. Journal of Tongji University, 2012, 40(6): 949-954. [7] SEDLAKOVA V, SIKULA J, MAJZNER J, et al. Supercapacitor equivalent electrical circuit model based on charges redistribution by diffusion [J]. Journal of Power Sources, 2015, 286: 58-65. [8] 赵洋, 韦莉, 张逸成, 等. 基于粒子群优化的超级电容器模型结构与参数辨识 [J]. 中国电机工程学报, 2012, 32(15): 155-161. ZHAO Yang, WEI Li, ZHANG Yicheng, et al. Structure and parameter identification of supercapacitors based on particle swarm optimization [J]. Proceedings of the CSEE, 2012, 32(15): 155-161. [9] ZHANG Tianping, ZHU Oing, ZHANG Huiyan, et al. Direct adaptive fuzzy control based on integral-type Lyapunov function [J]. Journal of Southeast University, 2003, 19(1): 92-97. [10]GOH C T, CRUDEN A. Bivariate quadratic method in quantifying the differential capacitance and energy capacity of supercapacitors under high current operation [J]. Journal of Power Sources, 2014, 265: 291-298. [11]FARANDA R. A new parameters identification procedure for simplified double layer capacitor two-branch model [J]. Electric Power Systems Research, 2010, 80(4): 363-371. [12]LOGERAIS P O, CAMARA M A, RIOU O, et al. Modeling of a supercapacitor with a multibranch circuit [J]. International Journal of Hydrogen Energy, 2015, 40(39): 13725-13736. [13]DOUGAL R A, GAO L, LIU S. Ultracapacitor model with automatic order selection and capacity scaling for dynamic system simulation [J]. Journal of Power Sources, 2004, 126(1/2): 250-257. [14]DEVILLERS N, JEMEI S, PERA M C, et al. Review of characterization methods for supercapacitor modeling [J]. Journal of Power Sources, 2014, 246: 596-608. [15]索春光, 刘士华, 张文斌, 等. 基于可变电阻的超级电容精确建模方法 [J]. 传感技术学报, 2015, 28(2): 183-187. SUO Chunguang, LIU Shihua, ZHANG Wenbin, et al. Accurate modeling of supercapacitor based on variable resistor [J]. Chinese Journal of Sensors and Actuators, 2015, 28(2): 183-187. [16]陈涵, 刘会金, 李大路, 等. 可变遗忘因子递推最小二乘法对时变参数测 [J]. 高电压技术, 2008, 34(7): 1474-1477. CHEN Han, LIU Huijin, LI Dalu, et al. Time-varying parameters measurement by least square method with variable forgetting factors [J]. High Voltage Engineering, 2008, 34(7): 1474-1477. [17]盖晓东, 杨世彦, 雷磊, 等. 改进的超级电容建模方法及应用 [J]. 北京航空航天大学学报, 2010, 36(2): 172-175. GAI Xiaodong, YANG Shiyan, LEI Lei, et al. Advanced ultracapacitor modeling method and applications [J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(2): 172-175. [18]ZUBIETA L, BONERT R. Characterization of double-layer capacitors for power electronics applications [J]. IEEE Transactions on Industry Applications, 2000, 36(1): 199-205.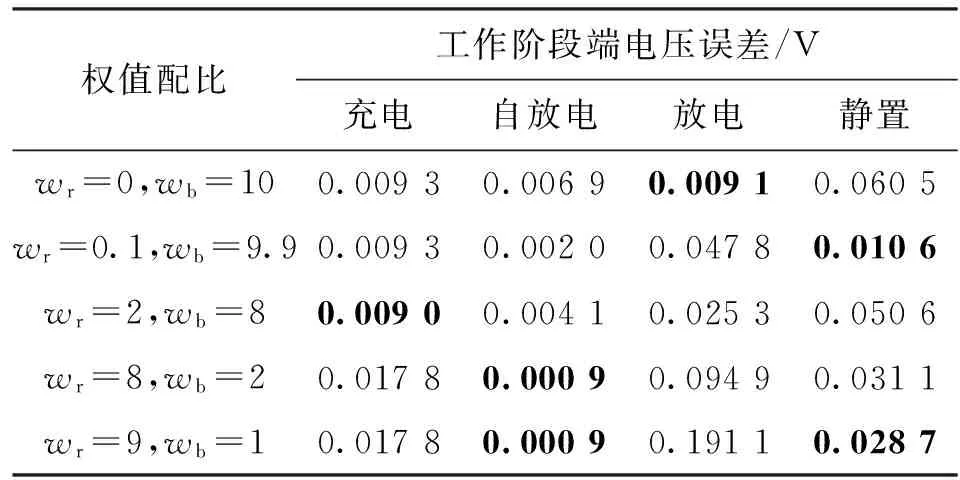




5 结 论

