电热耦合引起的微带传输线无源互调计算与验证
万里鹏,赵小龙,曹智,贺永宁
(西安交通大学微电子学院,710049,西安)
无源互调(Passive Intermodulaton,PIM)是指当多个载波信号通过无源器件时,由于无源器件寄生的非线性特性而产生杂散信号的现象[1]。随着移动通信技术的进步,发射机的功率和接收机的灵敏度不断提高,因无源互调而产生的干扰日益严重,因此无源互调指标已成为衡量通信系统质量的一个重要标准。PCB作为电路元器件的载体,由其所产生的无源互调问题不可忽视[2]。PCB上的无源互调直接地反映在其微带图形上,对基本的微带线进行研究可以直观地分析PIM的来源与变化。
目前,对微带PIM的研究工作大多集中在不同结构微带电路的测试和比较之上,而基于PIM产生机理的物理建模和数学计算研究工作报导较少,对微波部件和电路PIM产物及其规律的量化分析研究相对也不多。因此,本文针对PCB微带线的PIM建模问题,考虑将传输线模型和电热耦合模型相结合,建立了PIM产物对微带线形状参数的计算模型,并研究了PIM产物对微带线结构和频率的依赖关系。为了对微带线结构的PIM信号进行时域量化分析,本文在传统的传输线模型上引入一个电阻非线性系数λ2,将物理空间上分布的非线性源抽象化为数学的非线性系数,计算时在时域将电流表示为各次谐波的叠加,分析三次谐波项的系数,从而建立PIM信号(功率幅值)对与微带线长度的变化关系。为了对微带线上的PIM问题作出物理解释,引入了电热耦合理论[3],电热耦合理论将微带线的非线性解释为分布电阻参数的非线性,由热损耗导致的温变非线性引起[4]。基于电热耦合理论的PIM功率计算考虑了温度、微带线宽度和载波频率等变量,对之前基于传输线的微带线长度与PIM关系做出了补充引入趋肤效应对不同频率下微带线中的PIM功率进行分析。
本文实验验证部分采用多频段PIM测试仪测试了不同频率(700~2 600 MHz)下微带线长度和宽度与PIM功率的关系,该研究结论对于分析PCB印刷线路中无源互调功率的大小具有一定的参考价值。
1 理论计算
1.1 基于电热耦合效应的传输线非线性分析
理想传输线模型将微带线等效为一段均匀的传输线,如图1所示。该模型由4个线性无源元件构成,模型中唯一的变量为传输线长度方向的位移z。

(a)微带传输线等效电路 (b)微带线模型 图1 微带传输线模型
理想的传输线模型完全由线性元器件构成,是一个线性模型。微带线上的非线性来源非常复杂,材料的电导特性、磁滞特性、接触界面状态等一系列因素都会对微带线的PIM产生影响[5],这些因素在数学计算上具有等效性,可以将所有的非线性因素总结为传输线上串联电阻的非线性。在非线性电阻模型中,电阻上的总电压可以表示为线性部分和高次非线性部分的叠加,表达式为
Utotal=I(R0+λ1I+λ2I2+…)=
R0I+λ1I2+λ2I3+…=
U0+Usum2f+Usun3f+…
(1)
式中:R0为常数电阻;λk为k+1阶非线性电阻参量;Usum2f与Usum3f分别为电压中2倍频率组合分量之和与3倍频率组合分量之和。互调问题中主要关心的是总电压中分量中频率为2f1-f2与2f2-f1的项,Usun3f中包含了所需的频率项,故对非线性电阻R作简化,将其表示为以下2个部分[6]
R=R0+λ2(i(z))2
(2)
式中:λ2i(z)2为三阶非线性电阻;λ2为非线性电阻系数,λ2的大小通过实验来进行拟合。为了分析影响非线性强弱的因素,本文结合PIM产生的物理机理,对λ2进行解析计算。覆铜层电热耦合被认为是微带线上PIM产生的主要原因之一,微带线在功率输入下存在导体损耗和介质损耗[7],该损耗以热量的形式耗散,导致局部温度升高。常用金属的电导率是随温度变化的函数,温度升高会导致金属电导率下降,进而改变传输线模型中的电阻阻值,将在原本的常数电阻基础上引入随输入功率(温度)变化的非线性电阻。
电热耦合效应引起的温度的变化是一个复杂的时变过程,为了对问题进行简化,忽略PIM变化对温度变化的响应时间,同时给予足够长的时间让系统达到一个温度平衡的稳定状态,可以将时变问题简化为不含时的稳态问题。在此考虑的电热耦合效应是一个稳态效应,求解的对象是达到平衡状态(即温度不再发生变化)时的互调功率。在温度平衡状态下,电热耦合效应引起的温度变化最终可以归结为由温度变化引起的材料参数的变化,依然是材料非线性问题,此时的互调仍然遵守非线性传输线法则,可以使用非线性传输线方程求解。
根据电热耦合效应,在某一输入功率下,微带线上的温度变化由导体损耗和介质损耗两部分决定。若以ΔPc和ΔPd分别表示单位输入功率下单位长度的传输线导体损耗和介质损耗的功率,其单位功率温度增量为
(3)
式中:Wec和Wed分别为考虑导体损耗和介质损耗两种情况下的等效微带线宽度[8]
(4)
(5)
式中:W为微带线的宽度。
对于输入功率Pin,其温度增量为PinΔT,相应的金属电阻率和电阻为
ρ=ρ0(1+αrPinΔT)
(6)
R=(πfμ0ρP)-1/2
(7)
式中:αr为电阻率-温度系数,铜的αr为0.003 93 Ω·m/K。非线性电阻系数λ2与输入功率的关系由下式决定[9]
(8)
由此式可以看出,λ2与温度、频率和微带线的宽度有关。非线性电阻在此是一个分布参数,可以看成是特定频率和宽度等条件下单位长度微带线贡献的非线性电阻参量。为了分析各参量对微带线PIM功率的影响,用Matlab软件辅助计算,计算过程中默认取微带线长度l=40 cm,微带线宽度W=3.72 mm,频率f=910 MHz,可以得出双载波信号功率为43 dBm时,λ2随微带线宽度、频率的变化的关系如图2所示。
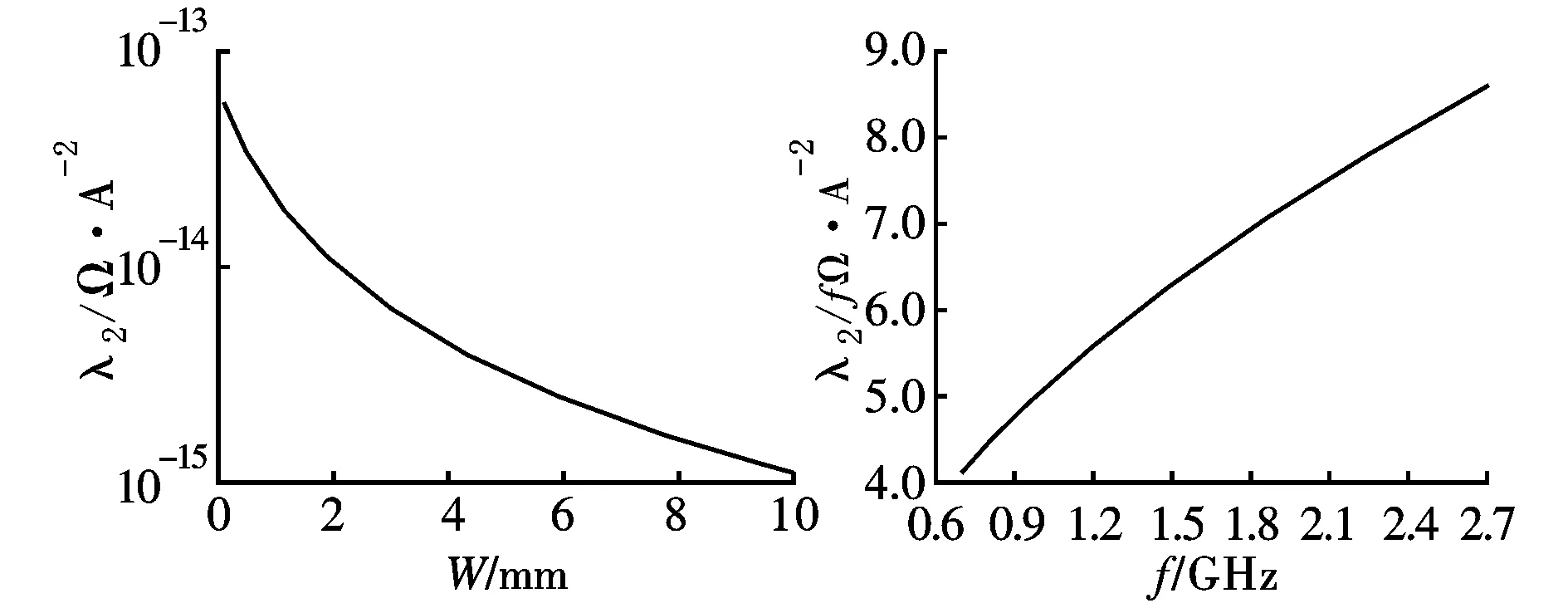
(a)λ2与微带线宽度的关系 (b)λ2与频率的关系图2 λ2与微带线宽度以及频率的关系
根据计算结果,非线性电阻参数λ2预期随着微带线宽度的增加而减小;同时随着互调信号频率的增大,λ2预期呈现增大的趋势。从图2中可以看出,微带线宽度和互调信号频率对λ2的影响较小。
将λ2代入微带线模型,由戴维宁和诺顿等效原理可得微带传输线方程如下
(9)
将该方程组联立后可得
(10)
式中:A2=(R0+jωL)(G+jωC);B=R2(G+jωC)。
方程(9)是一个二阶非线性齐次方程,描述了传输线中总体电流的分布状态。为了计算传输线中的3阶PIM功率,在此只需得到3次谐波电流分量的解,常用的处理方法是将总电流i(z)表示为不同谐波项与傅里叶级数之积的叠加[10],考虑等式两边电流谐波项的阶数相等,代入电流的级数表达式
(11)
式中:a+d+g=p;b+e+h=q;c+f+i=k-1。
为了得到频率为(2f1-f2)的3阶互调信号的大小,令k=1,p=2,q=1,分离出3次谐波所在项。当k=1时,方程(10)解的形式为
Nq,p,1e-Aq,p(l-z)+Lq,p,1(z)
(12)
在式(12)等式右边,前两部分之和为方程的通解,Lq,p,1(z)为方程的特解[11]。Aq,p=[(R0+jωq,pL)(G+jωq,p/C)]-1/2,其中ωq,p=2π(pf1+qf2)。根据边界条件可以得到系数M与N的表达式,最终3阶PIM功率由下式计算得到
(13)

使用Matlab软件进行辅助计算,两路载波功率皆取43 dBm,计算过程中默认取微带线长度l=40 cm,微带线宽度W=3.72 mm,频率f=910 MHz,最终可以得到3阶PIM功率随长度方向z的变化关系,代入λ2随微带线宽度的关系,同时可以得到3阶PIM功率随微带线宽度的变化关系,如图3所示。
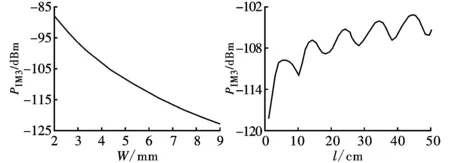
(a)微带线宽度的影响 (b)微带线长度的影响图3 微带线长度与宽度对3阶PIM功率的影响
从图3可以看出,随着微带线长度的增加,PIM功率预期呈现波动增大的趋势。随着微带线宽度的增大,单位宽度的微带线流过的电流密度减小,结合图2中得到的微带线宽度与非线性电阻系数λ2的变化关系可知,相比于λ2,传输线中电流密度大小对微带线宽度的变化更为敏感,是决定不同宽度的微带线中PIM功率的主要因素。
1.2 趋肤效应下载波频率与PIM功率的关系
λ2随频率的变化关系已经解得,为了求解不同频率下的PIM功率,还需求解不同频率下微带线中的电流密度变化。根据趋肤效应,电流在导体中的分布随频率的升高而逐渐减小。如图1b所示,忽略边缘效应,由于电磁波在导体中存在传播损耗,微带线中的电流集中在x>0处的一小部分区域内,因此微带线中z方向上的面电流密度随着进入上导体中的深度的增加而不断衰减,其相对关系为
Js(x)=Js0e-γx
(14)
式中:Js0为微带线上导体的表面(x=0)电流密度;γ为电磁波在上导体中的传播系数,是一个复数量。由于其虚部不会引入电磁波的幅值衰减,为了简化计算,只考虑引起衰减的实部。
设上导体的非线性电阻率为ρ2,在z方向上取单位长度,则ρ2=SR2,由R2引起的PIM功率可以表示为
(15)
令ΔS→0,得到非线性电流功率

(16)
由式(2)可以得到R2与λ2的关系为R2=λ2i(z)2,将其代入式(16),考虑3阶反射(z=0)互调产物,由此可得PIM功率与频率的关系为

(17)
式中,λ2与频率的关系由图2b给出,λ2具体的表达式非常复杂,在此借助计算机软件直接计算给出λ2与频率之间的相对关系。取两路载波信号功率为43 dBm、微带线长度l=40 cm、微带线宽度W=3.72 mm时,PIM功率随频率变化的曲线如图4所示。
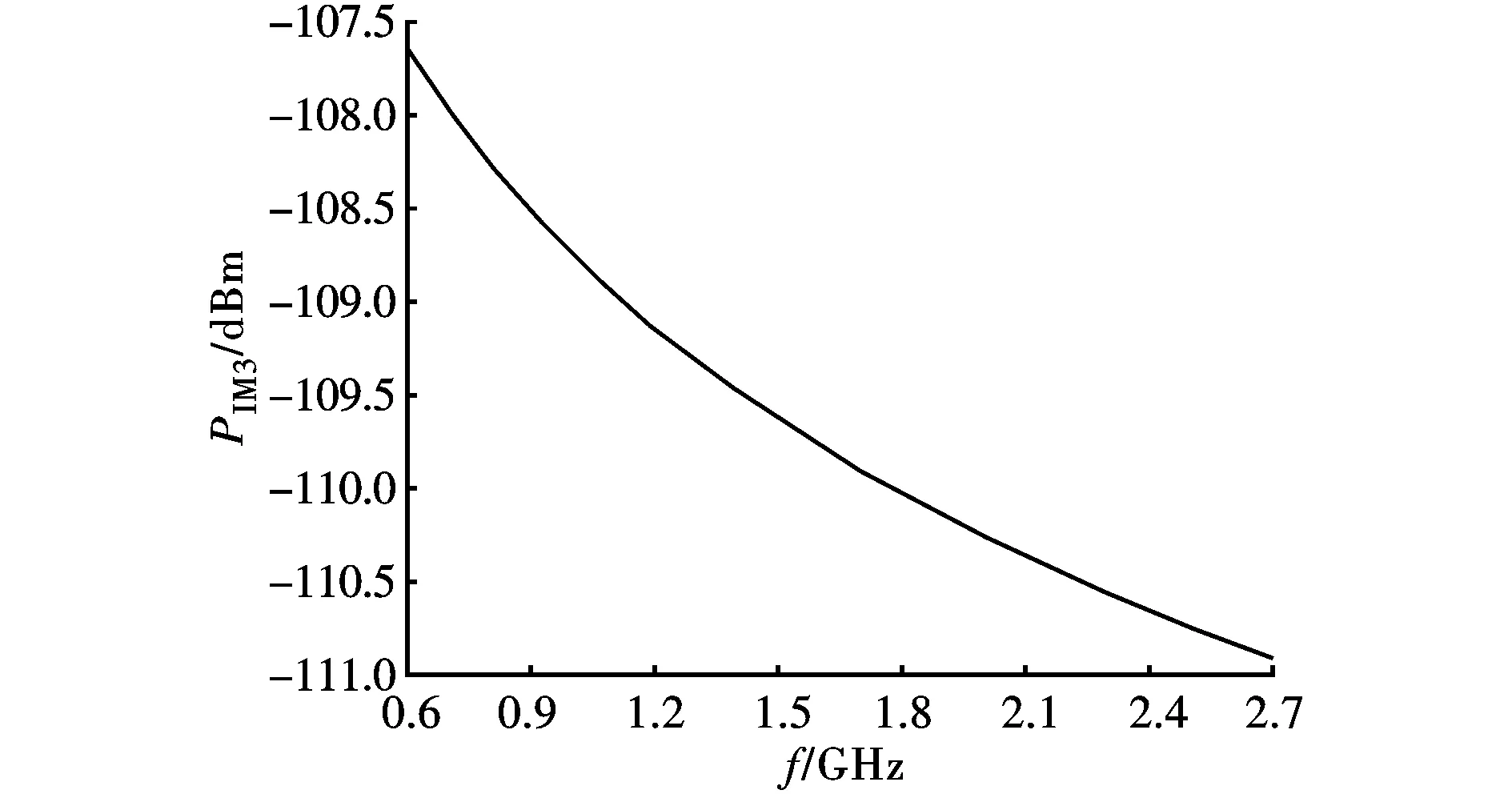
图4 微带线中3阶PIM功率随频率的变化关系
从图4可以看出,预期PIM功率随着互调信号频率的升高而下降。
2 实验验证与分析
为了对计算结果进行验证,测试了一系列不同长度和宽度的微带线的PIM特性。测试使用的微带线由泰州博泰公司提供,介质板厚度为1 mm,介质的相对介电常数为2.5,铜箔厚度为0.035 μm。微带线PIM的测试方法包括有线传输反射和探针近场耦合[12]两种,这里采用传统的有线反射PIM测试法。取两路功率为20W,采用频率f1、f2相近的双音信号对待测微带线进行激励,在微带线的另一端连接一个低互调负载,用双工器取反射信号进行分析,观测其中3阶互调(2f1-f2)信号的功率。测试系统的结构[13]如图5所示。
实验1,选取长度从5~46 cm的50 Ω微带线进行测试;实验2,选取宽度从2~9 mm,长度为40 cm的微带线进行测试;实验3,选取不同的宽度的微带线,在700~2 600 MHz频率范围内进行测试。测试过程中用到的双音信号功率为2×40 dBm,得出3阶PIM功率与微带线长度、宽度、频率的变化关系如图6所示。
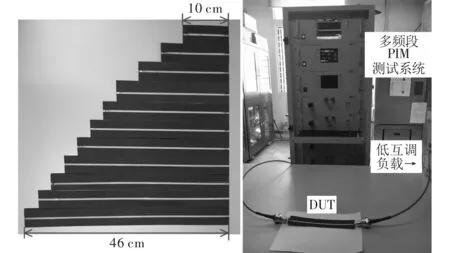
(a)微带线测试样本 (b)微带线PIM测试现场
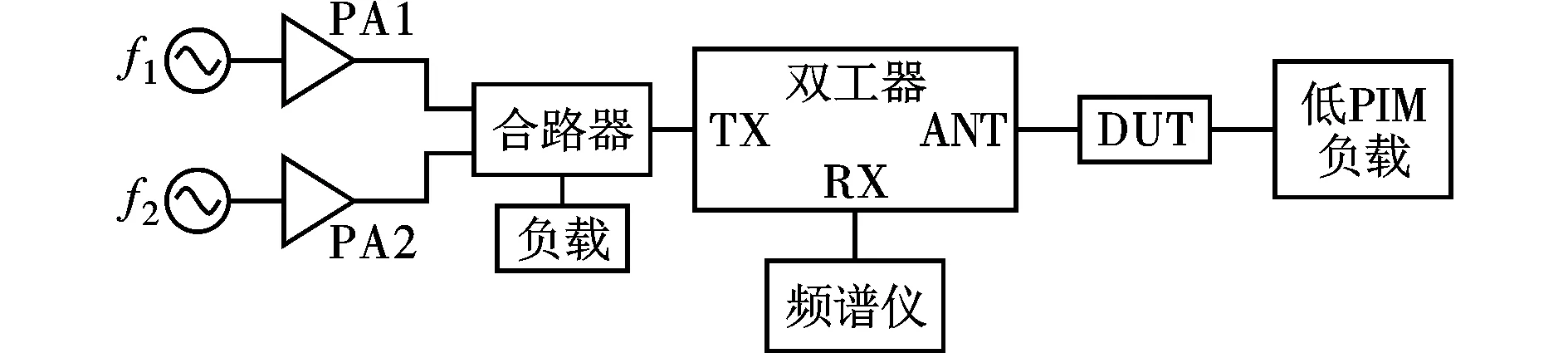
(c)测试系统的结构框图图5 微带线PIM功率测试方案
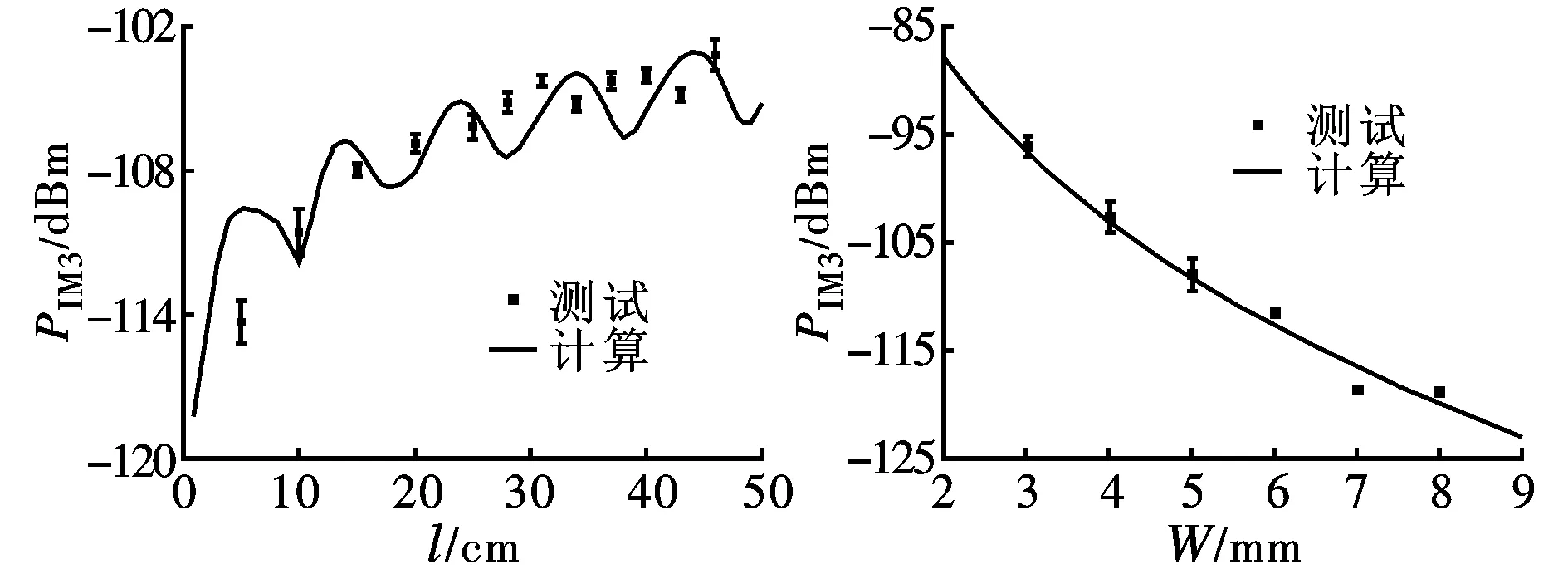
(a)PIM功率-微带线长度关系 (b)PIM功率-微带线宽度关系

(c)PIM功率-频率关系图6 3阶PIM功率与不同变量关系的计算与测试结果
所用测试系统的底噪功率约为-135 dBm,从测试结果可以看出,由于制造工艺引入的表面粗糙、材料非线性等非理想效应,该批微带线所能测得的最低PIM功率约为-120 dBm。
由图6a可知,随着微带线长度的增加,PIM功率呈现出波动增大的趋势,且其增幅不断下降,与计算结果吻合。这是因为非线性系数λ2是单位长度微带线分布的非线性电阻效应,随着微带线长度的增加,微带线上的分布非线性源随之增多,贡献的总体非线性功率呈现增大的趋势。与此同时,PIM测试采用的是反射PIM测试法,由于不同线源与测量点之间距离不同。不同线源产生的PIM谐波相位不同,相位随距离的波动最终表现为PIM功率随长度的波动,由此可以观察到一个随长度波动的PIM功率。由于微带线是有损的,随着距离的增加,较远非线性线源产生的PIM谐波在传输到测试点时会产生衰减,距离越长,衰减越严重。这就导致随着微带线长度的增大,由非线性线源贡献的PIM功率呈现减小的趋势。这在测试结果中得到了体现,随着微带线长度的增加,PIM的增幅不断减小。
由图6b可知,随着微带线宽度的增大,PIM功率不断减小。微带线上的非线性由电流激励非线性源引起,非线性强弱以及电流密度都是影响PIM功率的因素。随着微带线宽度增大,非线性线源λ2增大,同时微带线上导体的电流密度变小。不考虑其他因素的影响,λ2与微带线宽度的关系是正相关的,而电流密度与微带线宽度的关系是负相关的,后者的负相关关系起到了主导作用,这一点在实验中也得到了验证。
在图6c中,随着测试频率的增加,PIM功率不断减小,这一点与计算结果一致。频率对PIM功率的影响表现在两个方面:非线性系数λ2随着频率的增加而增大,同时总电流密度由于趋肤效应随频率的增大而不断减小。后者对PIM功率的影响起主要作用,最终导致PIM功率随频率的增大而减小。
3 结 论
本文将电热耦合效应应用到了非线性传输线模型上,提出了一种微带结构的无源互调计算的方法,并通过实验对计算结果进行了验证。通过计算推导得出,随着微带线长度的增加,PIM功率波动增大,且增幅减小。在此基础上考虑趋肤效应与电流密度的变化,可得随着微带线宽度和频率的增大,PIM功率都呈现出下降的趋势。该研究结论对于PCB上的PIM量化分析与预测具有参考价值。
[1] 叶鸣, 肖怡, 陶长英, 等. 微带传输线的无源互调效应实验研究 [J]. 电波科学学报, 2014, 29(3): 471-475. YE Ming, XIAO Yi, TAO Changying, et al. Experimental research on passive intermodulation effect of microstrip lines [J]. Chinese Journal of Radio Science, 2014, 29(3): 471-475.
[2] SHITVOV A P, ZELENCHUK D E, SCHUCHINSKY A G, et al. Passive intermodulation in printed lines: effects of trace dimensions and substrate [J]. IET Microwaves Antennas and Propagation, 2009, 3(2): 260-268.
[3] WILKERSON J R, GARD K G, STEER M B. Electro-thermal passive intermodulation distortion in microwave attenuators [C]∥Proceedings of the 36th European Microwave Conference, Piscataway, NJ, USA: IEEE, 2006: 157-160.
[4] ROCAS E, COLLADO C, ORLOFF N D, et al. Passive intermodulation due to self-heating in printed transmission lines [J]. IEEE Transactions on Microwave Theory & Techniques, 2011, 59(2): 311-322.
[5] SHITVOV A P, ZELENCHUK D E, SCHUCHINSKY A G, et al. Passive intermodulation generation on printed lines: near-field probing and observations [J]. IEEE Transactions on Microwave Theory and Techniques, 2008, 56(12): 3121-3128.
[6] ZELENCHUK D E, SHITVOV A P, SCHUCHINSKY A G, et al. Passive Intermodulation in finite lengths of printed microstrip lines [J]. IEEE Transactions on Microwave Theory and Techniques, 2008, 56(11): 2426-2434.
[7] POZAR D M. Microwave engineering [M]. 3rd ed. Hoboken, NJ, USA: John Wiley & Sons, 2011: 124-125.
[8] BAHL I J, GUPTA K C. Average power-handling capability of microstrip lines [J]. IEE Journal on Microwaves, Optics and Acoustics, 1979, 3(1): 1-4.
[9] 叶鸣, 贺永宁, 崔万照. 基于电热耦合效应的微带线无源互调机理研究 [J]. 电波科学学报, 2013, 28(2): 18-23. YE Ming, HE Yongning, CUI Wanzhao. Passive intermodulation mechanism of microstrip lines based on the electro-thermal coupling effect [J]. Chinese Journal of Radio Science, 2013, 28(2): 18-23.
[10]JIANG J H, ZHANG S Q, WU S Z, et al. Prediction of passive intermodulation power level based on double exponential function model and genetic algorithm [C]∥Proceedings of 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference. Piscataway, NJ, USA: IEEE, 2011: 307-310.
[11]ZELENCHUK D, SHITVOV A P, SCHUCHINSKY A G, et al. Passive intermodulation on microstrip lines [C]∥Proceedings of the 37 the European Microwave Conference. Piscataway, NJ, USA: IEEE, 2007: 396-399.
[12]HIENONEN S, RAISANEN A V. Passive intermodulation near-field measurements on microstrip lines [C]∥Proceeding of the 34th European Microwave Conference. Piscataway, NJ, USA: IEEE, 2004: 1041-1044.
[13]林鑫海, 邹勇, 谢树民, 等. 多系统合路POI无源互调测量研究 [J]. 移动通信, 2016, 40(2): 32-36. LIN Xinhai, ZOU Yong, XIE Shumin, et al. Research on passive intermodulation measurement of POI [J]. Mobile Communications, 2016, 40(2): 32-36.

