基于点云投影的瓷砖凸包特征点检测

赵 谦，任志奇

(西安科技大学 通信与信息工程学院，陕西 西安 710054)

0 引 言

随着国家经济的飞速发展，市场对瓷砖质量提出了严苛的标准。由于瓷砖生产工艺特殊，批量生产时质量难以保证的特点，因此对瓷砖进行无损平整度检测具有重大意义。目前绝大多数企业的瓷砖平整度检测主要依靠人工，存在检测效率低，工作强度大，质量不稳定，漏检率高等问题[1]。

近几年3D扫描技术的发展日益成熟，这为瓷砖检测带来了新的技术手段[2]。目前瓷砖平整度检测设备主要采用激光位移传感器[3-5]来获取瓷砖特征点信息，也有一些采用容栅位移传感器[6]、光纤位移传感器[7]、PSD传感器[8]等等。这些设备检测精度高、速度快，但造价昂贵、装置复杂、维护成本高。而3D扫描仪体积轻便、装置简单、扫描精度高，可在极短时间内快速获取物面三维点云，将其用于瓷砖平整度检测是可行的。由于瓷砖点云离散无序，瓷砖平整度检测所需的特征点位置未知。为此本文提出一种基于点云投影的瓷砖凸包特征点检测算法，可从瓷砖点云中自动快速提取瓷砖特征点坐标。

1 系统简介

实验所采用的3D扫描系统为光轴交叉型光路结构，如图1所示，P为结构光场的投影系统(Projector)，成像系统(Camera)为接受变形光栅像的面阵探测器，本系统采用CCD(Charge-Coupled Device，电荷耦合元件)摄像机。投影系统的光轴PO和成像系统的光轴CO相交于参考平面(Reference Plane)上的O点，参考平面与成像系统的光轴垂直。光栅像被投影系统投影到待测物体表面，A和B是参考平面上的点，H是物面的被测点，由于受到物体高度分布h(x, y)的空间调制，观察系统将得到携带有物体高度分布信息的变形光栅像。L是成像系统出瞳到参考平面的距离，d是成像系统与投影系统之间的距离。

系统由信息采集模块和计算模块组成，如图2所示。信息采集模块主要由投影仪(Projector)向待测物体表面投射三频彩色光栅(Three-Frequency Color Grating)，用彩色CCD获取彩色条纹变形图，作为算法模块的输入。算法模块则通过条纹变形图解调出条纹图的相位信息，进一步重建出扫描对象的三维信息。系统采用彩色条纹投影与立体视觉融合的三维传感方法，以测量复杂动态物体(Dynamic Object)。其基础原理是一种双向融合机制，即先用三频彩色条纹的相位分布指导双目立体视觉全局匹配，反过来，再利用双目条纹灰度图局部多特征的精细匹配校正初始相位失真，这种失真来源于反射率噪声、形状突变以及条纹的非正弦性，最终用立体视觉求解空间点位置坐标。

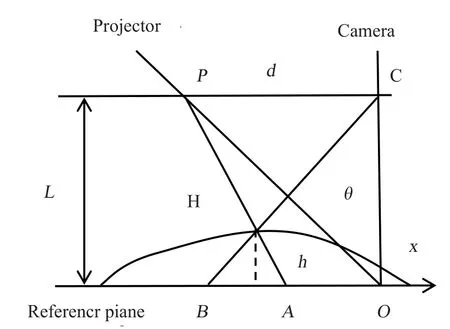
图1 3D扫描系统光路原理图Fig.1 Optical path schematic of 3D scanning system

2 算法描述

2.1 瓷砖平整度

中华人民共和国国家标准《GB/T 3810.2-2016》(《瓷砖试验方法 第2部分：尺寸和表面质量的检验》)对瓷砖平整度的定义如下。

中心弯曲度：砖面的中心点偏离由4个角点中的3点所确定的平面的距离[9]。

边弯曲度：砖一条边的中点偏离由4个角点中的3点所确定的平面的距离[9]。

翘曲度：由砖的3个角点确定一个平面，第4角点偏离该平面的距离[9]。

实际应用中，边弯曲度的计算与国家标准略有不同。通常做法是取瓷砖一边上的3个四等分点(也称边特征点)，分别计算这3个点到任意3个角点所确定平面的距离，然后取最大值作为该边的边弯曲度。可见瓷砖平整度检测的关键是获取瓷砖平面的3类特征点坐标：4个角点、12个边特征点、1个中心点。

2.2 凸包算法

瓷砖特征点中最重要的是对瓷砖4个角点的检测，为此引入计算几何中的凸包模型来对角点进行描述。凸集是理解凸包的前提，凸集的定义如下：假设在平面上有非空点集S，在S中任取两点p1，p2，如果点p=tp1+ (1-t)p2∈S，其中，0≤t≤1，则称是S凸集。换言之，如果S中任意两点所连线段全部位于S之中，那么S就是凸集，显然，带有“凹部”的任何平面点集都不是凸集。在凸集的基础上，凸包定义为包含平面点集S的最小凸集，关于凸包可以这样想象：在地面上固定若干木桩，用根绳子将这些木桩尽量紧地圈起来，所形成的凸多边形就是凸包。图3和图4展示了瓷砖点云的三维凸包模型以及点云投影的二维凸包模型，这两个模型是后面两个瓷砖特征点检测算法的基础。

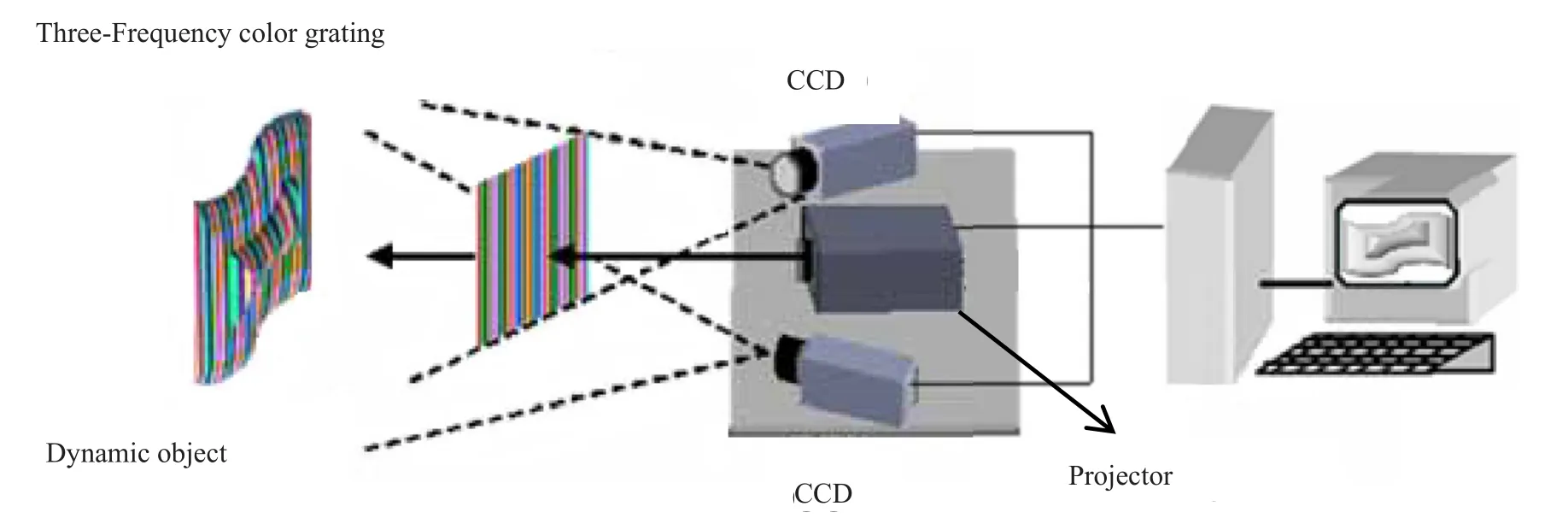
图2 彩色条纹投影与双目立体视觉融合3D扫描系统Fig.2 3D scanning system with color fringe projection and binocular stereo vision fusion

目前求解凸包的算法有卷包裹法、Graham方法以及分治算法等等，而Graham方法是求解平面点集凸包问题的最佳算法[10]，故重点介绍Graham方法，其步骤如下：

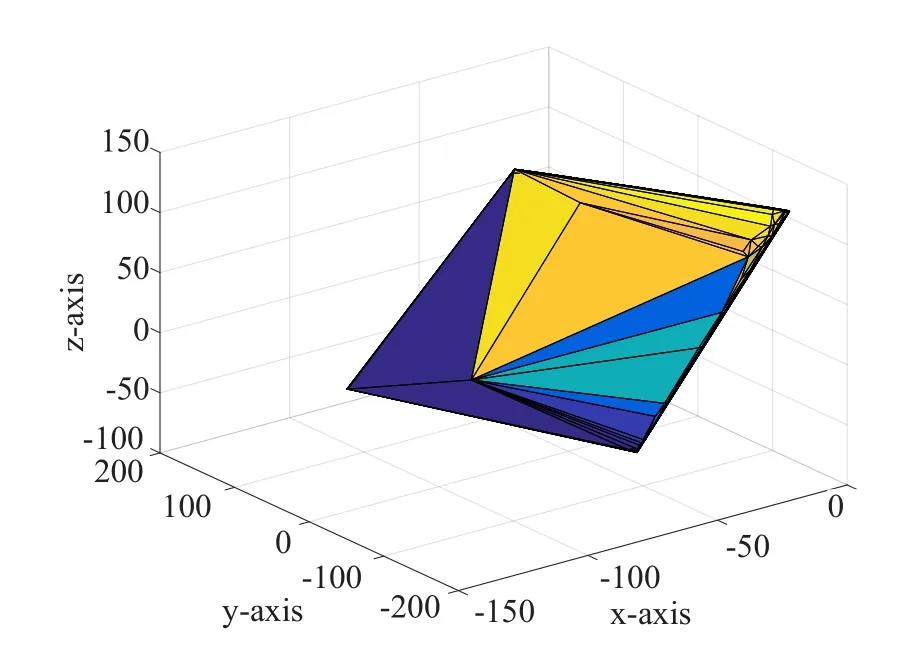
图3 瓷砖点云三维凸包Fig.3 Tile point cloud three-dimensional convex hul

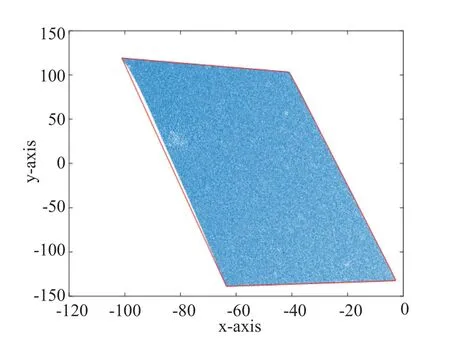
图4 瓷砖点云投影凸包Fig.4 Tile point cloud projection convex hull

(1)设凸集中y坐标最小的点为p1，如果有多个y坐标最小点，则以x坐标最小的点为p1。将p1与凸集中其它各点用线段连接，然后计算各线段与水平线的夹角，并按夹角大小以及到p1的距离进行词典式分类，得到序列p1, p2, p3, …, pn，用线段依次连接这些点，得到一个多边形。p1是凸包边界的起点，p2与pn也必是凸包顶点。pn+1=pn，如图5所示。

(a)根据各点倾角大小以及到p1的距离进行词典式分类

(b)以p1为起点，逆时针连线成一多边形

(d)原p4成为p3，p1和p4在同侧，p3暂时在边界上，继续查下去

(e)最后得到凸包的6个顶点

(2)删去p3, p4, …, pn-1, 中不是凸包顶点的点，方法如下：

步骤1：k←4；

步骤2：j←2；

步骤3：如果p1和pk分别在两侧，则删去pk-1，后继顶点编号减1，k←k- 1，j←j- 1；否则pk-1暂为凸包顶点，并记录；

步骤4：j←j + 1，转至步骤3，直至j←k-1；

步骤5：k←k + 1，转至步骤2，直至k←n + 1。

(3)顺序输出凸包顶点。

2.3 瓷砖特征点检测算法

假设瓷砖表面点云为P(x, y, z)，Pxy(x, y)为点云投影，瓷砖点云数为n。令角点D4={d1, d2, d3, d4}，边特征点B4={d1i, d2i, d3i, d4i}, (i=1, 2, 3)，中心点0xy。令角点投影D4xy={d1xy, d2xy, d3xy, d4xy}，边特征点投影B4xy={b1ixy, b2ixy, b3ixy, b4ixy},(i=1, 2, 3)，中心点投影Oxy。根据作用域的不同，瓷砖特征点检测可分为直接检测与间接检测两种。前者直接在三维点云中寻找特征点坐标，后者先将三维点云映射至二维平面，在该平面检测特征点投影，最后将特征点投影反映射至三维点云空间，即可得到瓷砖真实的特征点坐标。

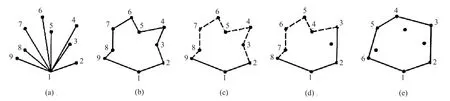
图5 Graham方法的解释Fig.5 Interpretation of the Graham method

2.3.1 算法1：直接检测算法

第一步：角点估计

获取P(x,y,z)的凸包，记凸包顶点集合为T(x,y,z)；

计算T(x,y,z)内各点之间的距离，距离最大的两个点记为角点d1、d3；

过d1、d3构造直线L13，满足L13(x, y, z) ≥ 0的部分记为T1(x, y, z)，满足L13(x, y, z)＜0的部分记为T2(x, y, z)；

计算T1(x, y, z)内各点到直线L13的距离，距离最大的点为角点d2；

计算T2(x, y, z)内各点到直线L13的距离，距离最大的点为角点d4。

第二步：边特征点估计

以角点d1、d2所在边的四等分点b1i,(i=1, 2, 3)为例，假设第一步所求d1、d2的坐标分别为d1(x1, y1, z1)和d2(x2, y2, z2)，则b1i坐标计算过程如下：

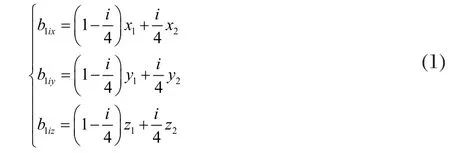
其中，i=1, 2, 3，表示3个四等分点；

若b1i在P(x, y, z)中，则b1i为所求的四等分点，否则以距b1i最近的点为四等分点b1i(注意：本段及论文后面的“距某点最近的点”可由K最近邻(K-Nearest Neighbor，KNN)算法实现，KNN是机器学习的基本算法)；

同理可得其它三组四等分点b2i、b3i、b4i。第三步：中心点估计记O'(xavg , yavg , zavg)，

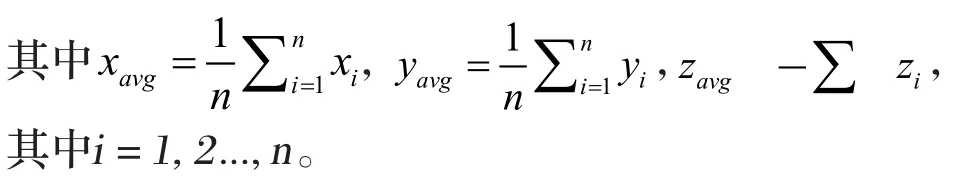
若O'在P(x, y, z)中，则O'为中心点O，否则以距O'最近的点为中心点O。

2.3.2 算法2：点云投影检测算法第一步：角点投影估计

获取Pxy(x, y)的凸包，记凸包顶点集合为T(x, y)；

计算T(x, y)内各点之间的距离，距离最大的两个点记为角点投影d1xy、d3xy；

过d1xy、d2xy构造直线L13，满足L13(x, y, z) ≥ 0的部分记为T1(x, y)，满足L13(x, y, z)＜0的部分记为T2(x, y)；

计算T1(x, y)内各点到直线L13的距离，距离最大的点为角点投影d2xy；

计算T2(x, y)内各点到直线L13的距离，距离最大的点为角点投影d4xy；

第二步：边四等分点投影估计

以角点投影d1xy、d2xy所在边的四等分点投影b1ixy,(i=1, 2, 3)为例，假设第一步所求d1xy、d2xy的坐标分别为d1xy(x1xy,y1xy)和d2xy(x2xy,y2xy)，则b1ixy坐标计算如下：

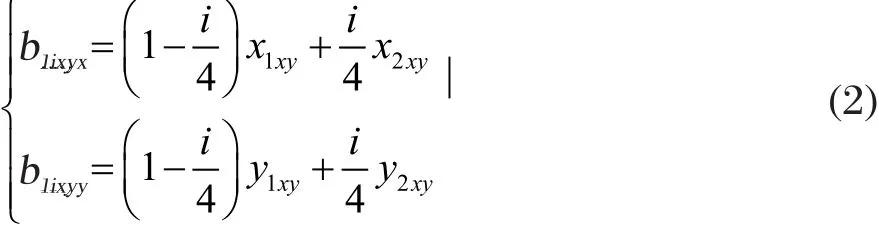
其中i=1, 2, 3，表示3个四等分点投影；

若b1ixy在Pxy(x, y)中，则b1ixy为所求的四等分点投影，否则以距b1ixy最近的点为四等分点投影b1ixy；

同理可得其它三组四等分点投影b2ixy、b3ixy、b4ixy。第三步：中心点投影估计

记O'(xavg ,yavg ,zavg )，其中

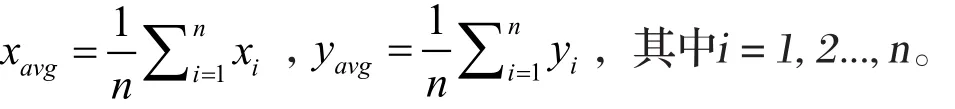
若O'在Pxy(x, y)中，则O'xy为中心点投影Oxy，否则以距O'xy最近的点为中心点投影Oxy。第四步：点云投影特征点映射

根据P(x, y, z)到Pxy(x, y)的映射关系，将上述特征点投影进行3D映射，即：

3 算法仿真

3.1 实验环境(见表1)

表1 实验环境Tab.1 Experimental environment

3.2 仿真结果与分析

3D扫描系统对图6所示的白色光面瓷砖(300*300 mm)进行扫描，获得瓷砖表面密集点云，点云数达100000，为强化视觉效果，对该点云进行抽样，使其点云数降至10000，作为后面显示瓷砖特征点的背景点云。分别见图7、图8。

用算法1和算法2分别提取瓷砖特征点，提取效果如图9、图10所示，特征点坐标数据如表2、表3所示。

图6 白色光面瓷砖Fig.6 White glossy tiles

观察表2和表3，发现算法1与算法2分别获取的特征点坐标有细微差异，这是因为算法1和算法2的作用空间不同，前者是在三维空间(空间点云)，后者是在二维空间(点云投影)。根据空间点及其投影关系易知，三维空间距离最大的两个点，在二维平面上的投影距离未必最大(可以想象这样一个场景，在桌面上竖立一支铅笔，笔头和笔尾距离最长，但笔头与笔尾的投影在笔尾处重合，其投影点的距离为零)，所以算法1所得凸包中的d1、d3和算法2凸包中的d1xy、d3xy不一定满足fpxy→p映射关系，其余特征点情况类似。由前面铅笔的例子可以发现，如果点云数据本身存在干扰点(在z轴方向上距离点云平面偏大的点)，算法1有可能会得到错误的结果，而算法2则不然，其点云投影以及反映射的处理过程使其可以排除Z轴方向上的干扰点，这也表明算法2的抗干扰性要强于算法1。

为形象比较算法1和算法2所得瓷砖特征点坐标的差异，下面给出两组坐标在x、y、z三个坐标轴上的差异图及其相关图(相关图上的点越逼近直线，证明其相关程度或相似度越高)。需要说明的是，由于两组坐标过于相似，为增强显示效果，在显示算法2所得坐标时，统一将其下移3个单位，显示效果如下。

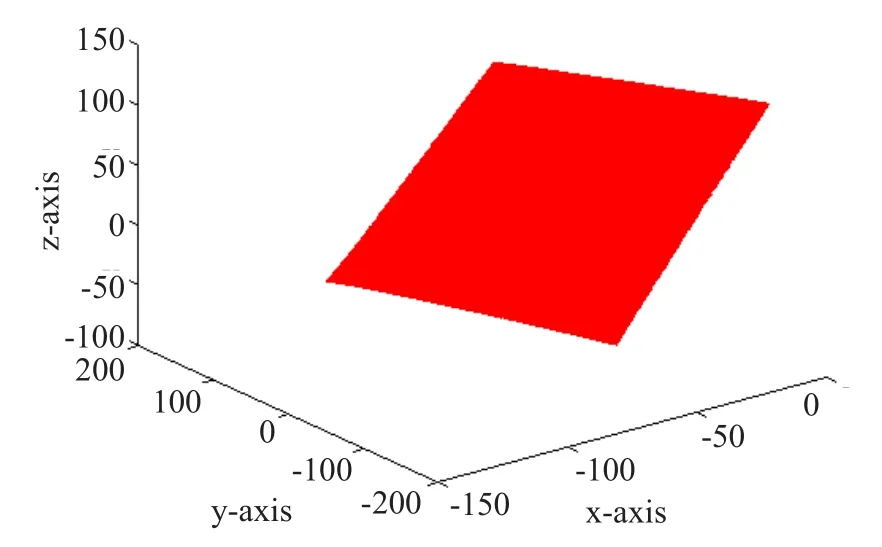
图7 瓷砖表面点云(点云数：100000)Fig.7 Tile surface point cloud (Point cloud number: 100000)

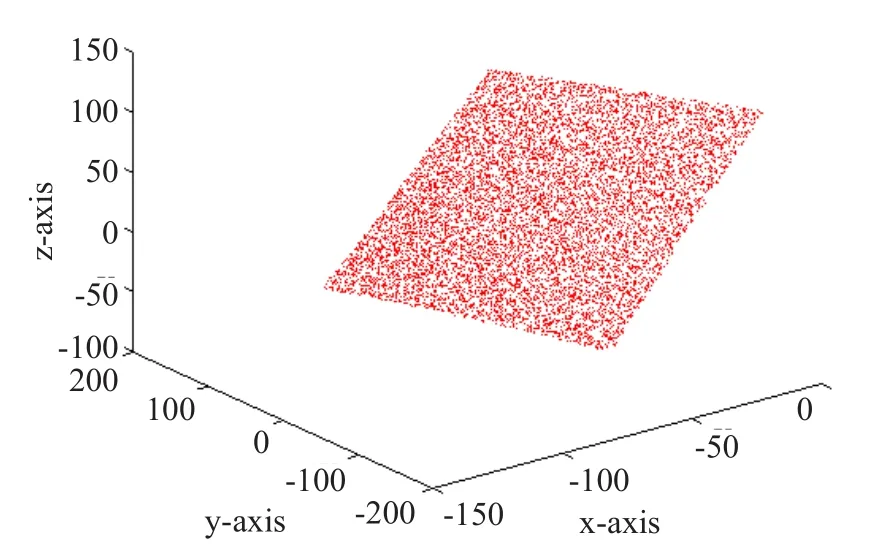
图8 瓷砖表面点云(点云数：10000)Fig.8 Tile surface point cloud (Point cloud number: 10000)

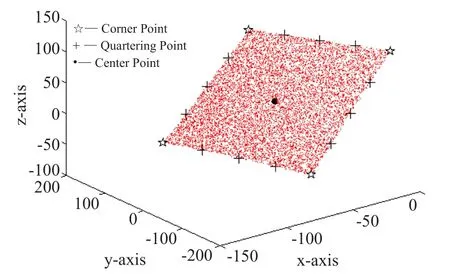
图9 算法1所得瓷砖特征点Fig.9 Tile feature points resulting from Algorithm 1

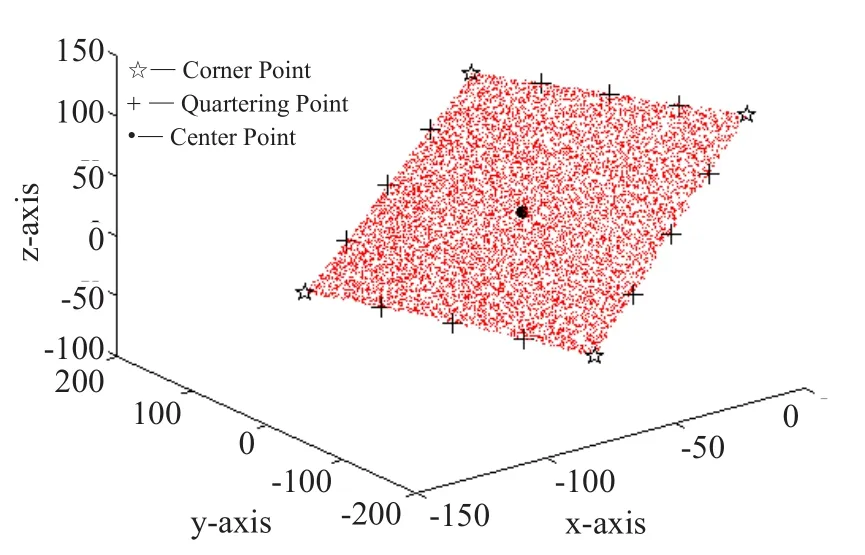
图10 算法2所得瓷砖特征点Fig.10 Tile feature points resulting from Algorithm 2

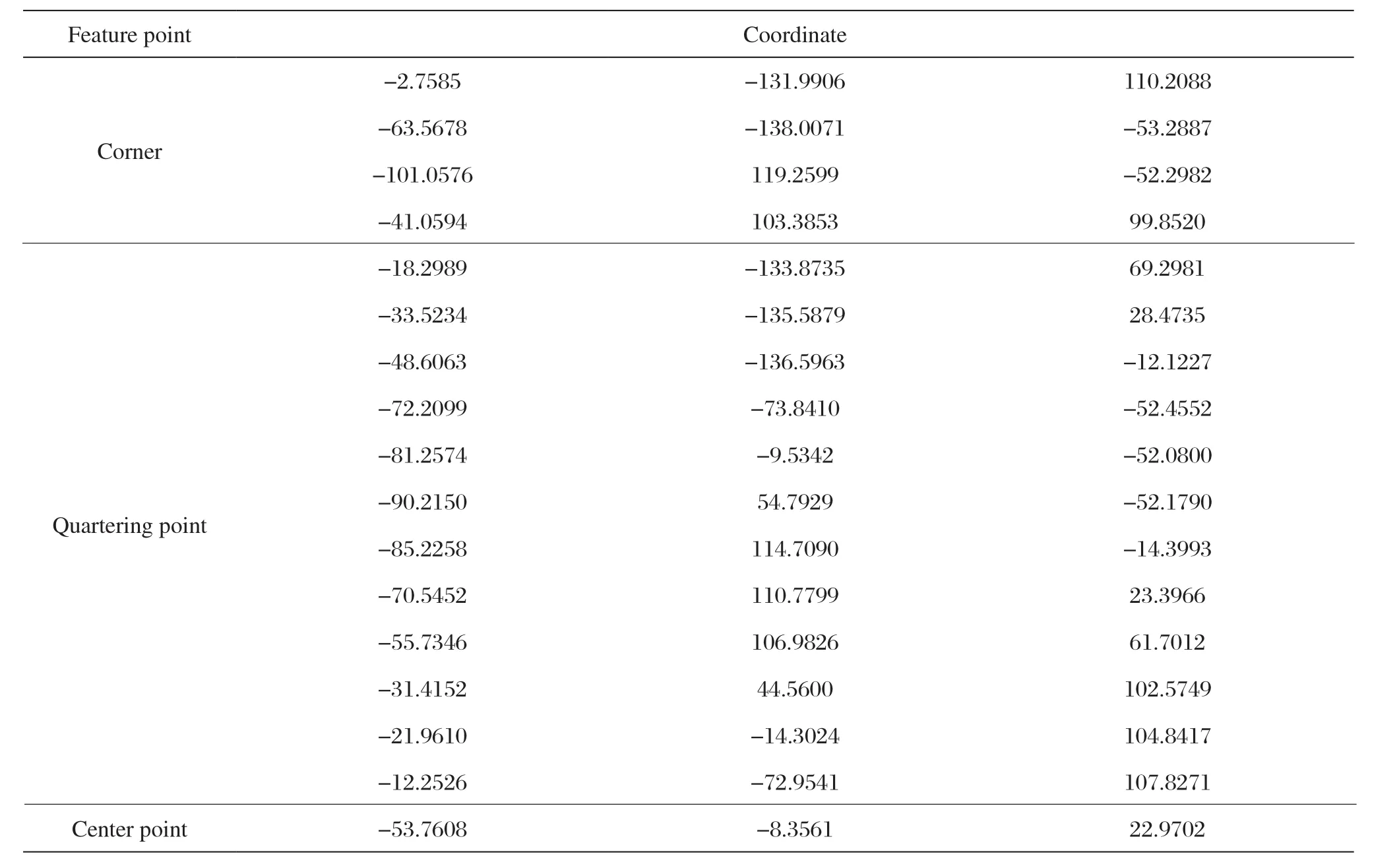
表2 算法1检测的瓷砖特征点坐标Tab.2 Tile feature point coordinates detected by Algorithm 1

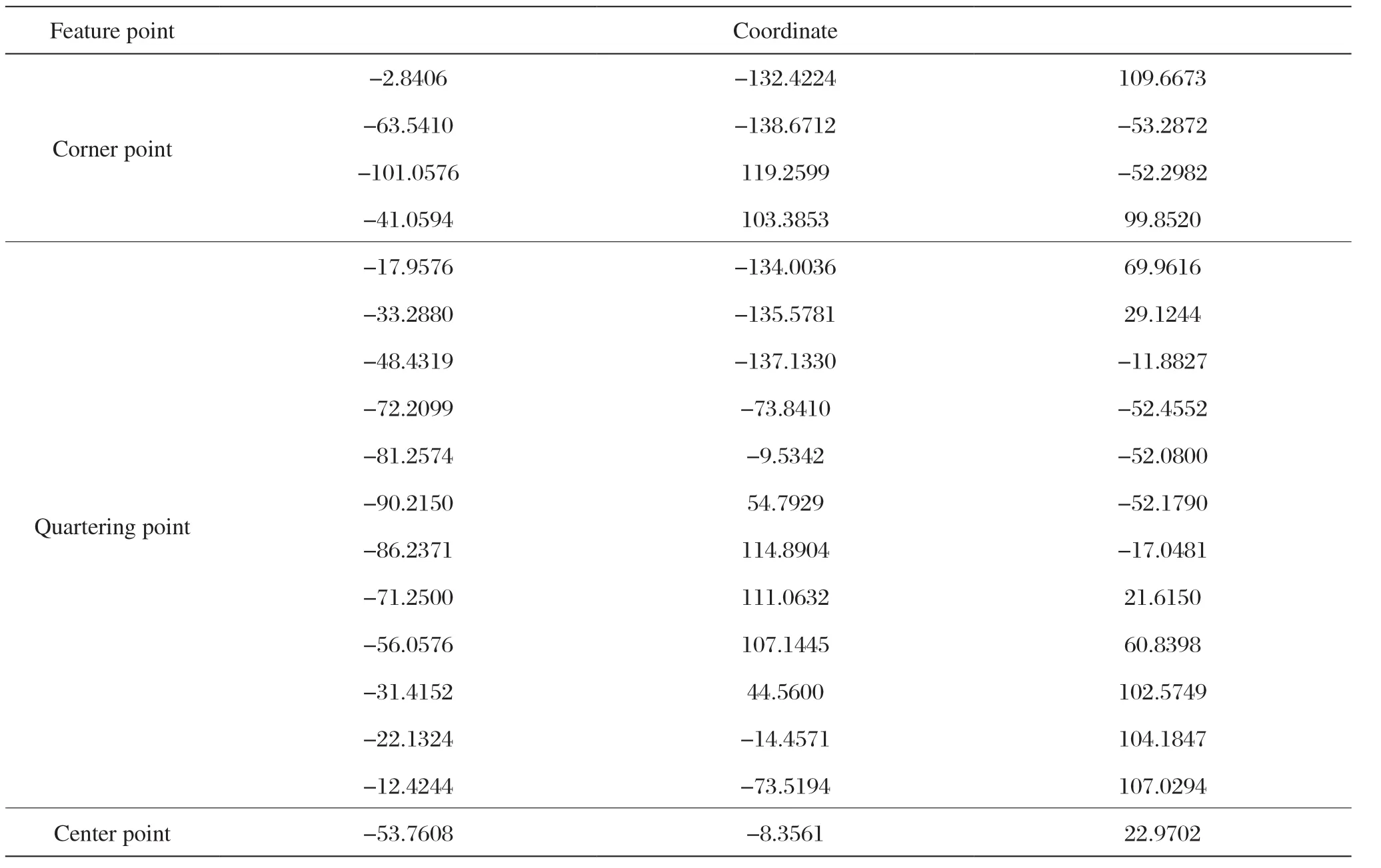
表3 算法2检测的瓷砖特征点坐标Tab.3 Tile feature point coordinates detected by Algorithm 2

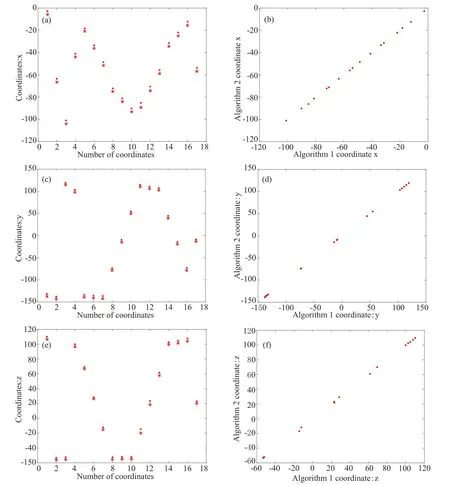
图11 算法1、算法2所得瓷砖特征点坐标示意图及相关图(图(a)(b)(e)标记点说明：‘.’算法1特征点坐标；‘＊’算法2特征点坐标)Figure.11 Schematic diagrams for detection of tile feature point coordinates by Algorithm 1 and algorithm 2(Marking points in (a)(b)(e): ‘.’ Algorithm 1 detected feature point coordinates; ‘*’ Algorithm 2 detected feature point coordinates)

由于本实验3D扫描系统的高精度性能，算法1与算法2所得瓷砖特征点坐标误差极小。从瓷砖特征点坐标相关图(图11(b)、(d)、(f))可以看到，两组特征点坐标的x、y、z坐标相关图呈线性分布，证明两组坐标相关度极高。用MATLAB自带的corr2()函数比较两组坐标数据的相似度，其x坐标相似度为0.9999，y坐标相似度为1.0000，z坐标相似度为0.9999，总体相似度为1.0000，验证了我们的判断。

下面比较算法1与算法2的执行效率，分别统计二者各运行10次的时间，如表4所示。

由上表可以看到算法2比算法1的运行效率更高。这是由于算法1直接在三维空间中寻找凸包，而瓷砖点云不一定全部处于同一平面，此时多个凸包顶点存在交叉，而算法2不存在这个问题。理论上二维空间点集的凸包顶点数满足三维空间点集的凸包定点数满足n为100000时二者比值为6.81。本实验中算法1所得三维凸包顶点数高达360，去掉重复点为119，算法2为20，二者比值为5.95，与理论值6.81相比这个数值是合理的。很容易理解，凸包顶点数越多算法的运行时间也就越长，在这里近似认为算法运行时间与凸包定点数呈正相关，由于算法2有一个从二维到三维的反映射过程，因此算法2与算法1的运行时间比值要小于5.95，而实际比值为3.28，故算法2的运行效率是算法1的3倍以上是合理的。

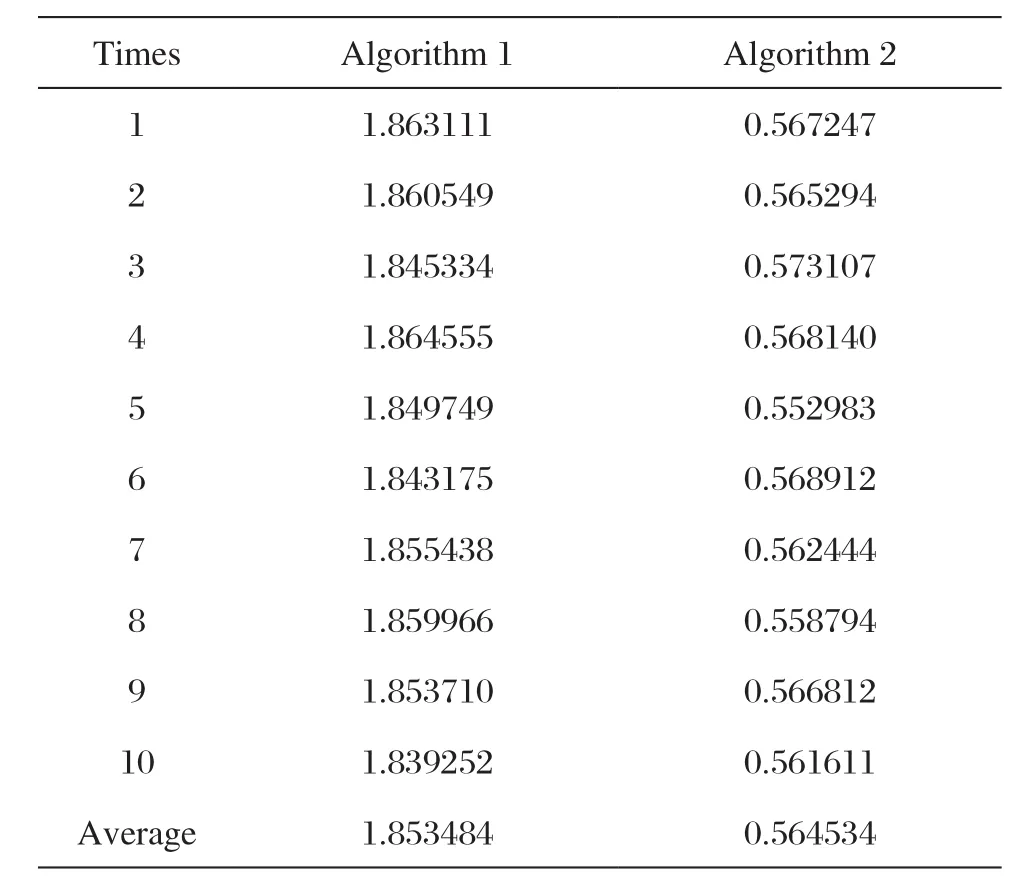
表4 算法执行时间(单位：秒)Tab.4 Algorithm running time (Unit: second)

4 结 论

本文将3D扫描技术用于瓷砖平整度检测领域，并提出了一种基于点云投影的瓷砖凸包特征点检测算法。算法创造性地将三维空间中特征点的检测转换为在二维空间中对其特征点投影的检测，极大提高了算法执行效率。实验证明，本文提出的点云投影检测算法性能明显优于直接检测算法，不仅具备一定的抗噪能力，而且执行效率较高，0.6秒内便可完成瓷砖特征点的提取，这对3D扫描仪应用于瓷砖平整度检测实现自动化、高效化具有重要意义。