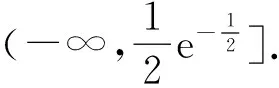细节决定成败
——以2017年浙江高考数学卷中的易错点为例
浙江临海市回浦中学
李昌湛 (邮编:317000)
2017年浙江省首次新高考在广大一线老师和社会各界的密切关注下落下帷幕.今年的数学试卷保持了浙江卷一贯以来的简洁、朴实、明了的特点,试题看似熟悉平淡,但将数学思想方法和核心素养作为考查的重点,淡化了特殊的技巧,全面考查通性通法,体现了以知识为载体,以方法为依托,以能力考查为目的的命题要求,凸显了试题的层次和品位.据阅卷老师反馈,虽然试卷看似简单,但是我们的学生还是出现了会而不对、对而不全的现象.本文分析试卷中的易错点及备考建议,希望对读者有所帮助.
1 数学概念不清导致的错误
例1(2017年浙江卷12)已知a、b∈R,(a+bi)2=3+4i(i是虚数单位),则a2+b2=______,ab=______.
分析本题重点考查复数的概念和基本运算,由复数的乘法运算得(a+bi)2=(a2-b2)+2abi,而有的学生错误地写成(a+bi)2=(a2+b2)+2abi,导致做错.这里出错的原因是复数的基本概念及运算不熟悉,尤其要注意i2=-1.正确答案是5和2.
例2(2017年浙江卷16)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有______种不同的选法.(用数字作答)

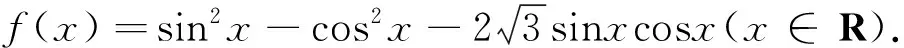
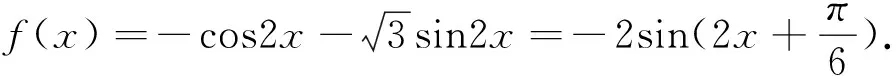
备考建议准确理解数学概念是解题的前提.解答这类问题理解题意很关键,一定要多读题才能挖掘出隐含条件,所以复习时不能忽视或淡化对数学概念的复习.新的数学《考试说明》也指出:要求对所学知识内容有理性认识,知道知识间的逻辑关系.能用数学语言对相关问题进行描述,对比较、判断、讨论的过程作出恰当的表述.具备利用所学知识解决简单问题的能力.
2 运算与数据处理能力薄弱导致的错误
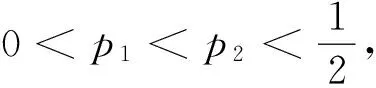
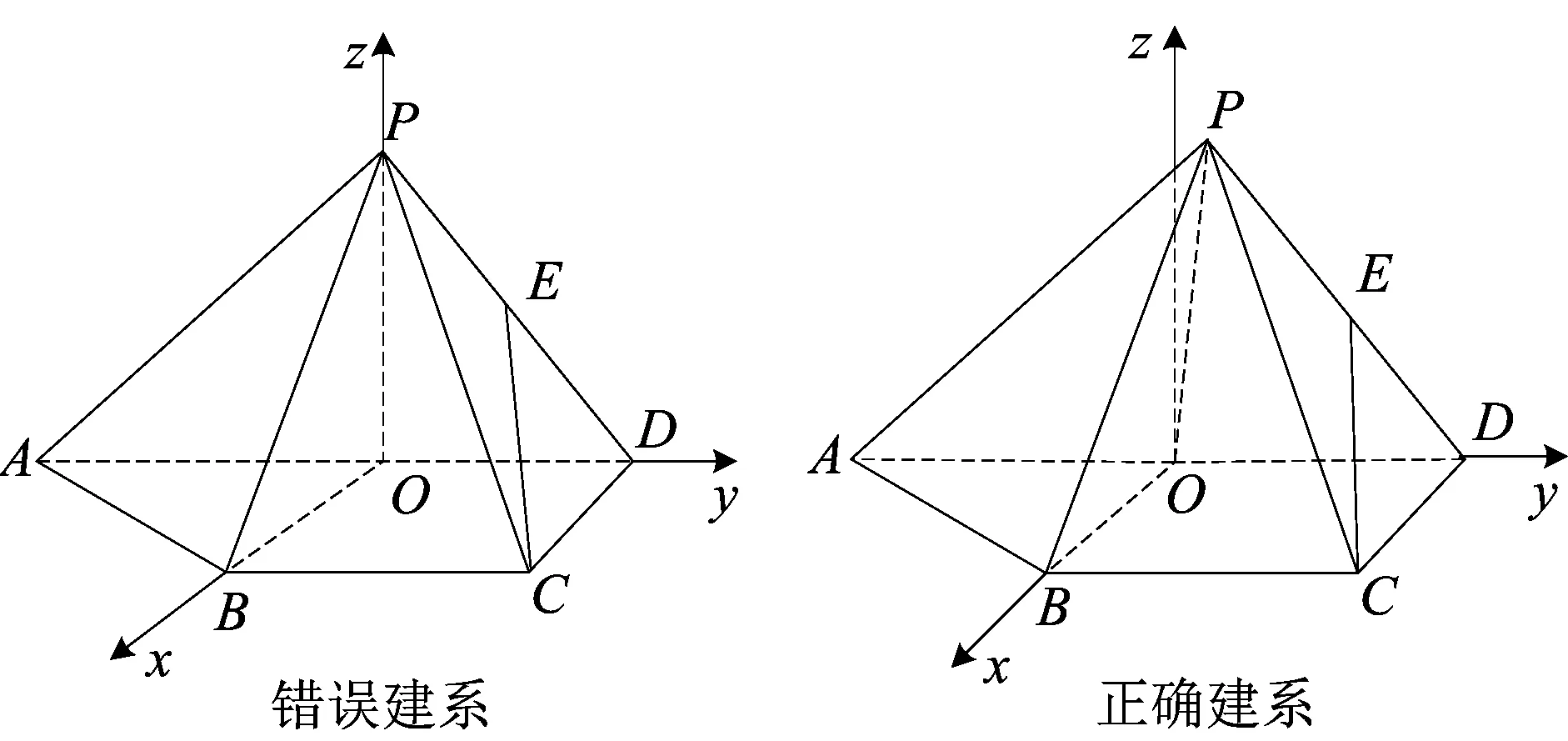
A.E(ξ1) B.E(ξ1) C.E(ξ1)>E(ξ2),D(ξ1) D.E(ξ1)>E(ξ2),D(ξ1)>D(ξ2) 分析本题符号多,再如果运算能力差,有的学生就容易出错,解决办法把已知数据画成分布列问题就清楚、简单多了: ξ101ξ201P1-p1p1P1-p2p2 从而,E(ξ1)=p1,E(ξ2)=p2,则E(ξ1) 当然,如果学生能看出这是两点分布,并知道两点分布的期望与方差公式,那么本题的计算量还是不大的. 分析这是第20题的第(Ⅰ)小题,学生考后说没想到本大题的第(Ⅰ)小题只求函数的导数,问题看似简单平淡,但从阅卷的反馈情况来看,很多学生第(Ⅰ)小题就做错了,导致第(Ⅱ)小题也没有完成.这暴露了大部分学生运算与数据处理能力的薄弱,终因小问题酿成大损失,甚是可惜.利用求导法则和求导公式,可得如下正确的求解过程: 备考建议现在的学生运算能力普遍比较薄弱,一道题目算算最后就不知道哪里算错了,计算出错是导致学生失分的“头号杀手”.在平时的复习课中,老师要有意识加强计算能力的培养.新的数学《考试说明》也指出:运算求解能力是指能根据法则、公式进行正确运算、变形的能力;根据问题的条件和目标,寻找多种途径,并能比较不同途径的特点,设计较为适合的方法进行运算、变形的能力;根据要求进行估计和近似计算的能力. 例6(2017年浙江卷19)如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点,求直线CE与平面PBC所成角的正弦值. 列表: x12(12,1)1(1,52)52(52,+∞)f'(x)-0+0-f(x)12e-12↘0↗12e-52↘ 备考建议图象有时会欺骗人的眼睛,不能想当然,只有通过正确的计算与推理才能得出正确的结论.新的数学《考试说明》也指出:能正确分析几何体的位置关系与数量关系,并对几何体的位置关系和数量关系进行论证与求解. 纵观2017年的浙江卷,学生最容易在数学概念、运算能力、图形图象上失分,这些问题看似细枝末节,但严重影响学生得分的高低,俗话说:细节决定成败.希望能引起我们老师的足够重视.


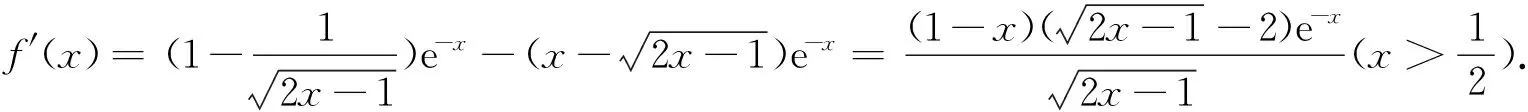
3 图象画错导致的错误