一类条件为abc=1型不等式的证法探究
安徽省岳西县汤池中学
苏岳祥 杨续亮 (邮编:246620)
在《数学通讯》(上半月刊)的问题征解,《中等数学》数学奥林匹克问题,《数学教学》问题与解答以及各级数学竞赛试题中,经常出现abc=1条件的三元不等式证明试题,笔者对含有“abc=1”的条件不等式的证明进行了深入的探究,总结出五种证明不等式的方法.
1 运用公式直接证明
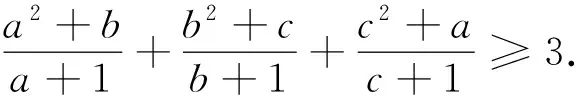
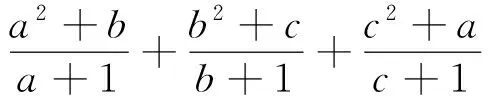
=3.
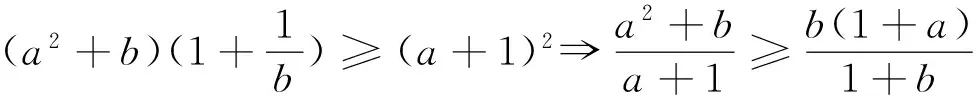
例2(2015年摩尔多瓦数学奥林匹克试题)已知a、b、c是满足abc=1的正实数,
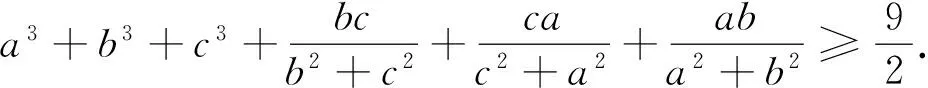
证明因为(a+b)(a-b)2+(b+c)(b-c)2+(c+a)(c-a)2≥0,
所以2(a3+b3+c3)≥a(b2+c2)+b(c2+a2)+c(a2+b2)≥6.因此
评注证明时对不等式进行了分拆,局部运用均值不等式或者柯西不等式.
2 常数“1”的代换
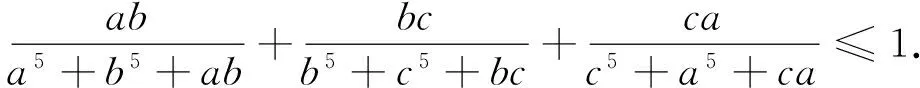
证明注意到a5+b5-a2b2(a+b)=(a2-b2)(a3-b3)≥0.
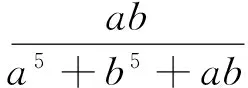
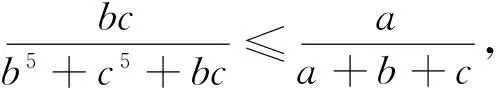
评注利用1=abc代换时,考虑到代数式的齐次式特征,实现有效的等价代换.
3 结构化换元
3.1 倒数换元
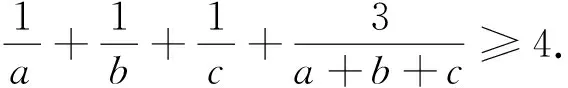
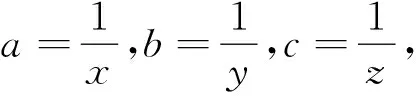
由于(x+y+z)2=x2+y2+z2+2(yz+zx+xy)≥3(yz+zx+xy),
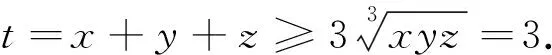
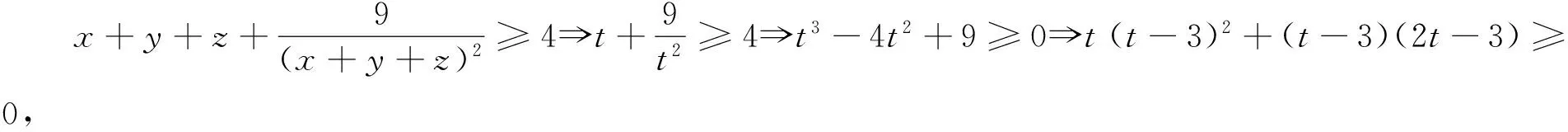
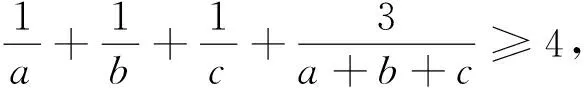
例5(2008年全国高中数学联赛山东省预赛试题)设实数x>0,y>0,z>0,且xyz=1.
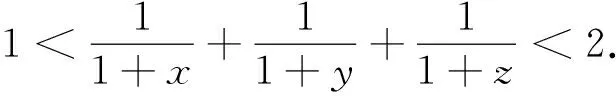
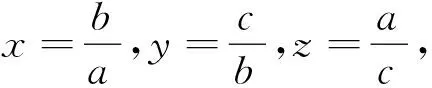
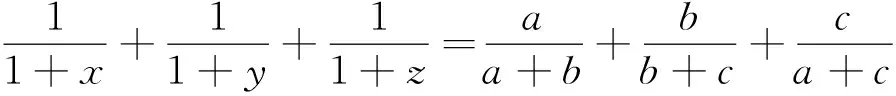
故不等式得证.
无独有偶,在2016年辽宁省竞赛也有这样一道试题:

评注这种代换可以解决第41解IMO试题.
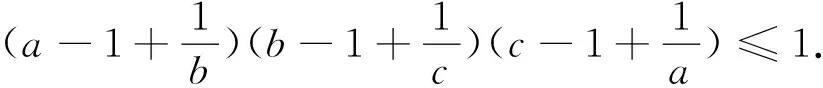
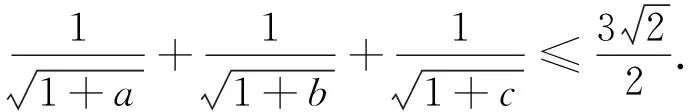
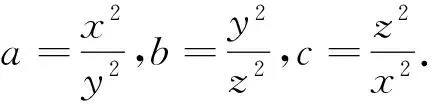

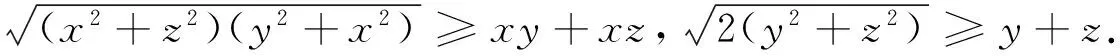
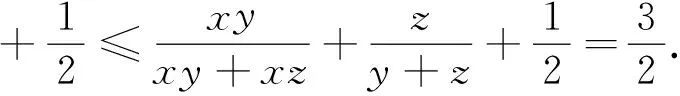
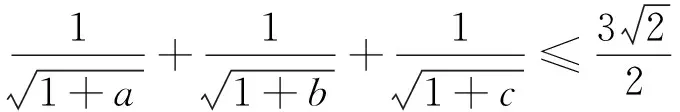
评注换元以后得到了第四届中国西部数学奥林匹克第8题 求证: 对任意的正实数a、b、c都有

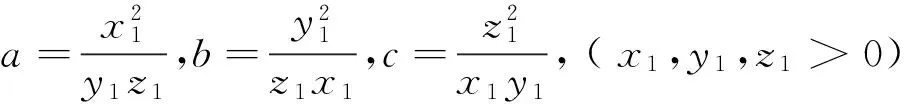
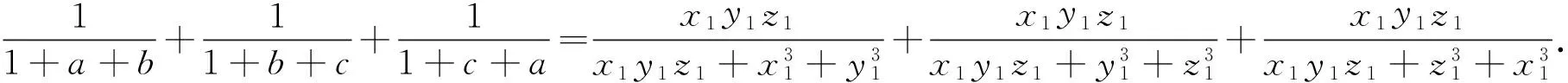
故
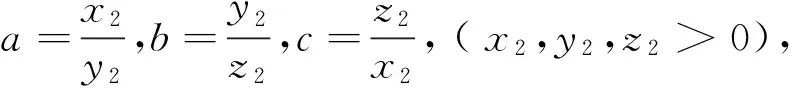
由柯西不等式可得
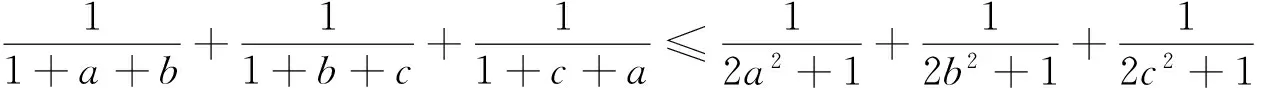
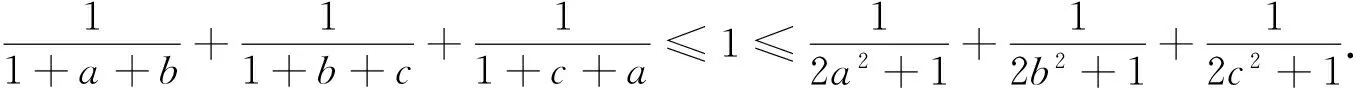
3.5 a=x3,b=y3,c=z3换元
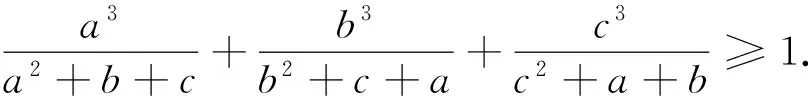
证明令a=x3,b=y3,c=z3(x,y,z>0),
由(y4-z4)(y-z)≥0得y5+z5≥y4z+z4y=yz(y3+z3),

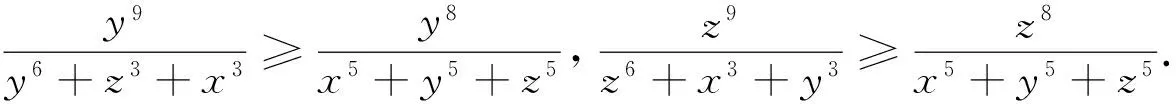
又有6x8+y8+z8≥8x6yz=8x5,x8+6y8+z8≥8xy6z=8y5,x8+y8+6z8≥8xyz6=8z5,
以上三式相加可得
x8+y8+z8≥x5+y5+z5.
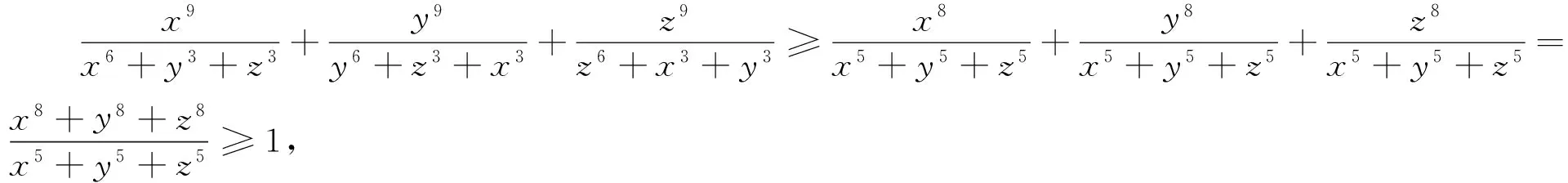
4 其它变换
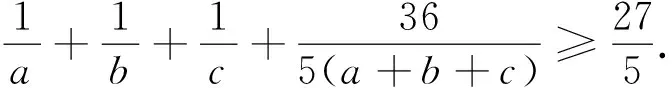

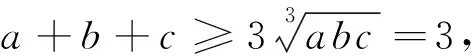

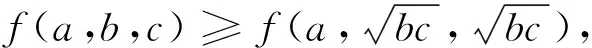
因此要证原不等式成立,只需要证明

故所证不等式变为
整理可得
10x6-54x4+61x3-27x+10≥0,
而当0 10x6-54x4+61x3-27x+10 =(x-1)2(10x4+20x3-24x2-7x+10) ≥0, 从而原不等式成立. 即a+b+c-1=ab+bc+ca,故 =a2+b2+c2 =(a+b+c)2-2(ab+bc+ca) =(a+b+c)2-2(a+b+c-1) =(a+b+c-1)2≥1,得证. 又由均值不等式可得 以上三式相加可得. 评注例11实质上是波罗的海数学竞赛试题的题源. 设a、b、c为正实数,且abc=1,求证 化简可得.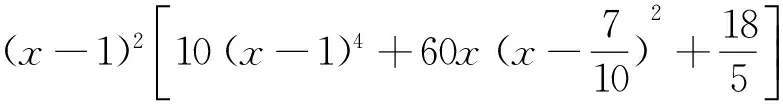
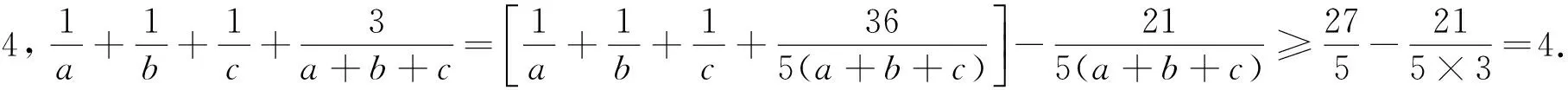
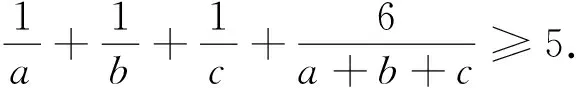
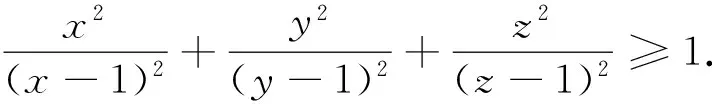


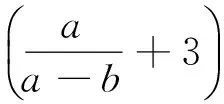
5 待定系数法