基于PSO-BP神经网络的摩托车排放预测

王志红，贺星驰1,，吴鹏辉1,，袁 雨1,

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070；2.武汉理工大学 汽车零部件技术湖北省协同创新中心，湖北 武汉 430070)

近年来我国汽车保有量快速增加，机动车的尾气排放已经成为城市空气污染的主要来源。截止至2017年，摩托车保有量已经达到了8 244.0万辆[1]，占中国机动车保有量的29.91%。2016年中国机动车排放的CO、NOx和HC这3项污染物的总量为4 419.1万吨[2]，其中摩托车排放的CO、HC和NOx总量为404.8万吨、54.3万吨和9.1万吨，分别占比12.0%、12.9%以及1.6%，控制摩托车的排放已经成为摩托车行业发展的战略任务。2016年中国发布的摩托车污染物排放限值及测量方法(中国第四阶段)(GB 14622-2016)[3]和轻便摩托车污染物排放限值及测量方法(中国第四阶段)(GB 18176-2016)[4]从2018年7月1日正式实行，其对于摩托车的排放提出了更为严格的要求。

国内外学者针对尾气排放预测进行了大量研究并且提出了多种进行排放预测的方法。周斌[5]提出了不使用传统的数学建模而是引进BP神经网络进行排放性能预测的设想，并通过具体实施对其进行了验证。文华[6]开发了一种预测柴油机NOx瞬态排放的方法，该方法加入遗传优化算法防止BP(back propagation)神经网络出现“过拟合”，结果表明使用该方法的预测精度较高。Taghavifar[7]采用CFD(computational fluid dynamic)与人工神经网络结合的方法，对内燃机排放的CO2、NOx和烟度进行了预测，预测结果与实测数据线性高度相关。

笔者以某正三轮摩托车为研究对象，在底盘测功机上对其进行了排气污染物排放测试。依据测试结果，以BP神经网络为基础，并引入粒子群算法优化神经网络，建立了基于PSO-BP(particle swarm optimization-back propagation)神经网络的摩托车排放预测模型。

1 排放试验

1.1 试验用主要设备

在排气污染物排放试验中，主要设备包括底盘测功机、取样设备以及分析设备等。底盘测功机是摩托车排气污染物排放试验中的主要试验平台，它能够模拟摩托车在实际道路行驶的工况。取样设备与摩托车排气管连接，对摩托车排气进行采集。分析设备对取样气体进行分析得出摩托车的排放数据。具体试验设备参数如表1所示。

1.2 试验车辆与试验方案

以某正三轮摩托车作为测试车辆，测试车辆的主要参数如表2所示。

试验由6个市区试验工况循环组成，正三轮摩托车在排气污染物排放试验中的行驶工况如图1所示。

表1 试验设备参数

表2 测试车辆参数

图1 试验工况循环图

2 PSO-BP神经网络排放预测模型2.1 数据准备与预处理

初始测量数据量为正三轮摩托车运行整个试验循环工况的逐秒(1 Hz)统计量，运行完6个市区试验工况循环后，样本数据总量为1 170组。为保证神经网络得到充分训练，将样本数据随机分成3组，其中随机抽取100组样本数据作为测试集，剩余1 070组数据中随机抽取80%作为训练集，20%作为验证集。

2.2 BP神经网络的基本原理

BP神经网络是由一种3层及以上神经元所组成的多层网络。其基本结构如图2所示。在图2中，样本数据[x1，x2，…，xn]依次经过输入层、隐含层与输出层，最终在输出层得到[y1，y2，…，yk]的信息输出。

如图3所示，在BP神经网络的训练过程中，数据首先沿着输入层-隐含层-输出层的顺序进行前向传播，如果得到的输出值与理想的输出值误差没有达到预定值，其误差就会从相反的方向反向传播。传播的过程中，各层之间的权值与阈值重新得到调整与更新(图2中各层之间权值分别为V、W)。然后神经网络重新进行前向计算，如此不停的迭代直到误差值达到预定值最终输出数据[8]。

图2 BP神经网络的基本结构

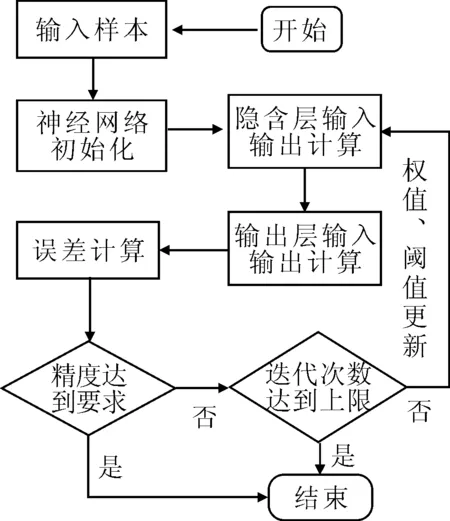
图3 BP神经网络的训练流程

2.3 BP神经网络的结构设计

2.3.1 输入层与输出层的设计

预测模型输入选择的好坏对于模型预测准确与否影响很大，若输入和输出之间具有一定的相关性，模型的预测准确性可以得到提高[9]。在本文中，预测模型的输出为CO、NOx以及THC的排放浓度，因此应当选取与模型输出紧密相关的参数作为输入。

影响排放的参数众多，其中，车速与加速度能够显著反映驾驶员操纵行为并且与污染物排放浓度模切相关，可以作为衡量排放物排放浓度的两个重要参数[10]。已有的研究表明点火性能与过量空气系数λ是影响小型汽油机的两个主要参数，其中过量空气系数λ是最为主要的影响因素[11]。因此，笔者选择车速、加速度与λ值作为排放预测模型的输入。

2.3.2 网络层数

通常采用多层的神经网络结构来解决各种实际问题，但神经网络的层数并不是越多越好，层数越多意味着更加复杂的网络结构，这会导致神经网络在计算时收敛的速度变得更慢。神经网络的层数过多有时甚至会使神经网络的输出性能变差，出现“过拟合”现象[12]。因此在大多数使用BP神经网络的案例中，采用的都是单隐含层或者双隐含层的结构，鲜有更大的隐含层数。笔者采用具有双隐含层的4层神经网络结构。

2.3.3 数据预处理与激励函数选择

将输入数据归一化到[-1，1]区间可以加快神经网络的训练收敛速度，同时也要对输出数据进行反归一化处理[13]。归一化的计算公式为：

(1)

反归一化计算公式为：

(2)

式中：x(i)为第i个输入参数的归一化后数值；xi为第i个输入参数的样本值；ximax为第i个输入参数的最大样本值；ximin为第i个输入参数的最小样本值；y(j)为第j个输出参数的反归一化后数值；yj为第j个输出参数的样本值；yjmax为第j个输出参数的最大样本值；yjmin为第j个输出参数的最小样本值。

当神经网络结构为4层时，一共有3个激励函数，为了保证神经网络的非线性，3个激励函数依次选用两个双曲正切“tansig”函数和一个“purelin”线性函数。

2.3.4 隐含层节点数

确定隐含层节点数在整个BP神经网络的结构确定中是十分重要的一环。选择合理的隐含层节点数可以使得神经网络具有较好的泛化能力[14]，在神经网络训练中可有效避免出现“过拟合”现象。通过式(3)确定隐含层节点数：

(3)

式中：m、n分别为输入层、输出层神经元个数；a为1到10之间的任一常数。

以式(3)为基础，逐次尝试各种隐含层节点数组合，经过多次仿真试验，最终根据神经网络的均方误差确定的BP神经网络结构为3-7-2-2。

2.4 粒子群优化算法

2.4.1 算法基本原理

粒子群优化算法是一种受鸟类捕食过程启发的群体智能优化算法[15-16]。粒子群算法的基本原理为初始化一群粒子，每个粒子都被当作优化问题的一个可行解，并且都具有位置和速度特征，适应度函数则根据具体的优化问题解空间决定。粒子在寻求全局最优解时，通过对个体极值与全局极值的跟踪来更新自身的速度和位置，更新方程分别为：

(4)

(5)

2.4.2 PSO对BP神经网络的优化

PSO对BF神经网络的优化思想是通过粒子群算法优化BP神经网络的初始权值与阈值，将经过充分训练的参数作为BP神经网络的初始值从而提高模型的预测能力，基本步骤如图4所示。

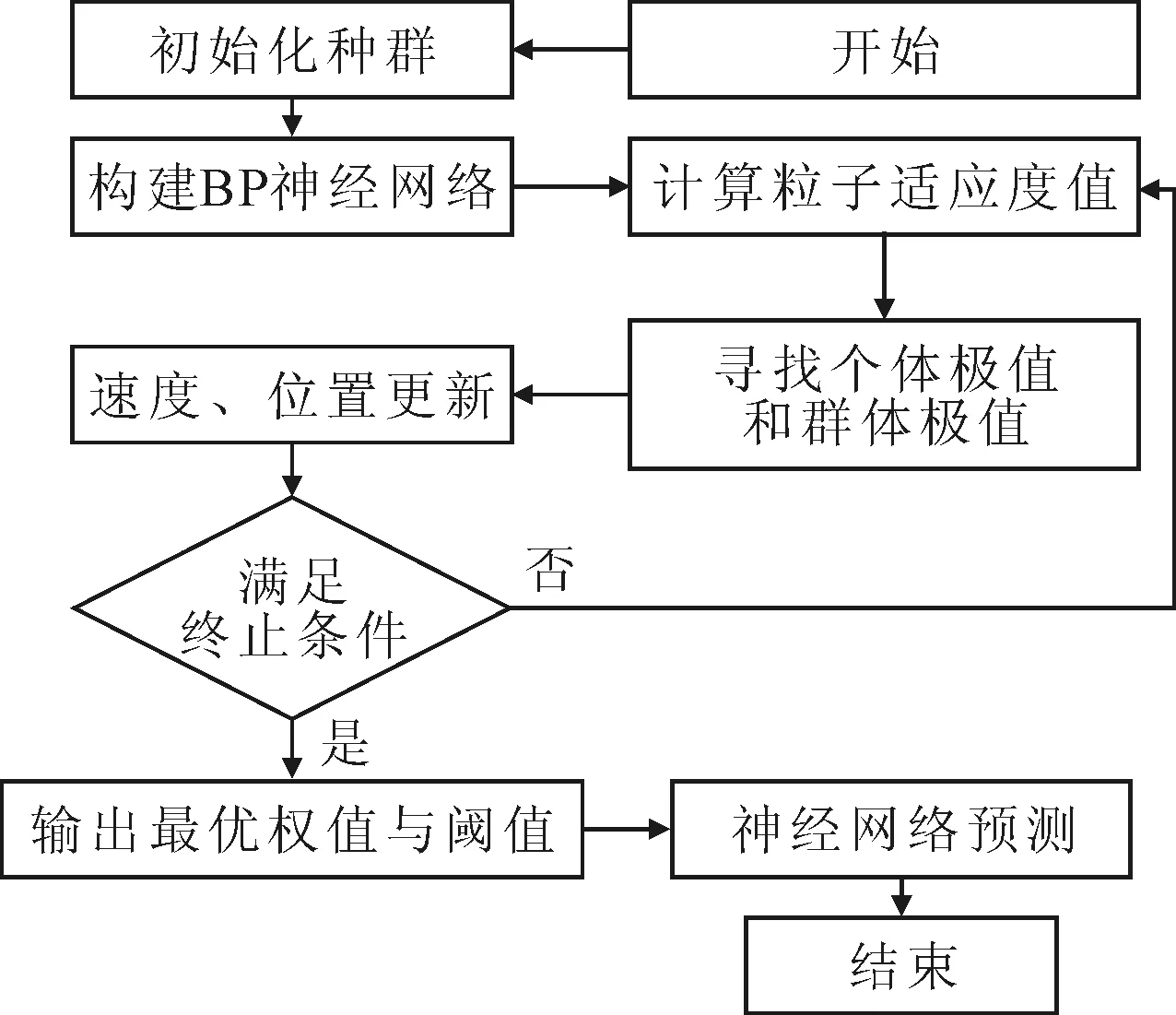
图4 PSO-BP神经网络训练流程

3 预测结果

将样本数据导入，采用PSO-BP神经网络预测模型进行训练，经过训练学习后，选取100个样本进行测试，预测结果如图5～图7所示。

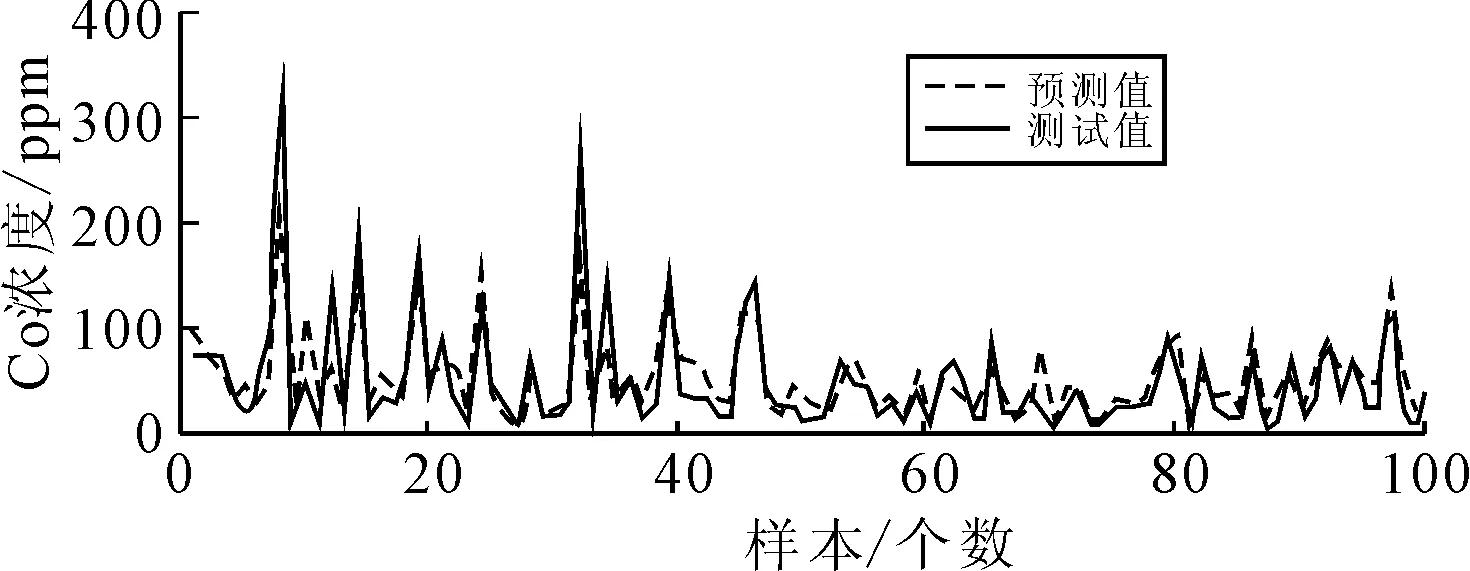
图5 CO排放浓度预测结果

图6 NOx排放浓度预测结果

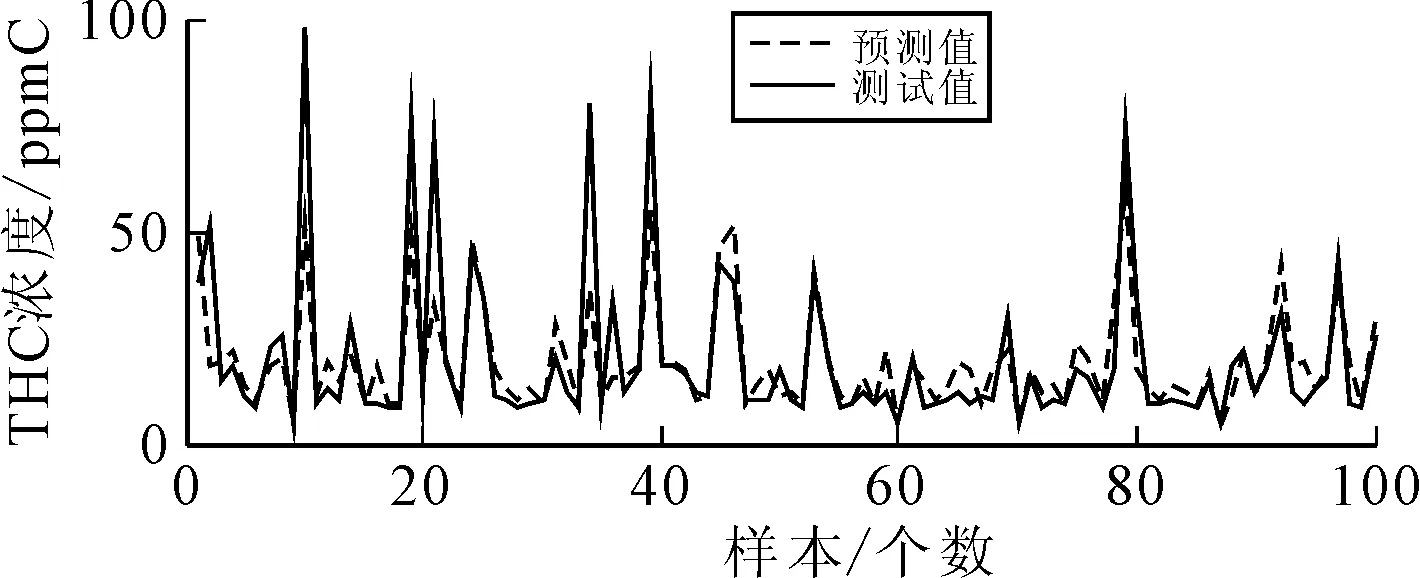
图7 THC排放浓度预测结果

从图5～图7中可知，虽然在图中某些波峰波谷处，样本数据变化很大，预测模型响应较慢导致了CO、NOx、THC排放浓度的预测值与实际测量值存在较大的误差。但在整体上，CO、NOx、THC排放浓度的预测值与其实际测量值走势基本一致，能够较好地预测摩托车在不同工况下的排放特性。

通过比较选取的摩托车工况点的排放因子的实际测量值与预测值的总体相对误差来验证预测模型的准确性。比较结果如表3所示。

表3 排放因子比较

从表3可知，CO、NOx、THC的排放因子的实际试验值与预测值的总体相对误差分别为6.90%、8.32%和2.23%，误差均在9%以下，这说明在一定允许误差范围内，模型的预测结果是较为可信的。

此外，引入斯皮尔曼相关系数来验证CO、NOx、THC排放浓度的预测值与实际测量值的相关程度。斯皮尔曼相关系数计算公式为：

(6)

式中：N为样本个数；Xi、Yi分别第i个样本的预测值与实际测量值。

根据式(6)计算CO、NOx、THC排放浓度的预测值与实际测量值的斯皮尔曼相关系数分别为0.832 3、0.851 1和0.841 5。运用PSO-BP神经网络预测的CO、NOx、THC排放浓度与实际测量值相关程度强，排放预测模型的泛化能力较好。

4 结论

摩托车尾气污染物排放浓度的影响因素众多，引入了基于PSO-BP神经网络摩托车排放预测模型，该排放预测模型以双隐含层BP神经网络为基础，使用粒子群算法优化神经网络的权值与阈值。结果表明基于PSO-BP神经网络的摩托车排放预测模型的预测精度高，具有良好的泛化能力，能够较好地预测该款车型不同工况下的排放特性。