神经电极组合参数对脑组织微动损伤影响研究
尹雪乐,张文光,于 谦
(上海交通大学 机械与动力工程学院,上海 200240)
植入式脑部神经电极是连接神经组织和外部电子设备的关键部件,它不仅广泛应用于神经电信号的录制,还可以实现神经电刺激,在治疗癫痫、中风、帕金森症及脊髓损伤等疾病的临床应用中具有广泛的应用前景[1]。目前,神经电极的应用面临长期稳定性差、使用寿命短的技术难题。神经电极在植入脑组织后,植入初期都正常工作,但在较长时间内即发生失效。这是由于电极植入时对脑组织造成的植入损伤[2],以及植入后脑组织微动带来的微动损伤[3],均会激发组织的免疫反应,在电极表面产生组织包裹,最终阻断了神经电极与神经元之间的电信号传输,导致电极失效。研究表明,微动损伤是导致组织包裹和电极失效的最关键因素[4-5]。因此,有效减少电极植入后的微动损伤,是延长电极寿命的主要手段之一,已成为当前神经电极研究的热点。
电极与脑组织间的微动环境比较复杂,研究表明,其相对微动主要由3 个因素产生[6-7]:生理因素、机械因素和行为因素。生理因素主要是指心脏跳动节律变化,以及呼吸频率变化而产生的脑血管压力;机械因素是指通过外部设备与颅骨传递给电极的振动;而行为因素指头部或整个身体的运动。在各种因素中,以生理因素引发的纵向微动产生的危害最大。因此,在研究电极与脑组织相对微动造成的组织损伤时,本文主要研究纵向位移(沿电极植入方向)引发的微动损伤。
目前,为有效抑制微动造成的组织损伤,国内外学者致力于优化神经电极的力学性能、形状结构及其与脑组织的物理耦合度。如目前大多数研究采用柔性材料代替硅基电极,以降低电极刚度,从而改变电极与组织间的力学匹配性[8-9]。有研究表明,电极的形状结构对脑组织微动损伤具有非常显著的影响[10-11]。Zhu 等[12]通过建立电极−脑组织三维仿真模型,考察了电极与组织间不同物理耦合度(摩擦系数)对微动模式下应变场的影响。作者之前研究了电极的各个参数与脑组织微动损伤的关系[6,13],但这些研究多集中在神经电极单参数因素的改变对脑组织损伤的影响,而对神经电极多个参数的相互关系及各个因素的敏感性研究甚少。因此,本文将对神经电极的多个参数的影响程度及其综合影响进行研究,为电极的最优化设计奠定基础。
由于神经电极−脑组织接触界面的复杂性,难以通过精确的动物实验来衡量脑组织的微动损伤,有限元仿真法是目前研究微动损伤最有效的手段之一。利用有限元软件对脑组织−神经电极的相对微动过程进行仿真分析,并通过脑组织微动过程的最大主应变平均值来反映微动过程中脑组织损伤的程度。
正交试验设计法是研究多因素多水平的一种设计方法,它是根据正交性从全面试验中挑选出部分有代表性的点进行研究,这些有代表性的点具备均匀分散、齐整可比的特点。正交试验设计法是高效处理多因素优化问题的主要方法[14]。
本文基于被广泛应用于临床的硅基单柄电极(NeuroNexus 公司生产,型号A1×16−3 mm−50−177),运用正交试验设计思想,进行一系列有限元仿真,研究神经电极的5 个基本参数[13](针尖圆角、楔形角、电极厚度、刚度及表面摩擦系数)对脑组织微动损伤的综合影响,并揭示各因素的影响程度及最优组合,为神经电极的最优化设计和进一步降低微动损伤提供参考依据。
1 方 案
1.1 神经电极−脑组织模型
采用SolidWorks 2014 三维建模软件建立神经电极−脑组织模型。整个装配体模型关于XY 平面和YZ 平面对称,为提高计算效率,采用1/4 对称模型,如图1(a)所示。

图1 神经电极和脑组织仿真模型Fig.1 Finite element models of the neural electrode and brain tissue
电极模型基于广泛应用于临床的硅基单柄电极(NeuroNexus 公司生产,型号A1×16−3 mm−50−177)建立,图1(b)为该电极的3 个基本形状参数,针尖圆角R,楔形角α 和电极厚度h。同时,大脑的几何模型也可合理简化。由于脑组织产生微动损伤的区域通常在电极周围数百微米范围内[15],为了对敏感区域进行限制,将脑组织模型的边界与电极中心线距离定义为750 μm,将微动产生的所有应变场都包含在内,消除边界效应的影响。
由于脑组织与电极的相对微动可以看作是随时间变化的位移载荷,因此,采用瞬态动力学分析来对电极−脑组织微动过程进行仿真。采用ANSYS Workbench 15.0 的Transient Structural 瞬态动力学模块进行有限元分析。
在对电极和脑组织材料进行定义时,电极采用硅基电极,将硅视为线弹性材料,弹性模量设置为200 GPa,泊松比为0.278,密度为2.34 g/cm3。电极植入脑组织的位置为大脑皮层,与大部分生物材料相似,它具有弹性与粘性。研究证明,脑组织微动产生的变形是大应变变形(应变超过了5%)[15],因此,广泛采用超弹性本构模型来描述脑组织的力学特性。采用Ogden 超弹性本构模型和Prony 级数定义的粘弹性本构模型来描述脑组织特性。脑组织材料参数如表1 所示。μ 和a 为由试验数据拟合确定的材料常数,G,G2为松弛系数,T,T2为松弛时间。

表1 脑组织材料参数[16]Tab.1 Material properties of the brain tissue
对电极和脑组织划分网格,采用六面体单元,单元尺寸设置为0.08 mm。为使仿真结果更加精确,对电极−脑组织接触区域进行网格细化,单元尺寸细化至0.03 mm。
由于采用电极−脑组织的1/4 对称模型,故对模型XY 平面和YZ 平面设置对称约束。在仿真初始状态,电极与脑组织紧密接触,在创建界面接触时,将电极设置为目标面,脑组织设置为接触面。由于电极与脑组织间具有粘附作用,接触类型选择摩擦接触,接触算法采用增广拉格朗日乘子法。由于大脑皮层往下延伸通过脑干连接至脊髓,大脑的运动受到限制,因此,在定义边界条件时,脑组织应固定下表面,而将上表面设为自由面。
在脑组织微动中,呼吸、心脏跳动等生理因素引发的纵向微动产生的影响最大,因此,主要考虑纵向位移引发的微动损伤。参考Gilletti 等[7]测定的实验结果,由呼吸产生的脑组织微动幅值为2~25 μm,频率约为1~2 Hz,而由心脏跳动产生的组织微动幅值约为1~4 μm,频率可至 5 Hz。因此,用幅值10 μm,频率4 Hz 的正弦位移载荷模拟脑组织微动状态,施加于电极的上表面,并将微动时间设置为0.5 s。
1.2 微动损伤评估标准的建立
根据以往研究,当脑组织损伤较大时,其应变值也会相应较大,因此,普遍采用最大等效应力或最大等效应变作为脑组织微动损伤评估标准[17-19]。这一标准的局限性在于模型中的最大值反映的只是某一时间点脑组织的局部力学状态,而微动损伤是连续微动的累积结果。且根据Karumbaiah等[19]的试验结果,当脑组织应变在5%以上时,会有大量星形胶质细胞及神经元死亡,激发免疫反应。可由此推知,最大应变值的降低仅表明脑组织局部损伤减少,并不能全面衡量连续微动过程的组织受损程度。目前还没有一种可以客观、全面地衡量脑组织微动损伤的评估标准,因此,本文建立了一种更为客观地反映脑组织损伤的评价方法,为数值仿真过程中衡量组织损伤提供了参考依据。
为了更为客观全面地考察微动过程脑组织损伤的分布情况,对神经电极微动过程的仿真结果进行分析,将微动过程划分为20 个时间步,提取了各个时间点脑组织所有节点的应变值(约46 000个节点),并作出了时间−节点−应变的三维分布图,如图2(a)所示。由图中可以看到,脑组织各个节点的应变变化规律基本一致,只是不同节点的应变值不同。且由图2(b)仿真应变云图可知,脑组织损伤主要集中在电极针尖接触区域。因此,提取应变值最大的节点,采用该节点微动过程中的应变值近似评估脑组织的整体损伤程度,对该节点处20 个时间点的应变值取平均值,作为本文中脑组织损伤的评估标准。
1.3 正交仿真设计

图2 脑组织应变分布图Fig.2 Distribution of the brain tissue strain
为了研究神经电极的5 个常用参数[13](针尖圆角、楔形角、电极厚度、刚度及表面摩擦系数)对脑组织微动损伤的综合影响,采用正交试验的思想设计了一系列数值仿真。共考察了5 种因素,每种因素包含3 种水平,依照L27(35)正交表设计方案进行了27 组仿真,并将微动过程中的最大主应变平均值作为结果指标。表2 为各因素水平表,各因素水平值是在各参数的常用范围内等差取值确定,具有较强的代表性。其中,A 代表针尖圆角,B 代表楔形角,C 代表电极厚度,D 代表电极刚度,E 代表电极表面摩擦系数。
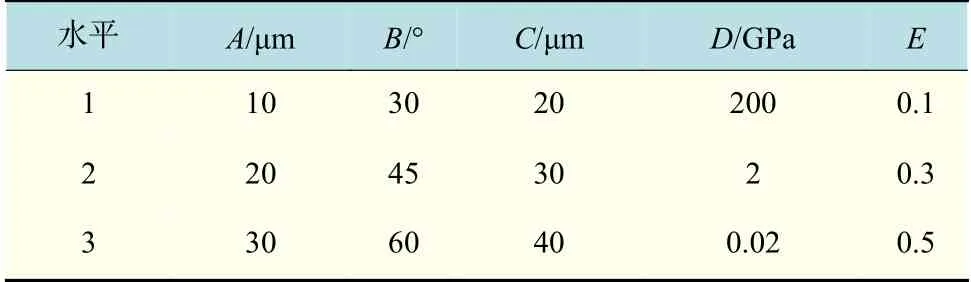
表2 因素水平值Tab.2 Value of parameters of different levels
在多因素试验中,不仅因素对指标有影响,而且因素之间的联合搭配也会对指标产生影响。因素间的联合搭配对试验指标产生的影响作用称为交互作用。在考虑多因素对结果的影响时,还应考虑各因素之间是否有交互作用。当电极采用不同刚度的材料时,其表面摩擦系数会发生相应变化,因此,应当考察刚度和摩擦系数的交互作用。另外,电极的尺寸也会显著影响电极植入后的长期性能[20],考虑到植入电极的硬度,杨氏模量并不是唯一重要的变量,应该同时考虑杨氏模量和电极尺寸。因此,也研究了电极厚度与其刚度(杨氏模量)的交互作用,以探究其对脑组织损伤的综合影响。
2 仿真结果分析
2.1 直观分析
直观分析法,又称极差分析法,通过对某一因素各个水平的指标平均值及其极差进行综合比较,可以得到最佳配比及各因素影响程度。表3为脑组织应变的直观分析结果。kj为第j 水平所对应的试验指标平均值。由kj的大小比较可以判断该因素的优水平。R 为各因素的极差,反映了该因素水平波动时试验指标的变动幅度,R 越大,说明该因素对试验指标的影响越大。根据R 的大小,可以判断各因素对试验结果影响的主次顺序。

表3 脑组织应变直观分析Tab.3 Intuitive analysis of the brain tissue strain
由表3,通过各因素的极差大小可知,各因素对脑组织损伤影响的主次顺序为A−B−C−E−D,A,B 为主要影响因素,D 为不重要因素。这说明在微动过程中,神经电极的圆角和楔形角大小对脑组织损伤具有显著影响,而电极刚度的改变对脑组织损伤影响不大。各因素的最优组合为A2B2C3D1E3,即电极参数为圆角20 μm,楔形角45°,厚度40 μm,杨氏模量200 GPa,摩擦系数0.5。
图3 为各因素水平变化时脑组织应变值的变化趋势。由图3 可知,脑组织应变随着电极圆角的增加先降低后升高,在圆角20 μm 处达到最小值。组织应变随楔形角的变化也具有相同的规律,在45°时取得最小值。另外,脑组织微动损伤与电极厚度及表面摩擦系数近似于线性关系。当电极厚度增加时,电极表面摩擦系数增大时,电极与脑组织的力学匹配性及物理耦合度增强,因此,有助于降低微动损伤。电极刚度对脑组织微动损伤的影响不大,可以忽略,但考虑到植入所需刚度,硅基电极为最佳选择。
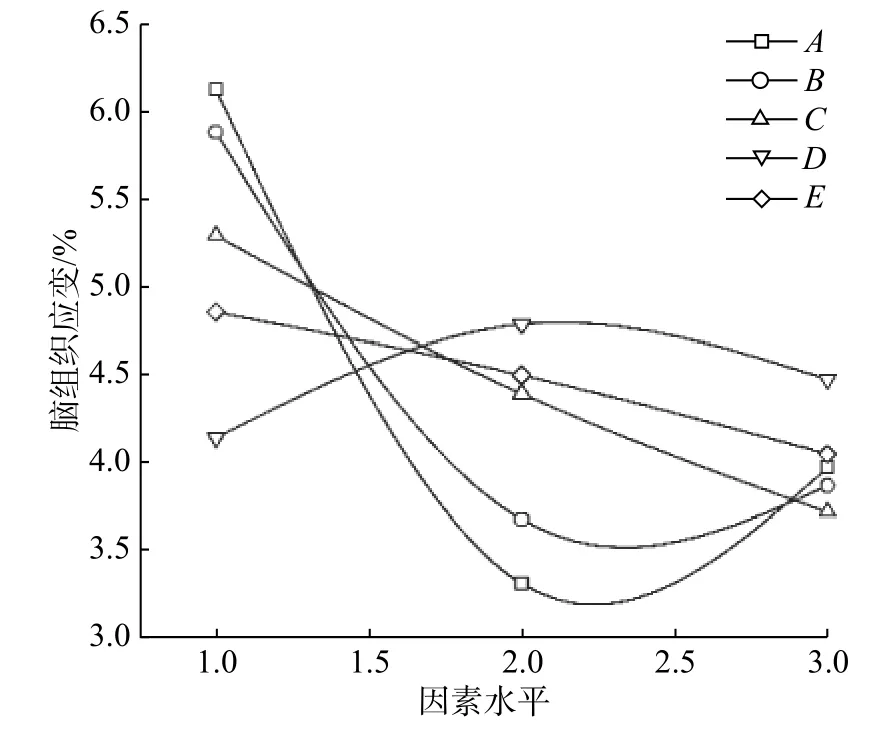
图3 脑组织应变随各因素不同水平值的变化趋势Fig.3 Changes of the brain tissue strain with different levels of parameters
2.2 显著性检验(方差分析)
为了探究各因素对仿真结果的影响大小,判断所考察因素的影响作用是否显著,同时研究两个交互作用对结果的影响程度,对以上正交仿真结果进行了方差分析。表4 为脑组织应变的方差分析结果。其中,df 为因素自由度,SS 为因素平方和,MS 为各因素方差。对该结果进行了F 检验,通过对P 值进行分析,即可得到各因素的影响作用。
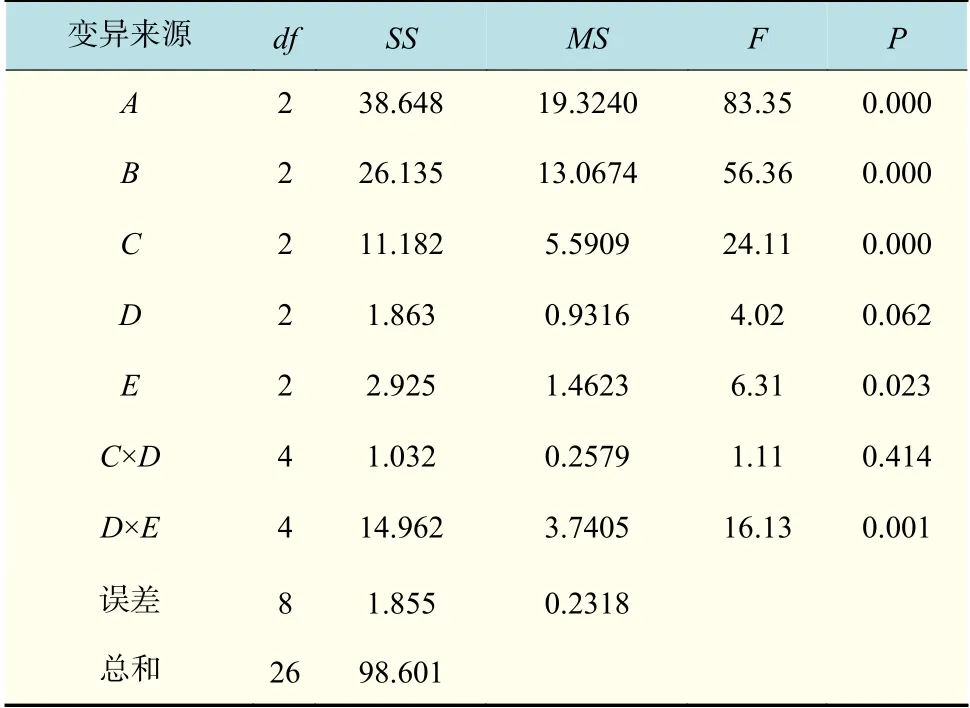
表4 脑组织应变方差分析Tab.4 Analysis of the variance of the brain tissue strain
由表4 中的数据可知,P(A),P(B),P(C)<0.001,P(D)>0.05,P(E)<0.05,即电极圆角、楔形角及厚度对脑组织损伤具有显著影响,电极表面摩擦系数对组织损伤具有一定的影响,而电极刚度对组织损伤影响不大,这与前文直观分析结果基本一致。另外,从显著性检验结果中可以看到,P(C×D)>0.05,P(D×E)<0.01。图4 为电极刚度与摩擦系数和电极刚度与厚度的交互作用图,当各个图线平行时,代表两种因素无交互作用。因此,可以判断,厚度与刚度的交互作用对脑组织损伤没有显著影响,可以忽略。而电极刚度与其表面摩擦系数的交互作用对脑组织损伤具有显著影响。
综合直观分析和方差分析,各因素及交互作用的影响主次顺序为A>B>C>D×E>E>D>C×D。由表5 的D×E 二元表可知,D×E 的最优组合为D1E1,故五因素的最优组合为A2B2C3D1E1,即电极的最优参数应选择圆角20 μm,楔形角45°,厚度40 μm,杨氏模量200 GPa,摩擦系数0.1。

图4 因素间的交互作用图Fig.4 Interaction between factors

表5 D×E 二元表Tab.5 Brain tissue strain of D×E
3 结 论
a.为了更为客观全面地考察微动过程脑组织损伤的分布情况,给出了时间−节点−应变值的三维分布图。提取应变值最大的节点,采用该节点微动过程中的应变值近似评估脑组织的整体损伤程度。对该节点处20 个时间点的应变取平均值,作为脑组织损伤的评估标准。
b.脑组织应变随着电极圆角的增加先降低后升高,在圆角20 μm 处达到最小值。组织应变随楔形角的变化也具有相同的规律,在45°时取得最小值。另外,脑组织微动损伤与电极厚度及表面摩擦系数近似于线性关系。当电极厚度增加时,电极表面摩擦系数增大时,电极与脑组织的力学匹配性及物理耦合度增强,因此,有助于降低微动损伤。电极刚度对脑组织微动损伤的影响不大,但考虑到植入所需的刚度,硅基电极为最佳选择。
c.通过显著性检验可知,电极圆角、楔形角及厚度对脑组织损伤具有极为显著的影响,电极表面摩擦系数对组织损伤具有一定的影响,而电极刚度对组织损伤影响不大。厚度与刚度的交互作用对脑组织损伤没有显著影响,可以忽略。而电极刚度与其表面摩擦系数的交互作用对脑组织损伤具有显著影响。
d.综合直观分析和方差分析,各因素及交互作用的影响主次顺序为A>B>C>D×E>E>D>C×D。五因素的最优组合为A2B2C3D1E1,即各电极参数应选择圆角20 μm,楔形角45°,厚度40 μm,杨氏模量200 GPa,摩擦系数0.1。
研究结果表明,电极的各个参数对脑组织微动损伤具有重要影响。对电极的形状及力学参数进行合理设计,可以有效地降低脑组织微动损伤和组织包裹,明显改善电极−脑组织界面的力学状态和界面耦合,这为神经电极的最优化设计提供了参考依据,有助于提高电极的长期稳定性。

