运用改进的萤火虫算法求解TFT-LCD 单元装配调度问题
李瑞婷,叶春明,吴思思
(上海理工大学 管理学院,上海 200093)
TFT−LCD(thin film transistor-liquid crystal display)即薄膜晶体管液晶显示器(液晶面板),近些年以其屏幕亮度高、制造费用低及分辨率高等优势普遍应用于手机、显示器、平板电脑、台式电脑、电视及电子手表等各类显示领域。TFT−LCD具有性能优良、功耗低、视角宽、价格低廉、发展空间较大等诸多优点,是现代人类不可或缺的重要部分,也是促进现代化全球经济增长的亮点。但是,在大批量生产加工过程中,TFT−LCD 也存在着一些需要重视的问题,由于TFT−LCD 的广泛应用,市场的需求量剧增,如何优化生产,提高效率的同时保证产品质量,将是一个至关重要的问题。
结合上述关于TFT−LCD 的生产特点,提高其生产效率迫在眉睫。TFT−LCD 的生产流程具体包括以下3 个关键步骤:薄膜晶体管阵列制造阶段(Array)、液晶面板组装制造阶段(Cell)、液晶模组组装制造阶段(Module)。在不同阶段的生产加工过程中,同一产品的加工工艺并不相同,对于不同产品所需要的加工工艺阶段也各不相同。单元装配阶段作为TFT−LCD 生产制造过程中的一个关键环节,如何保持单元装配阶段生产线的平衡以及提高其生产效率对整个TFT−LCD 生产线具有至关重要的作用。本文主要研究TFT−LCD 的单元装配阶段的调度问题。
TFT−LCD 的单元装配调度问题通常看作为混合流水车间调度问题。混合流水车间问题是建立在流水车间问题基础之上的,它只有在满足特定约束条件下,通过合理地分配各个加工工艺并行机的全部任务,使调度指标达到最优。侯丰龙等[1]研究了TFT−LCD Module 阶段的调度问题,考虑了不同学习因子和遗忘因子对最大完工时间的影响,在此基础上建立了数学模型,并运用布谷鸟算法对模型进行求解。汤洪涛等[2]对于混合车间调度问题,将最小化最大完工时间作为调度目标,并引入多Agent 协商机制和模拟退火算法与免疫算法相结合的方法,提出了基于分解策略的免疫遗传算法。扈静等[3]以追求装配线平衡为研究目标,设计了基于激素调节机制的改进遗传算法。王福吉等[4]为了运用字符串编码方法来确定解空间的范围,设计了一种基于可行域搜索的遗传算法。吴晖[5]针对Array 制造系统的高度不确定性特征,建立了Array 制造系统的仿真模型,并对第五代TFT−LCD 车辆调度问题进行了研究。Kahraman等[6]提出了平行贪婪算法求解多处理机任务多阶段混合流水车间调度问题。
本文对TFT−LCD 的单元装配生产线的混合流水车间调度问题展开研究,并讨论了随着学习因子和遗忘率的变化,工件的加工时间也会受到影响。Biskup[7]首次将学习效应引入到调度领域,他认为影响学习效应的2 个因素为加工位置和学习效应因子。Mosheiov 等[8]在Biskup 的基础上研究了工件学习曲线调度模型,并且将学习因子作为随工件种类的不同其学习因子也不同的量。Rudek[9]证实了同时具备学习效应和遗忘效应的单机器或双机器车间调度问题都是NP−hard(nondeteministic polynomial)。
综上所述,将学习遗忘效应引入生产调度的研究并不多,目前学者们的研究主要集中在单机器或者双机器的学习遗忘效应的流水车间调度问题上。据此提出将学习遗忘效应加入多机器的混合流水车间调度问题中,研究其对目标函数的影响。萤火虫算法是由剑桥学者Yang[10]在2005 年提出的,他提出这个算法的灵感来自自然界中萤火虫在夜晚会发光这一独特现象。萤火虫算法具有适合并行处理、流程简单及稳定性强等特点,被广泛应用于函数优化、路径规划及社会科学等多个领域,但是,标准的萤火虫算法也有其弊端,本文运用改进的萤火虫算法来求解TFT−LCD单元装配调度模型,并与其他算法进行比较,验证了改进的萤火虫算法的合理性和优越性。
1 模型描述
1.1 TFT−LCD 单元装配工艺流程
TFT−LCD 单元装配工艺在整个TFT−LCD 生产过程中起到了承上启下的作用。它的生产线类型等同于混合流水装配作业生产线,在混合流水装配作业生产线中,工件的装配过程可以采用并联的加工方式,也可以采用串联的加工方式。在实际加工生产中,带生产支线的装配作业调度其实就是一种并联方式的生产调度。TFT−LCD 单元装配工艺的流程图如图1 所示。
如图1 所示,单元装配是指将阵列制造阶段加工完成的TFT 玻璃基板和滤光片基板进行层层压合,随后对基板进行切割,并将液晶材料充入两块基板之间,最后再进行检验的工艺流程。其完整的工艺流程包括如图1 所示的11 道工序,TFT 玻璃基板的PI 涂布、定向摩擦、框胶形成、彩色滤光片的PI 涂布、定向摩擦、隔离子散布,再将经过上述工艺加工好的TFT 玻璃基板和彩色滤光片进行对位粘合、根据客户需要的尺寸切割、真空除去液晶空盒中的空气、注入液晶、封口、偏振片粘附,最后进行通电检查。
1.2 TFT−LCD 单元装配调度模型
现对如图1 所示的TFT−LCD 单元装配调度问题进行描述。

图1 TFT-LCD 单元装配工艺流程Fig.1 Cell stage process flow chart
有若干种不同类型的工件,它们由零件M 和零件N 分别经过若干不同加工工艺后,最终装配成工件Φ,在现实生产中将批(lot)作为生产的基本单位,任何一批工件都由许多相同工件组成,约束条件:
a.工件一旦开始加工就不允许中断;
b.同一工件加工路径是确定的,不同工件工序间加工顺序不分先后;
c.忽略设备生产过程中可能出现的损坏延误问题;
d.不考虑次品返工问题;
e.同一机器连续生产的两批工件不属于同种类型,不考虑设备准备时间;
f.机器一批只能加工一种工件。
1.3 数学模型和参数设定
目标函数

式中:Tmax为最小化最大完工时间;Tt为最小化加权延迟时间;Tij为机器的完工时间;dij为工件Jij的交货时间;wij是工件Jij的延迟权重。
为了后续求解简便,将其转化为单目标处理,即令 f1(x)=Tmax,f2(x)=Tt,故
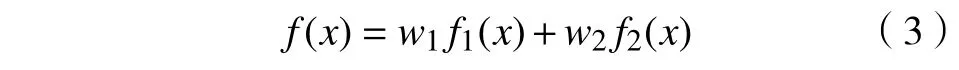
式中,w1,w2为自定义参数,取值为[0,1],且w1+w2=1。

约束条件:式中:n 为工件种类总数;Ei表示第i 种工件种类,i =1,2,···,n,由于每种工件由零件M 和零件N组装而成,Ei为零件M 批装配产品;Ei*为零件N 批装配产品;Ei+为零件M 批和零件N 批的装配产品;Jij为工件种类Ei的第j 批工件,j =1,2,3,···,hi;hi表示第i 种工件的等待加工工件总批量;Ok表示第k 道工序,k=1,2,···,c,c+1,···,z,z+1,···,s;1到 c, c+1到 z, z+1到s 分别表示零件M,零件N 及装配后零件的加工工序;指工序Oik的开始时间;Pijk,分别表示一般加工时间以及工序Oik的完工时间; Yi,j,k,m为决策变量。

式中,Mkm为第k 道工序的第m 台机器。
式(1)表示目标函数为最小化最大完工时间;式(2)表示全部工件的加权延迟时间最小;式(3)表示将多目标问题转换为单目标问题处理;式(4)表示任一工件只允许在一台机器上加工;式(5)表示一台机器同一时刻只允许加工一批工件;式(6)表示零件M 前一道工序的总批数必须不少于后一道工序总批数;式(7)表示零件N 后一道工序总批数不多于前一道工序总批数;式(8)和式(9)表示装配工序R 的总批数必须少于M 工件批和N 工件批的总批数;式(10)和式(11)表示装配时M 批工件和N 批工件必须在同一机器上加工,且同时开始加工;式(12)表示每个工件必须要按照既定的先后顺序进行加工。
2 改进的萤火虫算法
2.1 萤火虫算法描述
萤火虫算法[11-12]作为一种新兴的元启发式群智能算法,目前主要应用于解决优化问题,但是,随着科学技术的发展和研究的深入,它将会运用到各个领域。该算法源于自然界萤火虫在晚上的聚集活动并自身发光的自然现象而产生的,并且有效地描述了萤火虫自身亮度的变化以及吸引度的大小,通过模拟萤火虫凭借亮度与吸引度去寻找它的伙伴这一类本能行为,实现了优化目标函数的目的。萤火虫算法作为仿生群智能算法的一种,主要由2 个关键因素所决定,即自身发出光的亮度和它吸引同伴的能力。萤火虫自身发出亮光的大小决定了个体所在位置的优越性及其运动的方向,其运动的距离和它吸引同伴的能力有关,随着亮度和吸引力的不断刷新,从而实现目标函数值优化的过程。现描述其优化原理。
定义1萤火虫的相对荧光亮度

式中:I0表示个体所在位置的最大荧光亮度;γ 是光强吸收系数,也可以将它设定为常数;rij是个体i 与个体j 之间的空间距离。
I0和目标函数值呈正相关关系。若目标函数值越优,那么,萤火虫亮度就越高。
定义2萤火虫的吸引度

式中:β0表示2 个萤火虫彼此之间距离等于零时萤火虫i 对萤火虫j 的吸引力。
定义3萤火虫i 被吸引向萤火虫j 移动的位置更新

式中:xi,xj是萤火虫个体i 和j 所处的空间位置; ∂是步长因子,为[0,1]上的常数;rand 为[0,1]之间均匀分布的随机数。
2.2 混沌萤火虫算法
通过大量研究表明,当初始的萤火虫算法经过反复迭代寻优接近尾声时,大部分萤火虫都聚集在局部以及全局极值点附近,随着距离的逐渐减小,萤火虫之间的吸引力逐渐变大,这种情况将会导致算法的局部寻优能力下降,在算法迭代次数有限的情况下,无法达到精度的要求。综上所述,基本的萤火虫算法容易陷入局部最优,一旦到达局部最优极值点附近,算法出现了收敛速度慢且在极值点附近震荡的问题。为解决此类问题,提高算法的寻优精度,利用混沌运动的普遍性、随机性等特点,在萤火虫算法的基础上,引入了混沌思想,从而提高萤火虫种群的多样性和寻优的遍历性。
2.3 算法改进
混沌是普遍存在于非线性系统中的一种现象,具有随机性、规则性及遍历性等特点,能在其取值范围内按其自身规律不重复地历经所有可能状态,所以,混沌搜索是一种新颖并且高效的优化工具。混沌搜索的原理:通过某个特定格式迭代产生混沌序列,然后通过载波的方式将其引入优化空间。相关研究表明,逻辑自映射函数易于计算,且其生成的混沌序列遍历性较常用的Logistic 映射更优[13]。因此,本文选用逻辑自映射函数产生混沌序列,待寻优问题的数学表达式为

式中:ni表示n 类粒子第i 个个体;表示第*维的个体ni。
个体ni处于多维空间内,将ni在第q 维的位置表示为,则∈(,)。表示在第q 维的第i 个A 类粒子,wiq表示在第q 维的第i 个w 粒子。由于定义域限制,使用式(17)将xi的所有搜索空间维度映射至定义域(−1,0)∪(0,1)


得到经过载波操作后的混沌变量序列,再使用式(18)将其映射回原空间。

此时,对新个体进行评价。若对应的函数值更优,则保留该个体;否则,直接进行下轮混沌搜索,直至达到混沌搜索次数。改进的混沌萤火虫算法的主要步骤如图2 所示。

图2 混沌萤火虫算法流程图Fig.2 Improved firefly algorithm flow chart
2.4 算法复杂度分析
算法复杂度是评估算法性能的一个重要指标,它决定了算法的执行效率,并且在很大程度上影响着计算机的求解能力。由上面的算法流程容易看出,改进的萤火虫算法花费的计算时间主要在算法的迭代进化过程中。假设求解问题的问题规模为D,种群规模为Q,迭代次数为W。在每一次的进化迭代过程中,算法主要的计算量包含萤火虫位置更新与局部邻域搜索两部分。在萤火虫位置更新部分,对种群中的萤火虫进行共30 次的位置更新操作,且每10 次取一个平均值。其最复杂情况下的最大计算时间复杂度为3WO(QD),计算适应度值以及保留最优个体的时间复杂度分别为WO(QD)和WO(Q),所以,该部分总的计算时间复杂度为4WO(QD)+WO(Q);在局部邻域搜索部分,需要对种群中30%的萤火虫进行混沌搜索,最大的时间复杂度为0.3WO(QD),计算适应度值及保留最优个体的计算时间复杂度分别为0.3WO(QD)和0.3WO(Q),所以,该部分总的计算时间复杂度为0.6WO(QD)+0.3WO(Q),因此,整个改进的萤火虫算法的计算时间复杂度

基本萤火虫算法需要更新萤火虫的最大荧光亮度和位置,同样需要计算适应度值及保留最优个体,其计算时间复杂度

由式(20)可以得到,算法的计算时间复杂度仅与求解问题的问题规模D,种群规模Q 和迭代次数W 有关。对比式(21)可以得到,相对于基本萤火虫算法,改进的萤火虫算法并没有明显地增加算法的计算时间复杂度。
3 TFT−LCD 单元装配调度问题求解
3.1 编码设计与解码过程
萤火虫算法主要用于解决的是连续优化问题,但是,TFT−LCD 单元装配调度这一类混合流水作业车间调度问题属于工件排序问题,即为离散调度问题。根据此类情况,需要建立连续空间到离散空间的映射,本文采用两段式编码[14]和IMM 编码[13]相结合的方式进行编码设计。两段式编码的优点主要是便于解决连续型参数的优化问题。由于两段式编码不能直接用于多机器混合流水调度问题,故运用两者相结合的方式进行编码设计。两段式编码过程如图3 所示。

图3 两段式编码方式Fig.3 Two segments encoding method
如图3 所示,首先设定好每批工件对应的工序和机器。将第二条染色体的工件批数设置为5 批,且每批都有2 个工序,彩色框中的数字表示每批工件每道工序相对应的加工机器。在第一条染色体中,彩色框中的数字为工件加工批数,每个数字出现次数表示工序数。第二行小数是由迭代数据降序排列后得到。如在第二条染色体中,O2在m=2 上加工的为J2,J3,J5,且2,3,5 在第一条染色体中首次出现的顺序为2,5,3,故它们加工的先后顺序也应为J2,J5,J3。m 为机器,J 为工件。所以,第二条染色体是按照第一条染色体设定好的参数并经过迭代后进行降序排序,由此确定加工顺序。为了实现连续型到离散型的映射,随后采用IMM 编码方式,它是基于随机键并借助中间媒介的一种编码方法,其中包含2 个过程:从实数集合xi到工件排序πi的阶段以及从工件排序πi*到实数集合xi*的阶段。先将随机获得的实数集合 xi={xi1, xi2, ···, xin}按降序进行排列,得到了中间集合 ϑi={ϑi1, ϑi2, ···, ϑin},随后依据 πi,ϑij= j 的 准 则,取 得 中 间 介 质 为 ϑi′,最 后 一 步xi'再按照ϑi'选取初始实数集合xi的第j 个数。
在解码过程中,首先将萤火虫的位置转化为一个有序的工作表,随后根据工作表和工艺要求对每个操作以其最早允许加工时间逐个开始加工,最终就会产生目标函数值。
3.2 仿真实验与分析
为了研究TFT−LCD Cell 阶段调度问题,本文根据TFT−LCD 生产企业单元装配的生产情况,结合此次调度问题,设定了产品批量数以及产品种类,其中,工件种类n=3,加工机器m=5,整个加工过程包含11 道工序,表1 为在3 台机器M1,M2,M3上,3 种类型的产品所对应的产品加工时间。例如,O11表示在第一道工序中,类型1 的产品在3 台机器上的加工时间分别为12,11,10。表2 为3 种类型产品所对应的批量数。表3 为各工序所对应的机器数目。表4 为各类产品所对应的交货期及加权延迟。
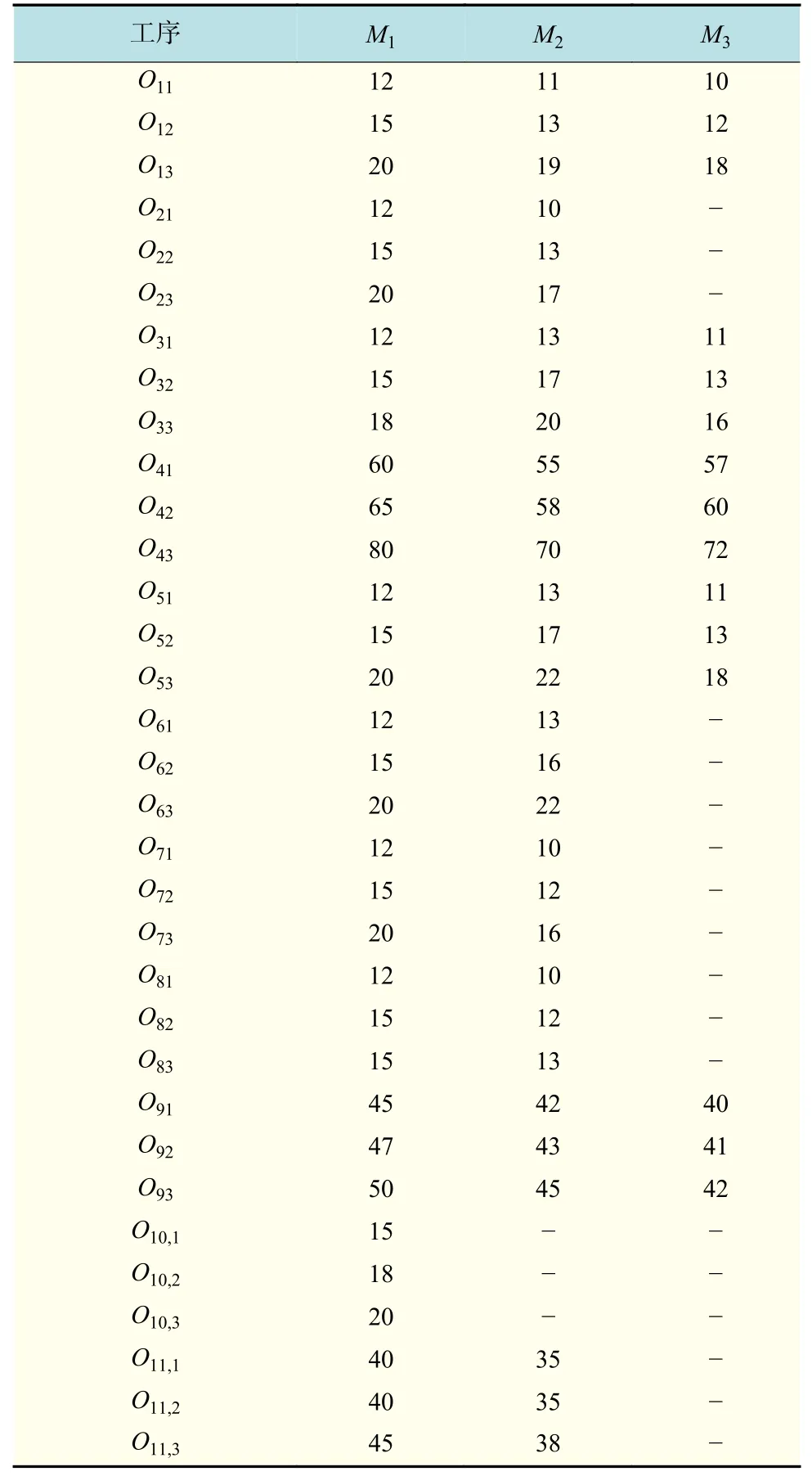
表1 3 台机器产品加工时间表Tab.1 Machine processing time min

表2 产品批量数Tab.2 Work-piece type and lot size

表3 各工序机器数Tab.3 Machine numbers in each process

表4 工件交货期及加权延迟Tab.4 Work-piece basic information
运用萤火虫智能算法求解TFT-LCD 单元装配调度问题仿真实验操作系统为Windows 7,CPU Intel(R)Core(TM)i 5−5200 U 及8 G 内存,采用Matlab R2014a 进行算法编程。采用萤火虫算法参数设置:种群规模为50,迭代次数为100,光强吸收系数为1,随机因子为0.5,算法独立运行10 次。
由表5 可知,在单元装配调度问题中,萤火虫算法(FA)求解得到的最大完成时间优于遗传算法中的贪婪解码(GD)和静态解码−精英保留(SD−ES),而加入混沌搜索机制的萤火虫算法(ICFA)与标准萤火虫算法(FA)相比更加具有优势,图4 为ICFA 算法与FA 算法的结果对比图。
如图4 所示,横坐标表示迭代100 次后,算法独立运行10 次;纵坐标表示最大完工时间。Cmax1表示标准的萤火虫算法,Cmax 表示加入混沌搜索萤火虫算法。Cmax 曲线明显优于Cmax1 曲线,Cmax1 曲线波动幅度较大,而Cmax 曲线趋于平稳状态,说明改进的萤火虫算法(ICFA)结果优于萤火虫算法(FA),并且稳定性较好。

表5 4 种方法得到的最大完工时间Tab.5 Cmax obtained by four methods min
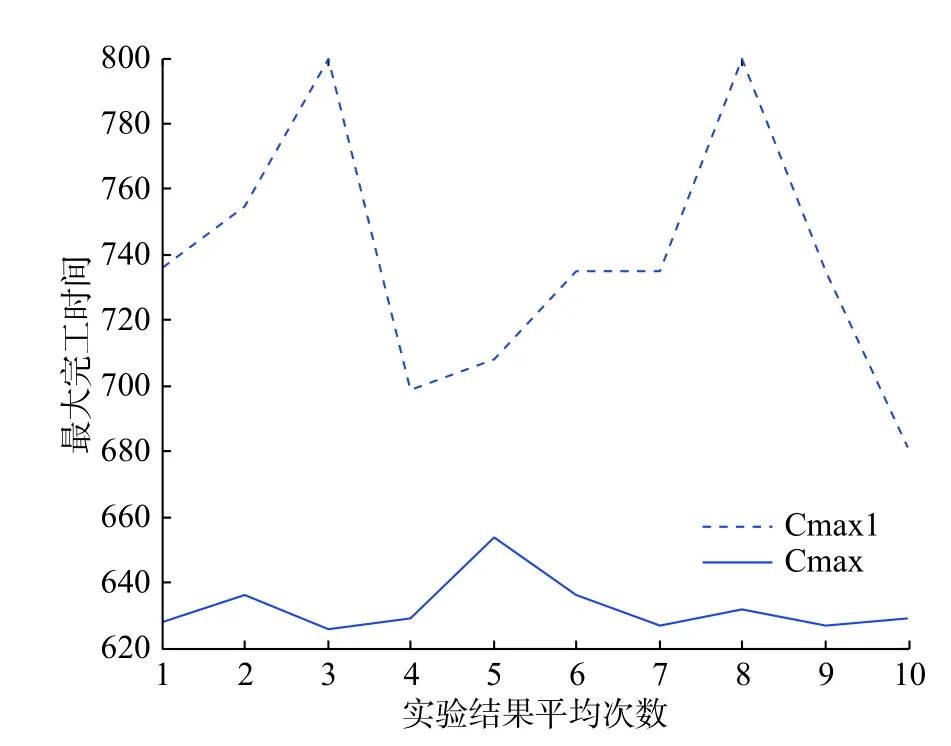
图4 ICFA 和FA 最大完工时间对比Fig.4 Comparison between the Cmaxs of ICFA and FA
表6 为4 种方法得到的目标函数值,从表中可以看出,萤火虫算法(FA)要优于遗传算法中的贪婪解码(GD)以及静态解码−精英保留(SD−ES)。另外,加入混沌搜索后的萤火虫算法的结果优于标 准的萤火虫算法。

表6 4 种方法得到的目标函数最优值Tab.6 Objective function obtained by four methods
图5 为加入混沌搜索后的萤火虫算法(ICFA)与标准的萤火虫算法(FA)目标函数值的对比图,从图中可以看出,改进后的萤火虫算法结果(Obj1)明显 优于标准萤火虫算法(Obj),且结果的稳定性更好。

图5 ICFA 和FA 算法目标函数最优值对比Fig.5 Comparison between the optimal ralues of objective functions of ICFA and FA
综上所述,同一实验数据,加入混沌搜索后的萤火虫算法在求解最大完工时间以及目标函数值时,其结果都要优于标准的萤火虫算法的求解结果。从运行结果比较得出,改进后的萤火虫算法的解最优,能取得最短的完工时间,从而可以保证工件能够按时交货。
4 TFT−LCD Cell 阶段调度问题模型
4.1 学习效应对TFT−LCD 单元装配阶段影响分析
学习效应是1936 年美国康奈尔大学的Wright[15]在研究飞机制造过程中劳动时间与产量之间的规律时发现的,并首次在制造业中提出经验曲线。Yelle[16]在1979 年第一次采用另一个名称——学习曲线来定义经验曲线,最初的学习曲线的表达式为

式中:Y 为第x 个零件的加工时间;X 为累积加工量;T1为第一个工件的加工时间;a 为学习因子,a<0。
学习曲线如图6 所示。

图6 学习曲线Fig.6 Learning curve
在经典的生产调度问题中,每个工件每一道工序的加工时间都是固定不变的,并不会考虑到工件加工时间会受到所在加工位置的影响。然而在实际生产中,由于工人会从前一个工件的加工生产中吸取经验,后一个加工工件会比前一个工件所需加工时间要少,这就是学习效应。但是,在实际的加工生产中,机器不可能一直保持高强度运转状态,当下一台机器准备要加工的工件还在上一台机器加工时,就会产生空闲时间,并且还存在设备设置时间以及工件类型的改变这些影响加工时间的因素,这就有了遗忘效应。Biskup[7]是第一位将学习效应应用于排序问题的学者,他指出,由于工人不断地重复类似的加工工作,其熟练程度会越来越好,所以,后一个工件所需的加工时间就会比前一个工件加工时间少,加工时间与工件排序中其加工的位置相互之间为递减的函数关系。
综上所述,在生产作业车间中,学习因子和遗忘效应与工件加工位置和工件等待时间有关,本文在借鉴文献[17]的学习效应模型的基础上,建立了针对混合流水车间的学习遗忘效应模型。

4.2 学习遗忘效应对TFT−LCD 单元装配调度问题的影响
在TFT−LCD 单元装配调度问题中,学习效应和遗忘效应是共存的,由于加工机器的不同,学习率和遗忘率也会有所不同。当学习率l 分别取0.7,0.8,0.9,1 时,与之相对应的学习因子a 就取−0.515,−0.322,−0.152,0,遗忘率b 分别取0.1,0.2,0.3。
本文采用改进的萤火虫算法独立运行20 次,各算例随机生成50 组数据,计算TFT−LCD 单元装配阶段调度问题在相同学习率、不同遗忘率的所有情况。从图6 中可见,随着学习率与遗忘率的变化,最大完工时间也随之变化,说明学习遗忘效应会影响最大完工时间。
在TFT−LCD Cell 阶段调度过程中,遗忘效应和学习效应是共同存在的,所以,如果去单一考虑其中一个效应,就会造成实验结果不准确,导致资源没有进行合理的分配,从而影响了整个调度结果。图7 中黑线、红线、绿线表示在遗忘率b 分别为0.1,0.2,0.3 时,学习率分别为1,0.9,0.8,0.7 时对应的目标函数曲线,学习率1,0.9,0.8, 0.7 分 别 对 应 的 学 习 因 子 为0, −0.152,−0.322,−0.515。从图中能够明显看出,3 条曲线的趋势存在明显差异,遗忘率越大,目标函数值越大,目标函数随着遗忘率的增加而增加,两者成正比关系,遗忘效应的增加表明工件的等待时间会对最大完工时间产生较大的影响,这是符合实际情况的。同时可以发现,当学习率较高时,最小化最大完工时间也随之增大,在学习率l∈(0.7,0.8)时,即学习因子在(−0.515,−0.332)区间时,曲线呈现明显的上升趋势,即目标函数上升趋势明显,这表明在加工生产中,有可能短时间内大量设备出现故障使得生产中断或者产品种类的变更等其他影响加工生产进度的状况出现,都会导致工期延长。当学习率越低,遗忘率的影响也就越小,这时最大完工时间也就越小。当学习率大于0.8 时,曲线渐渐趋于平滑,表明随着学习效果的持续下降,最大完工时间并不会呈直线型增长,而是慢慢地趋于一个稳定值。

图7 具有不同学习率和遗忘率的目标函数变化趋势Fig.7 Objective function curves with different learning and forgetting rates
5 结束语
对TFT−LCD 单元装配阶段作业车间调度问题建立以最小化最大完工时间和加权延迟最小为目标的数学模型,在对传统调度问题研究的基础上,考虑到在实际的机器运行加工生产中,与理想存在较大的差距,引入学习效应和遗忘效应。同时讨论了学习遗忘效应对完工时间的影响,利用加入混沌搜索后的萤火虫算法对模型进行求解,通过与标准的萤火虫算法比较,证明了改进的萤火虫算法在解决TFT−LCD Cell 阶段调度问题时的有效性,具有良好的发展前景。本文的目标函数针对性地考虑了加权延迟以及最大完工时间,在TFT−LCD 生产调度未来的研究中,考虑的问题也必须更加全面,在算法改进方面未来也会尝试更多的改进方法,以期更好地解决在实际生产中存在的问题,进一步提高生产效率,减少机器空闲时间。

