具有可替换能源的智能电网实时电价研究

赵 琳，高 岩

（上海理工大学 管理学院，上海 200093）

能源和环境是当今世界两大热门话题，在科技发展和环境需求的共同驱动下，能源结构向更安全、更高效、更低碳的方向转型。电作为一种清洁能源，以其安全、高效、可持续的优点，占据能源市场的半壁江山。然而，传统火力发电所产生的温室效应气体对环境造成的负担日益加重，故国家限制火电的发展，鼓励使用其他清洁能源。因此，以风能和太阳能为代表的新能源，以及家居用户的分布式发电设备集中或分布接入电网，其对传统电网的安全性与稳定性的要求也愈来愈高，由此国家提出建设智能电网的方案[1-3]。

1 研究背景

电力产品有多种定价方式，主要包括固定电价、分时电价、阶梯电价、关键峰荷电价、自适应电价和实时电价。良好的电价机制是根据电网的运行状态和用户自身的用电需求，灵活地调整用电时间和用电数量，从而减少用户的支出。从社会角度来看，良好的电价机制可以有效缓解电力供需不平衡等问题，从而增加社会综合效益。在各种定价机制中，最理想电价机制应是实时电价。

在智能电网中，智能电表不仅能够实时提供用户能源使用情况、电价计费等相关信息，还具有双向通信、远程调控等能力，它是实施实时电价机制过程中的硬件保证。利用高速双向交流、信息、控制技术[4-9]，可以实现智能电网中多种电价计费方式、远程控制供断电、用户互动等功能。

智能电网环境下，除了智能电表，智能用电设备也是先进测量设备体系中的重要组成部分，未来智能用电设备主要包括智能插座、智能家电等。通过智能用电设备，智能电网能更好地实现供电侧和需求侧的信息互动。

近年来，电器分类是智能电网中一个非常值得研究的问题。目前，国内外已有许多关于智能电网电器分类的研究。文献[10]主要对可控电器进行分类，将其分为空调类电器和热水器类电器，并以用户为中心，提出了两种算法进行仿真，其优点是能够较好地平衡用户舒适度和价格喜好。文献[11]将电器类型分为不可转移类电器（指不具备调节能力的电器，用户对其使用为硬性需求，如电冰箱、安保系统）、可控电器（指具备调节能力的电器，如台灯、空调）、可转移类电器（指固定时间内消耗电能的电器，如洗碗机、电动汽车）。针对可转移类电器和可控电器，根据它们的负载模型，提出一个基于多元线性回归的学习模型，旨在学习客户的消费模式。文献[12]在文献[11]的基础上，根据不同类型用电设备的用电特征，制定用电战略及建立用电建模；当价格浮动时，能源分配调度器按优先级将电能分配给用电设备工作，从而满足更多的用电设备工作需求。然而，目前还未有文献将电器分为通用电器和使用替代能源电器。

本文将电器分为通用电器和使用替代能源电器，基于社会福利最大化模型，改进其算法，通过智能电表实时获取信息，比较电价与其他能源价格，能源分配调度器根据比对结果智能地调整能源使用方式，从而使用户社会福利最大化。

2 社会福利最大化模型

智能电网中，将用户预期的用电时间分为 k个时隙， k∈K ，K为所有时隙的集合。将所有用户的集合表示为n，n∈N ，每个用户i∈N。对每个用户i∈N和每个时 隙k∈K的能耗区间，定义为，∈[,]。表示用户i在 时隙 k内的耗电量，耗电量必须满足，和分别表示用户i在 时隙 k内最小耗电量和最大耗电量。最小耗电量为日常生活无法中断的电器所消耗的电量，如冰箱等；最大耗电量为假定所有电器都处于使用状态时所消耗的电量。

为满足日常生活、工作和生产所需，电力供应商应至少保证所有用户在时隙 k内的最小用电需求，即：

2.1 社会福利最大化模型描述

考虑在同一电力供应商下，将用户总效用与电力供应商的成本差最大化，效用函数之和减去电力供应商成本后的结果作为目标函数[13]，建立公式（1）所示优化问题，并分析该问题解的存在性和唯一性。在下面的系统模型中，电力供应商基于总负载需求来发布实时电价。

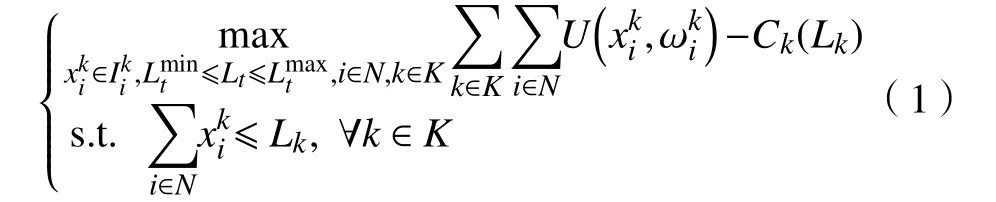
式中：效用函数 U (x,ω)表示用户用电量所获得的满意程度， x为用户的耗电量水平， ω为用户喜好的一个参数变量，用来区分不同用户； Ck(Lk)为时隙k电力供应商的供电成本。在优化问题（1）中目标函数为全社会总福利，约束条件为全部用户用电量不超过总发电量，因此其含义为现有的总发电能力下，如何用电使全社会效益最大化，故被称为社会福利最大化模型。由于优化问题（1）在每个时段都是独立的，因此可将公式（1）转化为如下等价优化问题，求得时段 K内的最大社会福利为

此外，社会福利最大化模型在各个时段上不具有耦合性，可对每个时段分解计算，本质上是分布式方法。

效用函数 U (x,ω)满足以下性质：

a.用户的效用函数为非递减函数，即边际效用∂U(x,ω)/∂x 0，用 ν (x,ω)来表示，含义为用户总是希望使用更多的电量来满足自身的最大消耗水平；

b.用户的边际效用函数为非递增函数，即有∂V(x,ω)/∂x 0，即效用函数是凹函数；

c.智能电网中，不存在用户时，电力就不存在消耗，同时也不存在用户效益，即∀ ω>0 ， U(0,ω)=0，且∂ U(x,ω)/∂ω>0。

通常选取二次效用函数，表示为

式中，α为预先设定的参数。

电价成本函数一般要求满足如下假设[10]：

a.在电力供应商供电能力范围内，其成本函数是递增的；

b.成本函数是凸函数。

电力供应商的供电成本函数普遍使用二次函数：

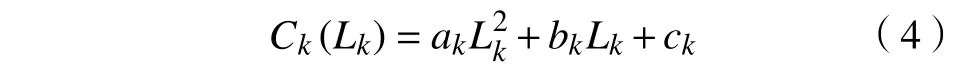
式中，ak，bk，ck均为常数，且ak0，bk0 ，ck0。

效用函数中ω是用户喜好的一个参数变量，为用户隐私参数，电力供应商无法获取该参数。故在求解实时电价时，不直接求解社会福利最大化问题，而是依据它来确定电量的影子价格，即求它的拉格朗日乘子[13-16]，所得到的价格可用于政府制定电价或制定指导价格。影子价格又称“最优价格”、“计算价格”、“预测价格”，是反映社会资源获得最佳配置的一种价格。

2.2 求解方法

对偶方法起源于线性规划，后逐渐发展成为求解一般非线性优化问题的方法，是最优化理论中一个重要求解方法。对偶方法不仅可以求解优化问题的决策变量，同时还可以附带求解拉格朗日乘子。因此，一般采用对偶方法对社会福利最大化实时电价优化模型进行求解。另外，社会福利最大化模型在各个时段上不具有耦合性，算法可对每个时段分解计算，其本质为分布式方法。

问题（2）是一个约束最优化，可以使用拉格朗日乘子法对其进行求解。首先，对问题（2）中每一个固定的时隙k，依据拉格朗日乘子法将约束最优化问题转化为式（5）的无约束最优化问题：

式中， λk为拉格朗日乘子，为 k时隙的实时电价。对于时隙 k ∈K，可以将式（2）中的系统模型转化为

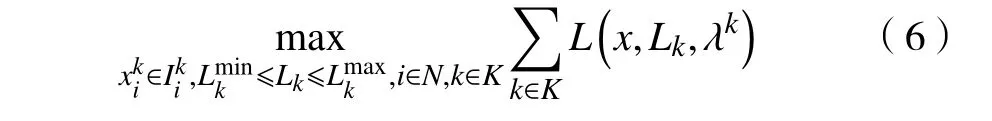
式中，对于每个固定时隙k ，L(x,Lk,λk)为用户在时隙 k的拉格朗日乘子。将式（6）进行整理，得到式（2）的一个对偶问题，其目标函数为

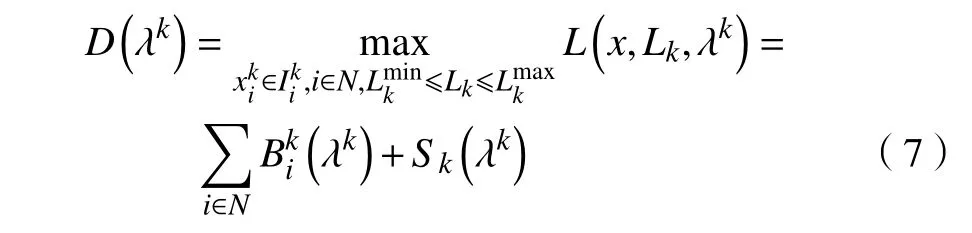
其中

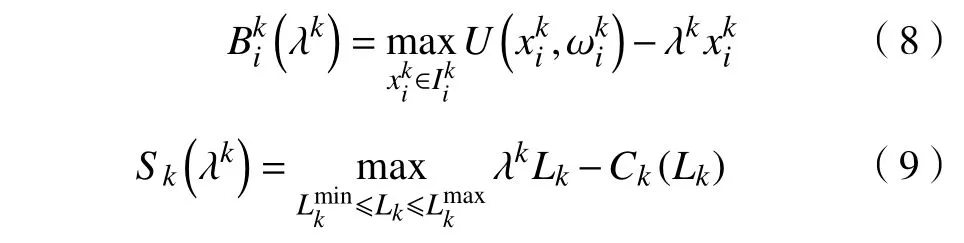
将D(λk)=maxL(x,Lk,λk)对偶问题的核心部分L(x,Lk,λk)划分为两个子问题(λk)和Sk(λk)。其中：问题(λk)与电价和用电量相关，电力供应端计算出实时参考电价，用户端根据电力供应端提供的参考电价，计算出用户的拟用电量；问题Sk(λk)与电价和生产电量相关，电力供应端基于参考电价计算出相应的生产电量（生产电量应满足所有用户的用电量），电力供应端基于求得的最佳生产电量以及所有用户的拟用电量信息对电价迭代修正。

文献[13]中，给出了一种分布式算法——对偶分解法，对于式（7），其对偶问题为

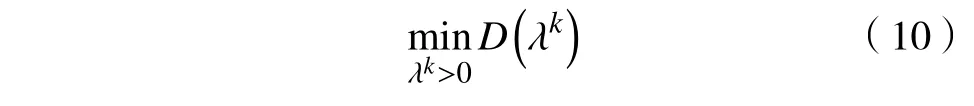
为解决该对偶问题，采用梯度投影迭代法进行求解。在一般情况下有以下迭代公式[15]：

式中：t ∈T为时隙k内电力供应商更新λk的一个时间序列集； λk为在t ∈T时隙的值，其 中(),Lk∗()为 式（8），（9）中关于的局部最优值； γ为步长。经过迭代后，电力供应端将新的电价继续传送给用户端，用户在确定它们新的拟用电量后重复这个过程，直到电价不变或变化微小，这一过程体现了用户端和电力供应商之间的互动。

3 具有可替代能源的社会福利最大化模型

随着电力市场以及科技的发展，目前我国正处于多种能源设备的起步阶段，人们生活水平越来越高，混合动力汽车开始纷纷进入市场，住宅小区也开始普及地暖设备（天然气地暖/电地暖）。在如今多种能源可切换使用的情况下，用户可以通过改变智能用电设备的能源使用方式，使得自身福利最大化。

一般情况下，用户总是趋向于自己福利最大的能源使用方式。对于不同的电价水平，不同的用户会有不同的反应。当实时电价超过用户使用其他替代能源的价格时，用户会选择使用替换能源，而停止用电。对于一些必须使用电力资源的用户来说，实时电价对其影响是微乎其微的。例如，用户在早上8 点以后想要使用具有替换能源的设备，那么就会选择使用其他能源来维持设备工作，使得用户福利最大化，如图1 所示。

本文将电器分为通用电器和使用替代能源电器，通过实时比较电价与其他能源价格，能源分配调度器智能地选择能源使用方式。

3.1 系统模型

为了模型简便，作如下假设：

a.能量换算。用户在使用不同能源方式时，每单位电所释放的电能相当于 β单位的其他能源所释放的能量，能源的种类不同，系数 β也随之变化（因此在实际生活中，需要根据实际操作情况，进行能量等值换算）。

b.电器分类。将接入[电网的所有]用[户的集合表]示为n，n∈N ，其中，i=g1,g2,···,gj∪a1,a2,···,aq∈N ；表 示用户 gj在时隙 k内使用通用电器的耗电量；表 示用户ai在时隙 k内使用可替换能源电器的耗电量；用户 gj与用户的 ai总集合为所有用户。

图1 智能对比选择用电方式Fig.1 Comparing and choosing the way of energy using for electrical appliances

c.多种能源价格： p表示替代能源的价格（短时期内通常固定不变）；表示由智能电表实时提供的电价。

从用户福利的角度来看，只有当实时电价超过其他能源价格，用户才会根据价格信号作出相应反应，并调整自己的用电模式。根据以上假设，仍使用式（2）中的社会福利最大化函数，建立如下模型：

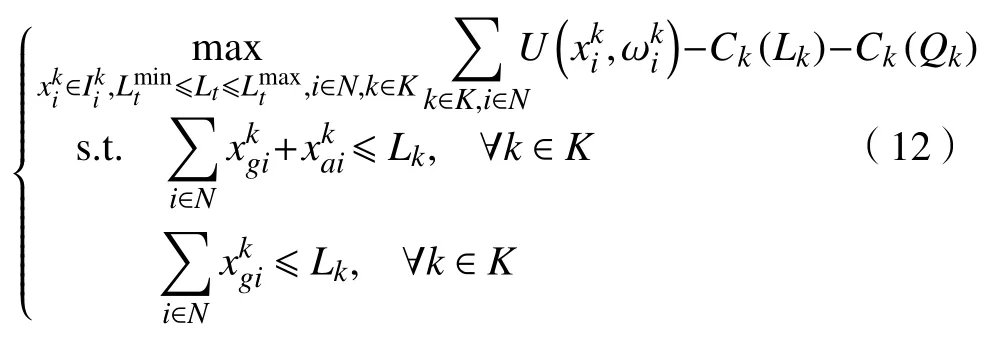
其中效用函数为

成本函数为Ck(Lk)，公式为式（4），Ck(Qk)=（计算结果为常数）。式（12）中表示{ k时}隙的实时电价， p表示其他能源的价格，min,p表示对两种价格进行实时比较。当 m in{,p}=时，电价低于其他能源价格，此时所有用户使用电能，用户的社会福利最大；当 min{,p}=p时，电价高于其他能源价格，通用电器可使用电能，也可使用替换能源电器使用其他能源，此时，用户的社会福利最大。

3.2 模型的求解方法

式中， λk， νk分 别为用户在时隙 k的拉格朗日乘子。将其进行整理，得到原问题的一个对偶问题的目标函数为

其中

其对偶问题为

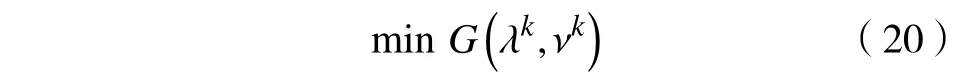
为解决对偶问题，采用梯度投影迭代法对式（20）求解，得到以下迭代公式：

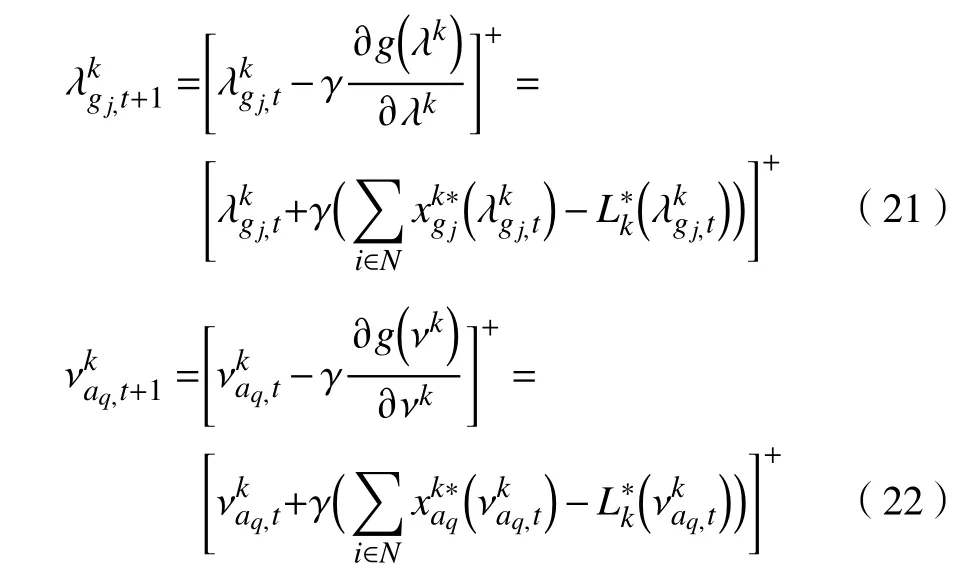
对偶函数分别为

其迭代公式如下：

式中：t∈T,T为时隙k内电力供应商更新拉格朗乘子λk,νk,σk的一个时间序列集，σk在 t ∈T 时 的 值；为式（21），（22），（25）中关于的局部最优值； γ为步长。

3.3 算法步骤

算法1 和算法2 是基于用户端和电力供应端同步进行的分布式迭代算法。算法中简化了市场的复杂性，模糊了实际生活中不同类型的使用条件。通过智能电表，用户和电力供电商之间进行实时信息互动。电力供应端根据所获得的实时信息，对电价和替代能源的价格进行实时比较，通过计算为用户提供最优的能源使用方式，从而使得用户福利最大化。以下为两个算法的实施步骤。

a.算法1（用户端）。

Step 1初始化；

Step 2如果 t ∈T ，接收新的电价：

（a）更新用户耗电量；

Step 3结束。

b.算法2（电力供应端）。

Step 1初始化；

Step 2重复；

Step 3如果 t ∈T，则

（b） 将新的电价与替换能源价格相比较:

Step 4另外:

（a） 更新供应量 Lk∗;

（c） 相应的更新总负载;

Step 5结束。

算法1 中：每个用户以随机的初始状态从Step 1 开始；Step 2，3 为用户对新电价的反馈；Step 2(a)中，将用户接收到的新电价代入，求得其最优耗电量；Step 2(b)中，用户通过智能电表将最优耗电量更新传送给电力供应端。

算法2 中：电力供应端以随机的初始状态从Step1 开始；在系统操作周期中，Step 2～5 不断循环；Step 3 中，在 t ∈T的每个时间序列中，电能供应端将上一时刻的电价与替换能源价格 p相比较。若p，则所有用户使用电能获得福利最大；若>p，则用户可使用替代能源的能源使用方式，电力供应端重新计算得到新电价，调整用户能源使用方式，使得用户福利最大。

4 模拟仿真

在实际应用中，最常见的替代能源为天然气，每立方米天然气燃烧热值为33 494.4～35 587.8 kJ；1 kW·h=3.6×106J =3.6×103kJ,即每立米天然气燃烧热值相当于9.3～9.88 kW·h 所产生的热能，因此，β=9.5。

4.1 参数设置

采用Matlab 对以上步骤进行仿真，有如下假设：

将 N 个用户（ N=5）接入电网中，时隙 k为一天中的24 h，令二次效用函数中参数 αgi,αai=0.25，成 本 函 数 参数 ak=0.01，bk=0 ，ck=0。取 初 始 电价为1，γ=0.01，替换能源天然气的恒定价格 p为2.5，用户参数 ω ∈[1,4]随机取值。

4.2 结果分析

图2 和图3 分别为未使用可替换能源的电价更新和使用可替换能源后的电价更新。由图可以明显看出：当电价超过2.5（替换能源价格）时，可使用替换能源电器，不再使用电能，使得用户福利最大化；当电价低于2.5 时，所有电器使用电能，使得用户福利最大化。因此，使用可替换能源电器时电价较低，灵活地调整用电方式，不仅能够提高能源利用效率，同时还降低了用户的电费支出。

图2 未使用可替换性能源电价Fig.2 Electricity price when not using alternative energy

图3 使用可替换性能源电价Fig.3 Electricity price when using alternative energy

图4 和图5 分别为未使用可替换能源的总效用更新和使用可替换能源的总效用更新。由图可知：使用可替换能源比未使用之前的总效用起伏较小，起伏较为平缓，结合图2 和图3 可知，当电价超过2.5（替换能源价格）时，可使用替换能源电器，不再使用电能，而使用其他能源，其总效用也相对减小，但用户获得最大福利。因此，使用具有可替换能源的定价方式，能够灵活地调整用电 方式，实现减少用户支出和社会总效用最大化。

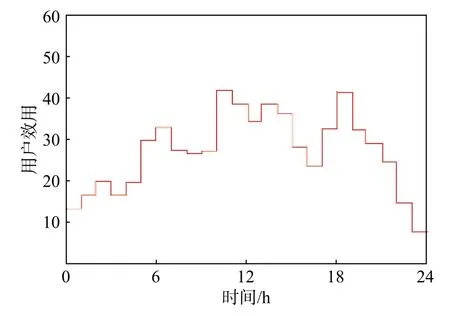
图4 未使用可替换性能源的总效用Fig.4 Total utility when not using alternative energy

图5 使用可替换性能源的总效用Fig.5 Total utility when using alternative energy

图6 和图7 分别为未使用可替换能源的用电量更新和使用可替换能源的用电量更新。图7 相较于图6 可以得出：用户整体用电量波动较小，当电价超过2.5（替换能源价格）时，用户用电量相对减少，因此，具有可替换能源的智能电网可以有效缓解电力供需不平衡，降低系统高峰时段的柔性负荷量，实现削峰填谷，提高电力资源的利用效 率。

图6 未使用可替换性能源的用电量Fig.6 Electricity consumption when not using alternative energy

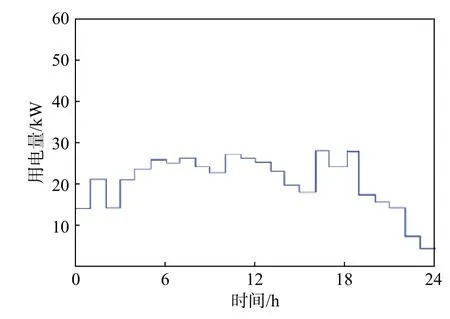
图7 使用可替换性能源的用电量Fig.7 Electricity consumption when not using alternative energy

5 结束语

本文阐述了智能电网中，具有可替换能源的智能电网实时电价。以用户福利最大为目标，设计出一种实时电价模型和算法。电力供应端不断地进行实时判断，比较电价和替代能源的价格，选择最优能源方式，使用户福利最大化。数值模拟结果表明，具有可替换能源的智能电网具有平衡供需、提高用户福利和社会总福利、提高电网稳定性、促进社会资源合理利用等优点。