猴子岩水电站面板堆石坝三维渗流计算分析

张凤财，姜媛媛，窦向贤

(中国电建集团成都勘测设计研究院有限公司，四川 成都 610072)

1 工程概况

猴子岩水电站位于四川省甘孜藏族自治州康定县境内，是大渡河干流梯级开发规划“三库22级”的第9级电站[1]。水库正常蓄水位1 842 m，总库容7.06亿m3，具有季调节性能，电站装机容量1 700 MW。拦河坝为混凝土面板堆石坝，坝顶高程1 848.5 m，最大坝高223.5 m，坝顶总长278.35 m。

该工程拦河坝坝体主要通过混凝土面板、混凝土趾板和面板接缝止水防渗。坝基通过趾板下帷幕灌浆防渗。为防止绕坝渗漏，两岸坝肩设置了帷幕灌浆防渗。两岸趾板建基面大部分置于弱风化上段强卸荷岩体上，河床段趾板基础坐落在回填混凝土上。两岸趾板采用“定宽趾板+防渗板”，在两岸趾板下游的基岩面20 m范围内采取网喷混凝土及固结灌浆等措施以延长渗径，喷混凝土后面适当范围岩面铺设反滤层以控制渗流。坝前1 735 m高程以下为压重区，面板等防渗结构不具备检修条件，且该范围面板承担的水压力相对较大，一旦面板出现开裂等状况，将导致大坝渗漏量增加，影响工程经济效益，甚至危及工程安全，因此在压重区范围面板前铺填石粉，面板开裂后石粉可迅速充填裂缝，使其自愈。

2 渗流计算方法及边界条件

本文计算采用饱和稳定渗流有限元方法[2]，基本微分方程为

(1)

式中，xi，xj为坐标，i，j=1，2，3；kij为达西渗透系数张量，当i=j时，kij=k，当i≠j时，kij=0；h为总水头,h=x3+p/γw,其中x3为位置水头，p/γw为压力水头。

微分方程的定解边界条件：

H|Γ1=h1

(2)

(3)

(4)

(5)

式中，h1为已知水头函数；ni为渗流边界面外法线方向余弦，i=1,2,3；Γ1为第一类渗流边界条件，即定水头边界条件；Γ2为第二类渗流边界条件，即流速边界条件；Γ3为渗流自由面；Γ4为渗流逸出面；vn为法向流速。

在求得渗流场有限元数值解(各单元结点水头值)后，可采用插值网格法计算任意四边形断面的渗流量。待求渗流量的任意四边形断面记为S1，面积为A，假设其沿法线方向偏移距离L得面S2，点1、点2分别为面S1、S2的形心，h1、h2分别为点1、点2处的总水头，见图1。当偏移距离L相对于截面积A足够小，即L趋于0时，根据达西定律，通过断面S1的渗流量可近似为

(6)

式中，kn为法向渗透系数。

将四边形断面S1、S2按同样的规则离散成细密的网格单元，则通过断面S1的渗流量计算公式可改写为

(7)

式中，n为离散后的网格单元总数；kni为单元的法向渗透系数；Ai为单元的面积；Δhi为每对离散网格单元形心处的总水头差。

假设某个离散单元的形心为点A，同时假定已计算出节点水头的单元为空间八结点六面体等参数单元，点A在该六面体单元中(见图2)，则点A的总水头为

(8)

式中，hi为六面体单元8个结点的水头值；xi(ζ,η,ζ)为用局部坐标表示的单元形函数。根据上式求出每个离散网格单元形心处的总水头，进而可求出通过任意四边形断面的渗流量。

图2 八节点六面体等参数单元示意

3 计算参数、模型及工况

3.1 计算参数

表1为根据试验结果以及工程经验类比确定的各主要材料渗透系数。

表1 各主要材料的渗透系数计算取值

3.2 计算模型

将面板、趾板、帷幕及垫层等主要结构进行精细化建模，其余渗透特性相近的材料适当合并简化，模型中裂缝均采用薄实体单元模拟。

计算模型底部高程为1 345 m，位于较深的基岩内，取为隔水边界；由于水库蓄水后，天然地下水对渗流场的影响较小，两岸山体边界取为隔水边界；上游水位取正常蓄水位1 842 m，正常蓄水位以上部分取为隔水边界；下游水位取一台机组发电时的水位1 695 m，下游水位以上地表取为可能自由逸出边界。

图4 正常工况下大坝渗流场分布(单位：m)

3.3 计算工况

本文取6种工况进行计算，分别为：①工况1，正常蓄水位稳定渗流工况；②工况2，假设面板在高程1 770 m处出现一条横向水平裂缝(h1)，缝长约为95 m，缝宽为3 mm；③工况3，假设面板在0+163.8 m、高程1 760～1 818 m范围出现一条纵向垂直裂缝(z1)，缝长约为128 m，缝宽为3 mm；④工况4，假设面板在0+201.5、0+163.8、0+128.7 m，高程1 760～1 818 m范围内分别出现3条纵向垂直裂缝(z2、z1、z3)，缝宽均为3 mm；⑤工况5，假设面板出现纵向垂直裂缝z1，垫层料渗透系数取5.5×10-7m/s；⑥工况6，假设面板出现纵向垂直裂缝z1，垫层料渗透系数取5.5×10-5m/s。

图3给出了本文计算假设的面板横向水平裂缝和纵向垂直裂缝位置。

图3 计算所假设的面板裂缝位置

4 分析成果

4.1 正常工况分析

图4为正常蓄水位稳定渗流工况三维计算所得大坝河床中部的浸润线和等水头线分布，从图4中可以看出，等势线分布符合一般规律。由于面板、趾板、趾板基础帷幕及坝肩帷幕的联合防渗作用，河谷部位水位降落达137.13 m，即河谷段垂直防渗系统削减了93%以上的水头，左、右岸山体基岩防渗帷幕的防渗效果明显，幕前高水头经过山体帷幕后明显折减。通过面板及趾板的渗漏量为3.05 L/s，通过趾板下防渗帷幕和地基的渗漏量为219.38 L/s，两岸帷幕及山体的绕渗量为66.58 L/s，大坝下游量水堰的渗漏量计算值为203.54 L/s。整个防渗体系承受了较大的水力坡降，其中，面板的最大水力坡降达175.00，防渗帷幕的最大水力坡降达24.01，面板下游侧的垫层料水力坡降较小，最大值为0.60，坝体堆石料渗透系数较大，等水头线稀疏，水力坡降较小，坝基各覆盖层的水力坡降均未超过允许水力坡降。分析成果表明，设计防渗方案满足渗流与渗透稳定性要求。

与水库实际运行情况对比发现，堆石区水位的计算值和监测成果基本吻合，说明防渗系统的施工质量较好；计算过程中由于将裂隙岩体按等效连续各向同性介质来进行处理，因此量水堰的渗漏量计算值(203.54 L/s)比实测值(176.73 L/s)偏大；三维渗流计算成果表明，大坝下游的渗水主要来源于坝基及坝肩绕渗，面板渗水很小，现场水样水质简分析结果也反映了这个规律，证明目前面板性态良好。

4.2 面板开裂对渗流场的影响

各工况关键部位的水力坡降、相对水位变化及通过面板渗水量见表2。假设面板产生裂缝后，裂缝下游侧一定范围均会形成一个饱和区，纵向垂直裂缝对应饱和区范围要大于横向水平裂缝；堆石区水位会有不同程度抬高，且水位影响区会向下游及左右岸延伸相当长的距离，单条纵向垂直裂缝引起的水位抬高幅度小于单条横向水平裂缝，但当面板同时出现多条纵向垂直裂缝时，堆石区水位则会大大抬高；垫层料的水力坡降会较面板没裂缝情况大大提高；完好的混凝土面板几乎是不透水的，当面板出现横向水平裂缝后，通过面板的渗水量会大大增加，出现纵向垂直裂缝后，通过面板的渗水量增加会更严重。可见，面板出现裂缝后，会严重影响工程的蓄水效率，甚至危及工程安全，如何采取妥善可靠的措施尽量避免面板开裂是混凝土面板堆石坝设计和施工质量控制的重点之一。

4.3 垫层料渗透特性对渗流场的影响

本文以面板出现纵向垂直裂缝z1为例，研究垫层料渗透特性对渗流场的影响。各工况关键部位的水力坡降、相对水位变化及通过面板渗水量见表2。当假设垫层料的渗透系数缩小10倍，取5.5×10-7m/s时，相对面板没出现裂缝的情况，堆石区水位仅抬高0.74 m，远小于工况3的水位抬高值，且此时裂缝下游侧饱和区范围很小；当假设垫层料的渗透系数放大10倍，取5.5×10-5m/s时，相对面板没出现裂缝的情况，堆石区水位抬高4.40 m，大于工况3的水位抬高值，且此时裂缝下游侧产生了一个很大的饱和区；此外，其余条件一样的情况下，当垫层料渗透特系数变化时，除垫层本身的水力坡降会发生变化外，帷幕水力坡降及通过面板的渗水量也会随之发生一定程度的变化。

因此，垫层区是混凝土面板堆石坝的关键部位之一，要进行精细设计，施工过程中应严格控制垫层料的料源及碾压质量，并对其采取可靠的反滤保护措施，避免面板开裂时垫层料发生渗透破坏，进而威胁大坝安全。

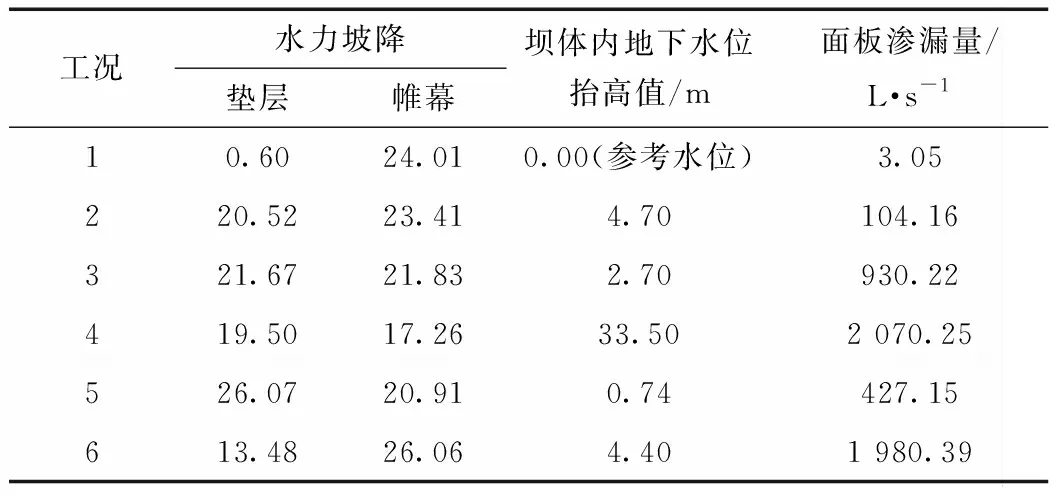
表2 各工况坡降、水位、渗漏量

5 结 论

本文对猴子岩水电站混凝土面板堆石坝的正常工况和假设面板出现不同型式的裂缝等非常工况，分别进行了三维渗流稳定分析，并以一条纵向垂直裂缝为例，研究了垫层料渗透特性对渗流场的影响，基于计算成果可得到以下几点初步结论：

(1)从正常工况分析的渗流场、关键部位水力坡降、堆石区水位、渗漏量等成果可知，该工程的防渗系统设计是合理可靠的，满足工程蓄水效率、渗透稳定及坝坡稳定等要求；大坝运行的监测成果与计算成果较为吻合，说明防渗系统的施工质量较好，目前面板性态良好。

(2)完好的混凝土面板几乎是不透水的，当面板局部发生水平或竖向裂缝时，裂缝附近的垫层区中会出现集中的水头损失和较大的渗透坡降，堆石区水位抬高，坝体渗漏量增加，会严重影响工程的蓄水效率，甚至危及工程安全。如何采取妥善可靠的措施尽量避免面板开裂是混凝土面板堆石坝设计和施工质量控制的重点之一。

(3)若混凝土面板出现裂缝，坝区渗流场及渗流量受垫层渗透系数的影响较大，应特别注意垫层的料源及填筑碾压质量。