基于灰色关联算法的军事运输路径优化

阮 博，郭 平，雷 晏，张志峰

(1.陆军勤务学院 军事物流系，重庆 401311； 2.陆军勤务学院 勤务保障实验中心，重庆 401311； 3.陆军勤务学院 网管中心，重庆 401311)

军事运输是军队机动的基础，更是后勤保障的中心环节和影响战争胜负的关键因素。公路网是军事运输网络的重要组成部分，在军队人员和装备的输送中起到了至关重要的作用。在运输过程中，对公路网的部分路段实施交通管制，是保障运输任务顺利完成的一种特殊手段，是落实保密防间要求的一项有效措施。平时条件下部队遂行演练、驻训及转场等任务在区域公路网中选择运输路径时，应在确保运输任务完成的基础上兼顾时效性、经济性及低影响性等因素，合理选择有效路径，并根据任务需要决定是否对部分路段进行管制。然而，如何筛选确保军队运输任务完成的有效路径并从有效路径中确定最优运输路径，且评估最优路径对公路网的影响程度，这些都是亟需研究的课题。

路径对路网的影响程度属于路径重要性的研究范畴。当前，对路径重要性的研究少见，而集中于路段重要性的研究。王伟[1]建立了城市路网的路段失效影响评估模型，并将路段的失效概率与失效后对路网的影响程度的乘积作为路段重要性指标。黄大荣[2]等人基于复杂网络理论，设立各条路段对于攻击的脆弱性指标，评估路段重要性。这些研究对于评估路段重要性具有一定的理论参考作用，对由路段构成的运输路径的重要性研究也有一定的启发借鉴作用，但该研究集中于城市路网，对区域公路网涉及较少。也有不少学者围绕多目标军事运输路径优化问题展开了研究。臧涛涛[3]采用时间、路径长度、危险性及公路状况4种指标，运用模糊层次分析法，求解战时运输最优路径。姜海洋[4]等人建立运输时间和风险时间权重的可决策路径优化模型，并通过改进的Dijkstra算法，求解最优路径。这些成果的研究背景均集中于战时条件下，大多考虑运输时效性和安全性等指标，极少考虑所选运输路径对民用运输的影响，且忽视了最优路径临时失效时可供通行的备选路径。作者拟建立包含路径影响程度的多目标决策模型，并基于灰色加权关联算法，求解最优运输路径和按优劣排序的备选路径，以期为军事运输过程中的选路提供理论参考，同时，对民用运输的调配起到了一定的启发作用。

1 交通量分配模型

1.1 区域公路网拓扑

目前，许多网络研究成果和复杂网络理论在交通网络研究中得到广泛应用[5-6]。区域公路网属于典型的交通网络，可以抽象成网络拓扑模型。以G(V，E)表示区域公路网拓扑，V={v1，v2，…，vi，…vk}为节点集合，表示交叉口等通行要处；E={e1·2，e2·3，…，ei·k，…，ek·j}为边集合，表示连接通行要处的公路。

1.2 交通管制的时机

运输车队在饱和度较大的路段中受到较大的阻碍，速度减缓、耗费增加。严重时，甚至影响正常通行，导致运输任务延误。为确保运输任务顺利完成，考虑对行进路线上饱和度较大的路段实施交通管制。因此，本研究以饱和度的大小作为是否实施交通管制的依据，设立饱和度阈值μ，对饱和度超过μ的路段实施交通管制。交通管制包含禁行和限行等多种措施。本研究假设实施交通管制后，社会车辆将禁止从管制路段通行。

1.3 交通量分配模型

1.3.1 边介数

介数是复杂网络统计特性之一，用于评价人在社会网络中的重要性指标，是对经过某节点(边)的最短路径数目的统计量[7]。边介数用于区域公路网时表示经过某条边的最短耗时路径数目，能够反映边所对应路段上交通量的大小。

(1)

式中：Bedge(ij)为边eij的边介数；σmn(ij)为节点vm和vn之间最短路径中经过边eij的数目。

1.3.2 路段初始交通量

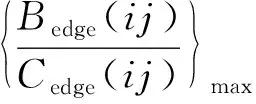
1.3.3 交通量分配策略

当运输车队行进路线上的某一路段饱和度超过阈值时，该路段被实施交通管制，其承载的交通量将会进行重新分配，这个过程类似于网络级联失效中失效节点的负载重分配过程。部分网络级联失效研究[8]中将失效节点的负载分配给相邻节点，该分配策略简单易计算，但与实际情况存在着差异。交通网络中的某一路段实施管制后，其交通量变为0，预先准备经过该路段的出行者将会重新规划路线，寻找新的最短耗时路径，原本由该路段承载的交通量将会分配到其他路段中。因此，管制路段上的交通量应该在全局范围内重新分配，而非在相邻路段上局部分配。

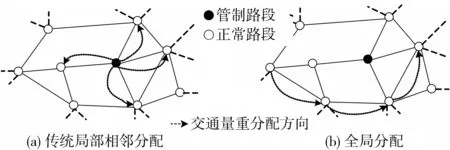
图1 交通量重分配方式的比较Fig.1 Comparison of redistribution methods of traffic volume

假设运输路线上的某一条或几条路段饱和度超过阈值，则在公路网拓扑中将其中第一条删除，该路段的交通量和饱和度均变为0。公路网中各OD对的最短耗时路径将发生变化，由此导致边介数也将发生变化。根据公路网交通总量不变的原则，对各边按照新的边介数比例进行交通量重分配。交通量第一次重分配结束后，观察运输路线上各路段的饱和度是否全部在阈值以下。如果仍存在路段饱和度大于或等于阈值，则再次将其中第一条删除，公路网中剩余路段的交通量将再一次重新分配。重复以上步骤，直到运输上的路段饱和度全部在阈值以下，则运输路线上的所有路段均达到通行要求，公路网中各路段交通量处于稳定状态。

2 有效路径求解

在军事运输起迄点确定的情况下，公路网中的可达路径数量较为庞大。如果从所有可达路径中选择最优路径，需遍历所有可达路径，这一过程将面临巨大的计算量。为提高计算效率，需要从大量可达路径中筛选出数量较少且满足运输任务基本要求的有效路径。

2.1 路径容忍系数

路径长度是判断路径优劣的常用指标，在无区别边的路网问题中经常被使用。公路网中的路径优化属于多目标决策问题，长度虽然不能作为路径优劣评判的直接指标，但长度过大的路径将造成较大的运输时间和运输消耗，这一特性使得长度可以作为界定范围和排除较差路径的指标。因此，本研究设立OD对路径长度阈值，长度在阈值范围内且不存在环路的路径即为有效路径[9]，定义路径容忍系数β[10]，其值的大小可根据军事运输任务的具体情况进行调节，β≥1。

LR=lshortest×β。

(2)

式中：LR为OD对之间的路径容忍长度。

2.2 k次短路径算法

k次短路径是在单源最短路径基础上进行的拓展和延伸，在交通和通信等网络中应用广泛[11]。Dijkstra[12-13]等人提出最短路径的经典算法和k次短路径算法，具有较好的适用性。为搜索所有有效路径，根据军事运输路径的长度限制要求，在Yen的k次短路径算法中加入容忍系数后，得到的算法流程为：

1) 将各节点之间的运输时间作为边权值，使用Dijkstra算法，计算OD对之间的最短路径P1，记录其长度l(P1)与经过的节点，放入最短路径集中，并将P1记作当前路径Pcurrent，令k=1。

2) 从Pcurrent的起始节点vO至终止节点vD的前一节点，依次将其列为偏离节点。

3) 节点vi被列为偏离节点时，将Pcurrent中位于vi之前的所有节点所连的边去除，同时搜索最短路径集中是否存在节点vi。若存在节点vi，则记录该路径中vi和下一节点之间的边，在当前网络中将其去除。使用Dijkstra算法，计算vi到vD之间的最短路径P′，则以vi为偏离节点得到的替代路径即为Pcurrent中vO到vi的路径与P′的“拼接”。随后，将计算过程中被去除的边恢复。

4) 依次计算从vO至vD的前一节点被列为偏离节点时得到的替代路径，比较各条替代路径的长度，长度最小的即为下一次短路径Pk+1，记录其长度l(Pk+1)和经过的节点，判断l(Pk+1)是否大于β×l(P1)。如果是，则运算结束；如果不是，则将Pk+1放入最短路径集中，并记作当前路径。

5) 重复2)～4)，直到运算结束；运算结束时的最短路径集即为所求前k次短路径集。

3 运输路径多目标决策模型及求解

在平时条件下，部队运输受敌打击、袭扰的安全威胁较小，安全风险因素不是运输目标的重点，因此，不予考虑。当面临演练、驻训及转场等任务时，运输车队在公路网中选择行进路径既要考虑时效性，力争在较短的时间内完成运输任务，促进部队战斗力的生成，也要考虑经济性，尽量减少运输途中的消耗，实现低消耗、高效率运输；还要考虑低影响性，在确保任务完成的基础上，降低对社会车辆出行的影响程度，减小对社会经济建设的影响，因此，平时条件下的军事运输选路问题属于多目标决策问题。

3.1 运输时间

快速性、时效性是军事运输的首要特性。在区域公路网中，运输车队经过各条路段的时间可由BPR模型求解。BPR模型由美国联邦公路局提出，是目前交通规划领域使用最为广泛的阻抗函数模型，但由于美国公路与中国公路有所不同，对中国境内的公路使用BPR模型计算时间存在着一定的不适用性，因此，需要使用基于中国国情的修正阻抗函数[13]。

(3)

式中：tedge(ij)为车辆驶过路段eij的时间；v0(ij)为路段eij的自由流速度；α1和α2均为回归参数(α1取1.88；在高速、一级公路中，α2取4.9；在二、三、四级公路中，α2取7。

因不同等级公路对应着不同的通行能力和自由流速度，且同一等级公路中不同车道的通行能力和自由流速度也不相同。为简化模型和方便计算，各等级公路的通行能力取各车道的加和值，自由流速度取各车道的平均值，得到各等级公路(高速公路按6车道算，一级公路按4车道计算)的通行能力和自由流速度，见表1。

运输车队经过路段出口和交叉口等瓶颈处时常会出现“正常速度-减速-瓶颈速度-加速-正常速度”的过程。参考车流波动理论，可计算出车队经过每个路段出口的时间。假设车辆在路段中的正常速度为v，通过瓶颈段的速度为v′，驾驶员从看到前车减速到实施减速的反应时间为t，车队车辆数为n，两车之间的车头间距为lgap，瓶颈段长度为lb，则整个车队通过瓶颈段所需时间为：

表1 各等级公路数据Table 1 The road data for all grades

(4)

经过路径Pk的总时间为各路段时间与瓶颈处时间之和。

(5)

3.2 运输消耗

降低运输费用、实现低耗及高效运输是军事运输的重要目标。经济性指标由运输消耗来体现，而运输消耗中最明显且最易定量测量的项目就是油耗，因此，本研究以油耗作为运输的经济性指标。

在恒定速度的油耗研究中，较为常用的是POST经典模型。该模型能够直观、准确地反映运输车队匀速经过通行路径的油耗情况，适用于车队匀速行驶状态下的油耗求解。然而，POST模型不能准确计算车队在饱和度不为0的路段中行驶时的油耗情况。因为当车队在饱和度不为0的路段中行驶时，受到其他车辆的干扰，其速度往往不是恒定的。但并非完全无规律可循。朱建全[14]将机动车在饱和度不为0的路段中行驶时的加、减速情况用加速度绝对值的平均值来表示，并且指出：加速度绝对值的平均值随着路段饱和度的增加而减小。借鉴加速度绝对值的平均值与油耗的线性模型，结合POST经典模型，提出运输车队的油耗模型为：

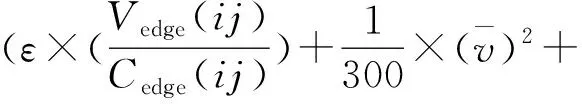
(6)

根据车队经过路段的时间与路段饱和度的关系式，可推导出车队经过路段的平均速度与路段饱和度的关系式为：

(7)

经过路径Pk所需要的总油耗为：

(8)

3.3 路径影响程度

目前，运输车队行进路径对区域公路网中社会车辆影响程度的度量较难求解，也没有具体的度量指标可直接应用。为此，本研究引入其他可度量指标来评价。运输车队出行对公路网的影响最终归结为社会车辆的行程时间变化。造成该变化的因素包括2个：① 交通管制引起交通量重分配，从而导致各路段行程时间发生变化(若无交通管制，则不考虑该因素)；② 运输车队在行进路径上的非管制路段中优先通行使得社会车辆的行程时间增加(假设车队通过出口位置的时间即为社会车辆在该路段行程时间的增加)。

公路网中各路段上的行程时间变化将会引起各OD对最短耗时路径的变化。为度量公路网的整体通行效率变化情况，引入网络效率变化率作为运输车队行进路径影响程度的指标。

3.3.1 网络效率

网络效率[15]能够较好地度量载体在网络上流动的有效程度。本研究将各节点之间的连接属性指标替换成最短行程时间，改进后能更好地衡量整个网络的运行效率。

(9)

式中：E为改进后的网络效率；tmn为节点vm和vn的最短行程时间；N为网络中节点的总数。

3.3.2 网络效率变化率

运输车队出行将导致公路网的网络效率发生变化，以网络效率变化率表示车队行进路径的影响程度。

(10)

式中：η为网络效率变化率；E和E′分别为车队出行前和车队出行后的网络效率；tmn和tmn′分别为车队出行前和车队出行后节点vm和vn之间的最短行程时间。

在进行最优路径的决策时，需综合考虑运输时间、运输消耗及影响程度3个指标。为求解多目标下的最优路径，引入灰色加权关联分析算法。

3.4 灰色加权关联分析算法

灰色关联分析法通过确定参考数列和若干个比较数列的几何形状相似程度来判断其联系是否紧密。其基本思想是将原始观测数进行无量纲化处理，计算关联系数和关联度，通过比较关联度的大小来判断比较数列的优劣，该方法在多个领域的应用获得了较好的效果。为求解最优路径选择，需在灰色关联分析法中引入指标权重[2]。具体步骤为：

1) 确定有效路径的分析数列

假设已通过限长路算法，求得OD对之间共有n条有效路径；路径优化指标有3个，则第k条有效路径的比较数列为：

Xk={Xk(1)，Xk(2)，Xk(3)}；1≤k≤n。

(11)

式中：Xk(1)，Xk(2)和Xk(3)分别为第k条有效路径的运输时间、运输消耗和影响程度。

有效路径的指标参考数列为：

Y={Y(1)，Y(2)，Y(3)}。

(12)

3个指标的最优值均为最小值，因此，Y(1)，Y(2)和Y(3)分别为比较数列中运输时间、运输消耗和影响程度的最小值。

2) 指标的无量纲化处理

观察到3个指标的量纲不一致，数值数量级不统一，需要对3个指标进行无量纲化处理。

(13)

处理后，得到比较数列为：

1≤k≤n。

(14)

参考数列为：

(15)

3)计算关联系数

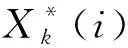
(16)

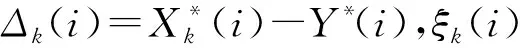
4) 确定指标权重

设运输时间指标权重为w1=θ1；运输消耗指标权重为w2=θ2；影响程度指标权重为w3=1-θ1-θ2。

5) 计算关联度

第k条有效路径的关联度为：

Coor(k)=ζk(1)×θ1+ζk(2)×θ2+ζk(3)×

(1-θ1-θ2)。

(17)

6)比较关联度的大小

依次计算出所有有效路径的关联度，比较其大小并进行排序，关联度最大的有效路径即为所求最优路径。

4 实例应用

选取某区域公路网为研究对象，将其抽象处理后形成拓扑图，如图2所示。图2中共含有63个节点，117条边。假设“标准路段”的初始饱和度为2，各路段的瓶颈处长度为100 m。

某运输部队接到任务后准备从节点v1处出发，前往节点v63处。根据此次运输任务的紧急程度，设定路径容忍系数为1.05，该运输车队包含50辆车。假设行车间距为50 m，车队通过路段出口处的速度为30 km/h，车辆的油耗饱和度系数为5，驾驶员减速反应时间为0.5 s。

图2 某区域公路网拓扑图Fig.2 Road topography of an area

由Dijkstra最短路算法，求得v1和v63之间的最短路径为Pshortest={v1，v3，v8，v15，v25，v39，v43，v52，v59，v63}，其长度为1 553 km，则路径容忍长度为1 630.65 km。采用限长路算法，求得v1～v63之间共有13条有效路径。将有效路径按长度排序编号后，依次计算其运输时间、运输消耗及影响程度。依据运输具体情况，设定交通管制的饱和度阈值为0.6，运输时间指标的权重取0.7，运输消耗指标权重取0.1，影响程度指标权重为0.2。使用灰色加权关联分析算法，依次求解各条有效路径的关联度，随后对有效路径关联度的大小进行排序，见表2。

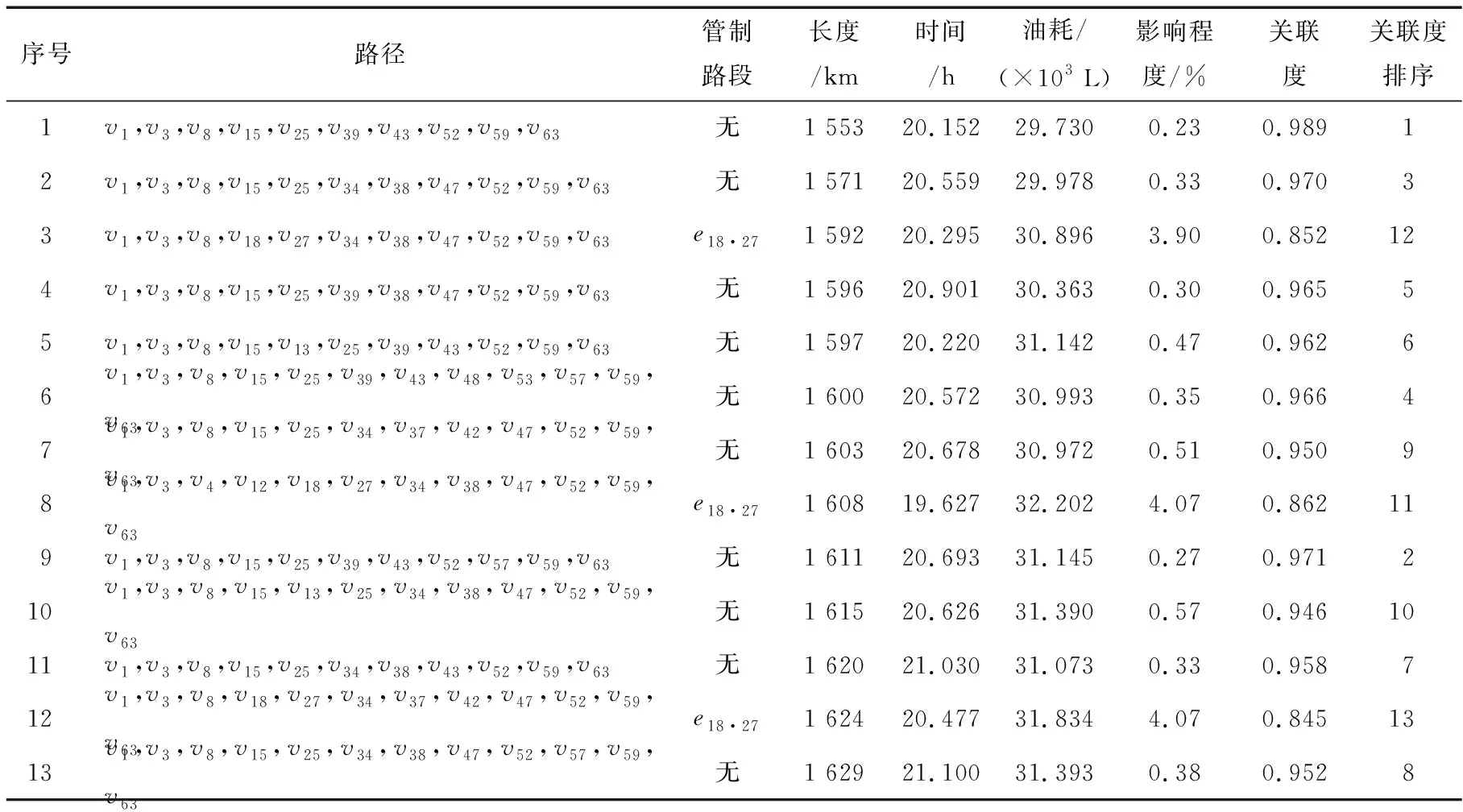
表2 路径关联度排序Table 2 Ranking table of path correlation

从表2中可以看出，关联度最大的路径为：P1={v1，v3，v8，v15，v25，v39，v43，v52，v59，v63}，其关联度为Corr(1)=0.989，为所求最优路径。除P1外，其余12条有效路径均满足运输任务的距离限制要求，可按照关联度的大小进行排序，并依据运输任务的具体情况作为备选路径。从表2中还可以看出，路径P3，P8及P12中包含管制路段，其影响程度较大，关联度较小。表明：平时条件下的交通管制对区域公路网的影响较大，但对运输路径的优化效果并不明显。因此，决策者在决定实施交通管制前应结合运输任务和实际需求慎重考虑。

5 结论

平时条件下军事交通运输的选路既关系到运输任务能否及时、有效地完成，也关系到运输耗费和对民用运输的影响，应在保证运输任务完成的基础上统筹兼顾时效性、经济性及低影响性，科学、合理地选取最优运输路径。实际运输过程中，决策者可根据运输任务的具体情况调整路径的容忍系数和最优路径，求解过程中的各指标权重，使最优路径求解结果更符合于实际任务的需求。当最优路径临时失效时，可依据关联度的大小选用备份路径。

本研究使用边介数对路段初始交通量进行赋值，与公路网的实际交通量存在着一定的差异。利用现代化的监测手段，获取实时交通状况，并采用模拟仿真的方法，构建交通量的变化模型将成为下一步改进的方向。