落角约束最优制导律在空地导弹上的应用*
陈 韵,常 燕,苗昊春,严宪军
(1 西北工业大学航天学院,西安 710072;2 火箭军工程大学,西安 710025;3 西安现代控制技术研究所,西安 710065)
0 引言
随着武器作战样式的变革,在精确打击运动装甲目标的武器系统设计中,除了命中精度这项基本要求外,还需要在命中时刻具有一定的命中角度,以提高战斗部的毁伤效能。近年来具有终端角度约束的制导方法受到越来越广泛的关注,国内外学者进行了很多相关研究,根据理论基础的不同,具有终端角度约束的制导律主要有过重力补偿比例导引律,变结构制导律,最优制导律以及其他类型的制导律[1-7]。过重力补偿比例制导律[2]原理简单,易于工程实现,但只能用于增大落角,不适用于小落角的情况,且对于落角期望值>30°的情况也不能很好适应。采用变结构理论[3]的带落角约束制导律也有较多的研究,对机动目标具有较好的鲁棒性,但是变结构控制容易存在振颤问题。
目前直升机载空地导弹通常配装有多种战斗部。配装破甲战斗部时,采用大角度顶攻方式可以对地面装甲目标进行有效毁伤;但对于坚固的工事目标,攻坚战斗部又对制导系统提出了小角度平射攻击方式的要求。文中利用最优控制理论研究带有落角约束的制导律,通过设置不同的期望落角值,实现一套制导控制系统适应多种落角的需求。
1 相对运动建模与分析
导弹接近目标过程中与目标的相对几何关系见图1。图中:Oxy为导弹运动纵向平面;M为导弹,在发射坐标系中的坐标为(xm,ym);V为导弹速度,速度方向与水平面夹角θ即弹道倾角,速度方向与弹目线夹角η;T为目标,在发射坐标系中的坐标为(xt,yt);q为弹目视线角。
根据导弹目标角度和几何相对关系,可以得到相对运动方程[8]:
(1)
为保证导弹能精确命中目标,必须设计合适的制导律来控制导弹的飞行路径。制导律是指作用于导弹的法向加速度ac与弹目相对运动状态的关系,其中:
(2)
2 最优制导律
基于最优控制原理推导带落角约束的制导律。
对式(1)中的第二项进行微分可以得到:
(3)
建立状态方程
(4)
其中:
θf为弹道终端落角期望值。
对于各状态变量,起始时刻有:
终端条件为:
x1(tf)=0x2(tf)=0
考虑到终端约束,选择如下二次型性能指标:
(5)
式中:
为加权矩阵,此处F→∞。由最优控制理论可知,最优控制解为:
(6)
式中:R=1,
P为满足以下Riccati方程的解:
(7)
令:
则式(7)可以表示为:
(8)
因q12=q21,则有:
(9)
由式(9)中第三式可得:
(10)
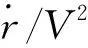
(11)
将式(11)代入式(9)的第二式,则有:
(12)
将自变量t变为r,可得:
(13)
当t=tf时,q22(tf)=0,r(tf)=0,近似认为V为常值,则有:
(14)
(15)
从而可求解得到逆矩阵P-1:
(16)
则:
(17)
代入式(6)得到最优控制:
(18)
即:
(19)
根据式(2)可以得到具有角速度反馈形式的最优制导律表示为:
(20)
从式(20)中可以看出,最优制导律中的第一部分与传统的比例导引制导律一致,与视线角速度成比例关系,确保导弹命中目标;增加的第二项即是角度约束项,以保证命中点处的速度方向满足要求。
3 仿真验证
3.1 仿真条件
落角约束最优制导律仿真验证原理框图见图2所示。
以某直升机载空地导弹为例进行落角约束制导律的仿真验证。设导弹初始发射高度为300 m,导弹飞行速度约为200 m/s,目标距离为5 000 m,采用发射前锁定攻击模式。建立六自由度弹体运动模型,对最优制导律进行仿真验证。
从章节2的推导分析可知,只要设置期望落角值θf,利用式(20)的最优制导律可以实现导弹以弹道倾角θ(tf)=θf,精确命中目标。
3.2 仿真结果
分别设置期望落角值θf值为0°、-15°、-30°、-45°。落角、脱靶量仿真结果见表1,仿真曲线见图3~图5。

期望落值/(°)实际值/(°)脱靶量/m0.00.2930.056-15.0-14.960.022-30.0-29.950.034-45.0-44.480.083
从图3可以看出,期望的落角绝对值越大,弹道需要爬升的高度越高;从图4可以看出导弹命中时刻的倾角与期望值基本一致;从图5可以看出飞行过程的需用过载在-2g~+4g范围内,满足导弹可用过载能力;从图6可以看出,导引头框架角在-25°~+10°范围内,满足导引头技术指标。
4 结论
目前直升机载空地导弹对末端落角提出了多种要求,文中研究的是一种最优制导律,在满足精度的前提下,可实现导弹能力范围内对目标的任意落角攻击。经仿真分析表明:
1)该制导律基于最优控制理论推导得到,由两部分组成,第一部分与比例导引一致,满足命中精度,第二部分与弹目相对关系及期望落角相关,实现落角约束。
2)该制导律通过对弹道的抬高来实现对落角的增大,且需用过载及导引头框架角均满足要求。
3)该制导律实现的需用信息均可在弹上通过制导部件获取,公式简单,易于工程实现。

