多耦合作用下的飞行器动力学综合解耦方法研究*

董诗萌,闫智强,卢娟芝,马 骏,成 高,姜 智

(西安现代控制技术研究所,西安 710065)

0 引言

高超声速飞行器在追求更高飞行速度的同时也带来了不同于常规的诸多问题,主要包括以下几个方面:高马赫数、大空域飞行条件下飞行环境恶劣变化,面对称气动布局下气动/运动/惯量耦合严重,以及飞行器机体与发动机一体化带来的相互作用等[1]。在此情况下,多种耦合特性同时作用于飞行器整体系统,工程实际中针对单输入-单输出系统的性能评价指标不再适用,使得高超声速飞行器控制系统设计变得复杂。

目前国内外多变量系统的解耦方法有特征模型解耦、耦合补偿及等效舵解耦等[2]。等效舵解耦方法针对飞行器偏航/俯仰通道设计单输入单输出自抗扰控制器,实现飞行器的姿态控制[3]。等效舵解耦方法针对飞行器偏航/俯仰通道的气动交叉耦合,把气动耦合表征为附加舵偏的形式,设计了解耦控制器[4]。然而这种解耦方法仅考虑气动耦合项,并没有推广到惯性、运动耦合等其他耦合因素的研究中。

文中开展了多种耦合作用下的飞行器动力学模型分析和综合解耦方法的研究,给出了飞行器综合耦合评价体系和耦合等效处理方法,实现了飞行器动力学模型各通道的解耦,使之能够应用工程上常用的经典控制理论设计和评价方法。

1 耦合特性分析与各耦合模型建立

文中以X-43A高超声速飞行器为研究对象。

1.1 面对称外形引起的气动耦合

(1)

1.2 BTT飞行方式所带来的运动耦合

高超声速飞行器机动性能要求高,而X-43A采用面对称气动布局只有一个有效升力面,采用BTT-180运动方式。当飞行器以较高的滚转速率运动时,滚转速率将引起俯仰和偏航运动之间的交叉运动耦合。

(2)

1.3 非轴对称体所带来的惯量耦合

由于面对称乘波体的气动外形关于纵向平面x1oy1对称,转动惯量积Iyz=Izx=0,惯量耦合主要由惯量积Ixy和惯量差(Iz-Iy)、(Ix-Iz)、(Iy-Ix)引起,体现在飞行器的姿态动力学方程中。

(3)

式中MTh为推力力矩。

1.4 吸气式发动机工作所带来的推力耦合

吸气式超燃冲压发动机的进气压缩面和尾喷管分别为飞行器的前体和后体,而飞行器在不同的推力作用下,其飞行速度、气动角、受到的气动力、姿态等随之改变,从而形成飞行器机体姿态和推力作用之间的耦合效应[7]。将超燃冲压发动机推力模型在工作点小扰动线性展开,利用敏感度方程、敏感度矩阵的形式建立飞行状态对发动机的耦合模型[8-9]:

Th=Th0+k·η

(4)

1.5 尖薄前缘外形所带来的结构弹性耦合

由于高超巡航的需要,X-43A为减少阻力将外形前缘设计的很尖,同时控制面也相应很薄。文中借助于ANSYS有限元分析软件,求得气动力作用下机体前缘的变化,进而求得气动角的变化值,将结构弹性耦合归结为气动角的变化。在小位移的情况下,机身前部的攻角变化量Δα′为:

Δα′=arctan[y(xf,t)/Lf]

(5)

式中：Lf为机身前部的长度;y(xf,t)是机体前缘的形变量。

针对特征点分析发现,气动力和力矩受结构弹性耦合影响很小,而冲压发动机对其变化敏感。因此可以不考虑机体的结构弹性问题,而将结构变形引起的攻角变化合并进推力耦合研究中,则推力耦合的气动角定义变为:

η=Δα+Δα′

(6)

式中：Δα为飞行器姿态变化引起的攻角变化;Δα′为结构弹性耦合引起的局部攻角变化。

2 单独耦合因素评价指标定义与特性划分

2.1 耦合度定义

在多变量控制理论中,通常利用行半径系数对评价系统的耦合程度。对常数矩阵B={bij}∈Cm×m,有：

(7)

称为矩阵B第i行的行半径系数。当满足ρi<1时,认为该矩阵具有对角优势阵。

文中采用力矩的形式来描述耦合特性对飞行器运动的影响,多种耦合因素用统一的物理量纲归一化,方便用行半径系数的分析方法分析耦合因素。为了分析不同耦合因素对本通道的影响作用大小,首先引入单独耦合因素耦合度的定义:

%

(i=x,y,z)

(8)

式中：通道i分别取滚转通道x、偏航通道y、俯仰通道z;m可分别取气动角引起的稳定力矩耦合项α/β和β/α、操纵力矩耦合项δ、阻尼力矩耦合项ω、惯量耦合项I以及机体姿态变化和弹性形变引起的推力耦合项Th。

耦合度反映了一种耦合因素对主通道力矩的耦合影响程度,耦合度越大,则主通道的力矩越容易受到其他通道这种耦合因素的影响。当耦合度大于1时,主通道不占有优势,耦合影响严重。

气动耦合、惯量耦合的耦合度度量和解耦方法在俯仰、偏航、滚转通道完全相同。而推力耦合和结构弹性耦合则主要作用于飞行器的纵向运动状态中,其耦合度度量和解耦方法在俯仰通道开展。

2.2 耦合度上限

解耦方法对于解耦问题是有上限的,根据飞行器的控制能力而定。耦合增大到一定数值时,舵面的偏转不能满足需求,舵能力不足,系统变得不稳定,无法实现解耦,定义可控临界点对应的耦合度为可控耦合度。设耦合上限为klim,则：

(9)

可以解得:

(10)

3 综合耦合度定义与解耦方法

飞行器的各种耦合作用相互影响,互为成因,即便单独耦合度相同,由于不同类耦合的数值量级不一致,对系统的干扰权重大小也不一样。此外,各耦合特性对飞行器某一通道运动状态量的影响同极性时,该通道交联效应更加显著,耦合特性增强,形成干扰累积问题。耦合度作为单独耦合因素评价指标,无法解决干扰权重和干扰累积的问题,有必要引入各种耦合综合作用下的耦合特性评价指标和解耦方法。

3.1 综合耦合度定义

综合耦合度定义为其他因素引起的耦合力矩的绝对值和与本通道主力矩绝对值的比值。飞行器三通道的综合耦合度分别定义为:

(11)

其中,L1为飞行器质心到发动机推力线的距离。

3.2 综合耦合度上限

综合耦合度是表征一个通道的力矩受到其他通道耦合影响的程度,综合耦合度上限是指当飞行器某通道所受到耦合力矩与本通道的主力矩之比不大于上限值Kb时,主通道因素产生力矩占优,控制器的稳定裕度能够解决小耦合带来的干扰。综合耦合度上限取5%～20%之间,由于飞行器机体特性和飞行弹道包络特点的不同,综合耦合度上限定义随之不同。

3.3 综合解耦方法

根据综合耦合度的定义,综合耦合度用以判定各种耦合因素互相影响、累积的综合作用,超过综合耦合度上限Kb时,说明耦合力矩项综合作用影响较大,不可直接忽略,需要将飞行器其他通道力矩耦合项等效为本通道相应的力矩项。以俯仰通道为例,具体方法为:首先计算出综合耦合度,对于超过综合耦合度上限的,将稳定力矩耦合等效为:

(12)

将操纵力矩耦合等效为:

(13)

将阻尼力矩耦合等效为:

(14)

将惯量力矩耦合等效为:

(15)

将推力力矩耦合等效为:

(16)

其中,上式右侧的极性符号由耦合项与主通道极性异同而判定。

根据单独耦合度的定义,单独耦合度的上限为klim,确保飞行器各通道耦合干扰不超出飞行器控制能力,也是解耦的极限能力,耦合度大于极限值则解耦失败。当单独耦合度超过1时,主通道失去对角优势,即使综合耦合度小于上限,也同样不可直接忽略,需要进行等效变换处理。解耦方法流程如图1所示。

4 算例分析与方法验证

根据图1所示的飞行器综合解耦方法流程,以X-43A为研究对象,验证所提出解耦方法的合理性和有效性。针对巡飞段爬升最高点为例,建立对象飞行器动力学耦合模型如式(17)。

(17)

在特征点处存在惯量耦合、气动耦合及推力耦合。结合对象飞行器标称气动、惯量及推力数据,计算飞行器特征点处单独耦合因素耦合度及综合耦合度,如表1所示。

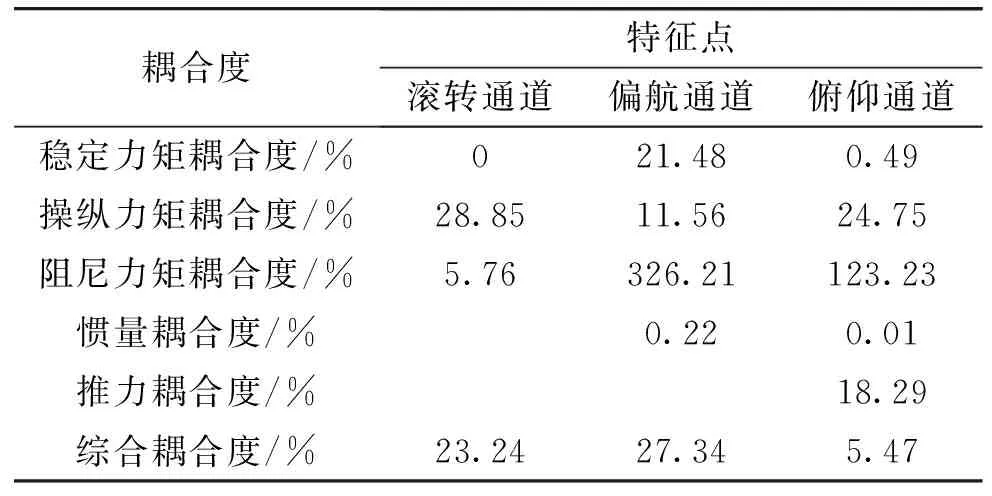
表1 算例飞行器的耦合度

经综合解耦,算例飞行器三通道解耦模型为:

(18)

由式(18)可以看出,三通道动力学模型在解耦后不含耦合项,解耦方法实现了对耦合系统的综合解耦。针对不考虑耦合的三通道独立模型和采用综合解耦方法的解耦模型分别进行控制器设计,将两组控制器参数代回飞行器耦合模型中,对比解耦前和解耦后的输出性能。仿真初始条件:高度H=26.2 km,Ma=5.8,攻角α0=0°,侧滑角β0=1°,倾侧角γ0=5°,仿真结果如图2所示。

由图2可以看出三通道独立设计的控制器代入飞行器耦合模型时很难保证指令的执行。而相比而看,针对解耦模型设计的控制器可以很好地控制耦合模型,攻角和倾侧角调节时间短,侧滑角控制效果好。为了进一步验证解耦方法的可靠性,分别对气动参数和转动惯量进行拉偏处理,仿真结果对比如图3所示,在标称和正负拉偏情况下均可以快速跟踪指令。

5 结束语

文中提出了一种飞行器整体系统的综合解耦方法,解决了多种耦合作用下的飞行器动力学解耦问题。

方法引入度量耦合影响程度的耦合度概念,对各种耦合因素进行划分与归类,将耦合项进行忽略或等效处理,从而实现了飞行器动力学建模解耦。仿真结果验证了综合解耦方法的有效性,以及在不确定性因素存在时的可靠性,该方法对于高超声速飞行器解耦建模具有一定的指导意义。