基于高斯伪谱法的制导火箭弹总体优化设计研究*

杨 靖,毛 瑞,杜凤怀,白风科,黄若超

(西安现代控制技术研究所,西安 710065)

0 引言

制导火箭武器系统因其反应迅速、火力猛、威力大、成本适中,火力密度高等特点,近年来受到很多国家重视[1]。制导火箭弹作为一个系统,其总体性能的优劣依赖于各子系统的性能以及各子系统之间的协调配合。为提高毁伤效果,杀伤爆破型或侵彻型等战斗部往往要求制导火箭弹以大落角命中目标并具有一定的末速。由于飞行过程中,只有发动机推力和阻力做功,全弹道速度方案主要依赖于发动机推力方案设计和弹道方案设计。兼顾战斗部要求和发动机推力方案,寻找合适的飞行弹道,优化发动机技术指标,对火箭弹总体设计具有重要的现实意义。

制导火箭弹飞行弹道的优化问题实质是最优控制问题。由于描述制导火箭弹运动的非线性常微分方程组较为复杂,大空域飞行过程中空气动力非线性特性突出,且控制变量和状态变量往往具有约束,一般难以解析求解弹道优化问题,只能寻求数值解。高斯伪谱法与传统直接法等数值方法相比,因其参数化得到的非线性规划问题的karush-kuhn-tucker(KKT)条件与离散的哈密顿边值问题的一阶最优性条件具有一致性[2],近年来受到国内外广泛关注。一个典型和显著的应用是用于完成被称为“零推进剂机动”的国际空间站大规模姿态调整任务,通过基于伪谱法的轨迹优化,为NASA节省了100万美元的推进剂经费[3-4]。国内学者也开展了大量的相关研究。杨博[5]等人基于高斯伪谱法研究了化电混合推进剂系统转移轨道优化设计问题。张佩俊等人针对复杂多约束条件下空天飞机上升段燃料最优控制问题,提出了一种基于高斯伪谱法的空天飞机上升段轨迹优化策略[6]。

文中针对制导火箭弹总体优化设计问题,提出了一种基于高斯伪谱法的总体优化设计方法。为优化发动机技术要求,确保战斗部对飞行弹道的大落角和末速要求,将落角作为终端约束,取目标函数为最大化末速,进行了方案弹道优化,为发动机技术要求的优化提供参考。

1 总体优化设计模型

1.1 制导火箭弹运动方程

假设地面坐标系为惯性系,制导火箭弹视为可控质点,仅考虑纵向平面内的运动,攻角响应近似为一阶惯性环节,则制导火箭弹的运动模型可简化表述为:

(1)

式中:V为质心速度;θ为弹道倾角;x与y分别为纵向平面内的质心位置;m为质量;P为发动机推力;q为动压;S为特征面积;阻力系数cx和升力系数cy是马赫数和攻角α的函数;重力加速度g随高度变化;mc为质量流量;Tα为攻角响应时间常数;αc为攻角指令。

1.2 优化问题描述

1)性能指标

为保证战斗部的毁伤效果,将性能指标取为末端速度最大,即:

J=maxVf

(2)

2)初始状态约束

初始状态为制导火箭弹发射点状态:

(3)

3)终端状态约束

针对固定目标,对弹着点状态进行约束:

(4)

4)控制变量约束

由资历高、经验丰富的高级职称人员组成专家组，参照有关管理规定、处方管理条例、单位及科室具体情况等，制定系统的用药规范和细则，印刷后发放给各个科室。同时专家组制定药物处方评估标准，内容应包括药物的使用频率、药物利用指数、药物的耐药性情况、处方的合理性等方面[3] 。

考虑制导火箭弹的稳定性能与控制性能,对攻角指令进行限制:

(5)

2 高斯伪谱法

高斯伪谱法是一种将连续最优控制问题转化为非线性规划问题的参数化方法。高斯伪谱法的基本原理为:将状态变量和控制变量在一系列高斯点上离散,并以所选高斯点为节点构造全局拉格朗日插值多项式来逼近状态变量和控制变量,以全局插值多项式的导数近似系统的动力学方程,从而将微分方程组约束转化为代数方程组约束。性能指标中的积分项由高斯积分计算。终端状态由初始状态和对右函数的积分获得。经上述变换,可将连续最优控制问题参数化为非线性规划问题。

2.1 系统微分方程的离散

考虑一般形式的非线性系统动力学方程:

(6)

式中:x∈n为状态向量;u∈m为控制向量;f:n×n×→n为连续向量函数。为应用正交多项式的性质,采用高斯伪谱法需要将时间区域[t0,tf]转换到[-1,1]上,为此引入变量τ对时间t进行变换,即:

(7)

从而,系统动力学方程转化为:

(8)

选取N个Lagrange插值基函数Lk近似逼近状态向量,可得:

(9)

(10)

其中,τk(k=0,…,N)为如下N次Legendre正交多项式的零点:

(11)

对式(9)求导,可得以插值多项式导数为近似的状态变量的导数:

(12)

其中,微分矩阵D∈N×(N+1)通过下式计算:

(13)

将式(12)代入式(8),得到状态向量在配点上应满足的代数约束:

(14)

综上所述,将系统动力学微分方程参数化为了代数方程约束。

2.2 终端约束的离散

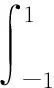
积分动力学方程(8)可得终端状态:

(15)

采用高斯积分公式近似上式中的积分项,可得离散化终端状态:

(16)

通过上述离散过程,将方案弹道优化问题转化为了非线性规划问题,其设计变量包括离散点的状态向量(X1,X2,…,XN)和控制向量(U1,U2,…,UN)及终端时刻tf,其约束条件为动力学方程约束及边界条件约束。目前对于非线性规划问题的数值求解方法有很多,贯序二次规划算法因其稳定性和精度优势应用最为广泛。因此,文中采用贯序二次规划法对经高斯伪谱法离散化的方案弹道优化问题进行求解。

3 数值仿真分析

以某制导火箭弹的总体论证为例,进行数值仿真分析。为保证某型战斗部的毁伤效果,需要约束落角和末速。在方案弹道优化中,将落角作为终端约束条件,目标函数为最大化末速,射程依次取为25 km、35 km、45 km、55 km、65 km、75 km、85 km、110 km、130 km,来验证发动机方案能否在全射程范围内满足战斗部的技术要求。

制导火箭弹初始状态约束为:x0=0,y0=0,α0=0,20°≤θ0≤55°,V0=25 m/s,m0=342 kg。终端弹道倾角约束取为θf∈[-90°,-80°]。气象条件采用空军标准气象条件。

图1给出了不同射程制导火箭弹速度随时间的变化曲线。图2展示了不同射程弹道倾角随时间的变化曲线。表1列出了不同射程对应的落角和末速。可以看出,在保证落角约束的条件下,随着射程的增加,末速最大值先减小后增大再减小。这是由于火箭弹飞行过程中只有发动机推力和阻力做功。仿真中,不同射程发动机参数一致,发动机工作过程阶段,火箭弹飞行轨迹差异不大,所以发动机推力做功对于不同射程差别不大。阻力系数与飞行高度和马赫数相关,25 km到130 km的射程对应的弹道高变化范围较大,高空飞行占总飞行过程的比重较大时,阻力做功相对较小,末速较大;另外,总飞行路径较短,阻力做功相对较小,末速较大。

图1 不同射程速度随时间的变化曲线

图2 不同射程弹道倾角随时间的变化曲线

射程/km落角/(°)末速/(m/s)2580.65448.43580.83434.74581.12434.35580.44449.56580.31465.77580.28480.68580.17493.211080.10591.913080.06520.1

4 结束语

文中针对制导火箭弹总体优化设计问题,提出了一种基于高斯伪谱法的总体优化设计方法。为优化发动机技术要求,确保战斗部对飞行弹道的大落角和末速要求,将落角作为终端约束,取目标函数为最大化末速,进行了方案弹道优化。通过数值仿真,给出了在满足落角约束条件下最大末速随射程的变化规律。仿真实例中,射程跨度较大时,制导火箭弹弹道式飞行高度变化范围较广,在保证落角约束的条件下,随着射程的增加,末速最大值先减小后增大再减小。因此,在工程实践中,对于大射程跨度大空域飞行制导火箭弹的总体方案技术指标分解,不能仅选取最近射程和最远射程进行验证,要充分验证全射程范围的可行性。