搭建有效平台 优化探究过程

刘艳红

时下，数学课堂倡导“以生为本”。细观我们的课堂，总会发现许多教师“穿新鞋，走老路”，并未彰显学生个性，凸显学生的主体地位。究其原因发现，课堂上许多教师教学方式单一，问题设计细碎、模糊、针对性不强，自我展示机会少，课堂互动不深入，导致学生思维受限制，在课堂中无法深入理解教学内容。如何改变以上现状呢？笔者认为，有效地给学生搭建探究的平台，让学生积极主动探究才能优化我们的课堂过程。

笔者以自己执教的“求多边形内角和”为例，谈谈自己的做法。

【环节一】提出问题，引发思考

（课件出示直角梯形图）

提出问题：你能想办法求出直角梯形的内角和吗？先自己独立思考，

想好的同学在自己的作业纸上写一写画一画。

学生进入自主探究环节，教师巡视。

几分钟之后，教师收集学生不同做法。

【环节二】交流展示，明确方法。

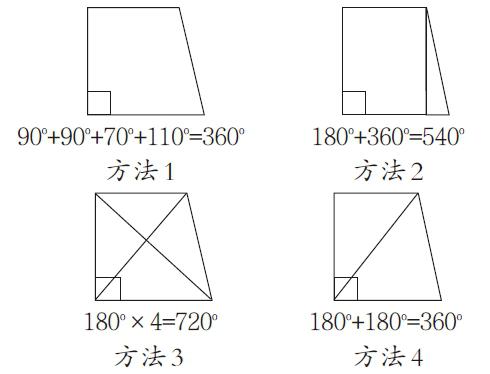
（展台出示4种做法）

90o+90o+70o+110o=360o           180o+360o=540o

方法1                       方法2

180o×4=720o               180o+180o=360o

方法3                      方法4

提出问题：仔细观察这几种方法，他们做得对吗？是怎样思考的？

生1：方法1是用测量的方法量出4个内角然后相加和是360°。

生2：用测量的方法是可以的，比较麻烦，还容易产生误差，测量时不够准确。

生3：方法2用分割的方法，把梯形分成一个长方形和一个三角形，用长方形内角和加上三角形内角和就是这个直角梯形的内角和。

生4：我反驳第二种方法，直角梯形的内角和指的是哪些角的和？

方法2的同学幡然醒悟。

生5（方法3的同学）：那我做的结果也是错误的了，分成的图形也增加了内角。

部分孩子开始反思这种做法……

生6：这两种方法都是可行的。两种方法只要减去增加的内角就可以了。方法2只要把长方形和三角形的内角和加过之后再减去多出来的两个直角就可以了，也就是540°-180°=360°。方法 3应该用720°减去增加的四个角形成的周角 360°才是直角梯形的内角和。

师：（投去赞许的目光）孩子们真爱思考，不用老师讲自己就能分析解决问题。

师：第三种做法对吗？分割成的两个三角形有没有增加新的内角？（没有增加）

小结：刚才我们用测量法和分割法两种方法探究了直角梯形的内角和，哪一种方法更有利于我们探究多边形内角和？（分割）分割的方法更有利于我们探究多边形内角和。分割时不要增加新的内角最为稳妥。

【环节三】深入探究，优化方法

提出问题：你能用这种分割的方法研究五边形内角和六边形内角和吗？

学生独立思考进行分割，教师巡视。

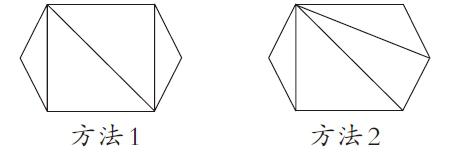
对照五边形分割及内角和之后出示两个同学不同分割六边形画法。

提问：这两种分法你更喜欢哪一种？  说出你喜欢的理由。

生1：分法一样的呀！都是把六边形分成了四个三角形？（感到疑惑）

生2：第一种是随意分割的，而第二种方法思考有序，是从一个顶点出发依次连接相对的顶点。我喜欢第二种。

小结：分割多边形时从一个顶点出发，有序分割，就能不重复不遗漏。

反思：

（一）问题引领，促进有效探究。

古人云“学起于思，思源于疑”。学生的思维一般从问题开始的，有了问题才有探究欲望。基于此，教师课前就必须针对本课内容精心设计好问题，给学生搭建探究平台，让学生处于主体地位，从而促进探究的有效性。

教学之前，笔者深入研究教材，发现教材提供的教学素材过多，孩子没有一个明晰的主线，不能有效引领学生进行深入的交流与对话。笔者对教材进行了重新设计，为学生提供明晰的值得思考的话题。

“你能想办法求出直角梯形的内角和吗？先自己独立思考，想好的同学在自己的作业纸上写一写画一画。”“仔细观察这几种方法，他们做得对吗？是怎样思考的？”“你會用分割这种方法研究五边形内角和六边形内角和吗？”

三大问题引领孩子深入探究，经历思考、探究、讨论、展示、提升的过程，获得真正的学习体验。

（二）提供平台，展现思维方法。

当学生独立思考探究出“直角梯形的内角和”时，我收集了学生4种不同方法，提供交流平台，抛出“仔细观察这几种方法，他们做得对吗？是怎样想的？”的话题，让学生有分析、辨析的话题，孩子们非常积极踊跃，他们有表现自我的机会。在交流中孩子们不但要反思自己解决问题的过程，而且质疑他人的观点，做出辩驳，补充。在畅所欲言，辨析明确中，表达自己的思考过程，体会到解决问题的多渠道，同时培养了孩子分析问题和解决问题能力。问题解决的价值不就是体现在能力的发展上吗？

（三）优化方法，加快探究进程。

在教学中我们要尊重孩子的个性思维，同时要在对辨析进行引导，让学生比较、分析，汲取他家之长，改进自己的方法策略，从中筛选，优化。在教学环节一、二中都出现不同问题解决策略。 “哪一种方法更有利于我们探究多边形内角和？”“这两种分法你更喜欢哪一种？”通过学生的辨析后，思维不断明晰。 “分割的方法更有利于我们探究多边形内角和。还有分割的方法中第三种方法最好，它没有增加新的内角。”“我喜欢第二种，这样方法思考有序。” 在反思中进行自我优化，为接下来探究多边形内角和的规律提供方法支持，学生的思维得到进一步升华。

【作者单位：徐州市铜山区三堡实验小学  江苏】