油船冰区舷侧结构的优化设计

杨 宜

（意大利船级社大中华区船舶部，上海200052）

0 前言

极地具有重要的战略价值。近年来，随着全球变暖，海冰融化，蕴藏丰富资源的北极新航道有望进一步开辟。适用于极地航行的船舶是在极地进行有关活动的必要条件［1］。本文以一艘10万吨级航行于冰区的成品油船舷侧结构为例，根据意大利船级社钢质海船规范，参考了芬兰海事局的冰级规范和指导性文件，进行了结构优化分析，分析表明在满足规范要求的前提下，不同的纵骨间距可能产生减重和减少焊接工作的效果，从而为结构设计提供一种新的思路。

1 芬兰—瑞典冰级规范

根据芬兰-瑞典冰级规范 （Finnish-Swedish Ice Class Rule，FSICR），在冰区加强区域内，所有骨材应与支持结构作有效的连接。纵骨应与所有支持的强肋骨和舱壁用肘板相连。当骨材通过支持结构时，骨材的腹板两面应与支持结构直接焊接相连，或采用领板或补板连接。设置肘板时，其厚度应至少与骨材的腹板相同，且边缘应作适当加强以抵抗屈曲［2-4］。

冰区载荷测量研究表明，在波罗的海航行的船舶所承受的冰压，有时会超过规范规定的值，从而导致应力超过屈服极限。但是通常认为如果采用骨材的材料和尺寸满足载荷实际测量最高值的要求，是很不经济的做法，所以一些超过许用应力的设计也都被接受了。在极端的情况下，结构会发生永久的塑性变形，而应用非线性有限元方法可以分析出这种塑性变形的大小［5］。

2 冰区舷侧结构规范设计

根据FSICR，设计冰压p应不小于式（1）计算所得值：

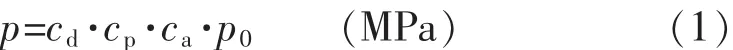
式中：cd——船舶尺度和主机输出功率影响系数；

cp——对于所考虑冰级的设计冰压在某一船体区域出现概率的系数；

ca——计算区域全长范围内冰压同时发生概率的系数；

p0——名义冰压，取值为5.6 MPa

对于纵骨架势外板，其厚度不小于式（2）计算所得值：

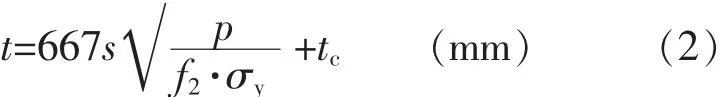
式中：s——纵骨间距，m；

f2——系数，具体参见FSICR；

σy——材料的屈服应力，MPa；

tc——腐蚀增量，一般取2 mm

对于舷侧纵骨架势纵骨，其剖面模数W和有效剪切面积A应不小于式（3）～（4）计算所得值：

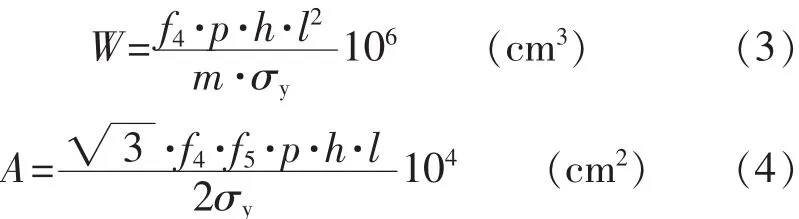
式中的参数参见FSICR。

本文中分析的10万吨级成品油船的冰级符号为IB，其主尺度见表1。

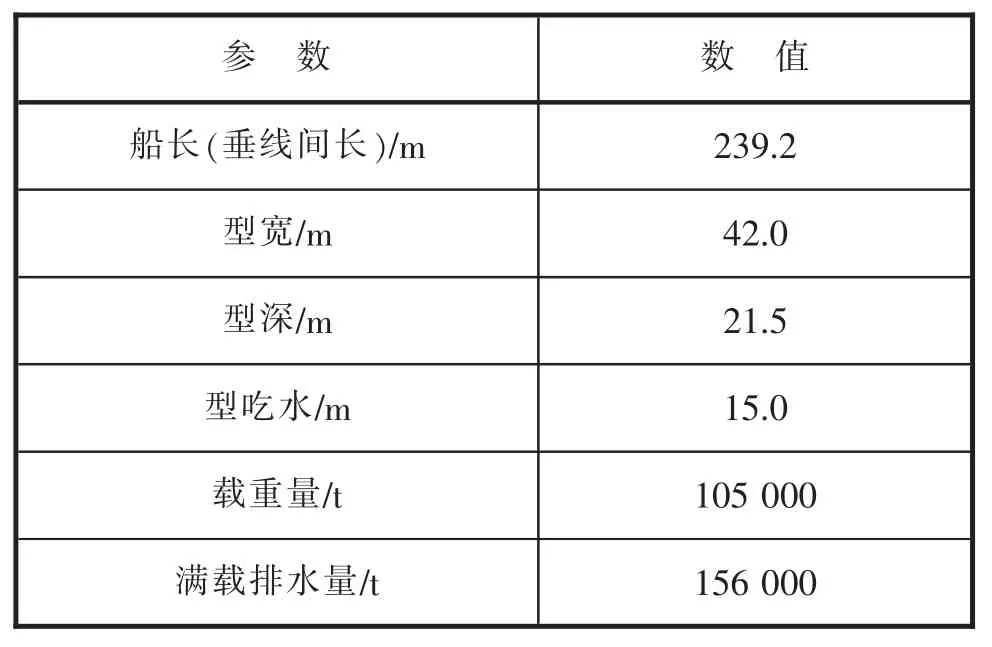
表1 10万吨级成品油船主尺度

所要研究的纵骨架式舷侧平台之间的距离为3.6 m，强框间距为3.78 m。所研究的纵骨间距分别为 300 mm、360 mm、400 mm、450 mm、600 mm 和720 mm，结构的材料均为AH32高强度钢，如图1所示。

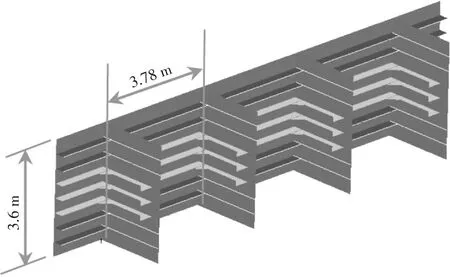
图1 纵骨架势舷侧

根据FSICR规范计算的结果见表2和表3。纵骨的选择根据国际标准 ISO 657-18∶1980（E）。

从规范计算的结果可以看出，纵骨间距对于外板厚度的影响比较大，而对于纵骨的选择起决定作用的是有效剪切面积的要求。

在不同的纵骨间距下，舷侧平台之间的一个单位跨距的外板板架的结构重量计算见表4～5。钢材的密度取 7.85×103kg/m3。

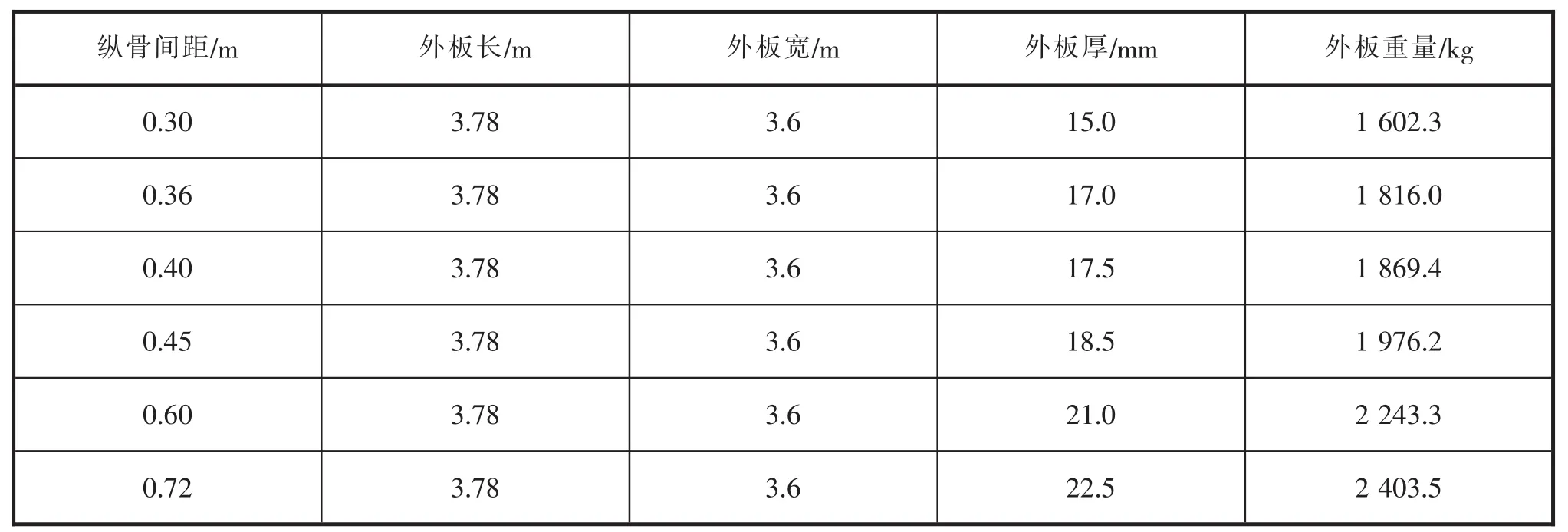
表4 单位跨距内外板的重量计算

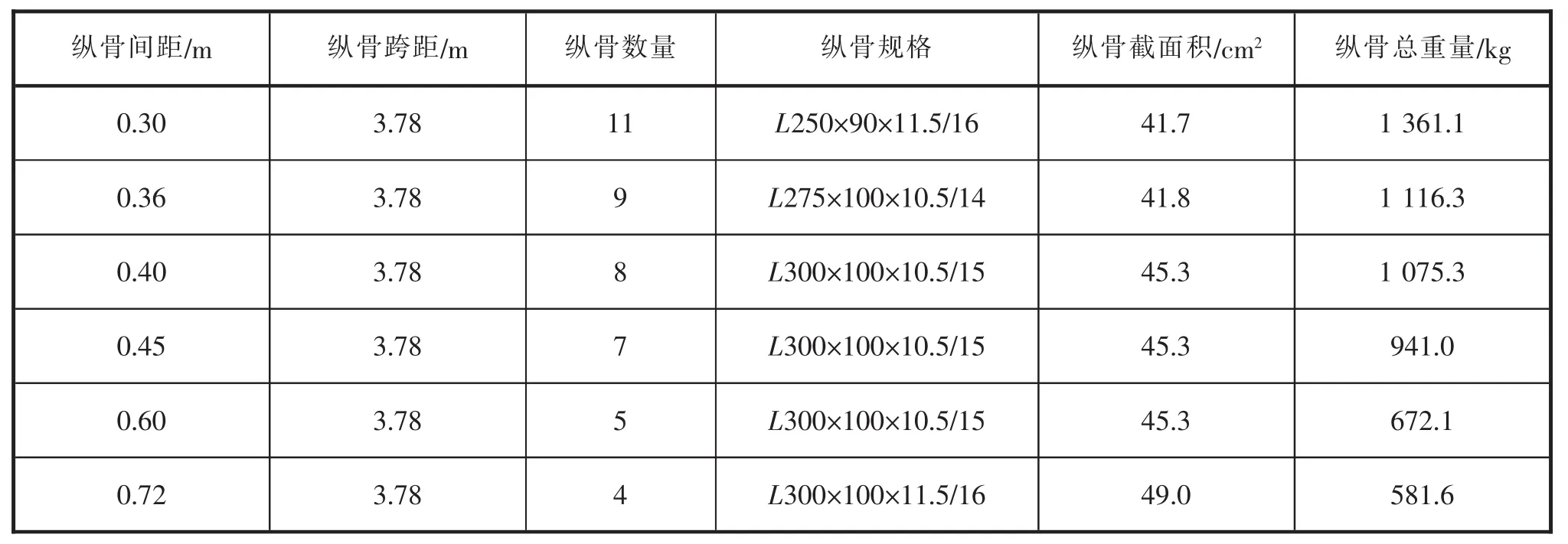
表5 单位跨距内纵骨的重量计算

由表4～5可见，不同纵骨间距下的冰区加强外板板架的质量情况如图2所示。从外板板架质量分布的情况可以看出，并不是纵骨间距越大越好或者是越小越好，而是存在一个中间值，使得外板和纵骨的组合恰到好处。

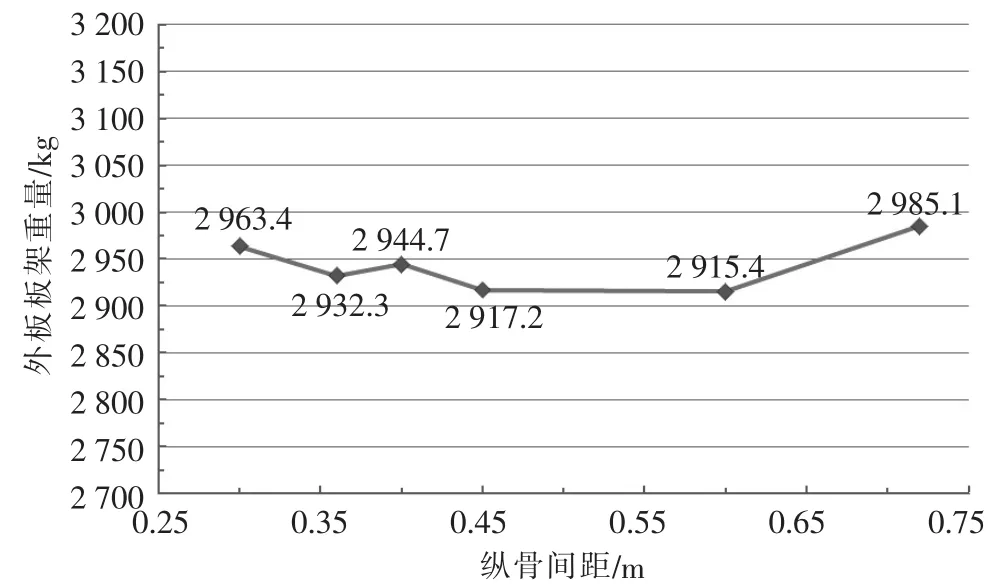
图2 不同纵骨间距下外板板架的质量情况

3 冰区舷侧结构非线性有限元分析

从上分析可以看出纵骨间距为450 mm和600 mm的结构质量最小且相差不大。根据芬兰海事局（Finnish Maritime Administration，FMA） 出版的纵骨架势船体结构直接强度计算的指南文件，可以通过一种高级的分析方法，即非线性有限元方法，来分析在极限冰压情况下，舷侧纵骨的塑性变形［5］，从而决定采用哪一种布置。两种需要计算的舷侧结构尺寸如表6所示。

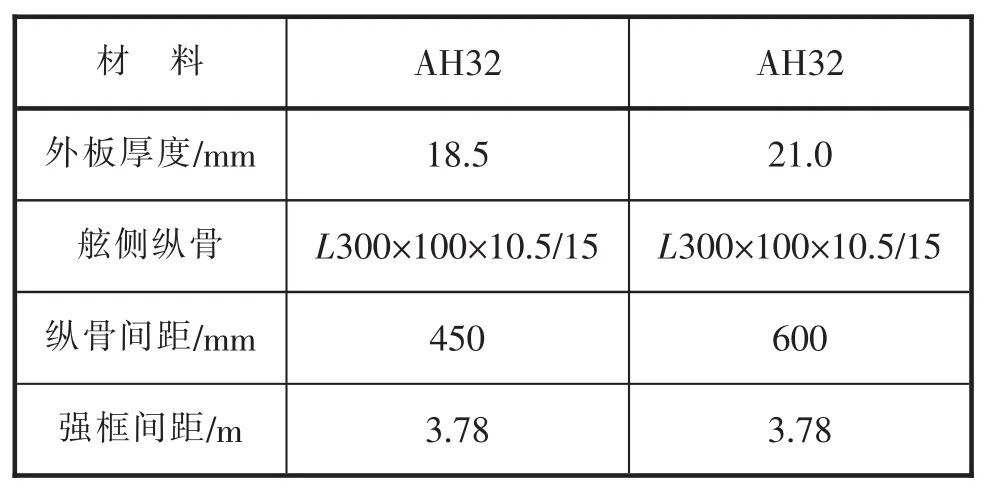
表6 舷侧结构尺寸

3.1 有限元模型范围

舷侧结构有限元模型的范围包括纵向、横向和垂向。

1）纵向包括最少三个强框架，在前后端再延伸出半个强框架；

2）横向包括整个双壳结构；

3）垂向位于冰带内的两个水平桁材之间。

3.2 单元网格

有限元模型中使用板单元（Shell Element）来模拟外板、内壳、强框以及冰带范围内的纵骨。梁单元（Beam Element）用来模拟冰带范围外的纵骨。冰带范围内的纵骨的面板也用板单元建模。

由于要进行非线性有限元分析，所以在冰带范围内的结构要保持一定的网格密度，即用细化网格建模。通常冰带内的纵骨腹板应不少于3个单元，面板应至少为1个单元。冰带区域内的外板和强框保持与纵骨相同的网格密度，冰带区域外的结构可以用较粗的网格模拟，但要做好从细网格到粗网格的过渡。

3.3 材料模型

当材料达到屈服极限以后，材料的非线性关系源于应力和应变的非线性关系。在计算中，通常需要设定一个应力应变关系曲线来模拟材料在屈服之后的行为。在本文的计算中采用理想弹塑性材料模型，不考虑应变刚化效应，因为这样的简化能得到较为保守的结果。

由于船体结构均采用高强度钢AH32，故理想弹塑性材料模型的主要参数如下。

1）屈服应力315 MPa；

2）杨氏模量206010 MPa；

3）泊松比 0.3。

分析的有限元模型如图3～5所示。在冰带区域中间位置的纵骨用“B”标识，它邻近的纵骨用“A”和“C”标识。

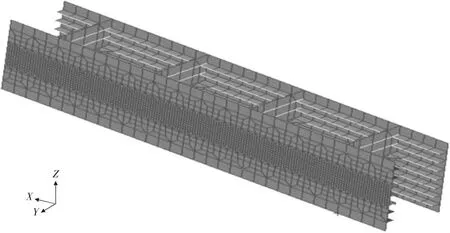
图3 有限元模型

图4 外板和舷侧纵骨

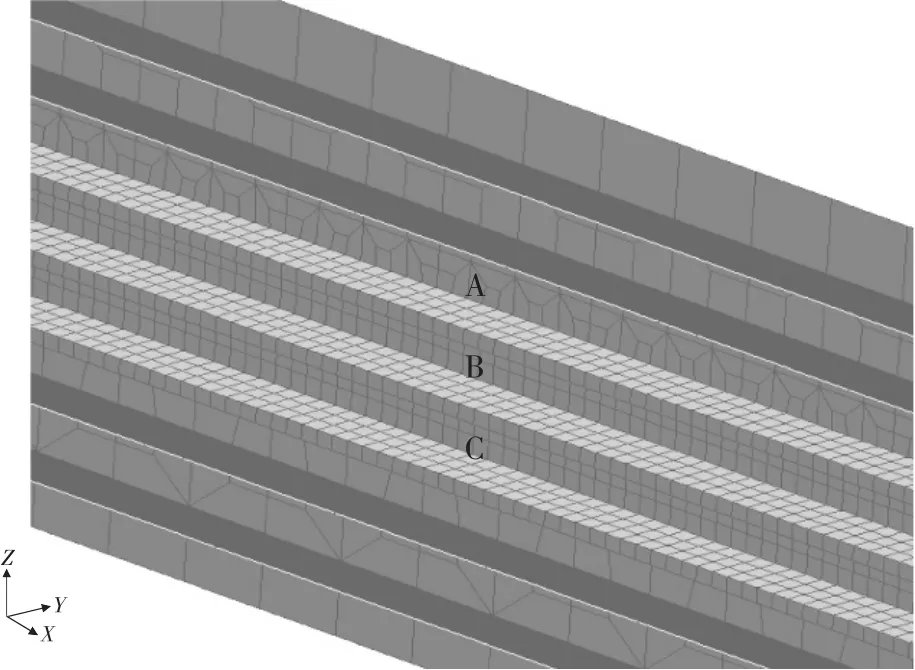
图5 舷侧纵骨细节

3.4 边界条件

模型的边界条件如图6和表7所示。

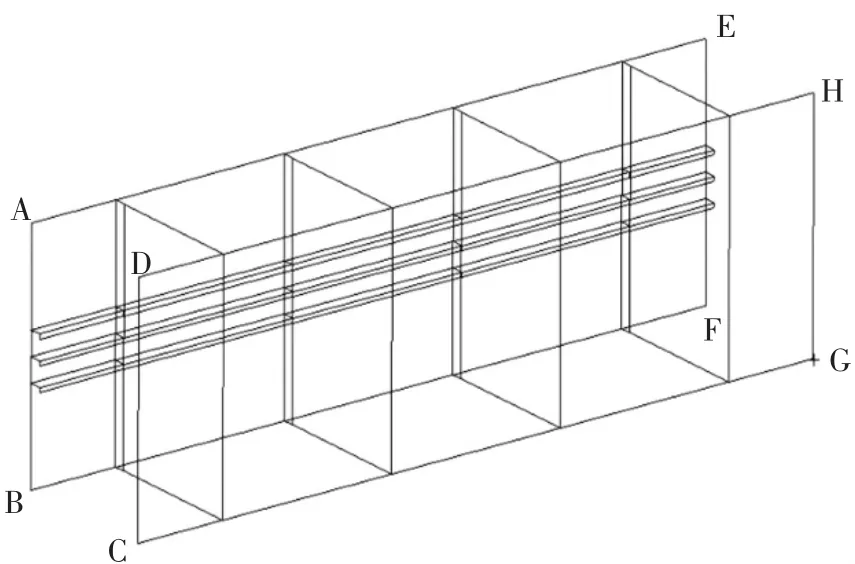
图6 模型的边界条件

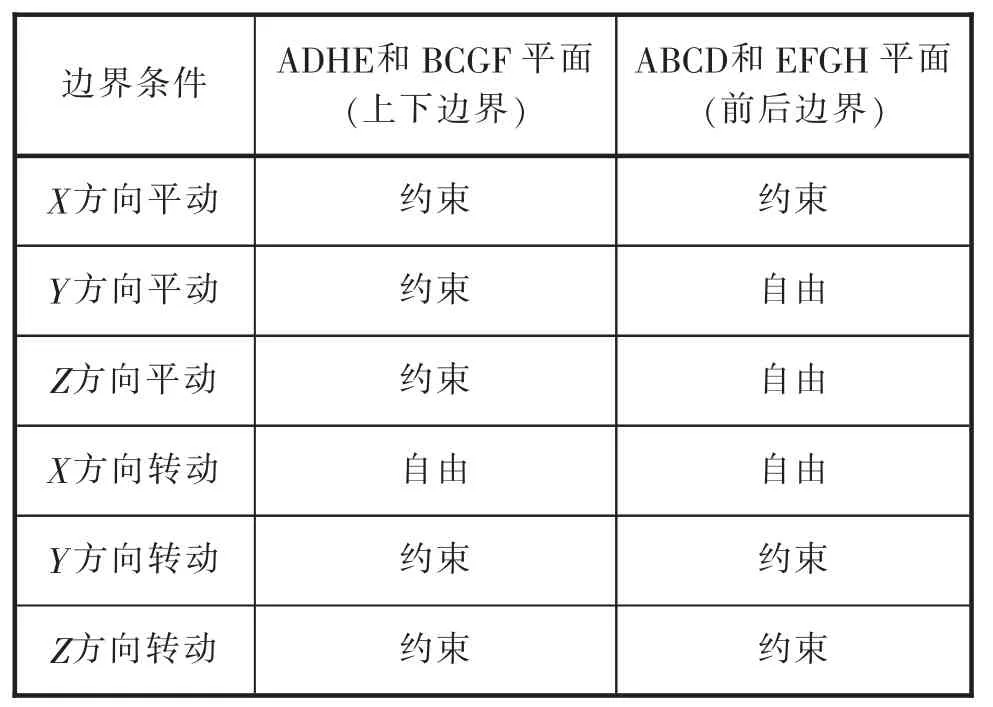
表7 模型的边界条件

上下边界的所有平动自由度全部被约束，允许X轴方向的转动，模拟上下边界水平桁材的刚度。

前后边界上施加了一个关于X轴方向的对称边界条件，模拟结构在X轴方向上是连续的。

3.5 施加在舷侧纵骨上的载荷

根据FMA指南，极限冰压pmax的公式如式（5）：

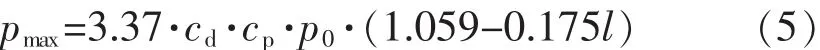
得出极限冰压pmax，需要转化为线载荷施加在有限元模型中冰带范围内的舷侧纵骨上。

图7表示了非线性有限元分析过程中的载荷加载和卸载的过程，载荷逐渐增加到最大值，然后再逐渐减小到0。

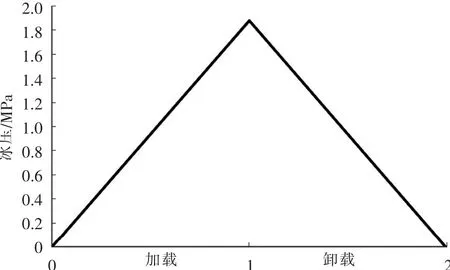
图7 载荷加载过程

3.6 非线性有限元计算结果

非线性有限元分析利用商用有限元软件MSC.Marc，采用自适应方法（Adaptive）和 Full Newton-Raphson迭代方法对模型进行分析。

分析后可以得到两种纵骨间距下，冰带区域纵骨B的载荷变形关系曲线，如图8所示。

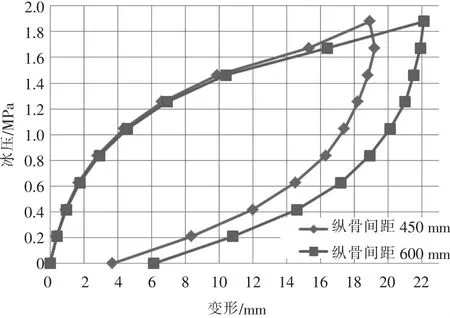
图8 两种间距下纵骨B的载荷变形关系曲线

从图8可以看出，纵骨间距为600 mm结构的永久塑性变形要大于纵骨间距为450 mm结构的永久塑性变形。

4 结语

本文根据意大利船级社钢质海船规范、芬兰海事局的冰级规范及相关指南文件，对一艘冰级符号为IB的成品油船的舷侧结构进行了不同纵骨间距情况下的优化分析。

在满足规范要求的前提下，从外板板架质量分布的情况可以看出，并不是纵骨间距越大越好或者是越小越好，而是存在一个中间值，使得外板和纵骨的组合恰到好处。

本文利用非线性有限元方法分析了质量最小的两种纵骨间距情况下，纵骨在极限冰压作用下的塑性变形情况。可以看出，由于两种情况下的纵骨尺寸相同，只有纵骨间距和外板厚度不同，所以得出的结果是间距为600 mm的纵骨塑性变形大于间距为450 mm的纵骨塑性变形。然而采用较大纵骨间距的结构（600 mm）可以减少结构质量和焊接工作，从而降低生产成本。这需要设计方进行综合考虑。同时，非线性有限元方法为结构的优化设计提供了手段，为具有冰级符号的船舶设计提供了一种新的思路。