应用改进遗传算法解决武器目标分配问题

闫玉铎

摘要：在实际作战过程中，以当前战场态势为输入，特定交战规则为约束的武器目标分配（Weapon Target Assignment，WTA）问题是指挥员必要的决策行为之一。因此，在作战仿真系统中，WTA模型是计算机生成兵力（Computer Generated Forces，CGF）决策行为模型的重要组成部分。对WTA进行有效建模有助于提升决策行为模型的逼真性与智能性，以及仿真结果的可信性和有效性。本文主要研究WTA决策行为建模与优化求解问题，主要包括WTA模型建立，以及面向高实时、高可靠性实际应用需求的算法。论文的最后，通过设计对比实验，验证了WTA模型及提出的改进遗传算法的可行性与有效性。

关键词：武器目标分配;建模与优化求解;改进遗传算法

中图分类号：TP391.9    文献标识码：A  文章编号：1007-9416（2018）10-0000-00

1 引言

在真實的战场环境下，WTA问题是指在对敌我双方当前战场态势的获取与分析下，针对我方多个装备同类型武器的作战单元与多个敌方威胁目标，如何把我方具有不同杀伤力的武器及时合理地分配，构成整体优化的火力打击体系。

WTA问题是一个多参数、多约束的不确定性多项式完全问题[1]。该问题本质上需要依靠完全列举法来找到优化方法。但随着作战规模的不断增加，其问题的解空间以指数方式上升，并呈现出组合爆炸的趋势。从是否考虑时间因素的角度，WTA问题的模型研究又可分为静态WTA（Static Weapon Target Assignment， SWTA）模型与动态WTA（Dynamic Weapon Target Assignment， DWTA）模型研究。静态的WTA基础模型如公式（1）所示。现阶段绝大多数的研究都是以此模型作为基础。在模型中，M表示我方的武器平台种类数，N表示敌方的目标数，W表示敌方目标的威胁值，p表示我方武器对敌方目标的击毁概率，x表示武器目标分配方案，为优化函数的自变量，F（x）为此优化函数的优化目标，表示我方武器对目标威胁的打击效果，F（x）越大，表示对敌方的打击效果越好。

   （1）

2 相关工作

最初，解决WTA问题的方法是基于线性规划，动态规划，图论这些传统算法。在20世纪80年代中期，WTA问题已被证明是一个NP完全问题，这意味着任何确定性算法不能获得在多项式空间的最优解。

20世纪90年代初以来，国防分析研究所（IDA）一直在研究WTA问题，在这期间他们改进了武器的优化和资源需求模型（WORRDM）[2]。现代战争中，随着C4ISR的广泛应用，IDA提出对WORRDM模型的进一步改进策略，进而建立C4ISR环境下的作战资源分配模型（Engagement Resources Allocation Model，ERAM）。余家祥等[3]针对舰艇编队内多型区域防空武器抗击来袭导弹的WTA问题展开研究;王波等[4]以反舰导弹打击敌水面舰船为背景，并应用改进的遗传算法进行求解;韩松臣等[5]对WTA问题进行描述并提出了基于马尔可夫决策过程解决动态问题的方法，该方法中将动态的分配策略与静态模型相结合以求在作战中对武器进行动态分配。崔莉莉[6]以蚁群算法的信息更新规则为基础，引入PSO算法中的利用搜索经验对后续粒子群的指导机制。此方法经过实验验证有效扩展了群体的搜索空间，同时对算法效率也有所提高。

3 WTA模型建立

3.1 WTA概念模型的建立

建立WTA模型，要优化的目标包括对我方的资源保存值和对敌方目标威胁的损伤值。

首先建立WTA概念模型，我们的武器概念模型可以表示为：

m表示我方武器平台的个数，同一武器平台中的武器种类相同，表示第i个武器平台拥有武器的数量为。

目标的概念模型如下建立：

n表示敌方目标的总数，表示敌方第j个目标。

武器分配计划的概念模型如下建立：

表示使用个武器平台i中的武器来打击目标j，这里有。

3.2 WTA数学模型的建立

在本文中的WTA问题，目标是在损伤最少的资源以及给敌人的目标威胁造成最大的伤害。因此，我们建立优化目标H（x），以尽量减少敌人的目标威胁程度同时最大限度地保存我方的资源。建立WTA优化模型：

    （2）

（3）

下面对模型中的变量与参数加以解释说明：

如上数学模型中所示，F（x）代表对敌方目标威胁的损伤程度;G（x）代表对我方资源的保存程度;优化目标H（x）=aF（x）+bG（x）综合考虑了损伤敌人的目标威胁程度同时提高我们保存的资源保存程度，a和b由指挥员很据战斗的具体目标设定，不同的值反映指挥员对战斗目标的不同要求，a+b=1，。特殊的，a=0，b=1表示此次作战行动以最大程度保存我方资源为战斗目标;a=1，b=0表示此次作战行动以最大程度打击敌方威胁为战斗目标。

模型中，我方武器集合用矩阵表示，其中表示我方第i个武器平台拥有武器的数量，m表示我方武器平台的种类数量，我方拥有的武器总数为。在进行武器目标分配中，使用同一种武器对目标打击的数量总和不能超过该武器平台的数量上限，由此建立分配的容量约束：

为了保证对于某一敌方目标我方可以分配足够的武器进行打击而又没有武器的过度浪费，模型中引入策略约束，其中表示在正常状态下我方武器i成功将目标j摧毁的概率。此约束表示对于某一目标j，我方对其进行打击的武器总的摧毁概率不超过99%，以实现武器的合理分配。

我方资源值用矩阵表示，表示我方第i个资源的价值，l表示我方资源的总数;敌方目标威胁值用矩阵表示，表示敌方第j个目标的威胁值。我方资源与敌方目标威胁的取值均在0到1之间，表示我方每个资源价值占总价值的比例以及敌方每个目标威胁所占的比例，这两个取值由战场指挥员根据作战进程进行评估。

模型中对于武器状态建立状态矩阵，其中表示我方第i个武器平台的状态向量，表示为：，表示第i个武器平台中第k个武器的状态，取值越大，表示该武器的保存状态越好，模型中为了方便处理，模型中取或，分别表示该武器已经被摧毁或保存完好。

建立通视矩阵表示，该矩阵为三维矩阵，表示第i个武器平台中第k个武器与目标j之间的通视性，通视性对武器与目标之间的发现概率与打击概率都有所影响，在本文中对发现概率与打击概率综合考虑，均由通视性因子表示。前文已经提到，在真实战场环境下，武器与目标之间的通视性由多方面因素影响。在本模型中，主要考虑武器与目标所处的地形条件与气象条件两方面因素，并建立相应的影响因子，并有。

4 WTA求解算法

4.1传统遗传算法求解

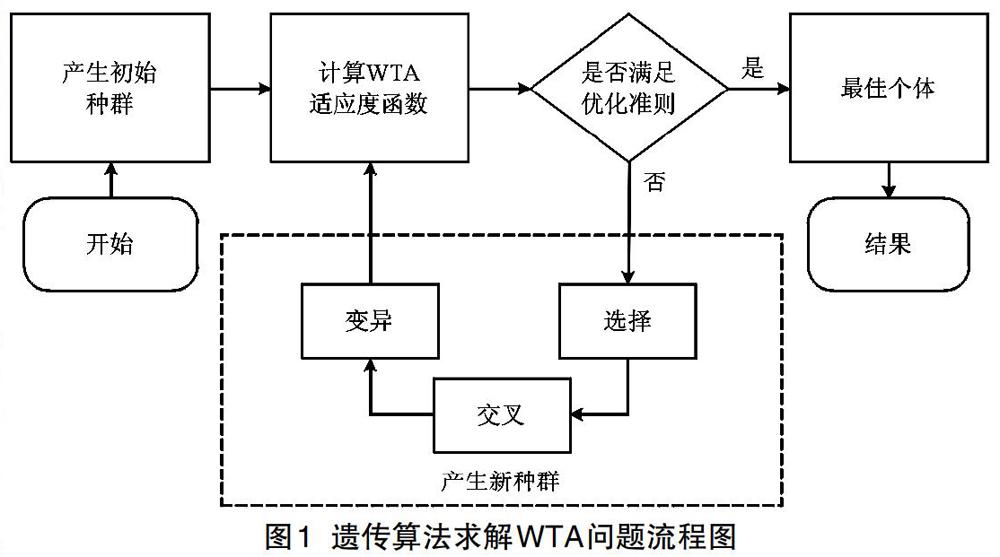
遗传算法为求解复杂系统优化问题提供了一种通用框架，它不依赖于问题的实际意义与应用背景。对于本文中需要解决的WTA优化问题，其求解的流程如图1所示。

第1步：随机产生初始种群，种群大小一定，将每个群体中的个体以染色体的基因编码的形式表现出来;

第2步：对种群中所有个体在WTA问题中的适应度函数值进行计算，并判断结果是否满足优化准则，若满足，则将该个体及其代表的最优解输出，结束计算，若不符合则执行第3步;

第3步：根据适应度函数值的大小选择进入子代的个体，适应度函数值高的个体被选中的机会较高，适应度低的个体更容易被淘汰;

第4步：按照设定的交叉概率和交叉操作方法，产生新的个体;

第5步：按照设定的变异概率和变异操作方法，产生新的个体;

第6步：将交叉和变异产生的新一代个体组成新一代种群，执行第2步。

遗传算法中的优化准则：不同问题的有不同的优化准则。本文研究的优化问题中所采用的优化准则为遗传迭代次数是否超过预先设定值。

4.2传统遗传算法的局限性

遗传算法这样的衍生进化类算法采用随机搜索机理，积累成千上万代正向的有积极意义的进化方能得到卓有成效的改进[7]。这是对实时性有较高要求的WTA问题所不能接受的弊端。

遗传算法在每次迭代过程中，选择、交叉和变异的操作是盲目的[8]，这是算法的机理问题。这也直接导致了遗传算法在求解过程中效率较低、收敛较慢。同时，传统遗传算法在收敛过程中容易陷入局部最优而出现过早收敛，它使得种群演化到非全局最优状态，进一步迭代已不能产生更佳可行解。

鉴于遗传算法存在这样的不足，众多文献在解决WTA问题这样类似的实时性很强的优化问题会选择启发式寻优的遗传算法和一些具有指引性的智能算法相结合的遗传算法改进策略，以抑制其盲目尋优和过早收敛的局限性。

4.3改进遗传算法

差分进化算法是一种效率较高的进化搜索算法，其原理和结构类似于遗传算法，同样采用遗传操作（选择、交叉和变异）。差分进化算法在实际优化问题中能够表现出色，原因有两点：首先，差分进化算法将一部分个体的差分信息作为扰动量，使算法在跳跃距离和搜索方向上具有自适应性，从而改善了遗传算法变异和交叉的盲目性;其次，1V1竞争机制使得进化过程中，整个种群的质量逐步提升，拒绝了遗传算法盲目选择导致的质量较差的部分个体迟迟不能淘汰，从而阻碍种群的进化[9]。

针对遗传算法盲目的随机寻优和过早收敛，为了平衡计算代价和解的精度，在不追求解全局最优且寻优时间有限的情况下，本文基于遗传算法给出了针对性的算法改进策略，引入了差分进化算法的1V1竞争机制和差分变异机制以及粒子群算法的更新规则，以期最大程度的克服其盲目寻优和过早收敛的缺陷。具体的本文提出的改进遗传算法的流程图如图2所述。

如2所示，本文提出的改进遗传算法基本保存了传统遗传算法的运算流程，不同的是，在更新种群的环节，本文引入了差分变异与粒子群算法的更新规则产生新的种群并与原传统遗传算法产生的种群进行1V1竞争，这种方法虽然在时间消耗上有一定损失，但是可以有效地避免传统遗传算法盲目寻优造成的收敛过慢以及样本多样性不足造成的陷入局部极小。

5 实验及结果

为验证本文提出的改进遗传算法的性能改进效果，基于实际WTA问题的数学模型，采用本文提出的改进遗传算法、差分进化算法和传统遗传算法分别进行测试，测试的数据与前文的获取方法相同，首先设计一个简单的实验案例，案例中，模型的参数通过人为进行设定，通过设定武器和目标数量m和n的值来设定不同的作战规模，模型中其他参数由计算机随机生成。在本节的对比实验中，为了将不同的智能算法求解效果进行对比，在进行同一组对比实验中使用的数据是相同的，以下是具体的测试结果。我们基于m，n=5，m，n=10，m，n=15，m，n=20，m，n=25，m，n=30，m，n=35这7种不同作战规模下各做了10次实验，以分析在不同作战规模下，传统的遗传算法、差分进化算法和本文提出的改进遗传算法的性能，这里主要分析算法的适应度函数收敛情况和算法的实际运行时间。适应度函数收敛情况主要表现于算法达到收敛或最大迭代次数时的适应度函数值;算法的实际运行时间体主要表现于算法达到收敛状态或者达到最大迭代次数的运行时间。本实验中，将迭代次数设定为100。

由于实验结果数据量大，为了对实验结果有更直观的展示，现将7种作战规模下，三种智能算法的适应度函数收敛情况和算法的实际运行时间数据分布情况通过箱线图来进行展示，如图3和图4所示。

在图中，红色的线表示数据中位数，箱子的上下边缘分别表示数据的3/4和1/4分位数，箱子两头的延伸线表示数据的最大值和最小值，离散的点表示统计意义上的异常值。通过箱线图，我们可以非常直观的看到不同算法适应度和实际运行时间上的数据分布，且由图中可明显看出看，本文所提出的改进的遗传算法在适应度收敛情况方面表现明显优于其他职能算法，且收敛能力极为稳定。在运行时间方面，虽然略高于其他算法，但是仍处于一个量级上，并无明显差异。

为了进一步分析，我们在三种算法适应度函数收敛情况和算法的实际运行时间数据上进行的简单的统计分析在原始数据上，分别对7种作战规模的10次试验结果的最优结果，最劣结果，平均情况，中位数以及标准差进行统计，由于其包含的数据量较大，在此我们对其中包含的较有价值的信息进行进一步分析。均值和标准差是反映数据整体特征的重要指标，故我们针对三种算法在不同作战规模下的适应度函数收敛值和实际运行时间的均值和标准差进行可视化处理，如图5和图6所示。

从图中可知，本文提出的改进遗传算法适应度函数的收敛效果十分理想，且收敛情况十分稳定，基本没出现达不到收敛状态的情况，对比之下，差分进化算法和传统遗传算法的收敛情况都不是十分理想且远差于改进遗传算法，并且两者的算法性能发挥都十分不稳定，收敛情况波动较大。在算法实际运行时间方面，三种算法都处于一个量级，尽管图中显示传统遗传算法的运行时间是最短的，但在实验所设定的100次迭代次数中，由表4.4可知，在规模较大的情况下，传统遗传算法有相当一部分实验中，算法最终没有达到收敛，因此图中显示的运行时间并不能完全说明改进遗传算法的效率较差，在规模较小的情况下，尽管改进遗传算法较传统遗传算法消耗时间更多，但是在真实的战场环境下，为了获得更好的武器目标分配结果而消耗的少量时间代价，是完全可以接受的。

在分析了不同作战规模下，三种智能算法的性能分析之后，本文提出的改进遗传算法体现了明显的优势。故我们认为，在实际应用过程中，本文提出的方法是非常有竞争力的。

6 结语

在本文中，我们首先建立WTA数学模型，进而对遗传算法解决WTA问题的求解流程进行介绍，并分析其求解过程中存在的不足，针对于遗传算法的盲目搜索与易于陷入局部极值两个问题，本文引入了差分进化算法的1V1竞争机制和差分变异机制以及粒子群算法的更新规则，提出解决WTA问题的改进遗传算法，并通过实验验证了本文提出的改进遗传算法具有快速且稳定的算法性能与较高的适用性。

参考文献

[1]Lloyd S P， Witsenhausen H S. Weapons Allocation is NP-Complete[C]// IEEE Summer Conference on Simulation. 1986.

[2]Koleszar G E， Bexfield J N， Miercort F A. A Description of the Weapon Optimization and Resource Requirements Model （WORRM）[J]. A Description of the Weapon Optimization & Resource Requirements Model，1999.

[3]余家祥，赵晓哲，史红权等.基于遗传算法的编队区域防空武器分配方法[J].现代防御技术，2013，41（1）：82-87.

[4]王波，刘小利，胡亮等.基于改进遗传算法的反舰导弹火力分配研究[J].火力与指挥控制，2015，40（8）：90-93.

[5]韩松臣.导弹武器系统效能分析的随机理论方法[M].国防工业出版社，2001.

[6]崔莉莉.基于蚁群算法的武器-目标分配问题研究[D].上海：上海交通大學，2011.

[7]徐宗本，高勇.遗传算法过早收敛现象的特征分析及其预防[J].中国科学：技术科学， 1996，（4）：364-375.

[8]何大阔，王福利.一种提高遗传算法全局收敛性的方法[J].东北大学学报（自然科学版），2003， 24（6）：511-514.

[9]林川.粒子群优化与差分进化算法研究及其应用[D].西南交通大学，2009.

An Improved Genetic Algorithm for Solving Weapon Target Assignment Problems

YAN  Yu-duo

（PLA Unit 31002， Beijing  100094）

Abstract： During the actual combat， the Weapon Target Assignment （WTA） problems， with the real-time battlefield condition as input and specific combating engagement rules as constraints， is one of the necessary decision-making behaviors of the commander. Therefore， in the combat simulation system， the WTA model constitutes an important part of the Computer Generated Forces （CGF） decision behavior model. Effective modeling of WTA contributes to improve the intelligence and facticity of decision-making behavior models， as well as the effectiveness and credibility of simulation results. In this paper， the modeling and optimizing solution problem of WTA decision behavior were mainly studied， including the establishment of WTA model and the algorithm for high-real-time and high-reliability application requirements. At the end of the paper， the feasibility and effectiveness of the WTA model and the proposed improved genetic algorithm are verified by designing comparison experiments.

Keywords：Weapon Target Assignment （WTA）; modeling and optimizing solution; improved genetic algorithm