基于BP神经网络的隧道位移反分析方法研究
边 睿
(山西省交通科学研究院,山西 太原 030006)
0 引言
随着现代支护结构理论的发展与隧道科学技术的进步,目前普遍认为,隧道是包含荷载、结构、材料三者于一体的构造物,同时,基于新奥法而设计的复合式衬砌俨然已成为主流隧道衬砌方式。其中,隧道围岩一方面作为隧道客观形成条件而存在,另一方面也作为重要的支护结构参与隧道的变形协调与受力平衡。然而,由于隧道围岩是天然形成,且由于地质环境的多样性、复杂性,测定围岩参数十分困难,同时,由于岩土勘察方法的局限性导致隧道围岩参数难以准确测量,这就为合理设计隧道支护参数增加了难度,也变相降低了隧道稳定性与可靠度。寻求可靠的围岩参数测量与计算方法对于隧道设计与建设有十分重要的意义。
人工神经网络(ANN)具有高度非线性,可自我学习、自我组织与一定思维、意识等特点。根据已知的数据、理论、方法等去分析和解决未知的问题,在工程应用中有重要的意义。BP算法[1]即为Rumelhart等人提出的误差反向传播训练算法,BP算法在工程参数反演过程中已有了广泛的应用。
在现有的岩土工程理论与工程实际应用中,岩土结构的相互作用与自身受力原理研究尚不清晰。传统的数值模拟方法与力学解析方法都难以说明各结构层对于位移的影响[2]。BP人工神经网络参数反演分析,是以工程类比法为背景,通过神经网络位移反分析得到围岩相关参数的方法。由于神经网络的特殊性,在反演分析的过程中无需再考虑力学作用原理,利用BP算法强大的函数非线性运算能力,结合准确的样本分析,即可进行反演分析,得到围岩参数的相关数据。
1 BP神经网络原理
BP神经网络是以误差逆向传播算法为运行方法的多层前向神经网络,以其优秀的函数映射与分类模式能力而著称,常用于处理XOR等问题。
误差逆向传播算法以系统的误差平方和最小值为标准,通过该算法的逆向传播不断地修改网络结构的参数,计算系统误差平方和,直至达到误差平方和最小的目的。其网络结构模型包含输入层、隐含层和输出层3个层次。

图1 BP神经网络拓扑图
此算法包括信息正向传播和误差反向传播两个过程,3个结构层次的神经元分别负责信息和数控的输入,处理变换和输出处理结果。隐含层作为中间层,担负着信息的处理变换功能,可以根据数据与精度等要求将其设计为单层或多层。一个完整的信息输入、变换及输出则完成一次信息的正向传播,当输出结果与预期有差距时,开始进行误差反向传播,由原来的路径进行反向传播,逐层调整变换各层次之间的权重。往复循环,不断地进行正向与反向的过程,不断地调整权值,直至达到误差所规定误差范围抑或达到设定的训练次数。
当用Matlab实现BP神经网络时,其大致流程有以下几个步骤[3]:
a)确定神经网络结构层参数。
b)准备训练样本。
c)使用Matlab工具箱创建,训练网络。
d)进行反演分析。
2 工程应用实例
2.1 工程概况
草城沟隧道位于岢岚县高家会乡草城村西,设计为左右线分离式,右洞全长2 955 m,左洞全长2 916 m,左右线均属长隧道。隧道总体走向呈235°,隧址区范围内出露地层由老到新为寒武系三山子组(∈3s)、第三系上新统静乐组(N2j)、第四系上更新统马兰组(Q3m)地层。钻孔中未见地下水。
隧道采用复合式衬砌。隧道初期支护参数为:喷射C25混凝土,厚26 cm;20-a型钢架,纵向间距60 cm;φ6钢筋网,20 cm×20 cm;D25 mm中空注浆锚杆系统锚杆,长3.5 m,间距100 cm×80 cm。
2.2 确定神经网络结构参数
合理确定BP网络结构层参数,是关系到网络功能要求、误差精度、训练速度等问题的关键点[4]。
2.2.1 输入层
样本包含的内容决定输入层神经元的内容。在实际的隧道工程中,一般会对隧道的变形、围岩压力等进行监控,可选取上述参数作为输入层参数。在本例中,选取隧道变形监测值作为输入层参数,即周边收敛值和拱顶沉降值。
2.2.2 输出层
输出层即为反演分析的目标参数。隧道工程问题是集地质学、岩土力学、结构力学和岩石力学于一体的复杂问题。隧道的稳定性不同程度地受到围岩力学参数良好与否、地下水繁育情况、施工工艺水平高低、施工方法的选择合理与否等方面的影响。结合工程勘察和设计实践的实际情况,一般认为围岩力学参数是影响隧道稳定性的关键因素。围岩力学参数是否准确将直接影响隧道结构计算准确性。在本例中,选取围岩的弹性模量E、黏聚力C和内摩擦角φ作为反演输出层节点。
2.2.3 隐含层
隐含层参数包括隐含层层数和隐含层节点数。隐含层层数越高网络结构越复杂,训练时间越长,一般通过将隐含层层数设置较低,节点数设置较高来达到快速训练,保证精度的要求。基于此,本例中将隐含层层数设置为1,隐含层节点数设置为12。
2.2.4 其他结构参数确定
本文中训练算法TRANLM算法;隐含层传输函数为对数传递,输入层和输出层为线性传递。
2.3 准备样本
反演分析的数据样本由数值模拟结果得出。上述分析中,将弹性模量E、黏聚力C和内摩擦角φ作为研究对象,样本的准备将以这4个参数作为基准进行样本正交试验设计,按照试验设计结果,进行数值模拟,将得到的数值模拟结果作为训练样本。
正交试验是利用正交表安排试验,将多因素多变量合理组合出部分具有代表性的试验进行研究,以期通过这部分试验了解全面试验的情况。此种方法高效、快速、经济,避免了全面试验的繁复。
结合公路隧道设计细则中对Ⅴ级土质围岩物理参数的规定,弹性模量E的取值区间为5~30 MPa,黏聚力C的取值区间为15~60 kPa,内摩擦角φ的取值区间为15°~30°。根据正交试验的设计要求,参数选取如表1,实验安排及结果如表2。
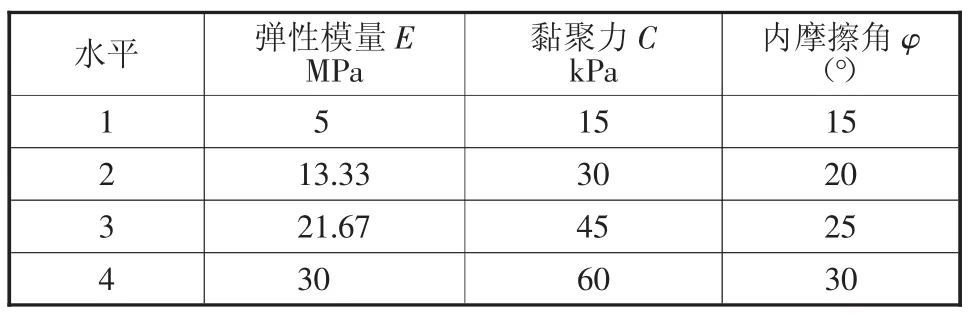
表1 试验设计水平表[5]

表2 试验结果表
根据工程实际,取某断面作为典型断面,构建数值模拟模型,取拱顶沉降值与周边收敛为监测对象。隧道埋深30 m,依据圣维南原理,将模型设置为宽120 m,下部深度40 m,纵向深度20 m。边界条件为控制x方向边界的x位移,y方向边界的y位移,下边界控制z位移,模型围岩简化为均值各向同性,本构关系符合摩尔库伦准则,围岩初始应力考虑自重应力。隧道开挖采用两台阶法,锚喷支护,其设置参数与工程实际一致。数值模型示意图与锚喷支护效果图如图2。

图2 数值模型示意图与锚喷支护效果图
围岩重度 γ=17.71 kN/m3,泊松比 μ=0.31,其余参数取自正交试验设计方案;锚杆与初支的材料参数结合工程数据,具体取值如表3,数值模拟结果如表2。

表3 材料参数选取表
2.4 围岩参数反演分析
将训练样本进行归一化处理后输入神经网络Matlab 计算程序(newff:前馈网络创建函数;train:训练一个神经网络;sim:使用网络进行仿真),输入层节点数a=3;隐含层层数为1,节点数n=12,学习速率为0.001,输出层节点数b=2。计算精度设置为10-4,最大训练次数5 000次。
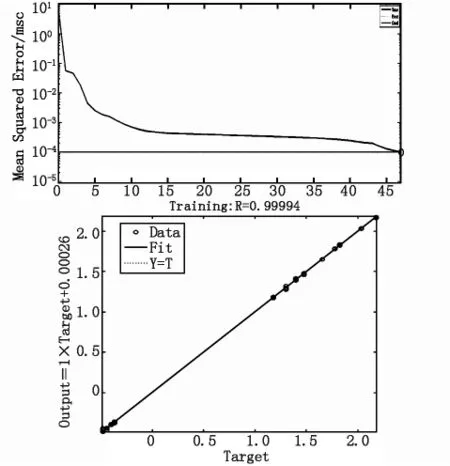
图3 训练性能图与相关性图
从图3中可以看出,网络收敛性能好,且相关性极好。
将工程实地测量的断面数据写入完成训练的BP神经网络模型中,得出位移反演分析结果,以得到的围岩力学参数作为数值模拟参数进行模拟,可得到各断面的位移数据,如表4所示。

表4 反分析与数值模拟结果对比表
对比数据,数值模拟分析结果与实际测量值基本一致,间接证明了此次反演分析网络结构的可靠性。
3 结论
本文通过设置合理的神经网络结构参数,以正交试验设计为方法,数值模拟为手段,取得合理有效的BP神经网络反演模型,基于BP神经网络的隧道位移反分析方法针对围岩的物理参数进行了分析研究,将反分析结果代入数值模拟正分析程序,验证了BP神经网络的隧道位移反分析方法的准确性与可靠性。
对于大多土木工程而言,精准地对地质环境进行勘察在实际工程中难以实现,往往受到预算过大、干扰严重、设备落后、测点数量等限制,在设计阶段大多采用工程类比方法得到某区域的平均建议值。如果将位移反演分析结论与地质勘察成果相结合,对围岩性质等目标参数进行优化调整,则对于隧道支护参数设计有实际意义,有助于进一步加强隧道稳定性。

