跳跃风险、经济不确定性指数及其波动与趋势特质分析

沙楠

摘要：方差风险溢价作为度量经济不确定性的代理变量，对未来多期超额收益率具有显著的预测能力。将方差风险溢价拆分为趋势项和波动项，发现两者的作用区间存在显著差异：短期内波动项起主导作用，中长期内则趋势项起主导作用。拆分后整体的预测效果有显著提升。在分析趋势项和波动项的性质时，引入了正负跳跃风险作为控制变量。研究发现，正负跳跃风险的预测能力存在显著的非对称性，负跳跃风险的预测能力较强，而正跳跃风险的预测能力较弱。

关键词：方差风险溢价；已实现方差；隐含方差；跳跃风险

文献标识码：A文章编号：100228482018（01）007410

一、 问题的提出

学术界存在很多度量宏观经济不确定性的指标，如Manela和Moreira[1]利用《华尔街日报》头版文章的历史数据构造了新闻中隐含波动率指数，Baker、Bloom和Davis[2]根据报纸报道的频率构建了经济政策不确定性指数（Economic Policy Uncertainty，EPU），Bollerslev、Tauchen和Zhou[3]利用股市高频数据计算出了方差风险溢价（Variance Risk Premia，VRP）等。与前两种文本构建方法得出的指标不同，VRP直接取自股市交易数据。股市在一定程度上是宏观经济的晴雨表，因此取自股市的VRP可以有效反映宏观经济的不确定性。此外，已有研究发现该指标与货币政策、石油价格及金融系统不稳定指数（CISS Index）具有紧密的联系[4]。

在数值上，VRP等于隐含方差（Implied Variance，IV）与已实现方差（Realized Variance，RV）的期望值之差，用以度量方差在两种概率测度下的溢价水平。其中，已实现方差是利用高频数据加总计算而得的，在股票市场中抽样时间间隔多为5分钟，在外汇市场中抽样时间间隔多为15分钟。隐含方差可利用方差互换数据（场外市场）或期权数据（交易所）计算得出。与RV和IV相比，VRP包含了更多信息，且在绝大多数月份内为正值[56]。研究发现，VRP对未来多期超额收益率具有显著的预测能力，且预测效果在短期内（4个月左右）达到最优[7]。此外，VRP与其他高阶矩风险溢价（相关性风险溢价、偏度风险溢价及峰度风险溢价等）的联系也较为紧密。

既然VRP可作为宏观经济不确定性的代理变量，那么在整体的不确定性中波动项和趋势项的作用机制是否存在差别是本文研究的第一个问题。若进一步将其细分，已实现方差的波动项、趋势项与隐含方差的波动项、趋势项各自又在其中起什么作用是本文研究的第二个问题。股票价格除扩散风险外，还存在着跳跃风险，此时若进一步引入二阶矩的正负跳跃风险项，趋势项和波动项是否依然可以保持显著是本文关注的第三个问题。本文的创新之处有两点：第一，通过对方差风险溢价的拆分有效提高了对多期超额收益率的预测效果；第二，通过对跳跃风险的拆分有效识别了正负跳跃风险项的非对称性预测机制。

二、 文献回顾

国外学者对VRP理论基础和定价应用的研究较为全面。理论框架主要有长期风险模型（Long Run Risk Model）、资产定价各种定价核（Kernel）[8]以及累积前景理论[9]等。在场外市场（OTC）数据日益丰富后，从方差互换合约中隐含方差期限结构推导出的无套利模型则是最新的研究成果[10]。定价应用层面多从时间序列和横截面角度展开分析，有学者将VRP与宏观经济变量进行了相关性分析，也有学者将VRP作为风险因子，使用FamaMacbeth方法对股票进行排序分组，并研究此定价因子的显著性。本文从理论基础和定价应用两个层面对相关研究文献进行梳理。

（一）理论基础

对多种高阶矩溢价的理论模型，可按各自特点将其划分为三类：第一，从消费资本资产定价模型发展而来的长期风险模型，其理论基础最为完善；第二，从行为金融理论衍生出来的累积前景模型，其理论框架自成体系；第三，从实际场外交易数据推导得出的无套利模型，其理论基础稍微薄弱。

1.长期风险模型

长期风险模型认为经济中存在一个关键的长期风险项，通过引入三个状态变量（消费增长率、股利增长率及方差项），并结合对数线性化的方式求解出消费财富比率、市场收益率及无风险收益率等。在合理的参数设置下，该模型可以较好拟合实际经济的特征[11]。长期风险模型假设投资者的效用函数满足EpsteinZin形式，此效用函数的设定使投资者偏好于提前对冲掉不确定性，为避免不确定性冲击愿意购买保险。虽然该理论模型可以较好解释VRP的存在及数量大小，但在解释期限结构方面仍存在一定的改进空间。

2.累积前景理论

行为金融理论从投资者自身行为特征出发，研究投资者何种行为模式可以解释方差风险溢价的存在。Baele等[9]从累积前景角度出发构建了VRP的理論框架，借助概率测度转换及损失厌恶两个设定，构建出满足数据特征的理论模型。具体而言，概率测度转换通过概率扭曲参数可以产生较高的二阶矩溢价，损失厌恶参数则保证此模型可以较好地解释一阶矩溢价。研究发现，累积前景理论可以较好地对价外股指期权定价。从上述模型设定中可看出，两个关键参数的设定是累积前景理论具有较强解释力的重要保证，但在实际中两个参数的引入和设定均缺乏坚实的理论基础。

3.无套利模型

另外一种理论基础模型从场外交易数据出发，借鉴套利定价模型（APT）的思想，推导出最适合数据特点的结构框架。DewBecker等[10]通过分析方差互换合约的实际成交数据，发现投资者对预期到的不确定性冲击较不敏感，而对未预期到、暂时性的已实现方差冲击较为敏感。场外交易数据反映出的曲线特征与许多理论模型都不吻合，如长期风险模型和累积前景理论等。受限于交易数据的时间长度，在数据量不断扩充后，该理论模型求解出的关键参数是否发生结构性突变仍然未知。endprint

（二）定价应用

学者们多从时间序列层面和横截面层面研究二阶矩的定价应用。时间序列层面，研究方差风险溢价对股权溢价、债券收益率等一阶矩指标的短期预测效果。Bollerslev等[3]研究了方差风险溢价对多期股权溢价的预测能力。研究表明，该预测能力在短期内达到最优，二阶矩溢价反映出消费增长的不确定性。Bollerslev等[5]进一步认为除消费增长的不确定性外，二阶矩溢价还反映出就业率增长的不确定性以及股票市场的流动性风险等因素。横截面层面，GonzlezUrteaga等[8]根据个股方差风险溢价的贝塔系数大小划分为20个等权重组合，其研究表明违约风险溢价（Default Premium）是决定横截面差异的主要因素。

三、 理论模型

Drechsler等[7]将跳跃项引入长期风险模型（简称为DY模型），将方差风险溢价分解为规模项差异和漂移项差异。其中，规模项差异测量了两种概率测度下方差的水平差异，漂移项差异测量了两种概率测度下方差的变动差异，本文的理论模型及参数设定均是在此基础上展开的。

（一）模型设定

（三）模型校调

本文选用的时间区间为1990年1月至2015年12月，共模拟1000次，参数设置见表1。表2为变量的统计特征，左侧为实际数据的统计参数值，右侧为模型拟合出5分位、50分位及95分位的统计参数值。

表3为经济模型和实际数据中方差风险溢价对多期超额收益率的预测结果，分别是未来一个月和三个月。从表中可看出，模型和实际数据中VRP的贝塔系数均保持良好的显著性（1%的显著性水平）。实际数据中调整后的R2要高于模型拟合的结果，表明该模型仍有进一步改进的空间。

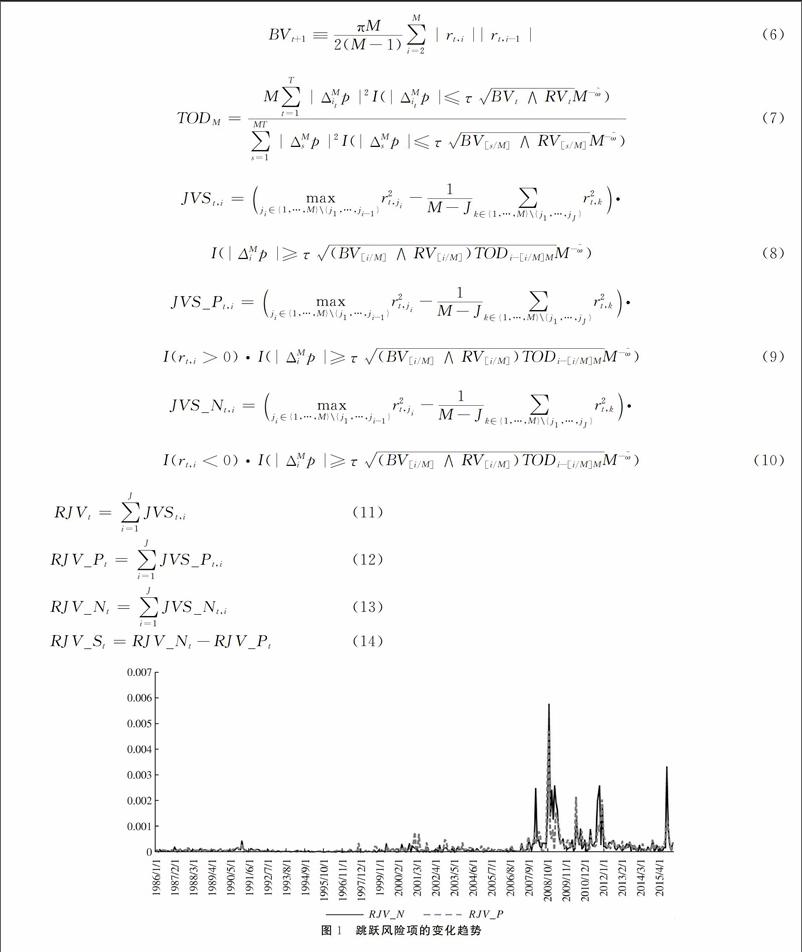
通过上述计算，可获得RV、BV、RJV、RJV_N、RJV_P和RJV_S在每个交易日的大小，以自然月为标准，将以上指标月内加总即为月度数值。负跳跃风险项和正跳跃风险项的变化趋势如图1所示。

图2为日内波动形态示意图，Bollerslev等[15]研究发现，日内波动形态呈“U”形。本文根据式（7）计算得出的TOD指标符合之前文献对该曲线的描述。

（三）数据说明

取样区间为1990年1月至2015年12月，交易时间为9：3016：00（美国东部时间）。每天共78个对数收益率，低于60个的样本删除掉，数据来源为交易和报价高频数据库（TAQ），隐含波动率指数（VIX）每天的交易数据取自沃顿商学院金融数据库（WRDS）。由于VIX是年化后的隐含波动率指数，故将其平方并除以12得到未来一个月的隐含方差。假定RV服从随机游走过程，由此可以计算出VRP在每个月的数值大小，即VRPt=IVt-RVt，如图3所示。

五、 实证分析

表4为对数超额收益率、隐含方差、已实现方差、各自的趋势项和波动项、控制变量、跳跃风险项、负跳跃风险项及正跳跃风险项的统计特征。其中，方差数值乘以了10000，收益率数值乘以了100。

根据上文VRP的计算结果，利用HP滤波方法分离出其中的波动项和趋势项。从图4可以看出，不确定性的趋势项与宏观经济形势联系较为紧密。首先，自1997年亚洲金融危机爆发以来，趋势项存在明显的下降走势，直至2007年金融危机爆发才逐渐上升。其次，自欧债危机后，全球量化宽松政策的实施导致流动性较为充足，趋势项又恢复下降的走势。最后，随着美联储加息预期的不断升温及美国新任总统带来不确定性的上升，趋势项的曲线拐点有望出现。在前文基础上，进一步利用HP滤波方法分离出隐含方差和已实现方差的波动项和趋势项，如图5所示。

本文的回归方程如式（15）—式（20）所示。其中，rext+j表示多期对数超额收益率（年化后），无风险利率使用3个月的国库券收益率来代替，h为月数。Xt为其他常见的控制变量，具体包括正负跳跃风险（RJV_P和RJV_N）、股利收益率（DP）、违约风险溢价（DEF）、期限风险溢价（TERM）及随机去趋势的无风险利率（RREL）等。RJV_P和RJV_N是根据BTL方法计算得出的跳跃风险项，除此之外，也引入了RJV和RJV_S作为控制变量。

首先，以调整后R2为比较标准。自变量分别为VRP、VRP波动项、IV和RV波动项时，各自对多期对数超额收益率进行回归（式（15）—式（17））。其中，预测区间为未来1个月至12个月，结果如图6所示。

从图6可以看出，三个方程（式（15）—式（17））的预测能力均在4个月时达到最高。其中，在以IV和RV波动项作为自变量的方程中，调整后的R2高达177%。通过比较分析，波动项在9个月及以下时，解释能力稍强，趋势项在9个月以上时，解释能力稍强。

（一）短期预测效果对比

接下来本文以4个月为比较基准，进一步比较引入控制变量后三个方程（式（18）—式（20））的显著性高低。由于在回归过程中存在区间重叠，故使用NeweyWest方法对标准差进行调整，结果见表5。VRP、VRP波动项、IV和RV波动项均保持良好的显著性，均在1%的显著性水平下保持顯著。而VRP趋势项和IV趋势项在10%的显著性水平下均不显著。由正负跳跃风险项的t值可知，负跳跃风险项在10%的显著性水平下显著，正跳跃风险项则不显著，两者对超额收益率的预测存在非对称性机制。

进一步验证该非对称性预测机制的稳健性，使用式（18）进行回归，结果见表6。RJV_N的预测能力明显强于RJV_P。加入控制变量后，RJV_P的t值迅速降低，而RJV_N依然保持显著（10%的显著性水平），且与未来多期超额收益率保持正相关关系。

（二）中长期预测效果对比

当h大于9个月时，波动项不再显著，而趋势项

的显著性有较大程度的提升。以VRP趋势项和波动项为回归对象，同样使用NeweyWest方法对标准差进行调整。预测结果见表7，波动项的贝塔系数在9个月以后不再显著（10%的显著性水平），而趋势项的贝塔系数在9个月之后保持显著（10%的显著性水平），其t值呈递增趋势。当预测区间较长时，跳跃风险项不再显著，表明该变量仅能影响短期内的超额收益率。endprint

（三）滾动窗口回归

以上分析了样本内回归的结果，出于稳健性考虑，本文接下来使用滚动窗口的方式，进一步验证波

动项和趋势项作用区间的不同。其中，滚动窗口使用120个月，预测区间为未来12个月，标准差使用NeweyWest方法调整。如图7所示，在193个样本回归中，波动项的t值在多数情况下小于196，而趋势项的t值在多数情况下大于196。

六、 结论

综上，本文将经济不确定性的代理变量VRP拆分为趋势项和波动项，并比较了其作用机制的差别。其中，短期内波动项对未来多期超额收益率具有显著的预测作用，中长期内趋势项则对未来多期超额收益率具有显著的预测作用。由于两项加总仍为VRP，表明短期内VRP的预测能力更多来自于波动项，中长期内其预测能力更多来自于趋势项。通过将隐含方差和已实现方差进一步拆分，发现整体的预测效果存在明显提升。对VRP趋势项的研究发现，欧债危机后美国经济不确定性一直在下降，但随着投资者对美联储加息预期的不断升温，其周期性拐点有望在近期出现。

此外，本文基于5分钟高频数据研究了股票市场上跳跃风险项对股权溢价的预测能力。采用Bollerslev等[15]的研究思路构建了跳跃风险指标，并重点分析了正负跳跃风险项与股权溢价的相关关系。研究发现，正负跳跃风险项的预测能力存在显著的非对称性。其中，负跳跃风险项的预测能力较强，而正跳跃风险项的预测能力较弱。参考文献：

[1]Manela A， Moreira A. News implied volatility and disaster concerns [R]. Washington University Working Paper， 2015.

[2]Baker S R， Bloom N， Davis S J. Measuring economic policy uncertainty [R]. Northwestern University Working Paper， 2016.

[3]Bollerslev T， Tauchen G， Zhou H. Expected stock returns and variance risk premia [J]. Review of Financial Studies， 2009， 22（11）： 44634492.

[4]Bekaert G， Hoerova M， Marco L D. Risk， uncertainty and monetary policy [J]. Journal of Monetary Economics， 2013， 60（7）： 771788.

[5]Bollerslev T， Gibson M， Zhou H. Dynamic estimation of volatility risk premia and investor risk aversion from optionimplied and realized volatilities [J]. Journal of Econometrics， 2011， 160（1）： 235245.

[6]Bekaert G， Hoerova M. The vix， the variance premium and stock market volatility [J]. Journal of Econometrics， 2014， 183（2）： 181192.

[7]Drechsler I， Yaron A. Whats vol got to do with it [J]. Review of Financial Studies， 2010， 24（1）： 145.

[8]GonzlezUrteaga A， Rubio G. The crosssectional variation of volatility risk premia [J]. Journal of Financial Economics， 2016， 119（2）： 353370.

[9]Baele L， Driessen J， Londono J M， et al. Cumulative prospect theory and the variance premium [R]. Tilburg University Working Paper， 2014.

[10]DewBecker I， Giglio S， Anh L， et al. The price of variance risk [R]. Northwestern University Working Paper， 2014.

[11]Bansal R， Yaron A. Risks for the long run： A potential resolution of asset pricing puzzles [J]. Journal of Finance， 2004， 59（4）： 14811509.

[12]Campbell J Y， Shiller R J. The dividendprice ratio and expectations of future dividends and discount factors [J]. Review of Financial Studies， 1988（1）： 195228.

[13]Campbell J Y， Shiller R J. Stock prices， earnings， and expected dividends [J]. Journal of Finance， 1988b， 43： 661676.endprint

[14]Guo H， Wang K， Zhou H. Good jumps， bad jumps， and conditional equity premium [R]. University of Cincinnati Working Paper， 2016.

[15]Bollerslev T， Todorov V， Li S. Jump tails， extreme dependencies， and the distribution of stock returns [J]. Journal of Econometrics， 2013， 172： 307324.

[16]BarndorffNielsen O E， Shephard N. Power and bipower variation with stochastic volatility and jumps [J]. Journal of Financial Econometrics， 2004（2）： 137.

[17]Andersen T G， Bollerslev T， Diebold F X. Roughing it up： Including jump components in the measurement， modeling and forecasting of return volatility [J]. Review of Economics and Statistics， 2007， 89： 701720.

[18]Lee S S， Mykland P A. Jumps in financial markets： A new nonparametric test and jump dynamics [J]. Review of Financial Studies， 2008， 21： 25352563.

[19]Sheppard K， Patton A J. Does anything beat 5minute rv？ A comparison of realized measures across multiple asset classes [R]. University of Oxford Working Paper， 2013.

责任编辑、 校對： 高原endprint