变刚度弹簧式恒流阀的结构设计与分析
黎少辉,李建松
变刚度弹簧式恒流阀的结构设计与分析
黎少辉,李建松
(徐州工业职业技术学院,江苏 徐州 221140)
针对现有机械自力式恒流量控制阀结构多目标优化设计难点,提出基于圆锥环状缝隙为控制流道的变刚度弹簧式恒流阀的设计方案,并采用-标准湍流模型,对不同压差下的出口流量进数值字模拟,结果显示,在压力波动范围(30~150 kPa)内该恒流阀平均流量理论误差可控制在0.19%左右,精度高,结构简单,通流能力大。
圆锥环状缝隙;变刚度弹簧;恒流阀
近年来,为减小压力波动对流量的影响,相关恒流量阀的研究成为控制阀阀领域研究热点。Young-Ho Cho设计了一种基于恒刚度弹簧薄片的无泵恒流量控制阀,用于汽车发动机的供油系统。由于该系统提供汽油的微流量控制,尽管流量与微缝隙大小成非线性关系,其恒流量控制精度仍可达6%左右[1];汤中彩、王琦等[2-3]设计一款通流能力大的恒流量控制阀,阀芯轮廓优化采用同心缝隙流量公式与阀芯受力平衡方程组合反求获得的,但阀芯挡环的轮廓采用尝试法进行优化设计,设计工作量大,精度不易保障,进而造成阀芯外轮廓移动中与挡环轮廓的配合难以满足要求。基于此,设计一种变刚度弹簧式圆锥环状缝隙恒流量阀,该恒流阀的阀芯截面轮廓在移动始终与挡环的截面轮廓形成平行的缝隙,保证阀芯移动中的通流截面的一致性,只要实现支撑阀芯的变刚度弹簧的优化设计唯一目标即可满足该恒流阀的精确控制。目前,变刚度弹簧在汽车及其它减震器中得到成熟而又广泛应用[4-5],随着先进制造技术的发展,如3D打印技术等,复杂变刚度弹簧制造变得易于实现。
1 变刚度弹簧式恒流阀的结构设计
汤中彩、王琦等[2-3]设计的线性弹簧式恒流量控制阀结构如图1所示。该阀的阀芯轮廓采用了同心圆环缝隙流量公式(1)与负载平衡公式(2)的组合公式(3)反求获得的,阀芯轮廓精度得到保障。但与阀芯配合的挡环轮廓采用尝试法进行优化设计,工作量大,精度难以保障。

式中:为通过同心环缝隙流量,m3/s;Δ为同心圆柱环状间隙进出口压差,Pa;为流体的动力粘度,Pa·s;为环形缝隙深度,mm;为同心圆环外圆环半径,mm;为同心圆环内圆环半径,mm。


式中:r1为阀芯最右端截面半径。
基于此,设计一种变刚度弹簧式恒流量控制阀,如图2所示。该控制阀阀芯与挡环形成圆锥环状通流间隙,阀芯支撑采用变刚度弹簧,其它结构与图1所示的结构相似。

图2 变刚度弹簧式恒流阀结构示意图
2 变刚度弹簧式恒流阀控制原理
2.1 圆锥环状缝隙流量公式
圆锥环状缝隙结构如图3所示。1994年尤明庆等[5]通过坐标变换,得到用于研究圆锥环状区城流动的N-S方程。对内外锥面相对旋转和缝隙泄漏这两种状态进行了求解。结果表明,就速度分布而言,厚度占的圆锥环状缝隙相当于厚度为cos的圆柱环状缝陈,为半锥角。进而得出圆锥环状缝隙流量公式(4)。

图3 圆锥环状缝隙结构示意图

2.2 变刚度弹簧理论基础
祁宏钟、陈德强等[7-8]在变刚度螺旋弹簧的设计方法和精确建模做了深入的探讨,实现变刚度特性的变弹簧中径、变簧丝直径和变螺旋角螺旋弹簧的设计方法,为变刚度式恒流阀的设计奠定理论基础。
对于普通小螺旋升角的压缩螺旋弹簧的变形计算公式如下[9]:
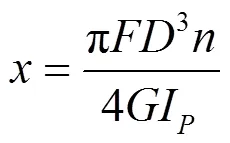
式中:为弹簧载荷,N;为弹簧中径,mm;为有效圈数;为弹簧材料的切变模量,GPa;I为为弹簧材料截面极惯性矩,mm4。
对于一般圆形截面材料,极惯性矩I=π4/32代入式(5),得:
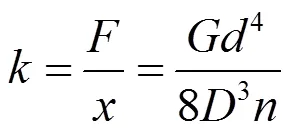
式中:为簧丝横截面直径,mm。

根据式(4)可知,当流量确定后,即可画出Δ-之间的曲线图。设定精度要求,采用粒子群、遗传算法等成熟的优化算法获得Δ-曲线的拟合折线,通过拟合折线与Δ-的交点获得多个坐标点(Δ,)的大小。如图4所示,确定流量=6.8 kg/s,Δ波动范围有的大小确定,取值范围(3~6.5 mm)。采用粒子群优化算法,设置8个点,群体取400,迭代600次,最终优化流量结果误差和为0.0351(351个点),均点误差0.01%。
把获得的坐标点(Δ,)值代入弹簧负载平衡公式(7),即可得到多个刚度系数。

式中:为阀芯的最大截面积,m2;0为为初始缝隙宽度,mm。
然后再将获得刚度系数分别代入式(6)即可求得弹簧丝的多段直径大小,再根据弹簧材料选择及满足强度要求,可确定弹簧的其它参数[9],为变刚度弹簧造型奠定基础。具体造型可参考祁宏钟、陈德强等[7,8]所介绍的方法进行建模,即可获得满足圆锥环状间隙恒流阀所需的变刚度弹簧模型。

图4 Δp-δ曲线及拟合折线
3 仿真分析
以图2结构设计一种流量为6.8 kg恒流量控制阀,出口压力2=50 MPa,为恒定压力;进口压力1与出口压力2压差波动范围(Δ=20~200 kPa),通过式(4)确定=20 mm,=30 mm,=30°。采用ANSYS Fluent 14.0软件进行流场仿真,Δ在波动范围内随机选取30 kPa、40 kPa、50 kPa、60 kPa、70 kPa、100 kPa、150 kPa、200 kPa,计算选择标准-湍流模型,自适应网格划分,设置监控出口流量。部分仿真流场及出口流量迭代收敛曲线如图5、图6所示,监控出口流量如表1所示。
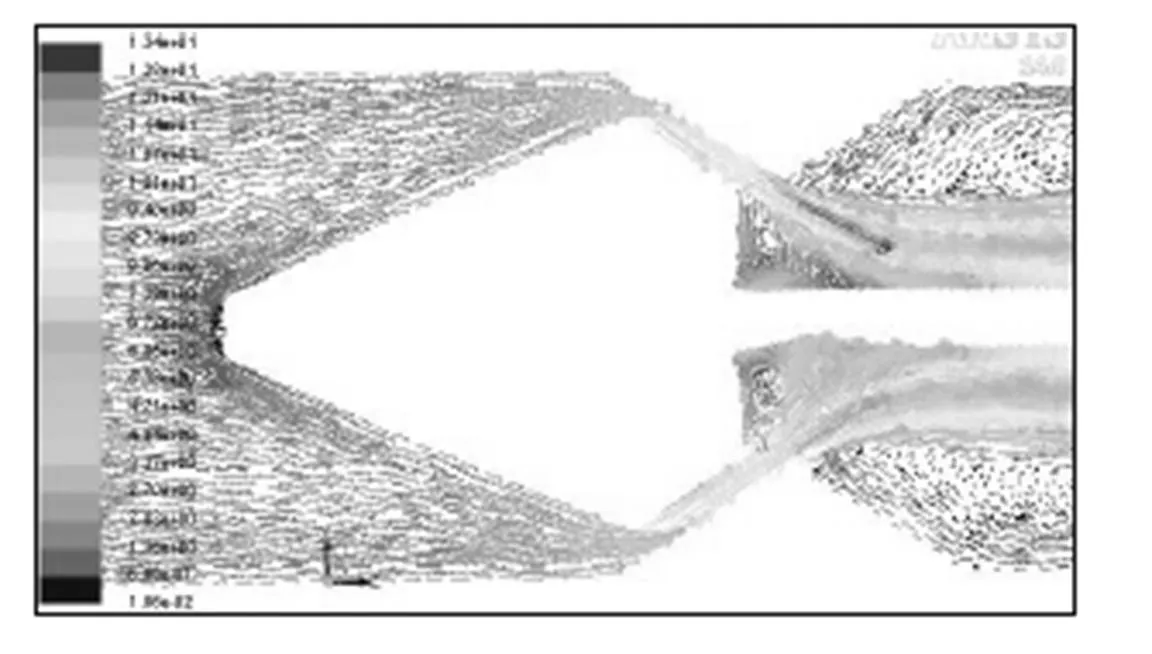
图5 Δp=50 kPa时恒流阀内部流场图

图6 恒流阀出口流量监控迭代曲线

表1 多个压差下的仿真流量及误差
从表1可以看出,当Δ≤30 kPa时,流量负误差高于8%,这是由于压差较小,流体动能、压力能较小,相应的能量损耗比较大,造成流量负误差较大;随着进出口压差增大,流体动能、压力能增大,恒流阀流道结构不变,相应能量损耗比降低,流量误差逐渐减小,并从负误差逐渐转向正误差;当Δ≥150 kPa时,流体动能、压力能进一步增大,能量损耗比进一步降低,流量正误差逐渐增大到6%以上。但是从压差波动范围(30~150 kPa)平均流量来看,流量平均误差可控制在0.19%左右,具有很高的恒流量控制精度。
4 结论
(1)利用圆锥环状间隙作为恒流量控制阀的控制流道,简化结构设计,易于保证阀芯移动中的通流截面形状的一致性。
(2)利用变刚度弹簧自适应控制压力波动造成圆锥环状间隙宽度变化,容易实现流量的精确控制。
综上所述,基于流体通过圆锥环状缝隙流道时流量与缝隙宽度的非线性关系,针对性的利用变刚度弹簧自适应压力波动与圆锥环状间隙宽度变化,实现流量精确恒定控制是可行的,且结构简单,通流能力大。
[1]Young-Ho Cho. Pumpless Fuel Supply Using Pressurized Fuel Regulated by Autonomous Flow-Rate Regulation Valves[J]. Journal of Fuel Cell Science and Technology,2012,9(6):034503-1-034503-4.
[2]汤中彩,麻剑锋,沈新荣. 一种新型恒流量控制阀的研究[J]. 工业仪表与自动化装置,2012(1):11-12.
[3]王琦,张江兵,饶军. 恒流量控制阀的数值模拟和优化设计[J]. 液压与气动,2013(12):38-41.
[4]王红,汤劲松,刘万选. 车辆变刚度弹簧组模糊可靠性分析方法研究[J]. 铁道学报,2015(8):24-28.
[5]YU Haitao,LI Mantian,CAI Hegao. Analysis on the Performance of the SLIP Runner with Nonlinear Spring Leg[J]. CHINESE JOURNAL OF MECHANICAL ENGINEERING,2013,26(5):892-898.
[6]尤明庆,于乃颖,韩中原. 圆锥环状缝隙内的流动状态[J]. 焦作矿业学院学报,1994(12):66-70.
[7]祁宏钟,雷雨成,冯晋祥. 变刚度螺旋弹簧的设计方法和精确建模初探[J]. 中国机械工程,2002(7):1100-1103.
[8]陈德强,王红,商跃进. 铁路货车变刚度弹簧组计算机辅助设计系统研发[J]. 兰州交通大学学报,2009(12):91-94.
[9]刘向峰. 机械设计课程[M]. 北京:清华大学出版社,2008.
The Structure Design and Analysis of Variable Stiffness Spring Type Constant Flow Control Valve
LI Shaohui,LI Jiansong
(Xuzhou College of Industrial Technology, Xuzhou221140, China)
Aiming at reducing the difficulty of multi-objective optimization in the design of constant flow control valve, a variable stiffness spring constant flow control valve(VSSCFCV) was designed to be used in conical gap flow.-turbulence model was used to calculate the outlet flow in different pressure differential. The average flow rate error can be controlled at around 0.19% when pressure fluctuation ranges from 30 to 150 kPa. The simulated results show that VSSCFCV has high flow controlling precision, simple structure and good flow capacity.
conical gap;variable stiffness spring;constant flow control valve
TH138.52+2
A
10.3969/j.issn.1006-0316.2018.01.010
1006-0316 (2018) 01-0046-04
2017-05-03
江苏省“青蓝工程”资助项目(QLGC-2013-04);江苏省高职院校高级访问学者计划项目(2015FX085)
黎少辉(1974-),男,河南郑州人,博士,副教授,主要研究方向为流体机械优化设计研究、机械CAD/CAM/CAE应用技术。

