基于有限元的低风压导线结构分析

周 超，陈 作，李 力，刘衍平，宋玉旺



基于有限元的低风压导线结构分析

周 超1，陈 作1，李 力2，刘衍平1，宋玉旺1

(1. 华北电力大学能源动力与机械工程学院，北京 102206；2. 北京送变电公司，北京 102401)

为降低导线表面风压，近年来国内外学者提出了多种截面形状的低风压导线,验证了其工作机理。然而，鲜见涉及低风压导线结构稳定性、放线跳股问题的研究。为此，利用ANSYS软件对架空线路中常用的钢芯铝绞线和低风压导线建立有限元模型，并结合导线放线时发生跳股的判定依据，分析不同工况下，导线放线时的位移云图与结构稳定性，探讨最外层导线根数与导线结构稳定性的关系。结果表明，低风压导线最外圈导线根数越多，导线结构越稳定。

低风压导线；放线；有限元分析；稳定性

风载荷是架空线路设计中需要考虑的一个关键因素。风压会增加导线的张力，引起导线摆动，在很大程度上影响了铁塔本体和基础的强度设计。在实际运用中，导线承受了整个线路体系中50%~70%的风压，因此如何降低导线所受到的风压，确保线路体系的安全运行是近年来导线研究的重点。与目前架空线路中广泛使用的钢芯铝绞线相比，低风压导线的阻力系数较小，受到的风压更小，提高了线路运行的安全性，降低了铁塔的强度设计要求[1]。低风压导线在放线滑车时，由于较大的综合外力的作用，结构容易处于失稳状态，出现跳股现象。这不仅严重影响了架空线路施工的进度和质量，还给线路的安全运行增加了隐患。因此，研究低风压导线的稳定性具有较大的现实意义。

目前，国内外学者已经对低风压导线开展了广泛的研究。20世纪80年代，SAKAKIBARA等[2]详细阐释了低风压导线的特性和发展。20世纪90年代，木村容康和青木克己[3]进一步研究了低风压导线的机理和应用。我国对低风压导线的研究起步较晚，但发展前景广阔。胡渊蔚[1]阐述了低风压导线的机理，并介绍了低风压导线的测试和发展过程。尤传永[4]对输电线路低风压导线的开发研究进行了详细地说明。国内外对低风压导线的研究多建立在对其机理和发展的探讨上，未对放线滑车时低风压导线的稳定性进行系统地评估，因此导线的合理运用仍存在不足。

本文对放线滑车时低风压导线的结构稳定性进行了仿真分析，利用跳股判据评价其稳定性。利用ANSYS软件建立了普通钢芯铝绞线a和5种低风压导线b，c，d，e和f的有限元模型以及滑车模型，6种导线的编号及名称见表1。对导线在25%张力条件下，以30°包络角通过20倍导线直径的放线滑车时的结构稳定性进行了仿真分析，探讨最外层导线根数与导线结构稳定性的关系。

表1 导线编号及名称

1 低风压导线的特性

对低风压导线的研究多着重于对其风阻力系数的探讨上，风阻力系数影响着低风压导线性能的好坏。尤传永[4]认为要减小处于流体中的圆柱体或标准导线的阻力，必须减小其阻力系数，即设法使其处在超临界状态，且表面具有一定“粗糙度”的球体或圆柱体的风阻力系数更小。胡渊蔚[1]发现，阻力系数主要取决于雷诺数，此外还与物体表面的粗糙度、来流的紊动强度以及物体的形状有关。因此，通过对导线形状或粗糙度的合理优化，可以得到性能优越的低风压导线。

和架空线路中常用的传统钢芯铝绞线相比，低风压导线的外层线股使用扇形截面，可以使导线圆周更加平滑，外径较小；同时相邻扇形截面的圆弧形成V槽，使导线表面具有一定的粗糙度，有利于减小导线的阻力系数，降低风压。图1分别为普通钢芯铝绞线和低风压导线的结构简图。

图1 导线结构简图

2 导线跳股现象

对绞线结构进行稳定性分析时，需要建立单根导线的有限元模型及其接触关系，模型非线性大，预测结果受摩擦、预应力等影响，稳定性预测难度大。本文采用有限元软件ANSYS建立6种钢芯铝绞线模型，分析存在25%张力和与滑车保持30°包络角时各单股间的相对变形，利用跳股判据评价其稳定性。

2.1 股线受力分析

对导线的某一微段进行受力分析，如图2所示。导线受到沿着轴线方向的拉力，轴向力平移到各股线截面中心与螺旋股线引起的弯矩和中心股线间的摩擦对螺旋股线产生的弯矩叠加的总弯矩。

图2 导线微元段受力图

股线沿自身轴线切线方向拉力为

导线所承受的拉力为

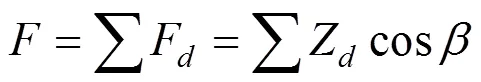
中心股线截面上的应力为

螺旋股线截面上的应力为

其中：F为股线沿轴线方向的分力；为股线螺旋角；为股线截面面积；为惯性矩；为距离中性轴高度。

中心股线轴线与导线轴线重合，受到的外力与轴线共线，因此钢芯铝绞线中心股线只承受拉伸载荷，截面上只存在拉伸应力；螺旋股线承受拉伸载荷和弯曲载荷，截面上存在拉伸应力和弯曲应力。

2.2 股线跳股判据

绞线的跳股判据为：当最外层任一铝线突出于相邻铝线，则表明其处于跳股状态，如图3所示。

图3 跳股判据示意图

计算绞线的跳股系数为

其中；R为加载变形后最外层第根导线中心到最内层钢丝变形后的中心距离；R+1为加载变形后最外层第+1根导线中心到最内层钢丝变形后的中心距离；ex为导线最外层铝线的等效半径；当小于时未发生跳股，∈[0.5,1.0]为跳股参考值[5]。

绞线通过滑车时，存在3种载荷：“25%张力”、“30°包络角”和“导线滑动”。其中，“25%张力”可以采用预应力方式模拟；“30°包络角”可以采用先建立直导线，后逐渐移动滑车使导线弯曲来模拟；通过固定导线一端，可以使得逐渐移动滑车过程中导线相对于滑车滑动，以模拟“导线滑动”引起的横截面变形的累积效应。

本文的分析方案见表2。

表2 分析方案

3 有限元模型

3.1 普通钢芯铝绞线有限元模型

普通钢芯铝绞线a由7根钢线与45根铝线分5层绞合而成，外径为33.75 mm。由于缺乏确定的节径比数据，本文根据工程经验选取节径比。每层导线的参数见表3。

表3 普通钢芯铝绞线每层导线的参数

表3中，铝合金弹性模量为70 GPa，泊松比为0.3；钢的弹性模量为200 GPa，泊松比为0.3。本文采用实体单元对导线建立有限元模型，基于对股线受到外载荷作用发生弹塑性变形和股线间的相互接触等问题的考虑，选用8节点的Solid185单元[6]。导线内的接触分为3种[5]：中心股线与螺旋钢股线间的线接触、相临绞线层股与股间的点接触、同绞线层内股线间线接触。首先建立各绞线层的截面，划分接触体和非接触体；其次利用平移、旋转命令生成局部接触体；然后复制生成接触体；重复以上步骤，最后建立非接触体，生成完整的导线几何模型，如图4所示。

建模时，初始状态为导线伸直，导线总长度为50倍直径。单根导线均采用梁单元模拟，相邻两根导线之间定义接触。滑车采用单R槽类型，槽底半径R=36 mm，滑轮槽倾斜角=15°。模型中采用30°中心角的圆形轨道模拟，滑车与导线在导线中点处接触，两者之间没有接触压力。结构有限元模型如图4所示。

理论分析表明，单根导线之间摩擦系数越小导线稳定性越差，一般钢-钢、钢-铝、铝-铝的摩擦系数大于0.1，分析时在单根导线之间采用0.1作为摩擦系数；滑车和导线之间摩擦系数越高导线稳定性越差，实际工作中导线和滑车是滚动摩擦，滚动摩擦系数很小，远小于0.1，本文采用0.1作为摩擦系数。采用上述方法，可以得到工程保守结果。

模拟过程分成两步：

步骤1. 导线两端固定垂直于导线轴线的位移。固定滑车位置。导线一端固定沿导线轴线位移，另一端施加37.6 kN拉力(37.6=150.45×25%)。载荷及约束条件如图5(a)和(b)所示。

步骤2. 滑车在滑车圆形轨道平面内沿垂直导线方向挤压导线。当绞线与滑车的包络角达到30°时完成计算。载荷及约束条件如图5(c)所示。在滑车挤压绞线过程中根据图6的几何分析可见，导线会相对滑车滑动，滑动距离约为27.6 mm，这可以模拟导线滑动时横截面变形的累积效应。

图5 模拟步的约束条件及加载情况

图6 模拟过程中绞线相对于滑车滑动情况分析

图6中，以绞线轴线的长度作为计算长度，各参数的单位为(mm)，则

=33.75×21/2×sin15°=91.7 (mm)

=33.75×50/2=843.8 (mm)

=-=752.0 (mm)

=/ cos15°=778.6 (mm)

(弧长)=33.75×21/2×15/180π=92.8 (mm)

=×sin15°+(-× cos15°)=202.1 (mm)

=+-=27.6 (mm)

其中，为滑车运动距离；为导线相对滑车滑动距离。

3.2 低风压钢芯铝绞线有限元模型

5种低风压导线的截面形状如图5所示。5种低风压钢芯铝绞线的有限元模型建模方法同上，最外层节径比均选为9。5种低风压钢芯铝绞线有限元模型的横截面图如图7所示。

4 结果分析

利用有限元模型，分两步进行绞线稳定性分析。在建好的导线模型上利用自由网格划分生成单元，按照步骤1和步骤2中的要求对模型施加载和添加约束，通过分析计算后得到位移云图。图8~13分别为钢芯铝绞线a及5种低风压导线：b，c，d，e和f模拟步骤1结束时绞线的位移云图，模拟步骤2结束时模型的位移云图及绞线与滑车接触部位的局部位移云图。

从图中可以看出，模拟步骤1中钢芯铝绞线a沿轴的最大位移最小，其他低风压导线沿轴的最大位移相近；模拟步骤2中钢芯铝绞线f沿轴的最大位移最小，钢芯铝绞线a沿轴的最大位移最大。

采用式(5)计算最外层所有单根导线的跳股系数λ，取其最大值作为本工况的跳股系数。通过计算发现钢芯铝绞线a、b、c、d、e、f的跳股系数分别为0.088、0.364、0.246、0.498、0.359、0.349，均小于的参考区间，所以均不会发生跳股。

图8 钢芯铝绞线a位移结果

图9 钢芯铝绞线b位移结果

图10 钢芯铝绞线c位移结果

图11 钢芯铝绞线d位移结果

图12 钢芯铝绞线e位移结果

图13 钢芯铝绞线f位移结果

5 结 论

采用ANSYS软件对一种普通钢芯铝绞线和5种低风压钢芯铝绞线共6种钢芯铝绞线，在30°包络角，25%张力条件下通过20倍导线直径的放线滑车时绞线各单股导线的变形进行分析，采用跳股判据对绞线的结构稳定性进行评价，得到6种方案的跳股系数分析结果见表4。

表4 6种方案的跳股系数分析结果

分析结果表明：

(1) 普通钢芯铝绞线a的跳股系数为0.088，远小于工程中[0.5,1]的要求，导线结构稳定。

(2) 5种低风压钢芯铝绞线b、c、d、e和f的跳股系数最大值为0.498，最小值为0.246，均小于工程中[0.5,1]的要求，导线结构稳定。

(3) 5种低风压钢芯铝绞线中d的跳股系数最大，c的跳股系数最小。d最外圈导线根数为12，c最外圈导线根数为18，另外3种绞线最外圈导线根数均为16。通过比较，发现低风压导线中，最外圈导线根数越多，跳股系数越小。

[1] 胡渊蔚. 低风压导线的发展和测试[J]. 电线电缆, 2016(5): 1-5.

[2] SAKAKIBARA A, LISAKA H, MORI N, et al. Development of low-wind-pressure conductors for compact overhead transmission line [J]. IEEE Power Engineering Review, 1984, 103( 10): 3117-3124．

[3] 木村容康, 青木克己. 低風圧電線の特性と流れ様式[J]. 可視化情報学会誌, 1997, 17(2): 315-318．

[4] 尤传永. 输电线路低风压导线的开发研究[J]. 电力建设, 2010, 31(12): 1-6.

[5] 万建成, 司佳钧, 刘彬, 等. 一种结构稳定的大截面扩径导线设计[J]. 电力建设, 2013, 34(10): 92-96.

[6] 万建成, 董玉明, 杨文刚, 等. 扩径导线的参数化有限元建模[J]. 电力科学与工程, 2015, 7(31): 74-78.

Analysis of Low-Wind-Pressure Conductor Based on Finite Element

ZHOU Chao1, CHEN Zuo1, LI Li2, LIU Yanping1, SONG Yuwang1

(1. School of Energy, Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China; 2. Beijing Power Transmission and Distribution Company, Beijing 102401, China)

In order to reduce the wind pressure on the surface of the conductor, scholars at home and abroad have put forward a series of low-wind-pressure conductors with different section shapes and validated their working mechanism. However, there are few reports about the structural stability of the low-wind-pressure conductor and the problem of strand jumping. Therefore, the finite element model is established for aluminum conductor steel reinforced commonly used and low-wind-pressure conductor by ANSYS software. Based on criterion of strand jumping occurred on line, the displacement cloud and structural stability of the wire under different working conditions are analyzed. At the same time, the relationship between the number of outermost wire strands and the stability of conductor structure is discussed. The results show that the more the conductor number of the outer ring, the more stable the wire structure.

low-wind-pressure conductor; pay-off; finite element analysis; stability

TM 244+.2

10.11996/JG.j.2095-302X.2018010129

A

2095-302X(2018)01-0129-07

2017-04-12；

2017-07-16

国家自然科学基金面上项目(51575180)；北京自然科学基金面上项目(8152027)

周 超(1980-)，男，北京人，副教授，博士研究生。主要研究方向为机械动力学、非线性振动和结构设计。E-mail：zhouchao@ncepu.edu.cn