IIR数字滤波器设计与FPGA实现

陈鑫磊，辛晓宁，黄 鑫

（沈阳工业大学信息科学与工程学院，沈阳110870）

1 引 言

数字滤波器具有可靠性高、一致性好等优点，在许多应用领域使用数字滤波器替代模拟滤波器可获得更好的性能。与FIR滤波器相比，IIR滤波器具有更好的幅频特性。由于具有反馈回路，同FIR相比，IIR在相同阶数时取得的滤波效果更好。目前对于数字滤波器的设计多局限于软件仿真，在硬件实现时还需解决字长确定及浮点乘法定点化的问题。由于DSP硬件资源丰富运算能力强，使用DSP芯片实现数字滤波器软件设计较为简单，但硬件系统较为复杂。与DSP相比，FPGA在成本、功耗、灵活性上都更有优势[1]。针对二进制数的特点对乘法运算进行了优化。在不使用硬件乘法器及IP核的前提下，使用较少的逻辑单元实现了滤波器功能，并进行了实际测试。实验结果与理论设计吻合，达到了预期的滤波效果。

2 滤波器的设计

2.1 滤波器的结构

根据实际需要选择滤波器阶数为六阶，由于使用六阶直接型结构将会带来较大的误差积累[2]。因此选择使用三个二阶滤波器级联的结构来实现，每个二阶滤波器传递函数如下式所示：

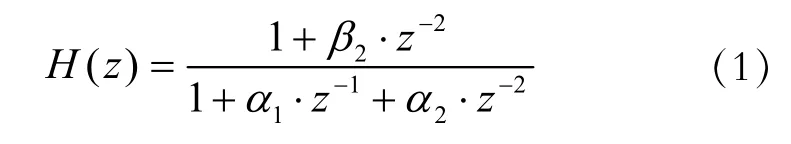
滤波器类型选择巴特沃斯滤波器，因其幅频特性单调下降，相频特性也是单调下降，对信号产生的幅值畸变和相位畸变都很小[3]。

2.2 滤波器参数的确定

滤波器主要参数包括：采样率28.8kHz、下限截止频率1kHz、上限截止频率3kHz。阶数为六阶，结构采用由二阶直接型级联[4]构成，阻带衰减倍数由软件优化至最佳。由于软件设计的滤波器增益是归一化的，在每个二阶结构中都会除以一个系数，保证通带信号增益为0dB。考虑到实际使用中输出数据字长大于输入数据字长，所以滤波器在通带可以有一定增益。将每节的除法省略在降低计算复杂度的同时，可以增加计算字长减少量化误差。最终得出的幅频特性、相频特性曲线如图1所示，根据系统的零极点分布可得出滤波器是稳定的。

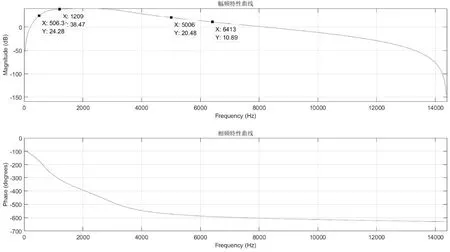
图1 幅频及相频特性曲线

2.3 滤波器字长的确定

滤波器设计完成后将参数导出，得到传递函数如下式所示：

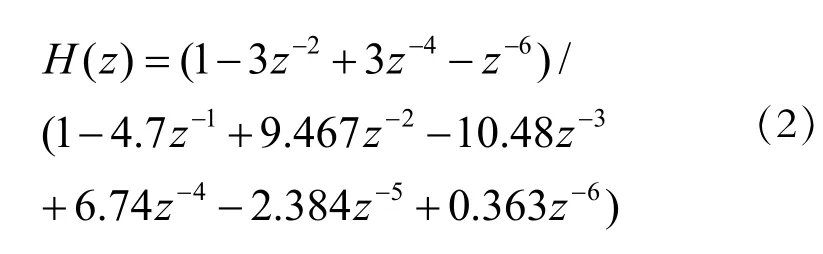
为保证滤波器在计算的过程中数据不发生溢出，需要了解实际使用过程中各节点可能出现的最值来确定字长。通过在Simulink环境下建立滤波器仿真模型[5]，将6位二进制数表示的正弦波按照采样率送入滤波器，可观察到各节点数据的变化范围。存储计算结果的寄存器的字长按照实际需求设定，为了保证计算精度防止溢出，计算单元的字长需要留有余量。根据模型仿真的结果可以确定寄存器使用12位字长，计算使用14位字长。

3 滤波器系数量化

3.1 系数量化方法

滤波器结构如图2所示，一共有6个浮点系数，实际实现时需要定点化。定点化可以通过将系数扩大一定倍数后取整，计算乘法后再除以扩大倍数来实现。该方法需要进行除法计算，电路复杂。为了减小定点化带来的误差，需要将系数扩大较大的倍数，这就增加了运算的字长。运算电路字长的增加，一方面增加了电路复杂度，另一方面也降低了运算速度。

为了在保证计算精度的前提下尽可能的减小字长，可以将乘法转化为多个除法结果的加减法来进行，交换乘除法的顺序可以更有效的利用字长保证数据不会溢出。二进制数的除法可以用移位代替，根据所乘系数的不同借助CSD编码可以找到在可承受的精度误差内最接近的逼近结果，使用最简单的电路实现理想的计算精度。由于计算过程中数据均为有符号数，减法实际使用加补码实现，所以电路只需要实现移位以及加法即可。

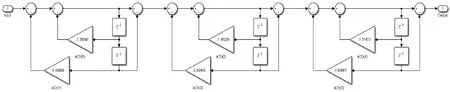
图2 滤波器结构图

3.2 系数编码及验证

CSD编码[6-7](Canonic Signed Digit)即正则有符号数字系统，可将系统化简为最少非零元素实现，从电路结构上看，最少非零元素即为运算单元级数最少。CSD编码有三重值，除0、1外还引入了-1帮助化简，为表示方便这里用2表示。从最低有效位开始用10…0(-1)代替所有1连续个数大于2的序列，使用110(-1)代替1011序列，从最高有效位开始用10(-1)代替011，可得到对应的CSD编码。以十进制数123为例说明CSD编码过程，123转化为二进制表示

由高位开始替换011序列的结果

从低位开始替换连续的1序列得到最终结果

通过比较编码前后的结果原序列有六个非零项，而编码后只有三个非零项简化了运算，为检验编码的正确性可以将CSD编码还原为十进制数与编码前一致。

以系数1.86229为例说明乘法计算的优化方法，首先根据数据位宽及需要的精度确定移位的最大值n，n值的选取参考模型仿真的结果决定这里选8。将系数乘以2n后取整

将结果转化为二进制表示

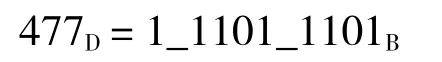
借助CSD编码进行简化

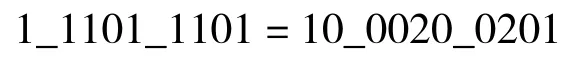
对应位为1代表加2代表减，从左至右各位的权重为20到2-7逼近结果如下

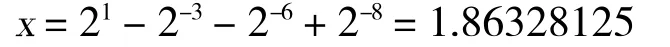
计算逼近误差

Δ=1.86328125-1.86229=0.00099125

经过优化，任意数乘1.86229的结果可以用该数左移1位加右移8位减右移3位、6位进行逼近，实现的增益为1.86328125，而对应的电路除移位外只需要三级加法器即可。所有系数的优化结果如表1所示。

表1 滤波器系数逼近结果

4 滤波器的描述及Modelsim仿真

使用Verilog语言按照滤波器结构对电路进行描述，寄存器的位宽由模型仿真给出，浮点乘法由移位以及加法替代，在描述过程中注意时序，防止将未算完的结果存入寄存器。

在计算过程中所有数据为有符号数，对数据进行计算及移位时要考虑到对符号位的影响。输入信号由Matlab产生，将幅度为10频率为1.2kHz的信号与幅度为5频率分别为500Hz、5kHz、6kHz的噪声混合作为输入，导入Modelsim编写测试文件，按照时序将数据逐个送入滤波器，同时将滤波器的输出数据记录到文件。使用Matlab对滤波器的输入输出结果进行FFT计算，输入输出波形及分析结果如图3所示。

根据设计采样率为28.8kHz，对系统进行1024点FFT运算，采用如下公式：

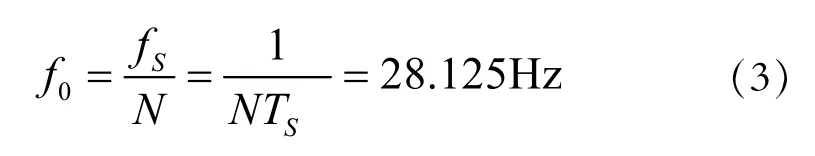
由公式 (3)计算得出对频率的分辨率为28.125Hz，可有效区分施加的四种信号。输入信号频谱图可以看到4个明显的尖峰，经过滤波器处理后输出信号的频谱图只在通带内存在一个尖峰，通带外的噪声被有效滤除，滤波效果明显。

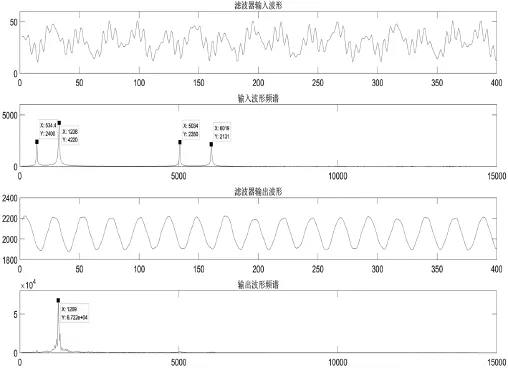
图3 滤波器输入输出结果分析

5 实验测试

为进一步验证滤波器的实际性能，使用FPGA、模数转换器、数模转换器搭建实验平台进行实际测试。模数转换器使用AD9280，输出为8位并行数字量[8]，实际使用高六位；数模转换器使用TLC5615，通过串行接口控制，将12位数字量转化为模拟电压[9]。输入由信号源产生，幅度一定，频率不同，经抗混叠滤波器处理后输入模数转换器，数据经FPGA处理后送入数模转换器，通过示波器观察不同频率下数模转换器输出的幅度。当输入信号为峰峰值5V，频率分别为 500Hz、1.2kHz、2.8kHz、5kHz的正弦波时，数模转换器输出信号的峰峰值对应为0.4V、4.08V、3.52V、0.32V，滤波效果明显。实测结果如图4所示，各图中上方的曲线为滤波器输出结果,下方的曲线为滤波器的输入信号。

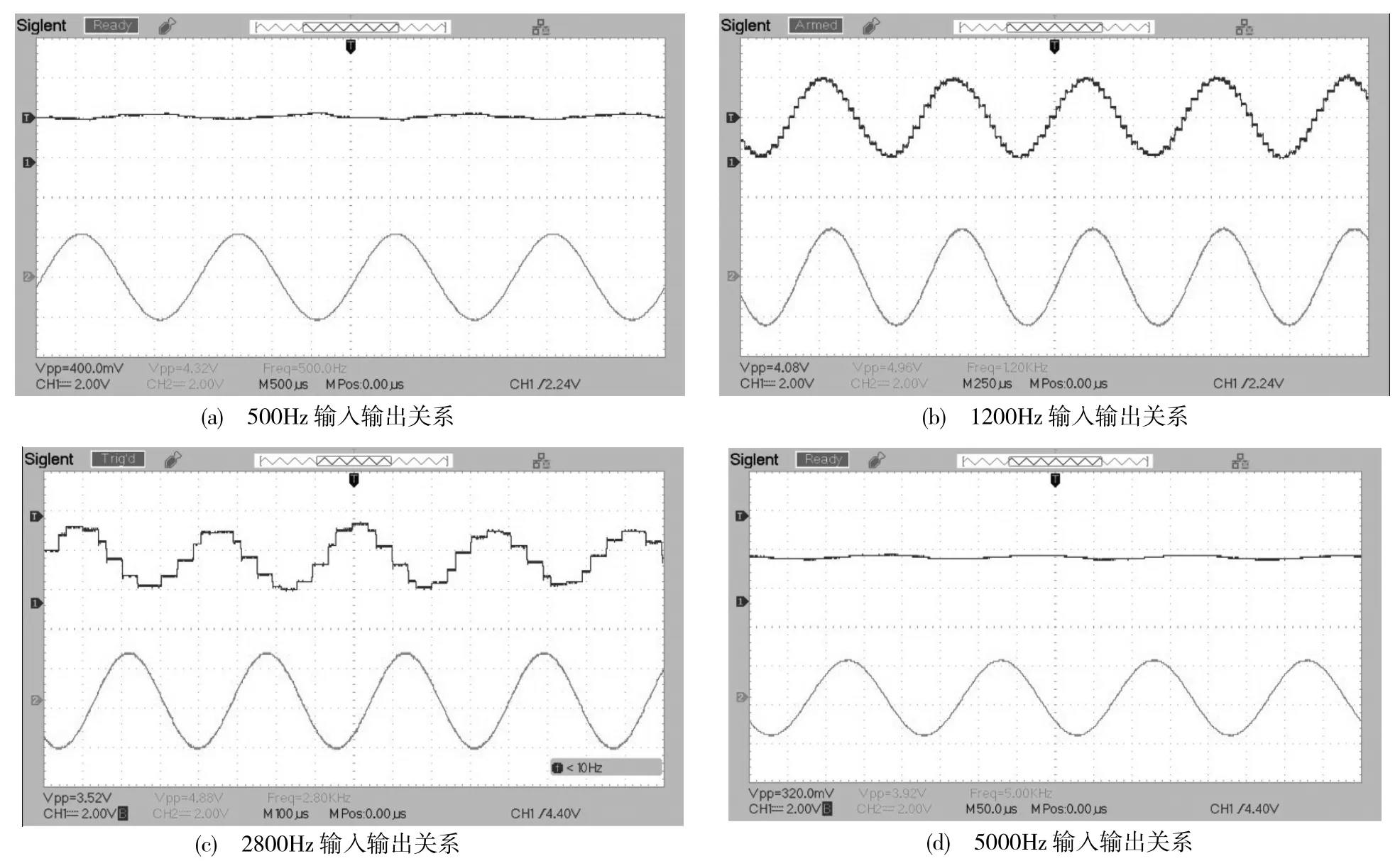
图4 滤波器实际测量结果

模数转换器模拟输入范围正负5V，数模转换器模拟输出范围0至5V，根据输入输出数据的位数可以计算出滤波器实际放大倍数为测量放大倍数的128倍，如下式所示：

将各频点的实测数据带入公式(4)可计算出滤波器的实际增益，由幅频特性曲线可以得出滤波器的理论增益，结果如表2所示。

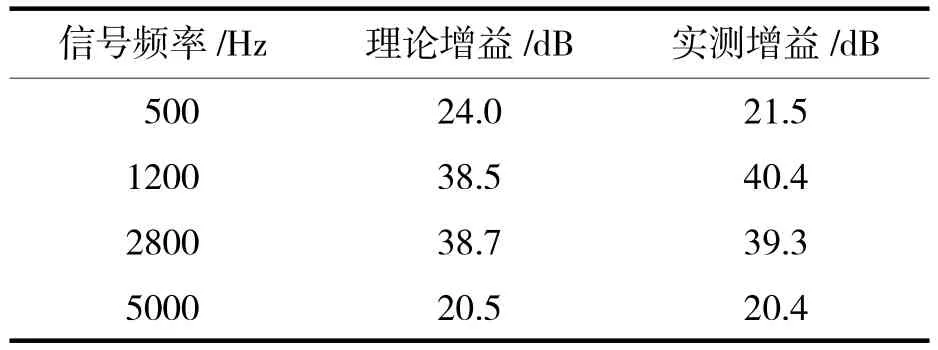
表2 实测结果对比表

实际增益与理论增益有一定的偏差，考虑到抗混叠滤波器对信号的影响，以及示波器读数的误差，实测数据与理论基本吻合，实物测试平台如图5所示。

图5 实物测试

6 结束语

通过试验测量证明了采用建模仿真确定各节点字长的方法是合理的，使用移位及加法代替乘法是可行的。如果需要进一步减小实际与理论的偏差，可以对系数进行进更高位数的逼近。同时，计算部分的字长与加法的级数也会随之增加，计算速度也将受到影响。这就需要根据使用条件的不同，在精度与速度之间取得均衡。

[1]许臣蓉.基于DSP的数字滤波器设计[D].武汉:武汉理工大学,2006.XU Chenrong.Digital filter design based on DSP[D].Wuhan:Wuhan University of Technology,2006.

[2]郭志阳,孙向阳,陈学英.基于FPGA的DSTFT算法对FSK信号解调的改进[J].电子设计工程,2016,24(21):4-6.GUOZhiyang,SUN Xiangyang,CHEN Xueying.Improvement of FSK signal demodulation of DSTFT algorithm based on FPGA[J].Electronic Design Engineering,2016.24(21):4-6.

[3]王大伟,贾荣丛,王划一.基于Matlab的巴特沃斯滤波器设计[J].现代电子技术,2012,35(21):71-72.WANG Dawei,JIA Rongcong,WANG Huayi.Design ofButter worth analog filter based on Matlab[J].Modern Electronics Technique,2012,35(21):71-72.

[4]朱广信.高效数字滤波器结构研究及其在虚拟听觉实现中的应用[D].杭州：浙江大学,2010.ZHU Guangxin.Research on efficient digital filter structure and its application in virtual auditory realization[D].Hangzhou:Zhejiang University,2010.

[5]胡广书.数字信号处理[M].北京:清华大学出版社,2003.HU Guangshu.Digital signal processing[M].Beijing:Tsinghua University Press,2003.

[6]Sait S M,Farooqui A A,Beckhoff G F.A novel technique for fast multiplication[C]//Computers and Communications,1995.,Conference Proceedings of the 1995 IEEE Fourteenth Annual International Phoenix Conference on.IEEE,1995:109-114.

[7]Hashemian R.A new method for conversion of a 2's complement to canonic signed digit number system and its representation[C]//Signals,Systems and Computers,1996.Conference Record of the Thirtieth Asilomar Conference on.IEEE,1996:904-907.

[8]张伟,顾强,李世中,等.基于SignalTap II的数据采集系统设计与调试[J].微型机与应用,2014,33(2):8-10.ZHANG Wei,GU Qiang,LI Shizhong,et al.Design and debugging of the data acquisition system based on SignalTap II[J].Microcomputer&Its Applications,2014,33(2):8-10.

[9]晏勇.基于FPGA三相正弦信号发生器的设计与实现[J].电气自动化,2014,36(4):38-40.YAN Yong.Design and implementation of 3-phase Sinusoidal signal generator based on FPGA[J].Electrical Automation,2014,36(4):38-40.