密码技术在教务管理中的应用研究

李云波

（黑龙江外国语学院,哈尔滨150025）

1 引言

传统的网络安全技术大多针对服务器以及网络的安全，而这样的安全仅能保证服务器在未被外界攻破的情况下进行单纯的安全维护，也就是说在服务器未被攻破的情况下所有保存的数据是安全的，一旦服务器被攻破，那么，所有数据完全的公开在攻击者面前，并且这样的安全维护也不利于非外部攻击的信息泄漏。如何能在外部攻击已经攻破网络防御的情况下保障已有数据的安全性，以及如何防止非外部攻击的信息泄漏问题已成为当前网络信息技术安全研究的一个重要方面。

将通信技术中的密码学技术引入到软件技术、数据库技术为解决该问题带来了希望，然而如何引入以及引入到何种部位，使用密码学技术的哪个方面，应用到何种技术，怎样在不影响系统运行速度的情况下应用该技术，怎样去保障存储的数据的安全具有很强的理论意义和应用价值。因此论文从密码学技术的角度针对现有的教务管理软件的各个方面的安全性进行研究探讨，提出相应的密码算法，解决当前教务管理软件中存在的安全问题。

2 国内外研究现状

密码学是结合数学、计算机科学、电子通信等诸多学科于一体的交叉学科。19世纪的工业革命为使用更加复杂的密码技术提供了条件。密码设计者设计出了一些利用电动机械设备实现信息加密/解密的密码方法，采用电报机发送加密信息[1]。计算机技术的发展，为密码学带来了新的发展方向和发展工具，另一方面也给密码破译者提供了有力的武器。密码学广泛应用是从20世纪70年代中期，源于计算机网络的普及和发展。1977年1月NBS公布了美国的数据加密标准（DES,Data Encryption Standards），并于1997年开始征集高级加密标准AES，2000年采用Rijndael算法作为该标准。数据加密标准DES完全公开了加密、解密算法。使得密码学得以在民用领域广泛应用，从而带来巨大的生命力，得到了迅速的发展。

1976年以前的所有密码系统均属于对称密码学范畴。在1976年，Diffie和Hellman发表了著名的《密码学的新方向》，提出了一个崭新的思想，该思想不仅加密算法本身可以公开，甚至加密的密钥也可以公开，这就是著名的公钥密码体制思想[2]。1978年美国麻省理工学院的Rivest、Shamir和Adleman提出RSA公钥密码体制。这是迄今为止第一个成熟的、最成功的公钥密码体制[3]。此后，人们又相继提出了 Rabin、Elgamal、Goldwasser-Micali概率公钥密码、ECC和NTRU等公钥密码体制。同时，由于近年来其他相关学科的进步和发展，出现了一些新的密码技术，如DNA密码、混沌密码和量子密码等。

3 教务管理数据所对应的密码体制

当今对于密码学技术的应用一般用在通信技术领域，在软件上的应用一般用在对于软件序列号、软件登录加密等较少的几个应用层面。目前尚缺乏对整个应用软件的各个应用部分根据涉密程度进行整体的、系统的加密研究与加密管理。因此，本文针对加密领域的这一空白，从教务管理软件出发研究在整个教务管理软件中各个部分涉及到的不同安全级别，进行相应的密码学技术的应用研究探索。对于教务管理安全的引用研究主要应用以下已提出或应用的密码体制并根据教务数据类型进行尝试探索。

①对称密码体制：对称密码根据加密模式又可分为分组密码和序列密码。分组密码的典型算法有DES、AES、IDEA、RC6、Skipjack 等，序列密码的典型算法有 RC4、A5、SEAL、WAKE、PKZIP 等，针对这两种算法进行分析和比较，在确定数据的保密级别的基础上寻找一个适用的高效的对称密码算法[4]。对教务管理系统中的成绩数据使用AES算法或者其变种，因为成绩在采用秘密保存的同时必须能够顺利的解密，且成绩保存的期限一般不超过六年。

②非对称密码体制：针对教务管理系统中存在多方客户保密信息的录入问题，在公钥密码体制中寻找一种能够由管理人员控制的、安全的录入环境，即由管理人员掌握私钥，在已知的客户端公开公钥，由管理人员确定录入信息的准确性。在应用最广的RSA、ElGamal和ECC等密码体制下，重点使用身份基公钥密码，以客户端身份作为公钥，在教务管理系统中解决身份基公钥体制中公钥管理和应用范围的问题[5]。

③各种密码体制与数据的结合：在选定密码体制时，需要针对已有的数据的保密程度确定使用的密码算法，其中，管理员的密码保护为所有保密级别中的最高级别，采用Hash函数来进行加密，当前的MD5、SHA1、SHA256、SHA512 等 Hash 算法一般称为单向加密，也就是说使用该方法加密后无法解密。研究方案整体思路如图1所示。

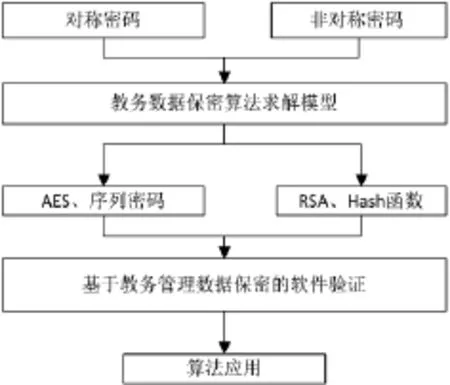
图1 研究方案整体思路

在图1中可以看出，针对教务管理软件的不同应用，方案设计使用与之对应的加密方法，有助于提高教务管理信息安全技术水平，能够有效的保障教务管理数据的信息安全。

4 针对教务数据的密码技术

本文主要研究如何在教务管理系统中使用密码技术，对于不同数据的密码技术选择结果如图2所示。

①保密数据和密码算法选择：在教务管理数据中需要加密的数据主要是用户密码、权限分配管理、敏感数字屏蔽、一般数据处理等几个方面。使用这些数据时根据其保密级别进行分类，分别采取不同的保密形式以及密码算法，其中，根据数据管理和数据类型的差别密码算法的选择也是不同的[6]。在教务管理系统中最高级别的保密是管理员的账户和密码，其次是分级的各个管理账户，即是各用户权限的明确与保密，也就是在客户端进行的与管理员的互动之间的安全保密，例如，教师之间成绩的录入、教师之间评教的操作等。第二是敏感数字的屏蔽，例如成绩、评测结果、个人用户信息等。最后是一般数据的处理，可存储为明码数据。

图2 不同级别的密码算法选择

②密码算法和软件结合：密码算法通常都是使用最简单且行之有效的方法进行加密的，其中一次一密是保证密码算法不被破解的最有效方式，但是，若采用这种方法将会对软件甚至是计算机本身提出更高的要求，若密钥的位数与秘密信息本身位数相同，处理这样的加密计算将耗尽系统资源，在应用中也是不可行的。然而，密码算法本身不够严谨或者算法本身加密作用有限，与明文区别不大，缺乏加密的意义[7]。简单的说，密码算法与软件之间的结合就是在加密效率与软件执行效率之间寻找一个平衡，这个平衡是在软件运行效率与密码加密程度之间的一个行之有效的方法。也就是说，密码算法既不能复杂到影响整个系统的正常运行，导致系统本身因增加加密计算而产生不良后果，又不能简单到起不到加密作用，如：将秘密信息简单的进行字母代换等。

③单向加密恢复：对于最高级别保密权限的管理人员的账户采用单向加密，这样最大限度的对该信息进行了保密，但保密同时也带了一定的问题。首先，管理人员的权限巨大，易造成权利的过分集中；其次，单向加密后的信息是无法通过算法本身进行恢复的，一旦产生不可抗力造成管理人员账户的丢失等情况，系统将存在极大的安全隐患[8]。所以，对于单向加密的恢复应该在既不影响管理人员权限的同时又要适当的限制管理权限，同时，在丢失信息的情况下可以通过一定的手段进行恢复，还要保证恢复是在多数的二级管理人员的同意下进行的。

5 结束语

论文针对教务管理数据的数据安全问题，提出了基于密码技术的能够与相关软件应用相对应的加密解决方案，该方案通过对不同类型教务数据自身特色的分析使用能够有效契合该类数据的基于密码技术的加密方法，有效的保护教务管理系统中保存的数据，能够在系统被攻击或其它情况下保障数据的安全有效，为教务数据的信息安全提供有益的探索。

[1]肖人毅.公钥密码分析简介[J].软件学报,2016,27(3):760-767.XIAO Renyi.Brief introduction of public key cryptanalysis[J].Journal of Software,2016,27(3):760-767.

[2]安吉旺,徐凯宏.基于RSA和密钥的二维码加密编码的研究[J].森林工程.2014(02):125-129.AN Jiwang,XU Kaihong.Research on two-dimensional code encryption based on RSA and key cryptography[J].Forest Engineering.2014(02):125-129.

[3]黄刘生,田苗苗,黄河.大数据隐私保护密码技术研究综述[J].软件学报,2015,26(4):945-959.HUANG Liusheng,TIAN Miaomiao,HUANG He.A review of cryptographic technology for large data privacy protection[J].Journal of Software,2015,26(4):945-959.

[4]徐津,温巧燕,王大印.一种基于Hash函数和分组密码的消息认证码[J].计算机学报,2015,38(4):793-803.XU Jin,WEN Qiaoyan,WANG Dayin.A message authentication codebased on Hash function and block cipher[J].Chinese Journal of Computers,2015,38(4):793-803.

[5]Katz J,Vaikuntanathan V.Round-optimal password-based authenticated key exchange[C]//Theory of Cryptography Conference.Springer,Berlin,Heidelberg,2011:293-310.

[6]CHEN L,MALONE-LEE J.Improved identity-based signcryption[C]//International Workshop on Public Key Cryptography.Springer Berlin Heidelberg,2005:362-379.

[7]Dan B,Lynn B,Shacham H.Short Signatures from the Weil Pairing[J].Journal of Cryptology,2004,17(4):297-319.

[8]Halevi S,Kalai Y T.Smooth Projective Hashing and Two-Message Oblivious Transfer[J].Journal of Cryptology,2012,25(1):158-193.