基于LabVIEW的ARPA跟踪算法仿真系统实现∗

杨瑞容 郑振宇

（1.海军大连舰艇学院学员旅 大连 116018）（2.海军大连舰艇学院航海系 大连 116018）

1 引言

自动雷达标绘仪（Automatic Radar Plotting Aid，ARPA）是一种把雷达技术与计算机应用结合在一起的船舶避碰设备，可连续自动提供需要的航行及避碰信息数据，并对航行态势进行评估。AR⁃PA系统核心算法为目标跟踪算法，其主要目标是建立目标运动轨迹，以提醒指挥员危险目标的运动状态，在跟踪过程中，需要采用有效的滤波算法来消除观测噪声的影响，目前，主流的航海雷达ARPA跟踪算法多都采用α-β滤波及各种改进算法［1］。LabVIEW是一种实验室虚拟仪器集成开发平台，其采用图形化编程语言（G语言），具有编程可视化，界面美观化、开发模块化等特点，是用来开发仿真系统的平台［2］。本文基于LabVIEW开发了一套ARPA跟踪算法仿真系统，并应用经典α-β滤波算法与改进算法进行仿真分析，具有较强的工程应用价值。

2 LabVIEW平台下ARPA算法的实现

2.1 基本设计思路

ARPA采用边扫描边跟踪的方式，雷达记录下目标在屏幕上位置随扫描更新的变化，建立目标的运动轨迹方程，即完成了目标跟踪过程。跟踪器采用跟踪波门按照设定的滤波算法，随着天线旋转扫描，在波门内部检测到目标的存在，记录下目标位置，驱动波门预测目标运动轨迹。波门采用可变波门，即分为大、中、小三种。在LabVIEW平台下通过定时控件按照舰船运动模型输出经纬度序列，添加杂波干扰滤除技术模拟生成目标运动序列数据。采用α-β滤波算法建立目标的预测跟踪，根据预测目标与实测目标的距离获得预测误差，根据预测误差的大小来确定波门大小，若采用大波门连续5次未录取到目标，则视为目标丢失，发出报警信号。

2.2 功能模块

程序功能模块主要包括舰船目标运动模型、α-β滤波器、波门设计、态势显示以及其它辅助功能设计。

1）舰船目标运动模型

该模型是通过定时输出一组二维数据来模拟目标的位置。采用LabVIEW公式节点控件建立运动模型，输入目标的初始位置、初始航向、初始航速的参数，并且建立杂波仿真模型，模拟杂波对雷达造成的观测误差，通过定时控件和移位寄存器等时间间隔输出目标的实时位置，运动模型参数如表1所示。

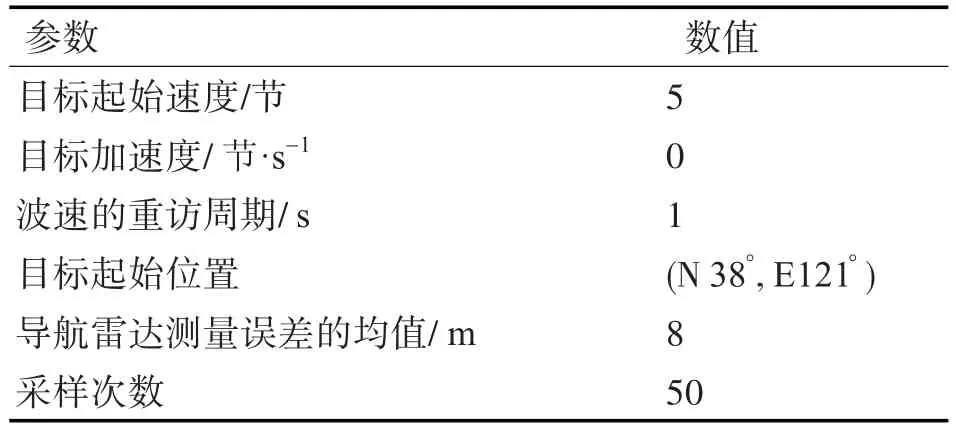
表1 匀速目标运动模型输入数据参数信息

2）α-β滤波器

通过在LabVIEW平台内嵌Matlab脚本文件节点实现α-β滤波器算法功能。Matlab脚本节点可提高运算效率，并且可通过改变在脚本节点内需要输入的具体执行语句就能转换为其它类型的滤波器，从而实现滤波器的转换功能。

3）波门设计

波门设计在本程序中的主要思路是通过读取跟踪目标下一时刻的预测位置，然后以该位置为波门的中心，根据上一时刻跟踪目标的实测位置与预测位置的距离差来确定波门宽度，实现跟踪系统当中反馈环节的功能。本文设计的波门有圆形波门和方形波门，并且将波门分为大、中、小三种，若目标的预测误差超过10m，则采用大波门，若预测误差在5m～10m之间或前25个采样点均使用中波门，若预测误差小于5m，则采用小波门。

4）态势显示

图1为合并信号控件图示与态势显示的程序框图。

通过合并信号控件将目标的实测轨迹、预测轨迹、平滑轨迹以及波门都同时显示在XY图上。由于目标的运动是实时更新的，因此为了使目标能一直直观地显示在XY图上，并能看出目标之前一段时间的航迹，增强软件的实用性，该程序对其的设计是，对于前二十个采样点，即从目标开始录取的前20s，XY图的显示区域的经度范围为E121°～E121.0005°，纬度范围为 N38°～N38.0005°，之后XY图的显示区域是为以波门中心设为(j，w)位置为中心，则经度的显示范围为E(j-0.00025)°～E(w+0.00025)°，纬度的显示范围为 N(w-0.00025)°～N(w+0.00025)°。

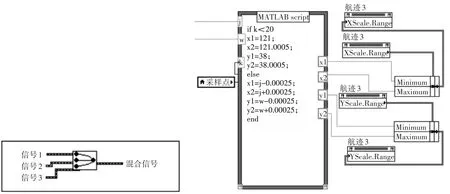
图1 合并信号控件图示与态势显示程序框图

5）其它辅助功能

本程序中的辅助功能主要是给ARPA系统添加报警功能，通过设计一个变量p，初值为0，当采用大波门而未录取到目标时（即预测误差大于波门宽度时），p值加1，若下一时刻采用大波门仍未录取到目标，则p值再加1，否则p值清零。当p值为5时（即采用大波门连续5次未录取到目标），输出报警信号q，值为5，此时p值清零。最后通过布尔控件在前面板上显示为红灯报警。

3 α-β滤波算法仿真分析

在对α-β滤波算法进行仿真测试时（选用圆形波门），以目标的起始位置为坐标原点建立平面直角坐标系，对目标的初始运动参数进行设定。根据船用雷达设备推荐性能标准，采用雷达对目标进行距离测量时，其误差不超过所用量程的1.5%或70m，取其最大者［3］。滤波器真正起作用的是从第3个采样点开始的，因此对误差的统计从第3个点开始。

3.1 常增益α-β滤波算法

常增益α-β滤波算法中有最优选择法、稳态卡尔曼增益选择法、卡尔曼增益选择法、临界阻尼选择法和最佳阻尼增益选择法，本文选取最优选择法进行仿真。

α 的 值 分 别 取 0.1、0.3、0.5、0.7、0.9，根 据可得相应的β值。其仿真效果如图2所示，目标预测位置误差的统计如表2所示。

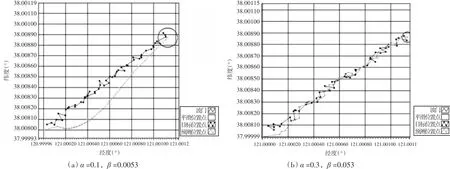
图2 采用最优选择法目标的实测位置与预测位置示意图

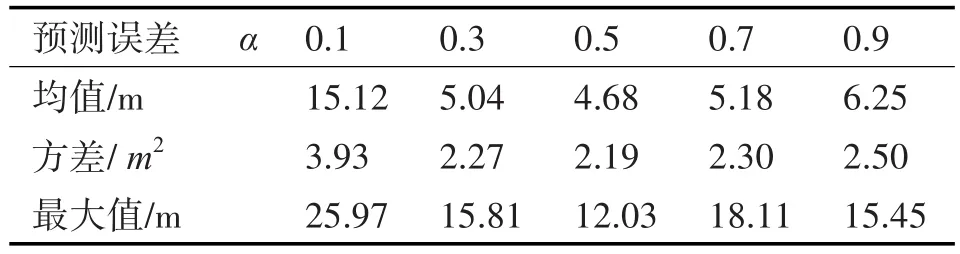
表2 采用最优选择法目标预测位置误差的统计性能

由表2可得出，若α，β的取值越大，跟踪系统的闭环带宽值越大，因此在目标跟踪的初始阶段，系统可以较快地跟踪上目标，但是滤波器的滤波效果差；若α，β的取值越小，跟踪系统的闭环带宽越窄，因此在目标跟踪的初始阶段，目标预测位置的误差大，容易跟踪目标失败，但是其稳定阶段滤波器的滤波效果好。因此对于常增益α-β滤波器，α，β的取值要适中，一般α的取值为0.5较为合适。

3.2 自适应α-β滤波算法

在工程中，常用的自适应滤波算法就是将α，β的值与滤波器的采样序列的数（即本文当中的k值）相关联，从而达到自适应的效果。一种常用的自适应α-β滤波算法，其α，β的取值为

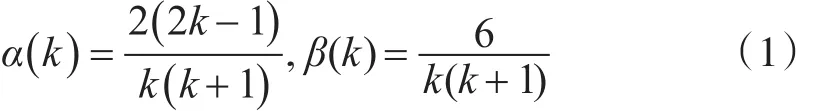
目标预测位置误差的统计性能如表3所示。

表3 采用自适应α-β滤波算法目标预测位置误差的统计性能

由表3可看出，自适应α-β滤波算法明显优于常增益α-β滤波算法，其既能在系统跟踪目标的初始阶段能够快速地跟踪上目标，且整个跟踪过程滤波器的滤波性能较好。

3.3 α-β滤波算法的局限性

α-β滤波算法只适用于匀速运动目标模型，一旦目标突然发生机动，α-β滤波算法的滤波性能将会大大下降，以下分别从两种情况考虑目标发生机动对α-β滤波算法的影响，其中采用常增益α-β滤波算法当中的最优选择法（α=0.5，β=0.17）和自适应α-β滤波算法对其进行仿真与分析。

1）变向目标运动模型

采用α-β滤波算法对变向目标运动模型进行仿真时，其目标的输入参数数据如表1所示，其中采样次数取100，设目标在第50个采样时突然向右打舵，舵角为5°，在第55个采样点时回舵，并利用Matlab画出其预测误差分布图，如图3所示。

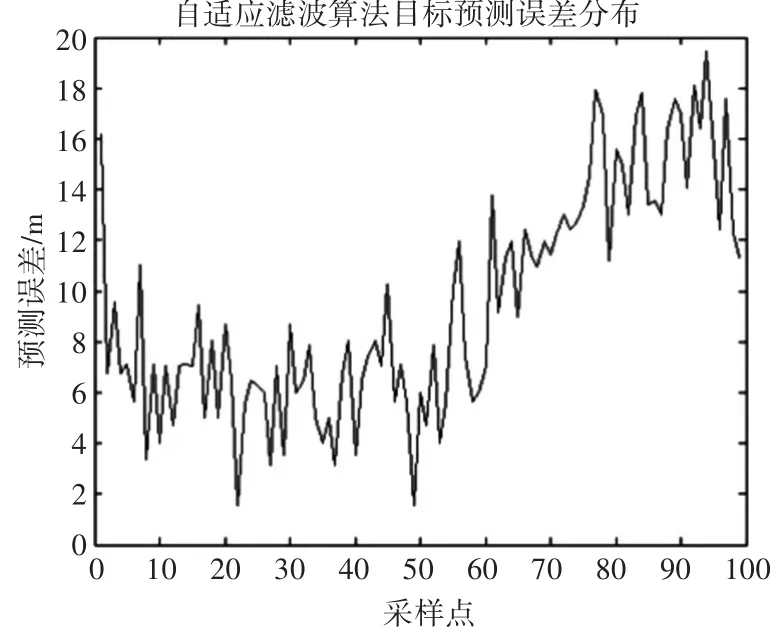
图3 对于变向目标运动模型采用自适应滤波法目标的预测误差分布图

由图3可知，对于变向目标运动模型，采用自适滤波器的滤波性能明显变差。因为自适应滤波器跟踪目标进入稳定阶段后，α，β的值都趋近于0，一旦目标发生转向，目标的预测位置偏离实测位置越来越远，从而使误差越来越大。

2）变速目标运动模型

采用α-β滤波算法对变速目标运动模型进行仿真时，其目标的输入参数数据如表1所示，设做匀速运动的目标在第50个采样点时加速度为1节·s-2，到第65个采样点时加速度为-1节·s-2，到第80个采样点时加速度为0。利用Matlab画出其预测误差分布图，如图4所示。

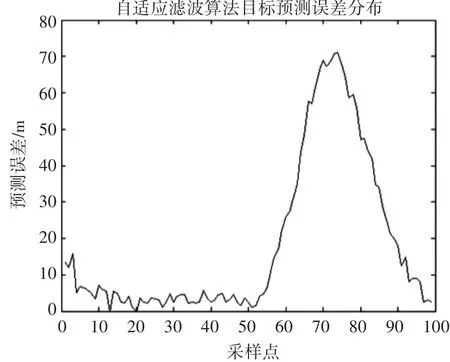
图4 对于变速目标运动模型采用自适应滤波法目标的预测误差分布图

根据上述对自适应α-β滤波器的仿真，可得出当系统跟踪目标进入稳定阶段后，若目标发生机动，其滤波器的滤波性能就开始变差，且预测误差越来越大。最主要归因于式（1）中 α(k)，β(k)的取值方法，随着采样序列的增加，α，β的值都趋近于0，跟踪系统的带宽变得太小，目标一发生机动，滤波器就会丢失目标，因此对该滤波算法进行改进。

我们对自适应α-β滤波器的α，β赋予限定条件，随着采样序列的增加，α，β的值不会趋近于0，而是到达一个最小值，使系统保证有足够的带宽，这样在目标跟踪的稳定阶段，就算目标发生机动，目标跟踪算法也不会发散。当采样序列k≤30时，α(k)，β(k)的取值与式（1）一致，当采样序列k＞30时，α(k )给一个定值，取0.13，β(k)的值根据得，β(k)=0.009，具体表示如下：

由图4可得，对于变速目标运动模型，自适滤波器的滤波性能明显变差。因为自适应滤波器跟踪目标进入稳定阶段后，α，β的值都趋近于0，导致系统跟踪目标主要依赖于目标预测位置，一但目标突然做高加速运动，目标的预测位置偏离实测位置越来越大，从而使误差越来越大。

综上分析，对于机动目标运动模型，自适应滤波器的滤波性能无法满足实际应用中的需求。

3.4 α-β滤波算法的改进

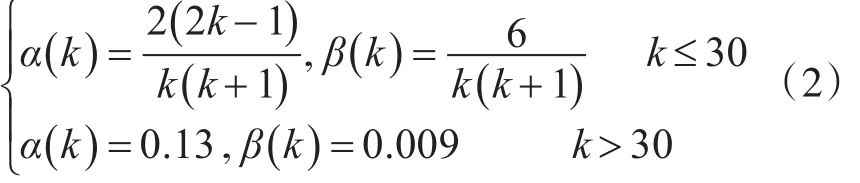
下面分别从变向目标运动模型和变速目标运动模型两种情况进行验证，为了方便进行对比，其初始输入参数信息与表1一致，且在目标转向和目标做加速运动的时间都分别和上述仿真实验完全一致。利用Matlab画出其预测误差方差分布图，如图5所示。

由图5可看出，改进后的自适应α-β滤波器在目标做机动运动时，其滤波器的性能明显得到改善，说明这种改进方法是可行的。对于机动性大的目标，α(k)、β(k)最小值应该取大些，对于机动性小的目标，α(k)、β(k)最小值应该取小些。

4 结语

本文基于LabVIEW平台下完成α-β滤波算法的实现，并阐述了整个程序的编译过程。然后，在此程序下对各个α-β滤波算法进行仿真，得出的结论是对于常增益α-β滤波器，α的取值在0.5附近，即滤波器对目标的实测位置和预测位置的可信度相当时，其滤波器的性能是最优的，目标预测误差最小。在匀速运动目标模型下，自适应α-β滤波器的性能要优于常增益α-β滤波器。然后对自适应α-β滤波器分别在变向目标运动模型和变速运动目标模型下进行仿真分析，得出的结论是，在目标做大幅度机动时，自适应α-β滤波器的性能大大降低。最后对自适应α-β滤波器进行改进，让α，β的值即使在滤波器进入稳定跟踪状态后也不趋近于零而是达到一个最小值，使系统保证有足够的带宽，这样在目标跟踪的稳定阶段，就算目标发生机动，目标跟踪算法也可以适用。通过仿真分析其目标预测误差，验证了此改进方法是可行的，这种算法的改进为开展导航雷达目标跟踪算法的研究提供了技术支持，具有较强的工程应用价值。

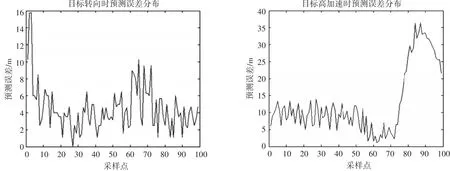
图5 对于两种模型采用改进自适应α-β滤波算法目标预测误差示意图

［1］董小兵，张润泽.自适应α-β滤波在雷达录取跟踪系统中的应用［J］. 大连海运学院学报，1986，1（12）：66-72.

［2］章佳荣，王璨，赵国宇.精通LabVIEW虚拟仪器程序设计与案例实现［M］.北京：人民邮电出版社，2013.

［3］王世远.航海雷达与ARPA［M］.大连：大连海事大学出版社，1998.

［4］何友，修建娟，关欣等.雷达数据处理及应用（第三版）［M］.北京：电子工业出版社，2013.

［5］王红亮，李枫，赵亦工.一种机动目标跟踪的自适应α-β滤波算法［J］. 雷达科学与技术，2007，5（4）：278-291.

［6］杨常青，郑振宇.导航雷达与电子海图［M］.大连：海军大连舰艇学院，2010.

［7］吕昆.雷达目标跟踪算法的应用研究［D］.西安：西安电子科技大学，2012.

［8］ARM 公司 Cortex-M3用户指导用书［EB/OL］.2009：1-9.

［9］穆晔.船用导航雷达ARPA跟踪算法研究［D］.上海：上海交通大学.2007.

［10］张巧丽.基于LabVIEW的运动目标跟踪算法研究与实现［D］.西安：陕西科技大学，2015.

［11］何振亚.自适应信号处理［M］.北京：北京科学出版社，2002.

［12］费业泰.误差理论与数据处理［M］.合肥：合肥工业大学，2015.

［13］张明友，汪学刚.雷达系统（第二版）［M］.北京：电子工业出版社，2006.

［14］丁鹭飞，耿富录.雷达原理［M］.西安：西安电子科技大学出版社，1997.

［15］周宏仁，敬忠良，王培得.机动目标跟踪［M］.北京：国防工业出版社，1991.