一种基于改进支持向量机的目标威胁估计方法

井胜勇

（中国人民解放军国防大学十五队 北京 100091）

1 引言

目标威胁估计在信息融合模型中处于第三级，属于高级信息融合［1］。早在20世纪70年代，美国就开始了信息融合方面的研究。历经多年的发展，欧美等国已研发了许多性能优异的信息融合系统。相比于国外，国内对多传感器信息融合，尤其是有关态势估计和威胁估计等高级信息融合的研究相对较浅，离实战应用相差甚远。

常用于目标威胁估计的方法有直觉模糊集［2］、贝叶斯推理［3］、模糊聚类［4］、Elman-AdaBoost［5］、粗糙集理论［6］、层次分析法［7］、小波神经网络［8］等，但这些方法相对复杂，其结果受各模型内部因素权值影响较大，需要由专业人员根据经验来设定、调整模型参数，带有一定的主观性。此外，这些方法对作战环境的适应性不强，其适用性也相对不足。

支持向量机（Support Vector Machine，SVM）［9～10］是一种基于统计学习理论的机器学习算法，它以结构风险最小化为原则，较好地解决了小样本、非线性和高维数的复杂问题。文献［11］采用SVM对目标威胁估计问题进行了研究，取得了较好的估计结果。但是，SVM在应用过程中，其中的惩罚参数c和核函数参数g的确定仍是难点。粒子群优化算法（Particle Swarm Optimization，PSO）［12～13］是一种群体智能优化算法，已经成功应用在目标跟踪、误差补偿及参数辨识等工程实践中。因此，本文提出了一种改进的支持向量机算法（PSO-SVM），该算法采用粒子群优化算法对SVM中的惩罚参数c和核函数参数g进行优化，以支持对目标威胁的估计。本文首先基于PSO-SVM算法建立了目标威胁估计模型，然后提出了PSO-SVM目标威胁估计算法，最后，对PSO-SVM算法进行了仿真实验。

2 PSO-SVM算法基本原理

2.1 PSO算法基本原理

PSO算法是由Kennedy和Eberhart最早提出的，其思想来源于自然界中鸟类的捕食行为，是一种用于求解最优化问题的方法。PSO算法在可解空间中初始化一群粒子，每个粒子都代表一个潜在解，每个粒子都有一个适应度值，这个值由适应度函数（目标函数）决定。群粒子的属性由位置、速度和适应度值表示。粒子在解空间中运动时，通过个体极值Pbest和群体极值Gbest来动态更新个体位置，从而使得个体在可解空间中达到最优位置。

假设在一个D维的搜索空间中，种群X=(X1，X2，…，Xn)由 n个粒子组成，其中第 i个粒子表示为一个 D 维的向量 Xi=(xi1，xi2，…，xiD)。Xi既表示第i个粒子在D维搜索空间中的位置，也表示该优化问题的一个潜在解。设定粒子i的速度 为 vi=(vi1，vi2，…，viD) ，其 个 体 极 值 为Pi=(Pi1，Pi2，…，PiD) ，种 群 的 全 局 极 值 为Pg=(Pg1，Pg2，…，PgD)，则在每次迭代中，粒子根据个体极值和全局极值更新自身速度和位置的方式如式（1）和式（2）所示。

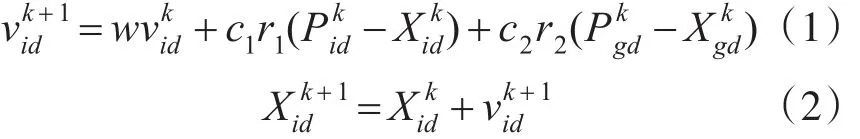
其中，k为当前迭代次数，d=1，2，…，D ，i=1，2，…，n，ω为惯性权重，c1和c2为非负常数，称为加速度因子，r1，r2∈[0，1]，为随机数。

2.2 SVM基本原理

支持向量机SVM算法是由Cortes和Vapnik最早提出的，其主要思想是寻找各样本之间的最大间隔超平面。SVM是一种基于核函数的方法，它通过核函数把特征向量映射到高维空间，然后建立一个线性判别函数，使得满足样本数据的分类间隔最大，从而使得结构风险最小化。SVM的体系结构如图1所示。

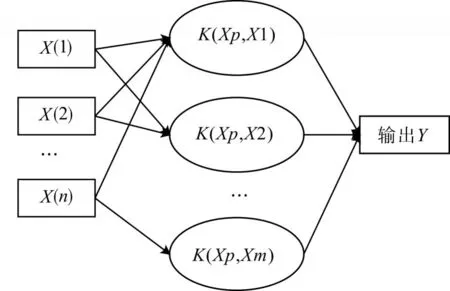
图1 SVM体系结构

在SVM的实际使用过程中，通过引入核函数，将样本数据从低维空间转化到高维空间中，然后再寻找最佳分类超平面。核函数接受两个低维空间的向量，计算经过某种转换后在高维空间里的向量内积值，其一般形式如式（3）所示，其中，φ是低纬空间到高维空间的映射函数。

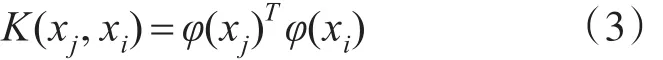
若仍无法找到最优分类超平面将数据完全划分，可通过引入松弛变量，增加对样本数据噪声的容错性，来有效处理高维空间中离群点，以获得允许小部分数据错误划分的相对最优分类超平面。在样本线性不可分的情况下，寻找最优化的分类超平面的问题可转化成如式（4）所示的表达式。

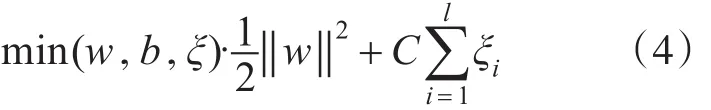
其中，约束条件为

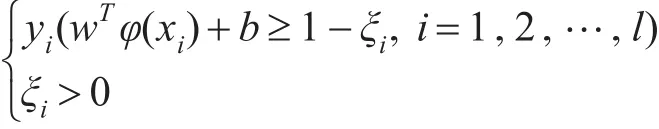
3 PSO-SVM目标威胁估计模型

从计算复杂度方面考虑，目标威胁估计是一个非确定性多项式困难（Non-deterministic Polynomi⁃al hard，NP-hard）问题，需要考虑很多因素，如地理环境，天气情况，敌、我、友军的兵力部署等。本文选取了6个典型指标，用以建立PSO-SVM目标威胁估计模型。在此基础上，本文进一步提出了基于PSO-SVM的目标威胁估计算法。

3.1 目标威胁估计因素

本文进行目标威胁估计时，主要考虑以下6个主要因素：

1）目标类型：表示为小型目标（如巡航导弹）、大型目标（如歼击轰炸机）和直升机；

2）目标速度：表示为 200m/s、1500m/s、260m/s等；

3）目标航向角：表示为10°、21°、60°等；

4）目标干扰能力：表示为强、中、弱、无；

5）目标高度：表示为低、超低、中、高；

6）目标距离：表示为100m、300m等。

3.2 PSO-SVM目标威胁估计模型

本文根据上述目标威胁估计因素而构造的PSO-SVM目标威胁估计模型，其中，输入层的输入为目标类型、目标速度、目标航向角、目标干扰能力、目标高度和目标距离这6个目标威胁估计指标，输出层的输出为当前指标下的预测目标威胁值。

3.3 PSO-SVM目标威胁估计算法

PSO-SVM目标威胁模型在实现过程中一般包括数据预处理、PSO-SVM网络构建、PSO-SVM网络训练、PSO-SVM网络测试等4个步骤，如图2所示。其中，数据预处理完成原始数据的量化、数据的归一化和可视化，得到训练数据集合测试数据集；PSO-SVM网络构建首先通过交叉验证选择最优的惩罚参数c和核函数参数g，然后构建最优PSO-SVM网络以对数据进行训练；PSO-SVM网络训练则通过训练数据集对构建的PSO-SVM网络进行训练，使得模型最优；最后，PSO-SVM网络测试利用测试数据集对训练得到的PSO-SVM网络进行预测，检验模型的有效性和准确率。

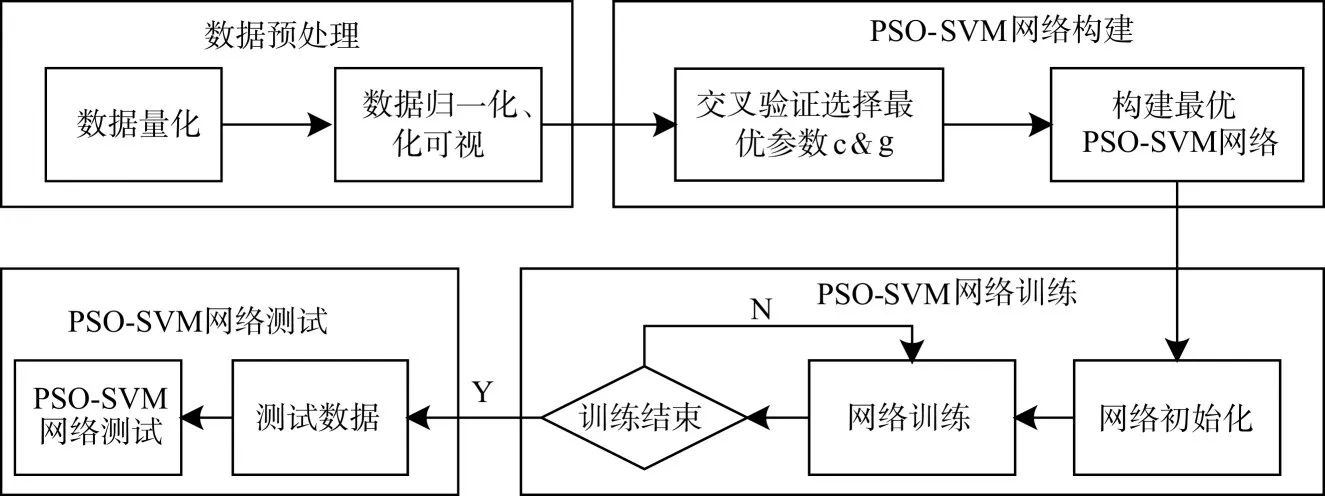
图2 PSO-SVM模型整体流程

本文的主要工作是在图2的PSO-SVM网络构建过程中，在交叉验证选择最佳参数惩惩罚参数c和核函数参数g时，引入了PSO算法进行寻优，其具体过程如图3所示。在图3中，初始化种群和速度为粒子初始位置和速度赋予随机值，然后利用SVM训练函数计算粒子的适应度值，再根据新种群中粒子适应度值确定个体极值和群体极值，最后，根据式（1）和式（2）更新粒子的速度和位置。

4 仿真实验

本节将通过仿真实验对本文提出的PSO-SVM目标威胁估计方法进行验证。

4.1 仿真数据预处理

本文随机选择75组原始数据作为威胁目标，其中，大型目标、小型目标和直升机各25组，训练集中大型目标、小型目标和直升机各20组，剩余15组数据则作为测试集。部分原始仿真数据如表1所示。

本文对上述指标中的非数字化指标分别做如下处理：

1）目标类型：大型目标、小型目标、直升机依次量化为3、2、1；

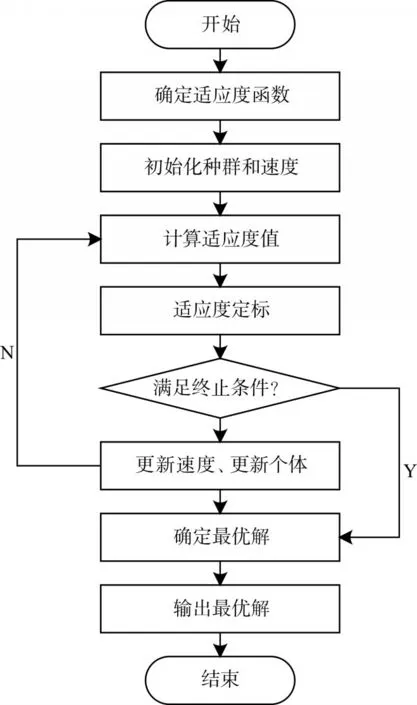
图3 利用PSO优化SVM参数流程

2）目标干扰能力：如强、中、弱、无依次量化为3、2、1、0；

3）目标高度：如超低、低、中、高分别量化为0、1、2、3。

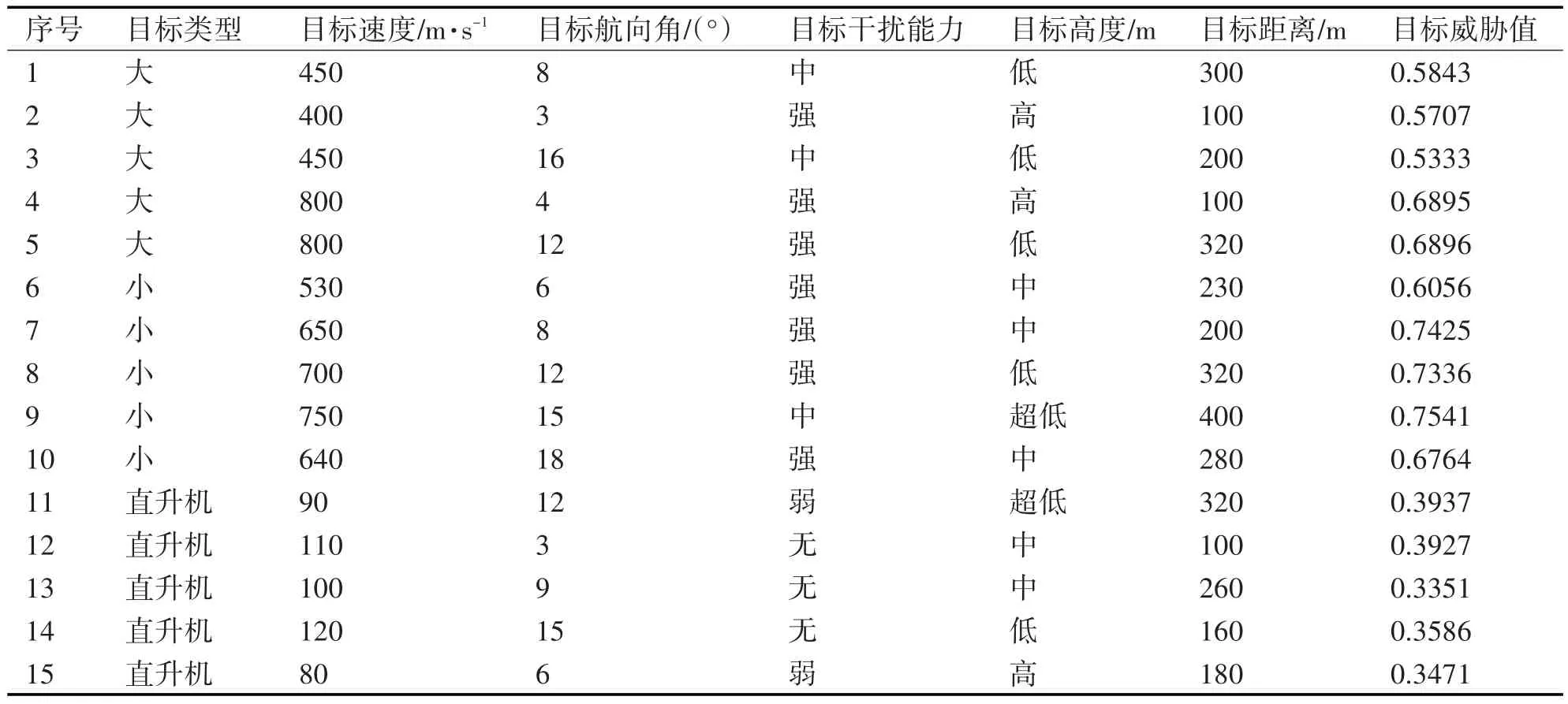
表1 部分原始仿真数据

对于指标中的目标速度、目标高度和目标距离则直接进行归一化，然后转化为PSO-SVM模型能够识别的输入形式。对数据集进行量化后，再进一步对训练集和测试集进行［0，1］归一化处理，其归一化映射为

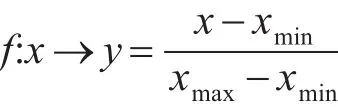
其中，x，y∈Rn，xmin=min(x)，xmax=max(x)。归一化后原始数据将被规整到［0，1］内，即xmin，xmax∈[0，1]。

4.2 仿真结果与分析

本文在一台CPU为Intel 4590 3.3GHz、内存为2048M的机器上，利用LIBSVM软件包实现了本文的PSO-SVM目标威胁估计算法，其中，LIBSVM使用的是默认的C-SVR和RBF核函数，即C=1，g=1/n。

本文具体的仿真过程为：将目标威胁数据读入，经过预处理后，转为LIBSVM软件包能够识别的类型。交叉验证选择参数时，采用PSO算法进行优化，以确定最优的惩罚参数c和核函数参数g。默认情况下，PSO局部搜索能力为c1=1.5，全局搜索能力为c2=1.7，最大进化次数为maxgen=200，最大种群数为sizepop=20，弹性系数ωv=1，SVM的惩罚参数参数c的最大值和最小值分别为100和0.1，SVM的核函数参数g的最大值和最小值分别为1000和0.01。PSO算法将返回最优的MSE和参数c与 g如下：bestmse=0，bestc=20.7043，bestg=652.1897。训练集的仿真结果如图4所示。

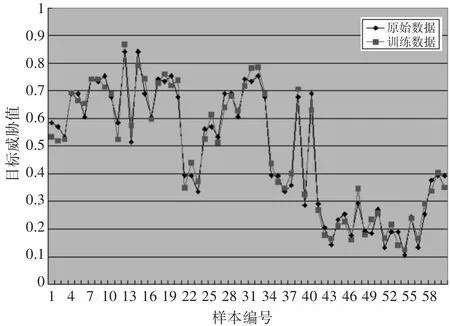
图4 PSO-SVM训练集数据和原始数据对比

4.3 实验分析

本小节将对比SVM仿真结果和采用PSO算法进行参数寻优的SVM仿真结果。SVM的整体流程与PSO-SVM相同，都是采用训练集训练SVM，再用训练集测试训练结果，最后对测试集进行预测。本文将SVM和PSO-SVM的仿真程序都运行10次，其结果分别如表2和表3所示。

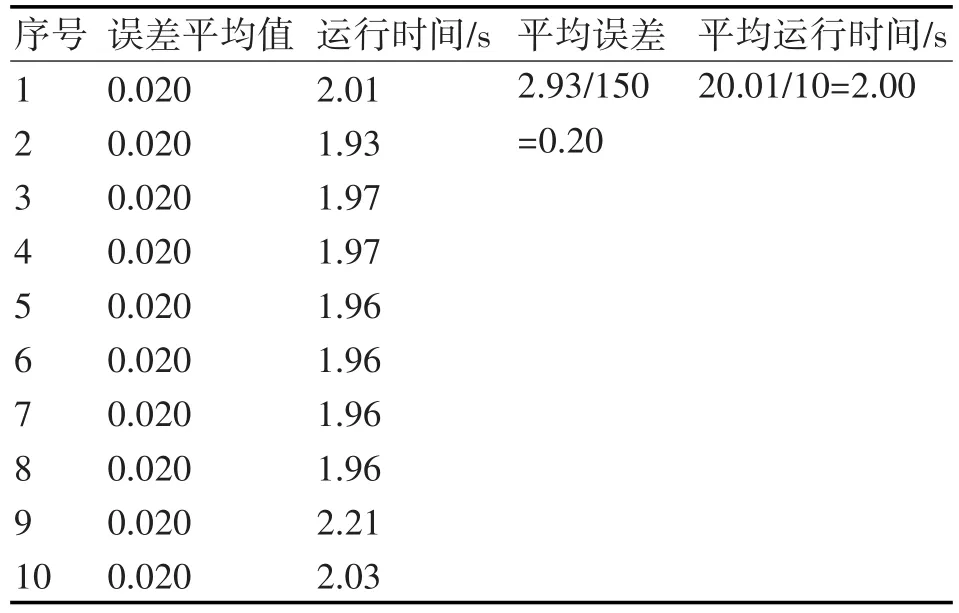
表2 SVM仿真结果

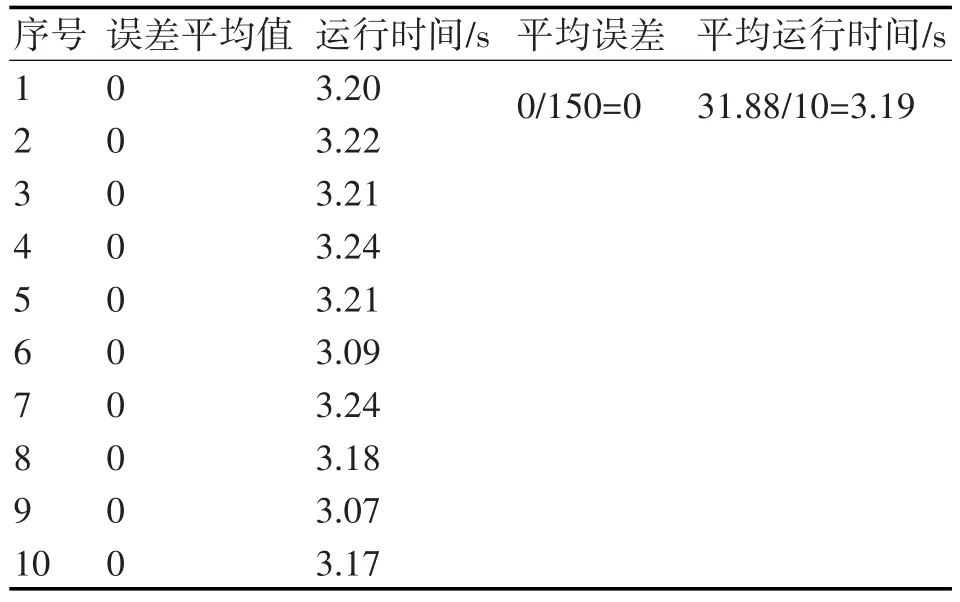
表3 PSO-SVM仿真结果

由表2和表3可以得出，对于目标威胁估计问题，PSO-SVM的预测误差要远小于SVM，但比SVM要耗费更多的时间，这主要是因为PSO-SVM在交叉验证寻找最优惩罚参数c和核函数参数g时需要耗费较多的时间。如果不考虑寻找最优参数所用的时间（即PSO-SVM网络训练时直接给出最佳参数c和g），则PSO-SVM和SVM算法所用时间相差不大，可满足实际应用的要求。

5 结语

针对现代战争对信息获取和处理的需求，在综合考虑信息融合中目标威胁估计的特点和目标威胁值的主要影响因素的基础上，本文提出了一种基于改进支持向量机（PSO-SVM）目标威胁估计方法。本文建立了PSO-SVM目标威胁估计模型，实现了PSO-SVM目标威胁估计算法，并对该方法进行了仿真实验。仿真实验结果显示，本文算法的平均误差绝对值为零，远远优于普通的SVM算法，具有很好的预测能力，可以快速、准确地实现作战目标威胁估计。在未来工作中，还可从实时性的角度将本文方法与其他方法（比如遗传算法，蚁群算法，神经网络等）进行比较，同时，还可采用其他数据集（如UCI数据集）对本文提出的PSO-SVM目标威胁模型进行测试，以分析和验证其实用性和普适性。

［1］J.Linas，D.L.Hall.An introduction to multisensor data fu⁃sion［C］//Proceedings of the 1998 IEEE International Symposium on Circuits and Systems，1997：6-23.

［2］杨健，高文选，刘军.一种基于贝叶斯网络的威胁评估方法［J］.解放军理工大学学报：自然科学版，2010，11（1）：43-48.

［3］姚磊，王红明，郑锋，等.空中目标威胁估计的模糊聚类方法研究［J］.武汉理工大学学报（交通科学与工程版），2010，34（6）：1159-1162.

［4］王改革，郭立红，段红，等.基于Elman-AdaBoost强预测器的目标威胁评估模型及算法［J］.电子学报，2012，40（5）：901-906.

［5］罗艳春，郭立红，李念峰，等.粗集理论在空中目标威胁等级判断中的应用［J］.计算机工程与应用，2009，45（10）：231-234.

［6］谷向东，童中翔，柴世杰，等.基于IAHP和离差最大化TOPSIS法目标威胁评估［J］.空军工程大学学报（自然科学版），2011，12（2）：27-31.

［7］邓雪，李家铭，曾浩健，等.层次分析法权重计算方法及其应用研究［J］.数学的实践与认识，2012，42（7）：93-100.

［8］左东广，周帅，张欣豫.小波神经网络［J］.兵器装备工程学报，2012，33（5）：84-86.

［9］丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究综述［J］.电子科技大学学报，2011，40（1）：2-10.

［10］梁礼明，钟震，陈召阳.支持向量机核函数选择研究与仿真［J］.计算机工程与科学，2015，37（6）：1135-1141.

［11］郭辉，徐浩军，刘凌.基于回归型支持向量机的空战目标威胁评估［J］.北京航空航天大学学报，2010，36（1）：123-127.

［12］夏立荣，李润学，刘启玉，等.基于动态层次分析的自适应多目标粒子群优化算法及其应用［J］.控制与决策，2015（2）：215-221.

［13］谢承旺，邹秀芬，夏学文，等.一种多策略融合的多目标粒子群优化算法［J］.电子学报，2015，43（8）：1538-1544.