基于航空反潜战术搜索确定区域的优化方法

郑润高 张成栋

（海军蚌埠士官学校 蚌埠 233012）

1 引言

由于现代潜艇的威胁正在不断增长，反潜战作为潜艇战的反制措施，正在受到各海军国家的普遍重视。目前，世界各国海军的大、中型反潜水面舰艇普遍装备有反潜直升机。舰载直升机反潜已成为现代水面舰艇反潜的重要手段。航空反潜以其快速反应能力强、搜潜效率高、隐蔽安全、攻潜效果好等优势而成为反潜的主力军。航空反潜主要由搜索和攻击两部分行动组成，而对潜艇的搜索是关系到反潜作战成败的首要环节［1］。因此，科学组织搜索行动、提高搜索效率的重要性不言而喻。为研究方便，本文假定反潜活动方式为应召反潜。

2 一般的航空反潜搜索区域确定模型［1］及其不足

2.1 一般的航空反潜搜索区域确定模型

应召反潜搜索区［2］通常根据发现目标的初始位置、判断敌潜艇可能使用的航速（v潜）、从发现潜艇到飞机到达发现目标的初始位置所用的总时间（t总）、反潜飞机搜索所用时间（t搜）等因素来确定。

其中，t总=t报+t决+t传+t准+t航。 t报为最初发现潜艇并报告指挥所经过的时间；t决为指挥员定下决心所用时间；t传为传达命令所用时间；t准为反潜飞机出动准备所用时间；t航为反潜飞机飞抵目标初始发现点所用时间。反潜飞机搜索范围的大小为

图1 确定应召反潜搜索区示意图

2.2 模型存在的不足

现代信息化战争中战场环境瞬息万变，战斗行动效率将直接影响战斗结果。在反潜搜索行动中，搜索区域的确定是搜索行动的第一步，对于搜索结果有着重要影响。上述搜索区域确定模型虽然在理论上讲完全符合作战要求，但是从实战角度来说还存在着以下两个方面的不足：

一是搜索区域没有轻重主次之分。我们知道在一定条件下的一定时间内潜艇活动具有一定的连续性，比如在目标潜艇尚未发觉我方发现其行踪时，它的行动轨迹、速度、状态、航向等均不会发生急剧变化。因此，在一定时间内，确定反潜飞机搜索范围应当充分考虑这些因素。上述模型从理论上虽然完全覆盖了目标潜艇存在的范围，但忽略了潜艇存在区域的差别性和规律性。对某些区域来说，目标潜艇存在的可能性很小或者根本就不可能存在。这种“顾全”的搜索思路可能会影响整个反潜行动的效率，延长反潜搜索时间，延误最佳搜索时机。

二是搜索区域的确定缺乏动态性。在反潜搜索行动中敌我双方均在动态变化，所以搜索区域的确定在充分考虑轻重主次的基础上还应该考虑彼此动态变化这一重要特点。依上述模型，以磁力探测仪搜索中的圆形搜索方法为例[1]，反潜飞机搜索路径为圆形，其半径主要取决于敌潜艇可能使用的速度（v潜）和发现到开始搜索的时间间隔（t），计算公式为：R=v潜⋅t，得到的搜索区域是一个固定的圆形区域。而在实战中，按照半径R(t)=v潜⋅f(t)计算公式所进行的搜索效率比较理想。

3 航空反潜搜索区域分析与优化

3.1 搜索区域确定方法的优化

为研究方便，我们给出了如下一些变量及其意义说明：vmax为目标潜艇最大可能航速，判断依据来源于战前对目标潜艇情报的搜集；vmin为目标潜艇最小可能航速，判断依据为目标潜艇为达到一定战术目的所做的战术调整（如低速航行降噪），0≤vmin≤v潜；v潜为初始位置时刻目标潜艇航速，若搜索行动开始前仍无法确定目标潜艇航速，则令v潜=vmax；φ为初始位置时刻判断的目标潜艇航向，搜索行动开始前仍无法确定时以发现点至我方连线角度进行赋值替代。在搜索行动中，可依据获取的实际信息重新进行赋值；t总为同上，即t总=t报+t决+t传+t准+t航；t搜为同上，即搜索行动所需时间；S1为从发现目标潜艇至反潜机到达潜艇初始位置时间内目标潜艇最小扩散面积，S1=π(vmin⋅t总)2；S2为从发现目标潜艇至反潜机到达潜艇初始位置期间目标潜艇以v潜航行的扩散面积，S2=π(v潜⋅t总)2；S3为从发现目标潜艇至反潜机到达潜艇初始位置时间内目标潜艇最大扩散面积，S3=π(vmax⋅t总)2；S4为从发现目标潜艇至反潜机完成搜索任务时间内目标潜艇最大扩散面积，S4= π(v潜(t总+t搜）]2。

实际需要搜索的面积：

S实=S4-S1= π[v潜(t总+t搜）]2- π(vmin⋅t总)2

上述面积公式意义：无论潜艇航向如何，在反潜飞机到达初始位置时刻，目标潜艇出现在S1区域的概率为0。这里vmin的估计可借助风险偏好理论相关内容，在此不作论述。示意图如图2所示。

3.2 搜索区域潜艇位置的概率密度特征

搜索区域的确定只是从理论上圈定了目标潜艇可能存在的最大范围。要实施搜潜行动，提高搜潜效率，必须研究搜潜规律，增强搜潜针对性，为科学决策搜潜方案提供依据。如图2所示，潜艇位置用极坐标(r，θ)表示。

图2 优化的确定应召反潜搜索区示意图

3.2.1 极半径r和极角θ上潜艇的概率密度特征

以初始位置时刻对目标潜艇的判断航向（φ）为参考角度0，以逆时针转向为正值，顺时针转向为负值。则在t总+∆t时刻，目标潜艇偏离的相对角度θ服从正态分布，并且其概率密度函数f(θ)的图形关于直线 θ=0对称，如式（2）：

3.2.2 搜索区域内潜艇的概率密度特征

应该明确的是，目标潜艇在搜索区域内的存在位置由r和θ共同决定。上面已经对潜艇所在半径位置和偏离预测航向的正态分布特性进行了讨论，可以推知反潜飞机到达初始位置时刻目标潜艇在搜索区域内的存在状况服从以r和θ为变量的联合正态分布，潜艇在搜索区域内的联合概率密度函数如式（3）：

其中，r1≤r≤r3，-π≤θ≤+π。

一般在反潜机达到初始位置后，目标潜艇一直在沿着半径方向运动，随着时间的推移这种位置的变化必然会带来潜艇在搜索区域内的联合概率密度发生改变，这种变化我们应当加以考虑和计算。在t总+∆t时刻，潜艇在搜索区域内的联合概率密度函数见式（4）：

其中 r1+v潜⋅∆t≤r≤r3+v潜⋅∆t，-π≤θ≤+π ，v潜⋅∆t表示在∆t时间内潜艇在半径方向发生的位移。

参数σ1、σ2、ρ的确定有两种方法：一种方法是依据试验或实战积累的大量数据，借助数理统计理论分析得出，这个问题的求证超出笔者能力范围，在此不再讨论；在没有试验数据的情况下，另一种方法是进行风险决策［3］，主要的决策准则有乐观准则、悲观准则、折衷准则、遗憾准则和等可能性准则。图3为 ρ=0.1、μ1=0、μ2=0、σ1=2、σ2=3的二维正态分布图及其概率密度等值线图。

图3 二维正态分布概率密度图及其等值线图

3.2.3 搜索区域的进一步优化

由概率分布密度函数公式及仿真图形可知，在搜索区域内存在一个如图4所示粗线表示的椭圆区，椭圆中心点极坐标为 (r中，0)，r中=v潜⋅(t总+∆t)，短轴与-→----OB共线。该椭圆区是t总+∆t时刻目标潜艇存在的最大可能区域，潜艇出现在该区域某点(r，θ)的概率密度值与|r-r中|和 ||θ 均成反比关系。因此，该椭圆区是反潜飞机重点搜索区域，搜索时应按照潜艇出现在该区的概率密度大小合理设置搜索密度和探测设备投放密度。

4 搜索区域的优化对搜索行动的影响

4.1 搜索行动起始坐标的选择

搜索起始坐标的选择对于搜潜效率的提高起着至关重要的作用。要科学决策搜索起始坐标，必须从两个方面进行考虑：一是目标潜艇所在位置的半径；二是目标潜艇所在位置的相对角度。这两个方面的因素相互关联，共同决定着搜潜起始坐标［4～5］。

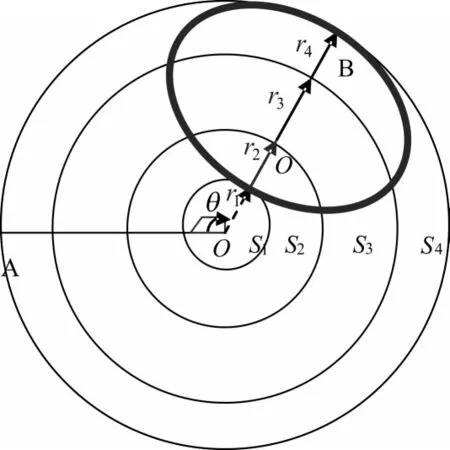
图4 反潜搜索中重点搜索区示意图

由图3中的联合正态分布概率密度等值线可知，最佳起始搜索位置应该选择在点(r，θ)=(r2，0)的邻域内。

4.2 搜索路径的拟合模型［6］

设反潜机搜索潜艇起点为O′，基于对目标潜艇存在的联合概率分布密度和潜艇向外扩散的考虑，搜索路径应该是一条自O′出发不断向外扩展的椭圆螺线，该螺线随着|r-r中|和角度 ||θ的增大步长逐渐增大。

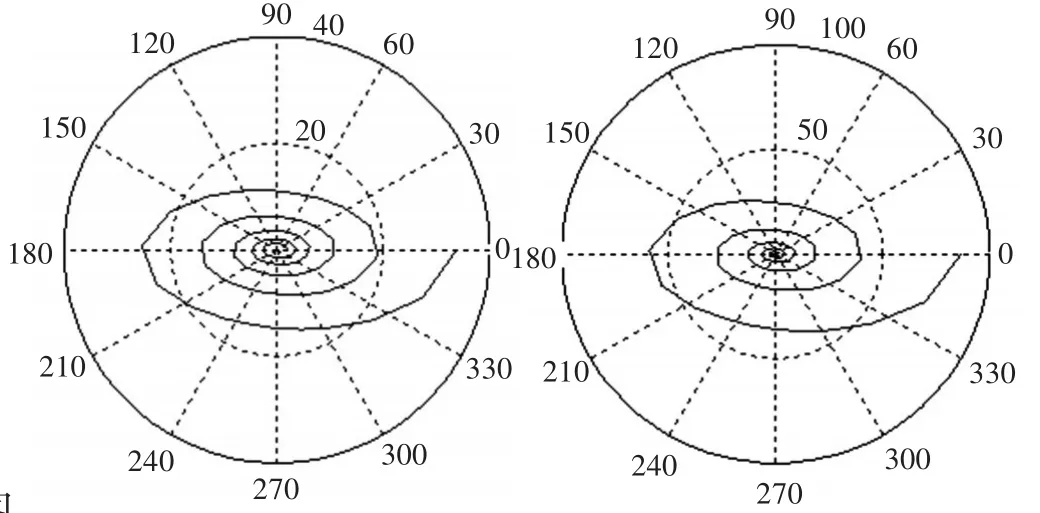
图5 搜索路径仿真图

该约束条件意味着潜艇在飞机飞行一圈所需时间内移动的距离应当小于或等于飞机在半径方向上移动的距离，一旦该条件不满足应该及时修正路径参数，从而保证搜索的可靠性。由此可知，在搜索过程中，飞机最佳搜索速度是当上式取等号时的飞行速度。

5 结语

优化潜艇搜索区域后，建立搜索路径的拟合模型，我们可以通过将典型战术技术参数带入公式，进行定量分析，以期对战术动作提供一定的指导。在航空反潜搜索行动中，对搜索区域的优化是提高搜潜效率的重要途径，很多具体细节还可以进一步从理论上优化，在试验中论证，希望本文的工作能起一个抛砖引玉的作用。

［1］孙明太.航空反潜概论［M］.北京：国防工业出版社，1998：344-345.

［2］谭乐祖等.最小二乘法在直升机扇形应召搜潜阵中的应用［J］.舰船电子工程，2016，36（1）：20-22.

［3］彭勇行.管理决策分析［M］.北京：科学出版社，2000.

［4］李长明.舰载直升机反潜搜索最佳方案优选模型及应用［J］.火力与指挥控制，2005，30（8）：68-71.

［5］战凯.对策论在航空反潜搜索效能评估中的应用研究［J］.系统仿真学报，2006，18（8）：2086-2088.

［6］谭乐祖，张诗等.直升机单机等距螺旋应召搜潜效能模型与仿真.火力与指挥控制，2016，41（8）：102-104.