改进的K-means融合微粒群优化的基因选择方法
杜洪波,白阿珍,朱立军
(1.沈阳工业大学 理学院,辽宁 沈阳 110870; 2.北方民族大学 信息与计算科学学院,宁夏 银川 750021)
微阵列数据的显著特点是样本小、基因的维数大、高噪声[1],并且存在基因选择难的问题。为了解决此问题,多种方法已经被运用来处理微阵列数据,譬如,聚类算法[2]、基因选择方法[3]、分类算法[4]。
聚类算法是研究基因之间的相互关系的最基本的手段[1]。聚类能够将功能相似的基因聚成一类,并且按照聚类的结果,预测未知的基因功能,寻找基因之间的调控关系和发现共同的模式[5]。由于基因芯片中含有大量的冗余的基因,对基因进行分类之前非常有必要对其进行去冗余工作,而基因选择方法就是一种合适的选择方法。
综上讨论,对基因微阵列运用改进的K-means融合PSO算法进行基因选择问题的研究。首先,运用过滤法Relief对基因进行筛选;然后,利用改进的K-means算法进行分类,并利用PSO寻优;最后,训练SVM,并评价获得的最优特征基因子集的质量。提出的 “改进的K-means算法融合微粒群优化算法”简称为“IK-PSO算法”。
1 相关算法
1.1 改进的DPC算法
DPC是2014年由Alex Rodriguez和Alessandro Laio提出来的一种基于密度的新的聚类算法[6]。DPC算法的思想是:聚类中心往往是由一些局部密度较低的数据对象所包围,并且与任何具有较高局部密度的其它的数据对象之间的距离都相对较大。
在DPC算法中,局部密度ρi和距离δi的计算依赖于截断距离dc,而DPC中的截断距离dc是通过人工设置的,属于人工经验的方法,虽然,截断距离dc的选择具有鲁棒性,但是,仍然缺少理论依据。因此,运用文献[7]中的选取截断距离的方法来对DPC进行改进。
对于数据对象i计算与其余各数据对象之间的赋权欧氏距离dij(i,j=1,2,…,n;i≠j),从而得到向量li={di1,di2,…,din},接着将li进行升序排序进而得到向量ci=sort(li)={ai1,ai2,…,ain},再将ci中的两两相邻的元素进行做差运算,并根据下列公式得到数据对象i的截断距离dci为
dci=aij|max(ai(j+1)-aij)
(1)
式中,max(ai(j+1)-aij)是向量ci中相邻的两个元素之差的最大值。
对于每一个数据对象i都有一个截断距离dci,因此,这些截断距离就可以构成一个集合Dc={dc1,dc2,…,dcn},而要选择的最优截断距离dc=min(Dc)。
这种改进的方法为截断距离dc的选择提供了依据,而且容易实现、算法简单。
1.2 K-means算法
K-means算法[8]是以K为参数,将数据集对象分成K个簇,使得簇内的相似度尽可能较高,而簇间的相似度尽可能较低,其相似度是根据数据对象与一个簇中所有对象的平均值(即聚类中心)之间的距离来进行度量的。
K-means的目标函数为
(2)
式中,E是数据集中的所有数据对象的平方误差总和;p是数据集中的数据对象;mi是类簇Ci的中心。
K-means算法描述如下:
输入:包含n个对象的数据集和簇的数目K。
输出:满足目标函数最小值的K个簇。
Step1:从n个数据对象中随机地选择K个对象作为初始聚类中心;
Step2:对剩余对象,根据它与聚类中心的距离,并根据最小距离原则将其指派到相应的类簇中进行划分;
Step3:计算每个类簇的新的均值,即新的类簇中心;
Step4:回到Step2,循环,直到聚类中心不再发生变化。
1.3 基于改进的DPC算法的K-means算法
针对K-means需要人为地确定聚类个数,随机地选择初始聚类中心进行迭代从而导致不稳定的聚类结果的缺陷,可以通过改进的DPC来自动确定聚类数目以及选取聚类中心作为K-means的初始聚类中心,接着运用K-means算法进行迭代。而在基于改进的DPC算法的K-means算法中改进的DPC是利用文献[7]中介绍的方法来选择最优截断距离dc。此外,利用赋权欧氏距离[9]来更准确地规范各对象的差异程度,从而更好地聚类。
改进的K-means算法具体描述:
输入:含有n个数据对象的数据集合。
输出:满足目标函数最小值的K个簇。
Step1:运用熵值法来计算各个数据对象之间的赋权欧氏距离dij,并令dij=dji,i Step2:确定截断距离dc; Step3:根据确定的截断距离dc,并利用DPC算法中的方法计算每个数据对象i的ρi和δi; Step4:根据γi=ρi×δi(i=1,2,…,n),γi的值越大,则i就越有可能是聚类的中心; Step5:确定聚类中心cj(j=1,2,…,K)与K的值; Step6:计算剩余每个数据对象与各类簇的中心的距离,并将每个数据对象分类给距其最近的类簇中,从而达到划分的目的; Step7:重新计算每个新簇的均值作为新的类簇中心; Step8:计算目标函数值; Step9:直到目标函数不再发生任何的变化,算法终止;否则,转Step7。 PSO算法[10](微粒群优化算法)的思想来源于对鸟群捕食行为的研究,它是模拟鸟集群飞行觅食的行为,鸟之间通过集体的协作从而使群体达到最优目的。PSO随机初始化粒子,并且粒子的速度根据它本身的飞行经验以及同伴的飞行经验进行动态的调整,而粒子的速度和位置按照以下的方程式进行迭代: vid=ωvid+c1r1(pid-xid)+c2r2(pgd-xgd) (3) xid=xid+vid (4) 式中,ω是惯性权重值;c1,c2为正常数,称为加速系数;r1,r2分别是[0,1]范围内变化的随机常数。 因为微阵列具有高维、小样本的特点,如果仅使用PSO算法随机地搜索最优特征基因子集,无疑则会增加搜索的难度,从而降低搜索能力。因此,提出IK-PSO来对基因进行选择。首先,对于数据集未划分成训练集和测试集的则利用bootstrap法将其划分成训练集和测试集;接着,在训练集上运用过滤法Relief对基因进行初步筛选,选择出对分类贡献大的基因从而构成备选基因子集;然后,利用改进的K-means聚类算法将基因划分成一定数量的簇,并运用PSO对每一类簇进行搜索选择出相应类簇中的最优基因构成最优特征基因子集,在选择基因时,只选择最优的基因可能会丢掉原本数据集中一些相对重要的基因,因此,除了要找出不同类簇中最优的基因外,相应的也要找到相对应类簇中的次重要的基因,从而构成最优特征基因子集;最后,针对前面选择的最优特征基因子集来训练SVM,并利用其分类的性能来评价得到的最优特征基因子集的质量。 IK-PSO算法具体步骤如下: Step1:利用bootstrap将微阵列数据划分成训练集与测试集; Step2:运用过滤法Relief对基因进行筛选,筛选出对分类贡献相对较大的基因构成备选基因子集; Step3:在训练集中,对在Step2中筛选出的备选基因运用改进的K-means算法进行聚类,从而,得到聚类数K和聚类分类; Step4:对于Step3产生的类簇中未进行PSO寻优的一类簇将其看作粒子群,则粒子群的长度由相应簇中的基因决定; Step5:将Step4中的粒子群进行速度和位置的初始化; Step6:计算每个粒子的适应度; Step7:根据适应度更新pbest和gbest; Step8:根据PSO更新每个粒子的位置、速度; Step9:如果达到最大的迭代次数则算法终止,否则转到Step5; Step10:如果Step9后算法终止,从得到的结果中选择最优基因和次优基因,并将其加入最优特征基因子集O中; Step11:若无类簇未进行PSO寻优,则算法终止,否则转到Step4; Step12:利用集合O训练分类器SVM,从而利用其分类的精确率来评价选择的最优特征基因的分类性能。 利用典型的、公开的小样本,高维微阵列数据集结肠癌数据集(Colon)和结肠癌数据集(Leukemia)来进行IK-PSO算法的测试。有关这两个微阵列数据集的信息如表1所示。 表1 两个微阵列数据集的相关信息 其中,Colon数据集最初是由Alon等分析的结肠癌数据集[11],其包含了62个样本的数据,22个正常的组织(positive)以及40个的肿瘤组织(negative),并且,每个样本的2 000个基因都是从其含有的6 500个基因中初选得来的。而Leukemia是由Golub等在1999年公布的急性白血病数据集[12],此数据集总共包括72个样本,而每个样本均含有7 129个基因的数据表达。并且,其中25个为急性骨髓性白血病(Acute Myeloid Leukemia,AML),47个为急性淋巴性白血病(Acute Lymphoblastic Leukemia,ALL)。在试验的过程中将这些样本随机地划分成34个测试集和38个训练集。 IK-PSO在数据Colon、Leukemia上的分类精确率如表2所示。 表2 IK-PSO的分类精确率 为了说明IK-PSO的适用性,将IK-PSO与F+SVMRFE、F+SVMDEA等算法进行了比较,所选择的基本都是以Filter为基础,进行基因预选的算法。比较结果如表3、图1所示。 表3 算法精确率的比较结果 图1 不同数据集不同算法的分类准确率对比 根据表3,可以看出在Colon中,IK-PSO除了相对于最大相关最小冗余算法的精确率稍有所提高外,而相对于其余的几种算法的分类精确率显著提高,而在Leukemia上,IK-PSO的分类精确率相较于R+PSO、最大相关最小冗余外,而相对于其余的三种算法均有所提高。综上所述,提出的IK-PSO算法能够有效地选择出数据集的最优特征基因子集,进而获得较高的分类精确率。 为了解决高维、小样本的基因数据集的基因选择困难的问题,提出IK-PSO来对基因进行选择,其结合了筛选、聚类以及PSO寻优的性能,并在两个经典的癌症数据集上进行了验证。实验结果表明,将本算法应用到基因微阵列的基因选择中能够选择出有效的基因子集进而提高分类的精确率。 [1] 杨善秀,韩 飞,关 健.基于聚类和微粒群优化的基因选择新方法[J].计算机应用,2013,05:1285-1288. [2] VARMA S,SIMON R.Iterative class discovery and feature selection using minimal spanning trees[J].BMC Bioinformatics,2004,5:126. [3] YAO F Z,COQUERY J,CAO K A L.Independent principal component analysis for biologically meaningful dimension reduction of large biological data sets [J].BMC Bioinformatics,2012,13(1):1-15. [4] 于化龙,顾国昌,刘海波,等.基于相关性分析的微阵列数据集成分类研究[J].计算机研究与发展,2010,02:328-335. [5] RANA S,JASOLA S,KUMAR R.A hybrid sequential approach for data clustering using K-means and particle swarm optimization algorithm[J].International Journal of Engineering,Science and Technology,2010,2(6):167-176. [6] RODRIGUEZ A,LAIO A.Rodriguez , A.Laio.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496. [7] 双翼帆,顾幸生.基于改进的快速搜索聚类算法和高斯过程回归的催化重整脱氯前氢气纯度多模型建模方法[J].化工报,2016,03:765-772. [8] 陈磊磊.不同距离测度的K-Means文本聚类研究[J].软件,2015,36(01):56-61. [9] 盛 华,张桂珠.一种融合K-means和快速密度峰值搜索算法的聚类方法[J].计算机应用与软件,2016,10:260-264,269. [10]杜洪波,董文娟.Relief-PSO混合算法在基因微阵列特征选择中的应用[J].沈阳工程学院学报:自然科学版,2016,12(03):267-271. [11]ALON U,BARKAI N,NOTTERMAN D A,et al.Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays[J].Proceedings of the National Academy of Sciences USA,1999,96(12):6745-6750. [12]GOLUB T R,SLONIM D K,TAMAYO P,et al.Molecular classification of cancer:Class discovery and class prediction by gene expression monitoring[J].Science,1999,286 (5439):531-536.1.4 PSO算法
2 IK-PSO算法
3 实验分析
3.1 实验数据

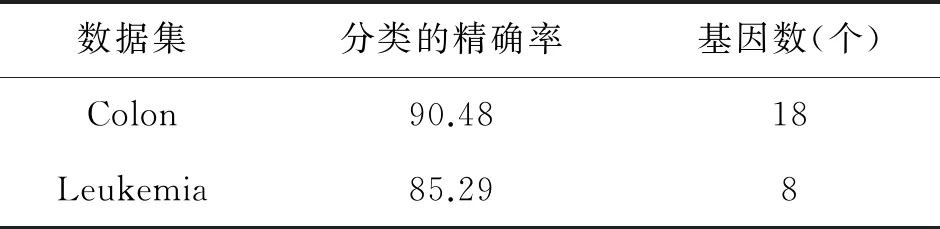
3.2 实验结果
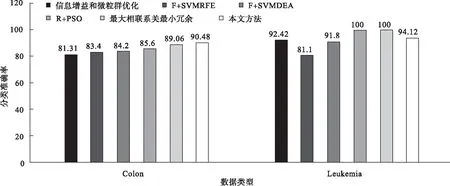
3.3 与F+SVMRFE、F+SVMDEA等算法的比较

4 结 语

