利用全信息声发射仪实现恢复系数与重力加速度的快速测量

李 辉 闫向宏 亓 鹏 赵 今

(中国石油大学(华东)理学院，山东 青岛 266580)

恢复系数和重力加速度是普通物理学中两个重要的物理参量。恢复系数反映了在碰撞过程中系统恢复形变的能力，也反映了碰撞过程中能量的损失情况，在许多学科中都有广泛的应用[1-4]。对于弹性碰撞的理论探讨[5-10]及恢复系数的测量方法[11-14]前人已作了大量的研究。重力加速度的测量常采用落球法或单摆法[15-17]。恢复系数和重力加速度这两个物理测量结果的精度都取决于微小时间间隔的测量精度，为此本文利用先进的DS2型全信息声发射信号分析仪构建了弹性碰撞恢复系数和重力加速度快速测量实验系统，利用声发射信号分析仪高速的数据采集和存储技术，实时记录碰撞过程的时域波形，为后续提取高质量的相邻两次碰撞时间间隔序列提供保障，从而实现对恢复系数和重力加速度的快速准确测量。对传统物理实验设备进行现代化、智能化升级[18-21]，实现物理实验的现代化也是大势所趋。

1 测量原理

设质量为m的小球从高度h处自静止开始自由下落，以速率V0与一静止且质量较大的水平面发生弹性碰撞，碰撞后小球上升速率为V1，根据普通物理学中有关一维弹性碰撞恢复系数定义，则有

(1)

式(1)中，g为重力加速度；h1为小球第一次与水平面碰撞后上升高度。令小球第一次与水平面碰撞时为计时起点，则第n次与水平面碰撞到第n+1次碰撞所需时间为

(2)

其中hn为小球第n次与水平面碰撞后上升高度，可由下式给出

(3)

则小球与水平面间碰撞的时间序列Tn满足

(4)

对式(4)两边取自然对数，可得

(5)

由式(5)可知，小球与水平面间碰撞次数n 与lnTn之间满足线性关系，由该直线的斜率与截距即可求得小球与水平面之间一维弹性碰撞的恢复系数e和重力加速度g。

2 实验测量装置

由DS2型全信息声发射信号分析仪组成的实验测量装置如图1所示，该全信息声发射信号分析仪，是以记录波形为主，同步产生声发射参数，在声发射研究领域有重要应用。将声波传感器利用磁力座固定在作为碰撞水平面的钢板上，小球与钢板碰撞时产生的冲击力会激发声波传感器产生电信号，经过SmartAE前置放大器处理后，利用全信息声发射信号分析仪自带波形采集程序控制16位高速A/D转换卡完成碰撞波形的实时采集、显示，由实时记录的碰撞波形即可准确求出相邻两次碰撞之间的时间间隔，精度可达μs量级。

图1 实验装置示意图

3 实验结果及分析

实验中选取了小钢球(φ7.88mm、m=2.0g)与瓷砖地面、玻璃球(φ13.98mm、m=3.51g)与钢板及弹力球(φ 33.31mm、m=26.5g)与钢板之间3种不同的碰撞模式进行实验测试。在小钢球与瓷砖地面发生碰撞时，小钢球给予瓷砖地面的碰撞冲击力通过声学换能器转化为电压信号输出，经前置放大及高速数据采集后可得如图2所示的多次弹性碰撞时域波形，对某次碰撞波形经放大后显示于图2右上角，t0为从高度h由静止下落到碰撞水平面所需的时间。每次碰撞波形上第一个过零点的位置称为波至点，相邻两次碰撞的波至点之间的时间差即为碰撞时间间隔Tn。对多次弹性碰撞的波形序列进行处理，可分别获得小钢球—瓷砖地面、玻璃球—钢板及弹力球—钢板之间的碰撞时间间隔Tn及lnTn如表1至表3所示。

表1 小刚球—瓷砖地面间弹性碰撞恢复系数及重力加速度计算结果(h=478mm)

表2 玻璃球—钢板间弹性碰撞恢复系数计算结果(h=497mm)

表3 弹力球—钢板间弹性碰撞恢复系数计算结果(h=750mm)

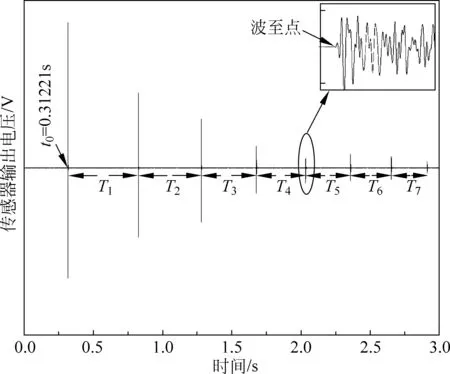
图2 小钢球与瓷砖地面间弹性碰撞的时域波形

利用表1至表3中数据绘制出小钢球—瓷砖地面、玻璃球—钢板及弹力球—钢板之间碰撞的lnTn与碰撞次数n的关系曲线如图3至图5所示。

由图3至图5的曲线可知，小钢球—瓷砖地面间、玻璃球—钢板间以及弹力球—钢板间的碰撞，lnTn-n都满足线性规律。经线性拟合后分别得到3种不同碰撞模式所满足的线性方程分别为

小钢球—瓷砖地面间： lnTn=-0.46999-0.11653·n

玻璃球—钢板间： lnTn=-0.45072-0.17918·n

弹力球—钢板间： lnTn=-0.24394-0.15842·n

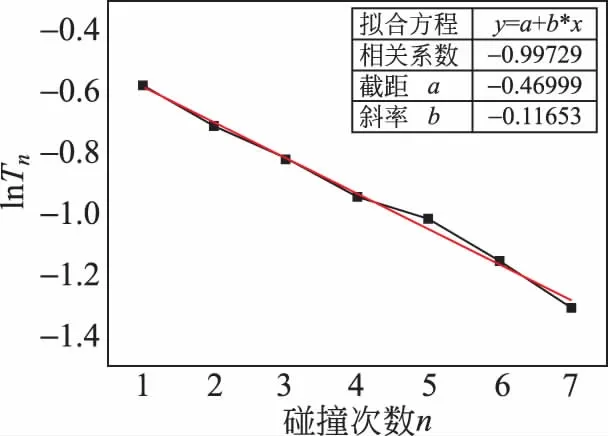
图3 小钢球—瓷砖地面间弹性碰撞lnTn-n曲线

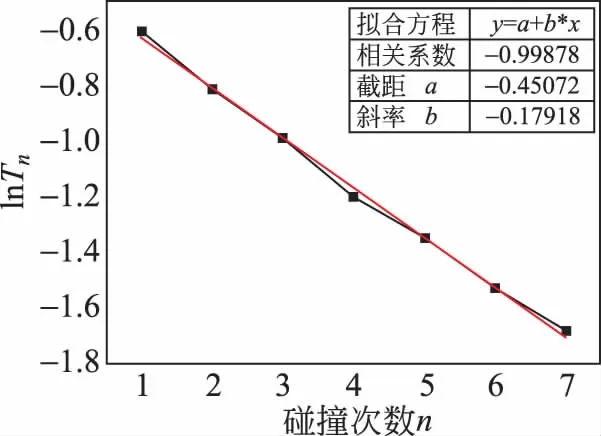
图4 玻璃球—钢板间弹性碰撞lnTn-n曲线

图5 弹力球—钢板间弹性碰撞lnTn-n曲线

由3种碰撞模式的线性方程的斜率及截距分别求出小钢球—瓷砖地面间弹性碰撞的恢复系数为0.8901，玻璃球—钢板间弹性碰撞的恢复系数为0.8360，弹力球—钢板间弹性碰撞恢复系数为0.8535，按文献[12、14]的方法计算出的弹性碰撞恢复系数的误差在2%以内。由3种碰撞模式计算出的重力加速度分别为9.789m·s-2、9.793m·s-2和9.773m·s-2，重力加速度的平均值为9.785m·s-2，与按照黄岛地区纬度计算出的重力加速度值9.798m·s-2非常接近。

本文采用DS2型全信息声发射信号分析仪构建的一维弹性碰撞恢复系数及重力加速度测量系统，利用高速数据采集技术捕捉弹性碰撞瞬间的时域波形，记录的波形清晰、完整，提高了相邻两次碰撞之间时间间隔的测量精度，实验原理简洁明了，实验测量的精度和稳定性较高。恢复系数的测量误差主要来源于小球是否垂直入射碰撞平面，如果小球不是垂直入射碰撞平面，则实验测量结果仅反映垂直方向上的恢复系数，而对于水平方向的恢复系数目前还不便测量。

4 结论

(1) 本文利用全信息声发射信号分析仪实时记录小球与平板之间碰撞信号的时域波形，从实现对弹性碰撞恢复系数和重力加速度的快速测量，具有实验原理简单清晰、记录的碰撞波形清晰完整、实验测量便捷、快速、实验测量结果准确、可靠的特点。

(2) 将先进的声发射设备应用到普通物理学中重要的两个物理量——碰撞恢复系数及重力加速度的测量，培养学生利用现代科技改进传统的实验测量方法与技术，从而达到培养学生的创新意识和创新能力的目标。

[1] 何思明, 吴永, 李新坡. 滚石冲击碰撞恢复系数研究[J]. 岩土力学, 2009(03):623-627. HE Siming, WU Yong, LI Xinpo. Research on restitution coefficient of rock fall[J]. Rock and Soil Mechanics, 2009(03): 623-627. (in Chinese)

[2] 郑建祥, 刘洪雷. 弹性恢复系数对超细颗粒气固流场影响的研究[J]. 东北电力大学学报, 2010(06):10-14. ZHENG Jianxiang, LIU Honglei. Investigations on effect of the restitution coefficient of particle elasticity on gas and solid flow behavior of fine particle agglomerations in fluidized beds[J]. Journal Of Northeast Dianli University, 2010(06): 10-14. (in Chinese)

[3] 章广成, 向欣, 唐辉明. 落石碰撞恢复系数的现场试验与数值计算[J]. 岩石力学与工程学报, 2011(06):1266-1273. ZHANG Guangcheng, XIANG Xin, TANG Huiming. Field test and numerical calculation of restitution coefficient of rockfall collision[J]. Chinese Journal of Rock Mechanics and Engineering, 2011(06): 1266-1273. (in Chinese)

[4] 陆永光, 吴努, 王冰, 等. 花生荚果碰撞模型中恢复系数的测定及分析[J]. 中国农业大学学报, 2016(08):111-118. LU Yongguang, WU Nu, WANG Bin, et al. Measurement and analysis of peanuts’ restitution coefficient in point-to-plate collision mode[J]. Journal of China Agricultural University, 2016(08): 111-118. (in Chinese)

[5] 康垂令. 关于恢复系数e的讨论[J]. 大学物理, 1997(12): 19-21. KANG Chuiling. A Discussion on coefficient of restitutione[J]. College Physics, 1997(12): 19-21. (in Chinese)

[6] 覃铭. 力学碰撞中恢复系数的一般表达式[J]. 广西物理, 2004(02): 32-35. QIN Ming. General expression of recovery coefficient in mechanical collision[J]. Guangxi Wuli, 2004(02): 32-35. (in Chinese)

[7] 张九铸. 一般运动刚体的恢复系数公式的适用条件[J]. 力学与实践, 2010(03):116-117. ZHANG Jiuzhu. Applicable conditions for the coefficient formula of normal motion rigid body[J]. Mechanics and practice, 2010(03): 116-117. (in Chinese)

[8] 王悦. 一维对心碰撞恢复系数的讨论[J]. 物理与工程, 2014(05):66-69. WANG Yue. Discussion on the coefficient of restitution of one-dimension central collision[J]. Physics and Engineering, 2014(05): 66-69. (in Chinese)

[9] 姚文莉, 岳嵘. 有争议的碰撞恢复系数研究进展[J]. 振动与冲击, 2015(19):43-48. YAO Wenli, YUE Rong. Advance in controversial restitution coefficient study for impact problems[J]. Journal of vibration and shock, 2015(19): 43-48. (in Chinese)

[10] 李逸良, 邱信明, 张雄. 恢复系数的不同定义及其适用性分析[J]. 力学与实践, 2015(06):773-777. LI Yiliang, QIU Xinming, ZHANG Xiong. Different definitions and corresponding applicabilities of the coefficient of restitution[J]. Mechanics in Engineering, 2015(06): 773-777. (in Chinese)

[11] 吕茂烈. 碰撞恢复系数及其测定[J]. 固体力学学报, 1984(03):318-329. LV Maolie. Coefficients of restitution and their measurement[J]. Acta Mechanica Solida Sinica, 1984(03):318-329. (in Chinese)

[12] 耿宏章, 张卫强, 周开学. 恢复系数的测量[J]. 物理实验, 2003(01):39-41. GENG Hongzhang, ZHANG Weiqiang, ZHOU Kaixue. Measurement of restitution coefficient[J]. Applied Physics, 2003(01): 39-41. (in Chinese)

[13] 单信海, 任敦登. 足球弹性恢复系数的实验测定[J]. 浙江体育科学, 2006(04):90-92. SHAN Xinhai, REN Dundeng. Experiment determination of football COR[J]. Zhejiang Sport Science, 2006(04): 90-92. (in Chinese)

[14] 俞晓明, 崔益和, 陈飞, 等. 恢复系数及重力加速度的落球弹跳法测量[J]. 大学物理, 2010(11):35-36. YU Xiaoming, CUI Yihe, CHEN Fei, et al. Measurement of coefficient of restitution and gravitational acceleration by using bouncing ball[J]. College Physics, 2010(11): 35-36. (in Chinese)

[15] 朱道云, 庞玮, 吴肖, 等. 多管落球法测量重力加速度

[J]. 实验技术与管理, 2012(04):59-61. ZHU Daoyun, PANG Wei, WU Xiao, et al. Measuring acceleration of gravity by multi-tube falling-ball method[J]. Experimental Technology and Management, 2012(04): 59-61. (in Chinese)

[16] 尹学爱, 刘妮. 智能化单摆测重力加速度实验仪[J]. 实验科学与技术, 2016(06):82-84. YIN Xueai, LIU Ni. Intelligent simple pendulum experimental instrument of measuring acceleration of gravity[J]. Experiment Science and Technology, 2016(06): 82-84. (in Chinese)

[17] 龚云梅, 严霞, 李艳茹, 等. 落球法测定重力加速度的新方法[J]. 物理通报, 2016(09):101-102. GONG Yunmei, YAN Xia, LI Yanru, et al. A new method of measure acceleration of gravity by free-fall[J]. Physics Bulletin, 2016(09): 101-102. (in Chinese)

[18] 奚悦.高精度悬滴法液体表面张力实验系统研制[J].实验技术与管理,2015,32(6):69-71. XI Yue. Development of system with axisymmetric drop shape method for surface tension measurement[J]. Experimental Technology and Management, 2015,32(6): 69-71. (in Chinese)

[19] 郭启凯,郭敏强,李超,等.超声相位差法测量杨氏模量[J].实验技术与管理,2013,30(2):41-43. GUO Qikai, GUO Minqiang, LI Chao, et al. Young’s modulus measurement based on ultrasonic phase-difference method[J]. Experimental Technology and Management, 2013, 30(2): 41-43. (in Chinese)

[20] 陈诚,李香莲,刘伟伟,等.基于线阵CCD的智能化金属丝弹性模量测量仪设计[J].实验技术与管理,2016,33(1):104-106. CHEN Cheng, LI Xianglian, LIU Weiwei，et al. Design of measuring elasticity modulus instrument of wire by using linear CCD[J]. Experimental Technology and Management, 2016, 33(1): 104-106. (in Chinese)

[21] 陈卫红,邓晓刚.适合实践教学的新型温控系统设计[J].实验技术与管理,2015,32(11):94-98. CHEN Weihong, DENG Xiaogang. A new design of temperature control system for practical teaching[J]. Experimental Technology and Management, 2015, 32(11): 94-98. (in Chinese)