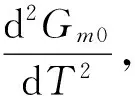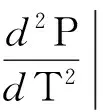朗道序参量理论计算液气流体系统的临界指数

岑理相

(四川大学物理科学与技术学院，四川 成都 610065)

朗道序参量理论[1]是研究连续相变的唯象理论。对于顺磁铁磁相变，朗道理论中的序参量由自发磁化M表征。由于系统自由能是M的偶函数，相变临界点对应自由能函数具单极小或双极小的分叉点。在临界点邻域将自由能以M的偶次幂作近似展开，依据实际系统中自由能函数取极小这一事实，可以得到系统序参量的具体表达。进一步，朗道理论还可以根据所得的自由能表达式计算系统的临界指数[1]。对于液气流体系统的临界点相变，临界温度以下液、气两相类比于磁矩取向相反的两种铁磁相，故而可以自然地引入气、液两相的比体积或密度之差作为系统的序参量。然而应用朗道理论进一步计算液气流体系统的临界指数会出现一个棘手的问题：不同于铁磁相对于变换M→-M是对称的，临界点以下液气系统的热力学势函数对于液、气两相并不对称。根据我们调研，现有教科书中往往只是定性解释气液流体系统临界点相变可与顺磁铁磁相变作类比[2-4]，但对于如何克服上述问题并实施具体计算鲜有教材和文献讨论。本文根据液气两相平衡共存时两相的化学势相等，提出可以利用系统吉布斯函数研究系统沿两相共存曲线趋于临界点的行为，从而给出应用朗道理论计算该体系临界指数的具体实现。

按照朗道理论的基本思想，我们引入Gm(T,P,ψ)描述系统在临界点邻域的摩尔吉布斯函数，其中T、P代表温度与压强两独立状态参量，ψ=v1-v2为序参量表征可能出现的两相摩尔体积之差。在临界点以下，气、液两相的热力学函数一般而言并不对称。但是我们可以考虑两相平衡共存情形：共存线上气、液化学势相同，因而有统一的吉布斯函数表达式。共存线上T、P仅有一个独立，即P=P(T)，故而可取Gm=Gm(T,P(T),ψ)。将吉布斯函数按ψ的幂展开

(1)

展开式中不出现奇次幂是因为两相共存曲线上吉布斯函数在ψ→-ψ变换下对称。

对于T、P一定系统，吉布斯函数取极小，故有

结合式(2a)、(2b)可以求得

ψ=0,a>0

(3a)

或

(3b)

解式(3a)对应临界点以上系统，即气、液不分状态，其吉布斯函数由Gm0(T,P)描述。解式(3b)对应临界点以下有序系统，可将正根视为气相，表示该相比体积大于与其共存的另一相; 负根视为液相，表示其比体积小于共存另一相。由于根为实数，故b>0。结合式(3a)、式(3b)可知在临界点处应有a=0。从而临界点邻域可简单假设b为正常数以及a的一般形式为

a(T,P)=aTt+aPp

(4)

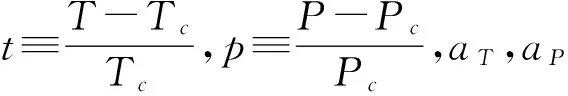
a(T,P)=aTt+aPp=(aT+kCaP)t

(5)

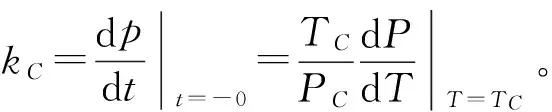
(6)

将以上所得的序参量表达式(6)代入式(1)，可得有序相在液、气平衡时的吉布斯函数

(7)

其中Gm0(T,P)也描述了临界点上方(T>TC一侧)无序相的吉布斯函数。为了比较临界点两侧系统的特性，我们不妨将两相平衡相图曲线P=P(T)延拓至无序相这一侧，以便考察临界点两侧系统吉布斯函数的方向导数以及相应热力学量的行为。首先观察吉布斯函数一阶导数

(8)

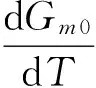
对式(8)进一步求导得T

(9)

(10)

(11)

以及

(12)

(13)

(14)

这说明两侧的定容比热是有限的，因此临界指数α=α′=0。这与磁性系统朗道理论的结果一致。

方程式(13)、(14)给出的气相和无序相的定容比热之差与液相和无序相之差在趋于临界点时两者一致，这也就表明了T→TC时气、液两相定容比热相同。这一结果也可以通过直接比较临界点下方气、液两相的定容比热得到。根据式(11)，我们有

(15)

代入序参量式(6)，即表明当T→TC(即t→-0)时两者之差将按照以下幂律趋于零

(16)

本文考察了两相平衡相图曲线上系统吉布斯函数表达，在此基础上应用朗道理论获得了两个临界指数：β=1/2与α=α′=0。这些结果与朗道理论处理磁性系统得到的临界指数一致。需要指出的是，论文对系统吉布斯函数的表达是不完备的：虽然能够对沿相图曲线的方向导数做出计算和分析，但有序相一侧吉布斯函数的一阶、二阶偏导表达式尚不能有效获取。相应地，描述等温压缩系数与压强临界行为的两个临界指数(一般由γ、δ表征)没有给出。这两个临界指数文献[5]曾通过范氏气体方程做过讨论(亦可参考[4,6])，本文不再赘述。

[1] LANDAU LD, Phys.[M]. Zeit. Sowjetunion 1937: 11, 26.

[2] 汪志诚. 热力学.统计物理[M]. 北京：高等教育出版社，2013: 99-105.

[3] 郝柏林,于渌,孙鑫,等. 统计物理学进展[M]. 北京：科学出版社，1981: 77-82.

[4] 林宗涵. 热力学与统计物理[M]. 北京：北京大学出版社，2007: 178-184.

[5] 朗道·栗弗席兹. 统计物理学[M]. 束仁贵,束莼，译. 北京：高等教育出版社，2011: 435-438.

[6] 于渌,郝柏林,陈晓松. 相变和临界现象[M]. 北京：科学出版社，2005: 76-81.