基于霍尔效应测量电磁辐射的研究

张沈麒 高 红 李 华 王 玫

(北京航空航天大学 1电子信息工程学院， 2物理科学与核能工程学院， 北京 100191)

家用电器和移动通信设备得到了广泛普及。一方面，人们生活的便利性得到大幅提升，另一方面，电磁辐射污染日益严重。现代文明离不开电，电能产生磁场，磁场则会向外辐射电磁波。各种研究证实，超过一定强度的电磁辐射污染会对我们的生产、生活乃至身体健康带来不同程度的不良影响[1]。因此，研究电磁辐射检测的原理，设计出高质量的电磁辐射检测仪不仅有利于检测环境的辐射，也有利于保护我们的身体健康。

测量电磁辐射强度的方法，主要分为测量电场强度，测量磁场强度和测量功率密度3大类[2]。本实验通过测量微弱的交变磁场强度来反映电磁辐射的大小。我们利用霍尔元件检测磁场强度，其具有功耗低，输出电阻小，测量准确，工作稳定的特点[3]。

1 实验原理简述

1.1 霍尔效应法测电磁辐射原理

霍尔效应法是一种常用的测量磁场强度的方法。霍尔元件产生的电动势称为霍尔电动势，其公式为

(1)

其中RHII为理论输出电压和待测磁场值之间的比例系数。

霍尔元件测量磁场的优点在于理论上输出电压仅和空间磁场总强度有关，而与频率无关。并且霍尔元器件十分灵敏，霍尔电场的建立仅需10-12s。但是由于一般RHII极小，故输出电压需要进行多级放大。

在实验中，采用AH49E线性霍尔传感器，这是一种十分灵敏的霍尔元器件，灵敏度为1.5mV/Gs。其输出值在-1000Gs到1000Gs范围内呈线性关系。并且其在正常工作温度区域内几乎不受温度影响。其结构图如图1所示。

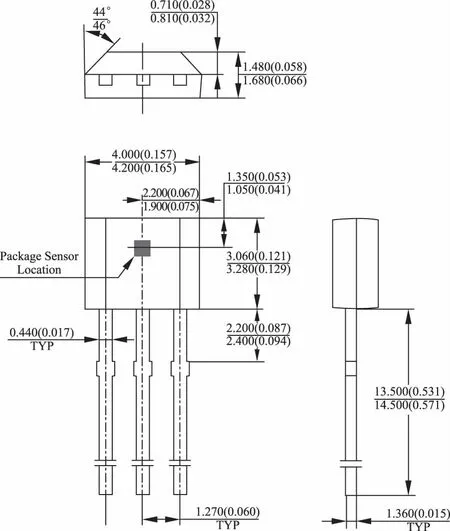
图1 AH49E线性霍尔传感器的结构图

霍尔传感器有3个引脚，分别为输入端，输出端和接地端。在输入端我们需要输入2.5V电压来让霍尔传感器工作在线性区。

1.2 磁场产生方法

本次实验中，我们通过亥姆霍兹线圈来产生磁场。亥姆霍兹线圈具有良好的磁场发生性能，在两线圈中点附近的磁场可以近似认为是匀强磁场，且方向与线圈轴线方向一致。本次实验中采用的亥姆霍兹线圈参数为

亥姆霍兹线圈产生的磁感应强度用公式

(2)

求得。其中，μ0为真空磁导率；N为线圈匝数；I为通过线圈的电流大小。由此可以算出磁场的理论值。

2 测量结果及数据分析

2.1 霍尔元件法测静磁场

为得到霍尔元件输出电压在输入电压一定的情况下与作用于元件表面的磁感应强度之间的关系，实验者向亥姆霍兹线圈通入直流电，从而产生静磁场，并利用AH49E线性霍尔传感器进行测量，实验中使磁场垂直作用有霍尔元件正表面。实验数据如表1和图2所示：

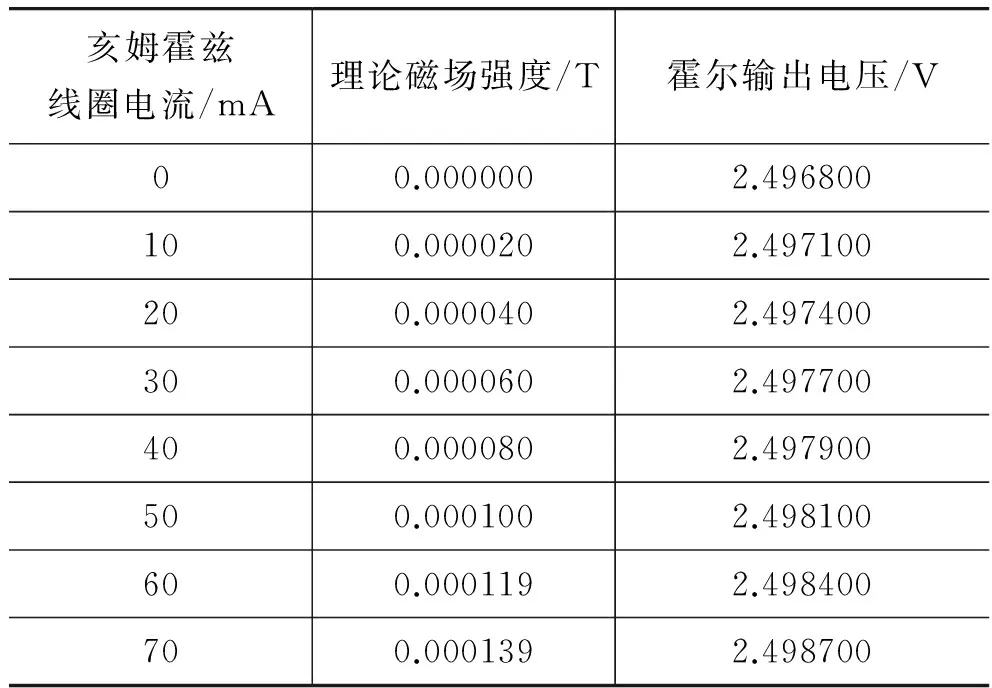
表1 霍尔元件测量静磁场强度

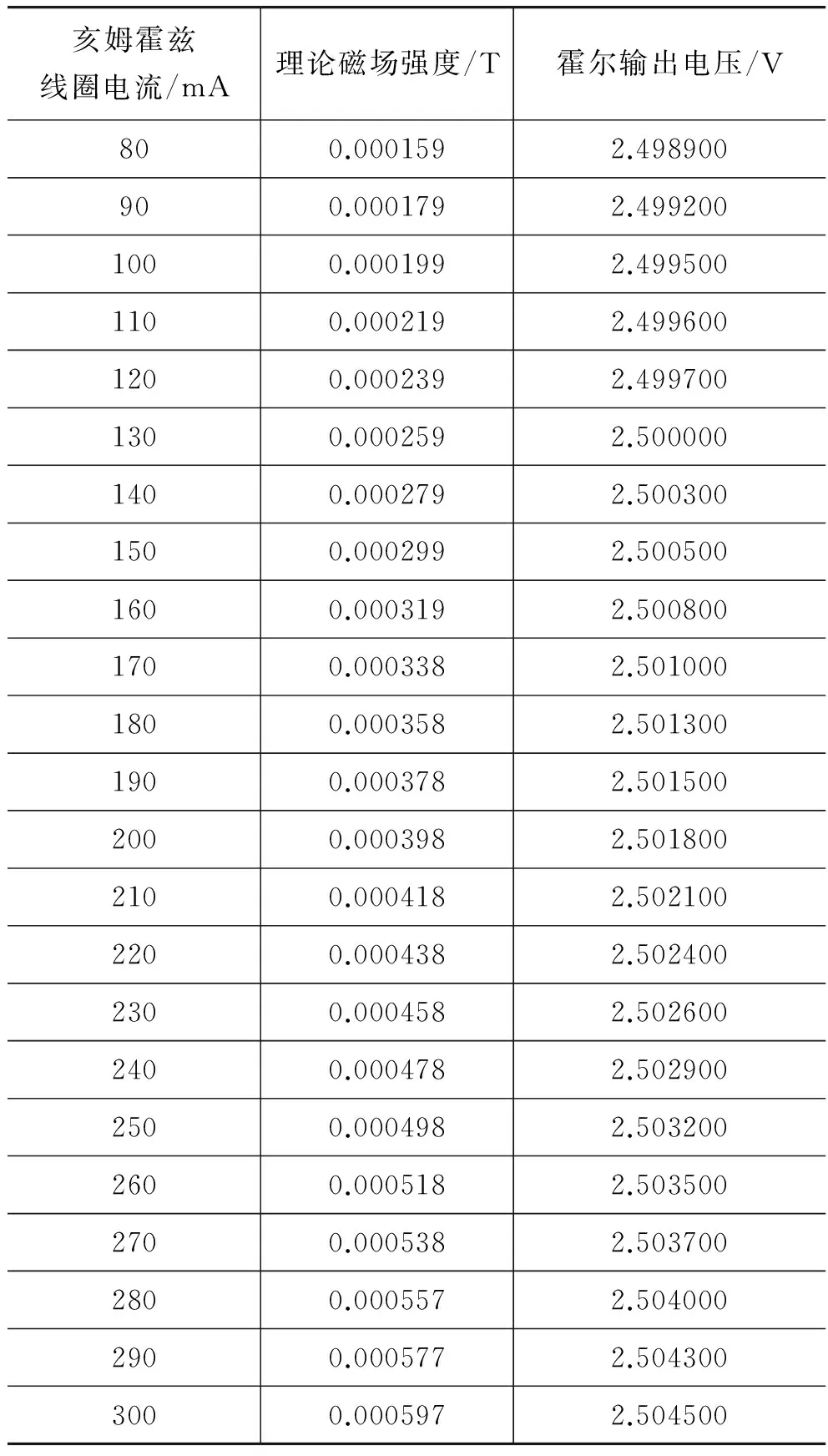
续表

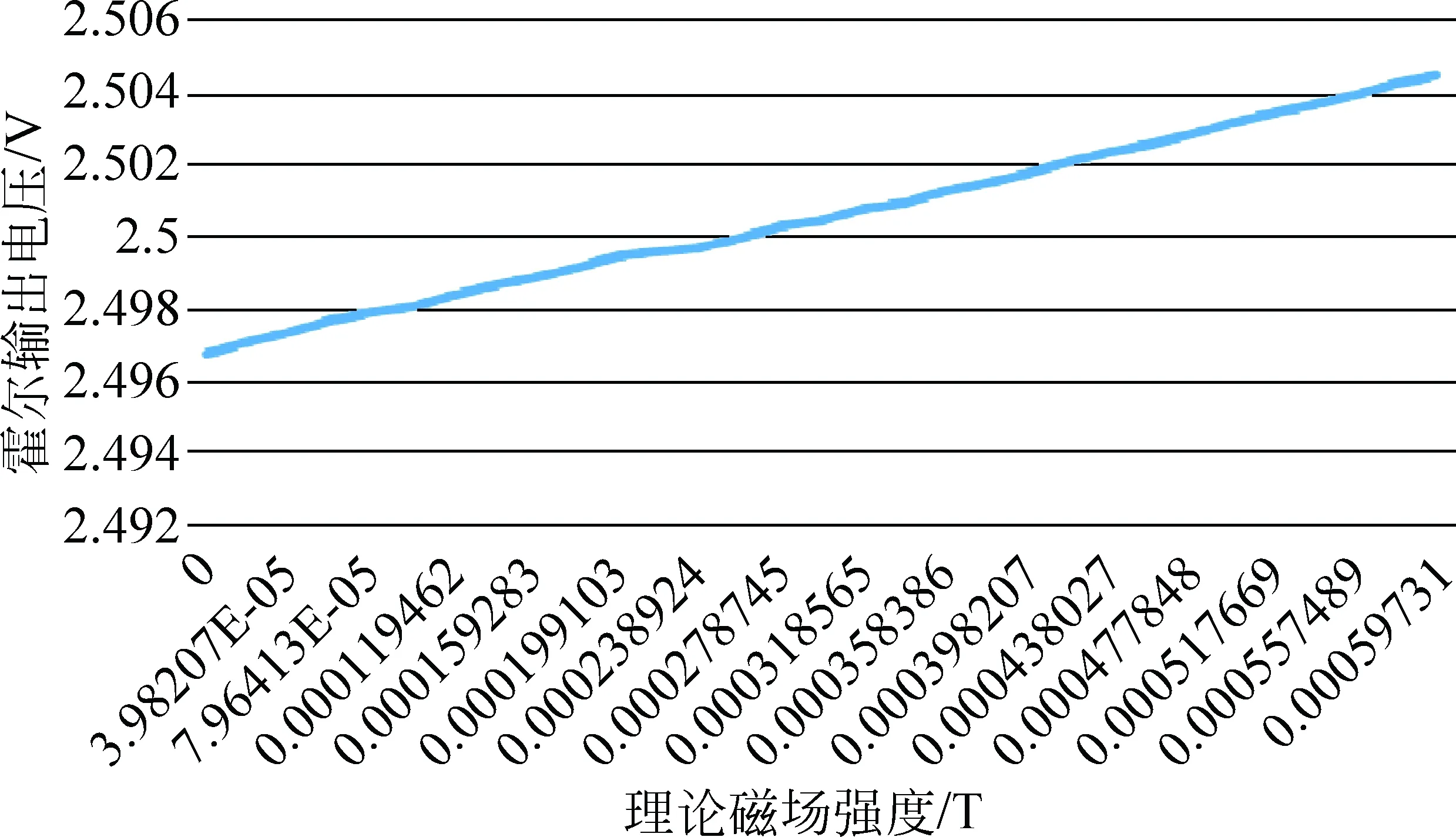
图2 霍尔元件输出电压与理论磁场强度的关系

经过线性回归，我们得到表征线性度的R值为0.999，可见线性度非常良好。线性霍尔元件的灵敏度系数为12.692V/T，即1.2692mV/Gs，和产品参数中的1.1～1.5mV/Gs的参数范围非常符合。静态输出值为2.497V，约为输入值5V的一半，符合产品参数。由此得到输出电压公式为

(3)

本组实验之外，实验者还进行了另一组实验，即在平行霍尔元件正表面的方向加载磁场。在此加载方案下发现霍尔元件的输出电压对磁感应强度的大小几乎没有响应。这一特性可以证明此型霍尔传感器具有极好的方向性。这是在制作各向同性探头时的理论依据。

2.2 霍尔元件法测交变磁场

在进行了霍尔传感器灵敏度验证之后，我们进行了用霍尔传感器测量交变磁场强度的实验。利用亥姆霍兹线圈通弱正弦交变电流产生较弱的交变磁场。弱正弦交变电流由函数信号发生器提供。本次实验中所加载的交变磁场均为1000Hz。

实验结果显示，霍尔元件输出电压的有效值与交变磁场的有效值线性关系良好，如表2 和图3所示。

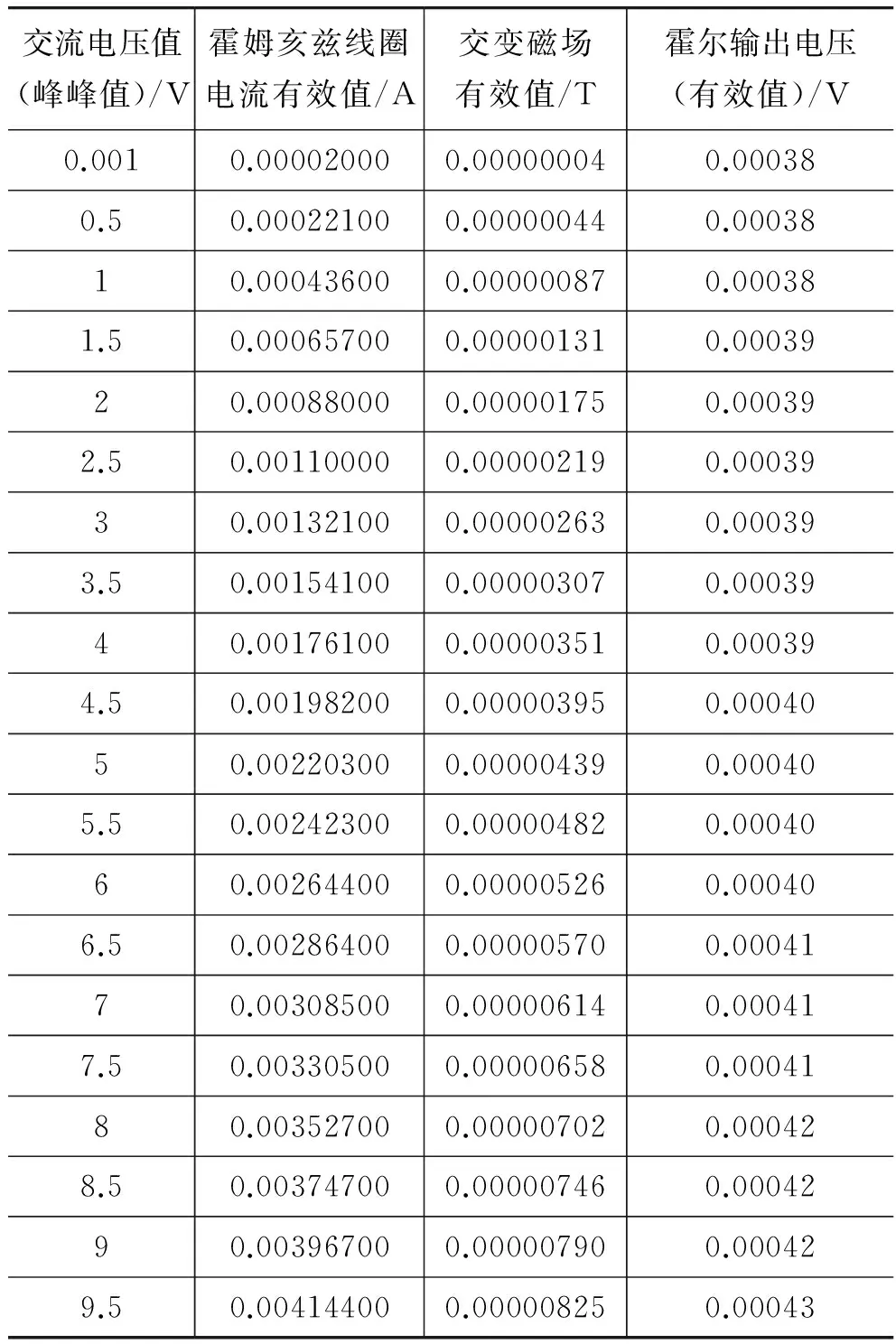
表2 霍尔元件测量1000Hz交变磁场

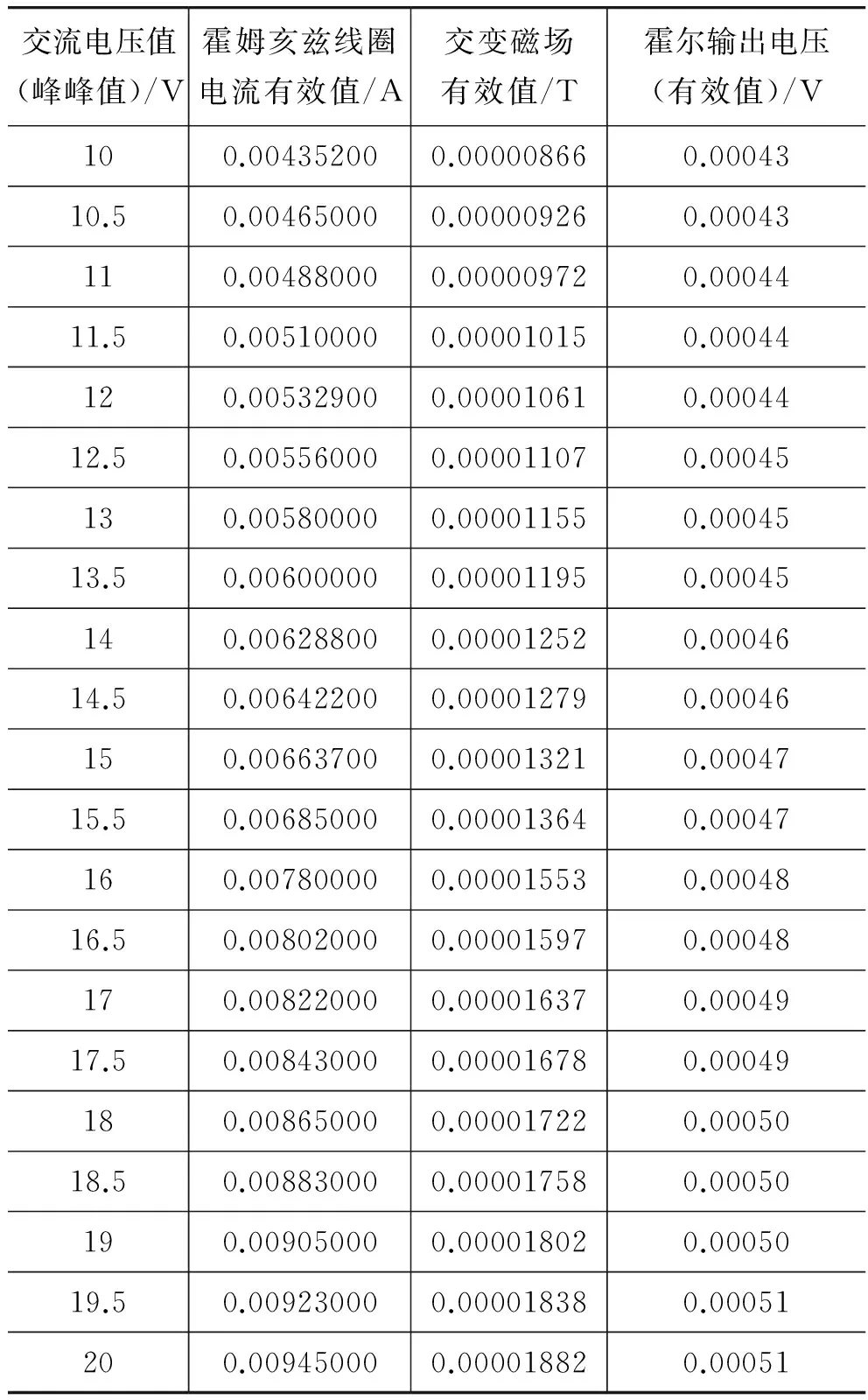
续表

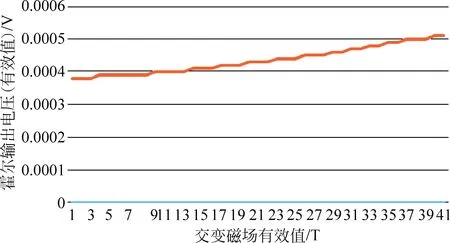
图3 霍尔元件输出电压有效值与理论交变磁场强度有效值的关系

经过线性回归，得到R值为0.993。在测量交变磁场时，霍尔元件的灵敏度为7.873V/T，这显然与加载静磁场时的灵敏度存在较大的差距。这是由于交变磁场在霍尔元件的电路上产生了一定的感生电动势。由此可以得到在加载交变磁场时的霍尔传感器电压输出公式为

(4)

(小写表示为交变量)

如果仅考虑交流值的有效值，则可得到公式为

(5)

(大写表示有效值)

其中，K为在测量静磁场时霍尔元件的灵敏度系数;K′是与感生电动势相关的系数，需要根据实验来测得。在测量1000Hz交变磁场时，霍尔元件的灵敏度为12.692V/T。

为验证霍尔输出电压和交变磁场频率之间的关系，我们进行了一组实验，即维持交变磁场强度一定(通过保持加载在亥姆霍兹线圈上的交变电流一定来实现)，改变其频率，得到测量数据如表3和图4所示。

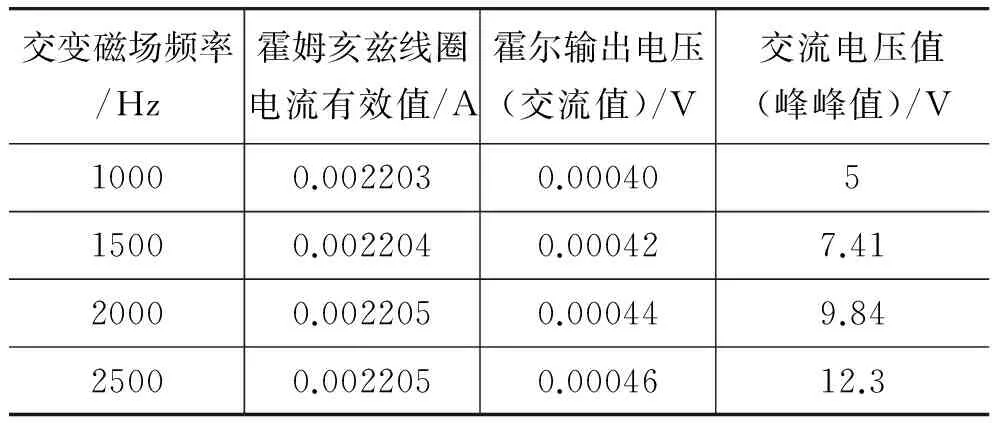
表3 霍尔元件测量不同频率的交变磁场

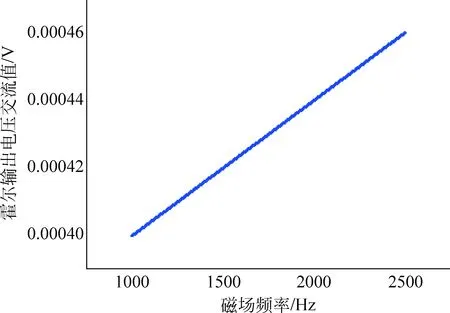
图4 霍尔输出电压有效值和磁场频率的关系

理论上霍尔元件输出电压与频率没有关系。实验结果表明，随频率变化，霍尔输出电压的有效值变化不明显，但是随着频率升高而变大。经过线性回归，R为1。

根据分析，这可能是由于元件线路上产生了感生电动势或者是内置放大元件对磁场产生了频率响应导致的[4]。也就是说，与感生电动势有关的系数K′并不是一个常数，在测量不同频率的磁场时，K′会有一定变化。为了减弱这一影响因素，我们需要进一步优化实验电路结构。

2.3 全向探头的制作与检测

实验者将3个霍尔元件固定在正交位置，组成了一个全向探头。为了验证全向探头的性能，实验者进行了以下实验。将霍尔元件全向探头与磁场方向呈一定角度放置，这样，记3个探头与磁场方向之间的夹角分别为α，β和γ，将3个方向上的霍尔元件的输出电压进行合成，可以得到总的输出电压。当加载静磁场时，实验结果如图5所示。

图5 全向探头对静磁场的测量图

实验结果很好地符合了预期。由此可以得到，当加载静磁场时，总的输出电压为

(6)

接着，用全向探头测量了交变电场，实验结果如图6所示。

实验结果同样很好地符合了预期。由此可以得到当加载交变磁场时，公式为：

(7)

若仅考虑交流值的有效值，则公式为

图6 全向探头对交变磁场的测量值

(8)

3 结语

本次实验中采用霍尔元件进行了磁场强度的测量，并制作了全向探头，取得了很好的效果。利用这一原理，我们可以制作电磁辐射检测探头，对电磁辐射进行防范。

[1] 陈杰, 梁四洋, 刘冰. 便携式电磁辐射测量仪的设计[J]. 电子测量技术, 2009(6): 58-60.CHENJie,LIANGSiyang,LIUBing.Thedesignofportableelectromagneticradiationdetectors[J].ElectronicMeasurementTechnology, 2009(6): 58-60. (inChinese)

[2] 殷春浩, 崔亦飞. 电磁测量原理及应用[M]. 北京：中国矿业大学出版社, 2008: 1-12.

[3] 杜义林. 霍尔集成电路在测量磁场中的应用[J]. 物理实验, 1994(5): 141-142.DUYilin.TheapplicationsofHallintegratedcircuitsinmeasuringmagneticfield[J].PhysicsExperimentation, 1994(5): 141-142. (inChinese)

[4] 郭宏福, 马超, 邓敬亚, 等. 电波测量原理与实验[M]. 西安：西安电子科技大学出版社, 2015: 214-216.