基于Buckley-Leverett理论的典型缝洞油藏一维驱替开发指标计算方法

吕爱民，王立伟，龙 涛，王传睿，董云振，赵健男，李绪延

(1.中国石油大学(华东) 石油工程学院，山东 青岛 266580;2.中石化 青岛安全工程研究院，山东 青岛 266000)

引 言

碳酸盐岩缝洞型油藏主要是以构造变形产生的裂缝和岩溶作用形成的孔、缝、洞为主，大裂缝大溶洞发育，具有较强的非均质性和多尺度特征。依据缝洞型碳酸盐岩油藏的开发特点，“缝洞单元”是指周围被相对致密的隔档层体遮挡,由裂缝网络相互串通、由溶孔、溶洞组合而成的多个孤立或孔隙连通的水动力流动单元。每个单元都具有相对独立的压力系统或相对一致的压力变化规律、压力连通关系以及相似的流体性质，在生产中可作为一个相对独立的流体运动单元和油气开采的基本单位。缝洞型油藏开发是以缝洞单元作为基础的，典型缝洞型油藏即典型缝洞单元，是指具有一定规律的缝洞组合、分布模式形成的缝洞单元，如裂缝-溶洞型、地下河-裂缝-地下河型、孤立溶洞-大裂缝型。

典型缝洞油藏的开发指标对于该类储集体的开发具有一定的指导意义[1]。建立一套较为简便的开发指标计算方法对于辅助油田开发、提高采收率研究有重大帮助。

目前缝洞型油藏的地质特征描述已经取得了重大成果[2]。黄朝琴和Arbogast等[3-5]人利用离散缝洞网络模型建立了典型缝洞模型渗透率张量公式，为缝洞型油藏数值模拟提供了基础。姚军等[6]人提出了缝洞型油藏试井解释方法，对于缝洞型油藏的地层压力预测提供了一种较好的方法。康志江等[7]人对于缝洞型油藏渗流特征进行了研究，认为大缝大洞中的流动属于Stokes流动。然而对于碳酸盐岩缝洞型油藏的开发指标，目前尚缺乏一种有效的计算方法，而且渗透率张量公式较为复杂，求解困难。本文对渗透率张量公式进行了简化处理，建立了等效渗透率公式，在保证一定精度的基础上降低了其复杂程度，减少了计算量；并利用等效渗透率公式和Buckley-Leverett理论推导出了典型缝洞油藏的关键开发指标计算方法。

1 等效渗透率

1.1 理论公式建立

针对缝洞型介质等效渗透率，Todd Arbogast等[8]人进行了诸多研究，建立了缝洞型油藏中流体控制方程

(1)

研究表明[8]，对于不同形状介质，渗透率张量表达形式不同，且较复杂缝洞介质其渗透率张量没有理论公式，只能通过数值解法求解。因而对于发育一条层状裂缝的矩形介质，考虑基质的作用，根据式(1)可得其等效渗透率为

(2)

式中：Kfx,Kfy为裂缝在x,y方向的渗透率，μm2；η为交界面处滑移系数；bf为裂缝开度，cm；ly为正方形介质宽度，cm；Km为基质渗透率，μm2。

由式(2)可以看出该理论考虑了基质的作用，同时需要交界面滑移系数等参数，较为复杂。岩心测试表明缝洞型油藏裂缝、溶洞发育，其基质区域的孔隙度和渗透率较小(一般渗透率小于1×10-3μm2，孔隙度小于0.1)。且实验表明基质在束缚水下油相最小启动压力高达20.0 MPa，最小启动压力梯度在10.0 MPa/cm以上，因而流体在基质中的流动能力远远小于在裂缝和溶洞中，相对大溶洞大裂缝来说基质的贡献一般可以忽略不计。因而等效渗透率计算时，只考虑裂缝和溶洞的影响，忽略基质的作用。因此对于发育多条层状裂缝的矩形介质，只考虑裂缝的影响，根据公式(2)可得到裂缝等效渗透率为

(3)

式中：nf为裂缝条数；Af=l·ly为裂缝截面积，cm2。

对于大型溶洞，可以简化为等体积的椭圆管。根据刘新纯[9]的研究，利用泊肃叶公式和牛顿黏滞力定律可以得到倾斜椭圆管状溶洞的泊肃叶定律为

(4)

式中：Qv为沿椭圆管轴线方向流量，cm3/s；a、b为溶洞截面长短轴半长度，cm；pin,pout为进出口压力，MPa；hin,hout为进出口高度，cm；L为椭圆管长度，cm。

结合流量等效原理，可得到溶洞轴向等效渗透率为

(5)

1.2 数值模拟验证

利用COMSOL软件分别对缝长10 cm，缝宽1 cm，不同开度的裂缝和长10 cm，椭圆截面长轴长4 cm，不同短轴长的溶洞中流体单相流进行数值模拟，得到速度剖面分布图(图1、 图2)， 进而计算出等效渗透率，得到等效渗透率曲线(图3、 图4)， 对理论公式(3)、式(5)进行验证。

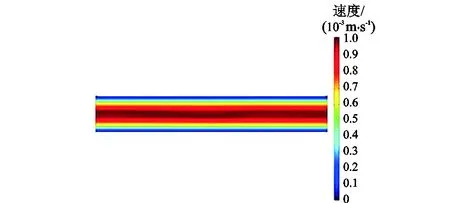
图1 裂缝开度为0.01 cm时裂缝开度方向裂缝中流体速度剖面Fig.1 Velocity profile in crack width direction when crack opening width is 0.01 cm

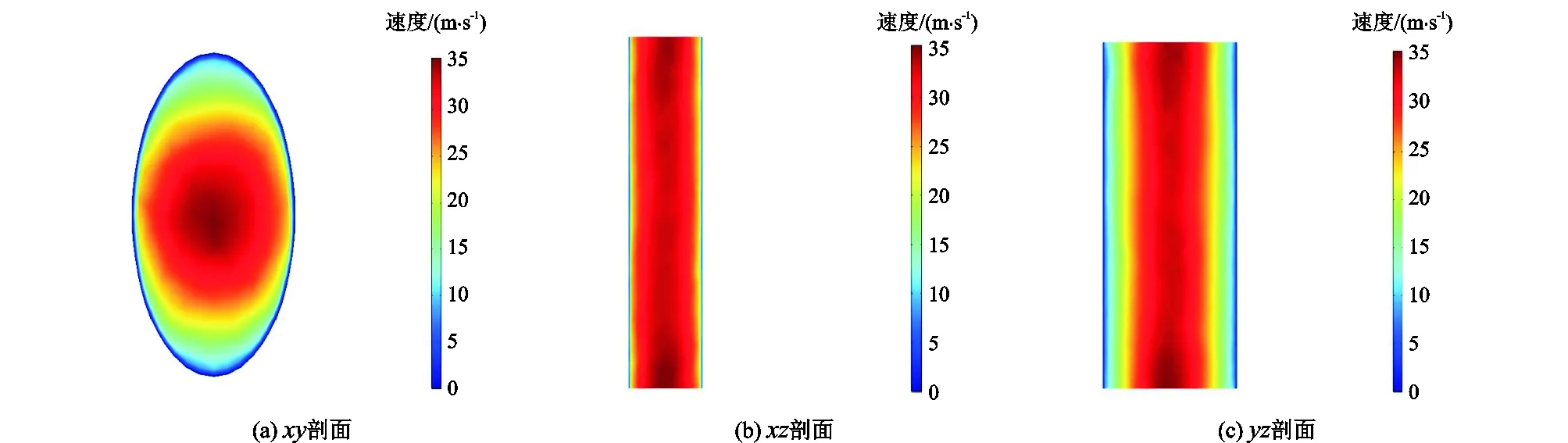
图2 溶洞椭圆截面短轴长2 cm时溶洞中流体速度分布Fig.2 Velocity distribution of fluid in vaggy when short axis of elliptic vuggy is 2 cm

图3 裂缝理论解和数值解对比曲线Fig.3 Comparison of numerical solution with analytical solution of equivalent permeability of crack

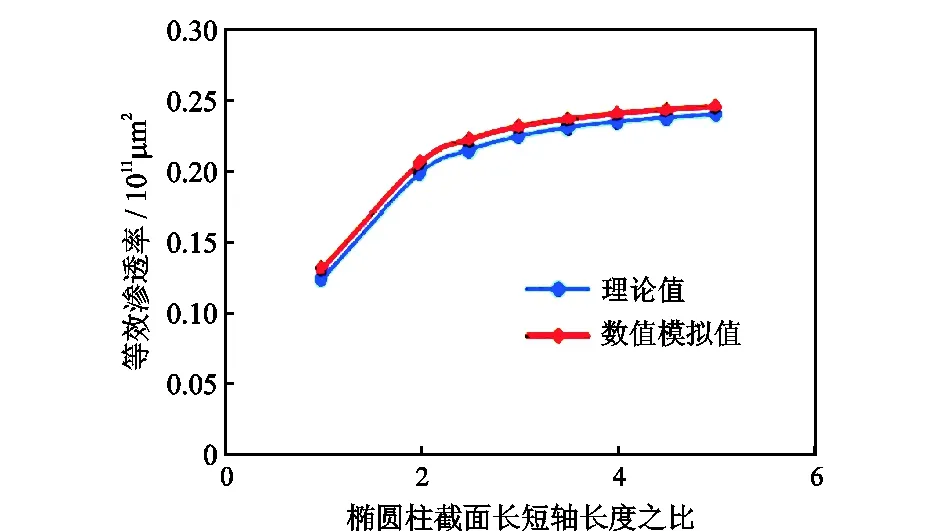
图4 溶洞理论解和数值解对比曲线Fig.4 Comparison of numerical solution with analytical solution of equivalent permeability of elliptic vuggy

从图1裂缝开度方向速度剖面图中可以看出，裂缝中的速度分布呈现抛物线形，符合层状裂缝中的流动特征。由图3可以看出，理论解(式(3))和数值解吻合得较好，但随着裂缝开度和缝长比值得增加，二者的差别会有所增大。这是因为数值解是基于N-S方程进行数值模拟计算得到的，考虑了壁面的黏滞力影响，其结果更加符合地层的实际情况；裂缝开度越大，速度边界层发展越充分，黏滞力影响越明显，因而理论解会偏离数值解。但对于雷诺数远大于1的流体流动来说，其黏滞项相对于速度项可以忽略不计，且野外露头和岩心测试表明，对于大部分裂缝，其开度和长度的比值一般小于0.01，因此用式(3)计算出的渗透率值精确度较高，误差也在可接受范围内(相对误差<5%)。

从图2速度分布图中可以看出，在椭圆管中的各剖面速度分布均符合泊肃叶定律，中间速度大，越靠近壁面速度越小，壁面处速度为零。由图4可知，理论解(式(5))和数值解之间吻合得很好。随着溶洞截面长轴和短轴长度比值的增加，二者之间差距越来越小。由于泊肃叶定律忽略了惯性力的影响，因而式(5)计算出的值偏小。但对于实际溶洞中的流体流动来说，其加速度较小，流体一般处于稳定流状态，流体惯性力可以忽略不计，因此式(5)计算出的渗透率值具有较高的精确度，误差很小。

综上，等效渗透率理论公式和数值模拟结果吻合得较好，可以利用式(3)和式(5)根据流量等效原理组合来计算缝洞系统的等效渗透率K。若裂缝和溶洞倾斜于流动方向时，可以将其分解为垂直于流动方向和平行于流动方向两部分，分别计算；若裂缝、溶洞同时存在时，可利用等值渗流阻力法来计算。

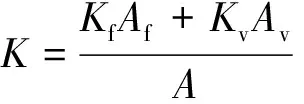
(6)

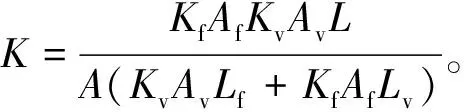
(7)

式中：K为沿流动方向等效渗透率，μm2；Av为溶洞截面积，cm2；A为等效截面积，cm2；L、Lf、Lv分别表示总长度、裂缝长度、溶洞长度，cm。

2 开发指标计算

2.1 基本假设

假设典型缝洞油藏等效渗透率为K；在油水两相流区中，油水同时流动，且都服从广义达西定律；流体不可压缩；考虑重力作用。

此外，大量实验研究证明，缝洞型油藏的相渗曲线属于水相上凸，油相下凹型[10]。由图5可以看出，在不同水相锥进指数下，含水率曲线不再是典型的S型曲线，而表现出Γ型曲线的形状；含水上升率曲线单调递减，没有经典曲线中拐点的存在。这些特点可以表明，缝洞型油藏水驱过程属于渐变式非活塞水驱，见水前没有明显的台阶式水驱前缘，水驱前缘饱和度为残余油饱和度Sw=Swc=0.2。也就是说典型缝洞油藏具有Γ型含水率曲线、渐变式非活塞水驱等特点，其水驱过程含水饱和度分布曲线如图6所示。

图5 不同水相锥进指数时含水率及含水上升率曲线Fig.5 Water-cut and water-cut rising rate curves under different water coning indexes

图6 含水饱和度分布图Fig.6 Distribution curves of water saturation

2.2 理论公式推导

根据上文可知，缝洞型油藏相渗曲线表现出如图7的水相上凸，油相下凹特征。

利用MATLAB CFTOOL工具箱对图7曲线进行拟合得到相渗曲线方程为

图7 典型缝洞模型相渗曲线Fig.7 Relative permeability curve of typical fracture-vuggy model

Krw=a1eb1Sw-c1e-d1Sw,Kro=a2e-b2Sw-c2e-d2Sw。

(8)

式中：Krw,Kro为水相、油相相对渗透率；Sw为含水饱和度；a1、b1、c1、d1、a2、b2、c2、d2为拟合系数，仅与模型缝洞结构组成有关，可由实验获得。

缝洞系统的纵向跨度一般较大[11]，重力作用不能忽略，忽略毛管力考虑重力的含水率[1]为

(9)

考虑重力的油水两相流微分方程为[12]

(10)

上述方程特征线为dSw=0线，即等饱和度线。则式(10)特征方程为

(11)

根据B-L理论，解上述特征方程可得到等饱和度面推进方程为

(12)

对式(12)积分可得水驱前缘(含水饱和度Sw=Swc处)位置为

(13)

2.2.1 见水前开发指标计算

设注水速度为Qi，则有：

(1)瞬时产油量、瞬时产水量

由注采平衡可得

Qo=Qi，Qw=0。

(14)

(2)累积产油量

Np=Qit。

(15)

(3)见水时间

由前文可知，井排见水的判断依据是Sw2>Swf=Swc，水驱前缘含水上升率fw′(Swf)=fw′(Swc)，则有

(16)

2.2.2 见水后开发指标计算

由式(16)可得到见水后时间和含水饱和度关系式为

(17)

结合相渗曲线方程(8)可以得到见水后不同时刻的井排处含水饱和度Sw2，然后根据体积平均法可得到油藏平均含水饱和度为

(18)

(1)瞬时产水量

由含水率定义可得到瞬时产水量为

Qw=Qi·[1-fwg(Sw2)]。

(19)

(2)瞬时产油量

Qo=Qi·fwg(Sw2)。

(20)

(3)累计产油量

由油藏平均含水饱和度可得到

Np=ALφ×{Sw2-Swc-

(21)

(4)累积产水量

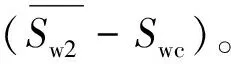
(22)

(5)采收率

(23)

2.3 数值模拟验证

利用数值模拟软件COMSOL对水驱油过程进行模拟，对开发指标计算公式(18)、式(19)、式(23)进行验证。

应用COMSOL软件中的CFD模块对缝洞中的流体流动进行数值模拟计算。流体在较大裂缝和溶洞中的流动满足N-S方程，属于Navier-Stokes流动。COMSOL软件利用相场法(Phase Field)对缝洞系统中的两相流进行求解。计算所用几何模型由2组相交裂缝和2组椭圆柱状溶洞交替排列而成，如图8所示。几何模型参数为：缝长3.54 m，缝开度0.1 m，缝宽0.8 m，倾斜角度45°；溶洞长2.5 m，椭圆截面长轴长2 m，短轴长1 m。边界条件为：注入端，定流量Qi=0.1 m3/s；采出端，定压力，p=0 MPa。根据式(6)、式(7)可计算出其等效渗透率为K=5×106μm2。

图8 典型缝洞几何模型Fig.8 Schematic diagram of typical fracture-vuggy geometry model

流体基本参数为：水相黏度μw=1.2 mPa·s，油相黏度μo=5 mPa·s。

2.4 结果分析

利用COMSOL软件对实际模型进行水驱油模拟，得到产油量、产水量及采收率曲线，与理论公式得到的结果进行对比，结果如图9—图11所示。

由图9—图11中曲线可以看出，理论曲线和两种数值模拟曲线吻合得较好。瞬时产油量随时间增加而下降，且下降趋势越来越慢，这是由于随着油藏开采，含油饱和度降低，油相相对渗透率下降，导致瞬时产油量减少；同时随着含水饱和度的增加，油相相对渗透率下降速率减小，从而瞬时产油量下降趋势减缓。

瞬时产水量趋势与此相反，随时间增加而增加，最终达到一个较为稳定的状态，这是由于缝洞型油藏水相相渗曲线表现为上凸型，随着开采得进行，含水饱和度增加，但水相相对渗透率增加速率越来越慢，导致产水速度随时间增加而减缓。

采收率随时间增加而增加，最终达到一个较高的平稳水平。由于模型复杂程度不高，且没有考虑溶洞充填情况，水驱过程进行得较为彻底，因而采收率相对较高。

图9 瞬时产油量曲线Fig.9 Instantaneous oil production curves of typical fracture-vuggy model

图10 瞬时产水量曲线Fig.10 Instantaneous water production curves of typical fracture-vuggy model

图11 采收率曲线Fig.11 Recovery factor curves of typical fracture-vuggy model

2.5 不同典型缝洞组合模式下理论和数值模拟结果对比

设计了两种不同典型缝洞组合模式(图12、图13)，分别利用理论公式和COMSOL数值模拟软件对水驱油过程进行计算模拟，得到瞬时产油量曲线如图14、图15所示。

图12所示模型为缝-洞结构与孤立溶洞通过一条大裂缝相连接；图13所示模型为缝-洞结构与竖井-地下河结构通过地下河相连接。

从图14、图15中可以看出对于不同缝洞组合模式，理论曲线和数值模拟曲线吻合得很好，这表明开发指标理论计算公式具有较高准确度。

图12 孤立溶洞-大裂缝型和正交裂缝-溶洞型组合模式几何模型Fig.12 Schematic diagram of isolated vug-large crack and orthogonal fractures-vug combination model

图13 地下河-竖井型和正交裂缝-溶洞型组合模式几何模型Fig.13 Schematic diagram of underground river-vertical vug and orthogonal fractures-vug combination model

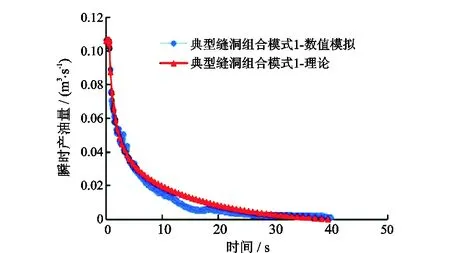
图14 孤立溶洞-大裂缝型和正交裂缝-溶洞型组合模式下瞬时产油量曲线Fig.14 Instantaneous oil production curves of isolated vug-large crack and orthogonal fractures-vug combination model

图15 地下河-竖井型和正交裂缝-溶洞型组合模式下瞬时产油量曲线Fig.15 Instantaneous oil production curves of underground river-vertical vug and orthogonal fractures-vug combination model

3 结 论

(1)对渗透率张量公式进行了简化处理，在计算时忽略了基质的影响，只考虑了裂缝和溶洞的渗透率，建立了等效渗透率公式，既保证了一定的精度，又减少了计算量。

(2)综合运用Buckley-Leverett理论、等效渗透率理论对典型缝洞油藏模型的开发指标进行推导计算，得到了瞬时产油量、瞬时产水量、采收率等开发指标理论公式，并与数值模拟结果做了对比，所得结果与数值模拟结果吻合较好。

(3)随着开采进行，含油饱和度降低，油相相对渗透率减小，瞬时产油量随时间增加而减少，但下降速度逐渐减小；瞬时产水量随时间增加而增加，由于水相相渗曲线为上凸型，导致其增加速度逐渐减缓，最终达到较平稳的水平；由于模型水驱过程进行的较为彻底，采收率较高。

(4)对于实际油藏中多种缝洞组合模式，提出的开发指标理论计算公式具有较高准确度，可以应用于不同缝洞组合模式下的开发指标计算。

[1] 姜汉桥.油藏工程原理与方法[M].北京:石油大学出版社,2003.

JIANG Hanqiao.Principles and Methods ofReser-voir Engineering[M].Beijing:China University of Petroleum Press,2003.

[2] 龚洪林,袁刚,田彦灿,等.塔中碳酸盐岩缝洞型储集体精细成像[J].地球物理学进展,2012,27 (2):555-561.

GONG Honglin,YUAN Gang,TIAN Yancan,et al.Accurate imaging way of carbonate fracture cave type’s reservoir in Tazhong[J].Progress in Geophysics,2012,27(2):555-561.

[3] 黄朝琴,姚军,李亚军,等.基于均匀化理论的缝洞型介质渗透性分析[J].中国科学(技术科学),2010,40(9):1095-1103.

HUANG Zhaoqin,YAO Jun,LI Yajun,et al.Permeability analysis of fractured vuggy porous media based on homogenization theory[J].Science China (Technological Sciences),2010,40(9):1095-1103.

[4] ARBOGAST T,BRUNSON D S.A computational method for approximating a Darcy-Stokes system governing a vuggy porous medium[J].Computational Geosciences,2007,11(3):207-218.

[5] 杨坚.缝洞型碳酸盐岩油藏缝洞单元数值模拟理论与方法研究[D].东营:中国石油大学,2007.

YANG Jian.Study of numerical simulation theory and method of fractured-vug unit in fractured vuggy carbonate reservoirs[D].Dongyiing:China Univer-sity of Petroleum,2007.

[6] 姚军,王子胜.缝洞型碳酸盐岩油藏试井解释理论与方法[M].东营:中国石油大学出版社,2007.

YAO Jun,WANG Zisheng.Theory and Method for Well Test Interpretation in Fractured-vuggy Carbonate Reservoirs[M].Dongying:China University of Petr-oleum Press,2007.

[7] 康志江,李江龙,张冬丽,等.塔河缝洞型碳酸盐岩油藏渗流特征[J].石油与天然气地质,2005,26(5):634-640.

KANG Zhijiang,LI Jianglong,ZHANG Dongli,et al.Percolation characteristics of fractured-vuggy carbonate reservoir in Tahe oilfield[J].Oil and Gas Geology,2005,26(5):634-640.

[8] ARBOGAST T,BRUNSON D S,BRYANT S L,et al.A preliminary computational investigation of a macro model for vuggy porous media[J].Develop-ments in Water Science,2015,55(1):267-278.

[9] 刘新纯.倾斜椭圆柱管中流体的Poiseuille公式[J].数理医药学杂志,2007,20(5):735-736.

LIU Xinchun,The fluid Poiseuille’s formula in Ell-ipse cylindrical of inclination[J].Journal of Mathe-matical Medicine,2007,20(5):735-736.

[10] 李阳.碳酸盐岩缝洞型油藏开发理论与方法[M].北京:中国石化出版社,2014.

LI Yang,Development Theory and Method of Carbo-nate Fractured vuggy Reservoir[M].Beijing:Sinopec press,2014.

[11] 吕爱民.碳酸盐岩缝洞型油藏油藏工程方法研究[D].东营:中国石油大学,2007.

LYU Aimin,Study of reservoir engineering meth-ods for fractured vuggy carbonate reservoirs[D].Dongying:China University of Petroleum,2007.

[12] 张建国,雷光伦,杜殿发,等.油气层渗流力学[M].东营:中国石油大学出版社,2009.

ZHANG Jianguo,LEI Guanglun,DU Dianfa,et al.Oil and Gas Seepage Mechanics[M].Dongying:China University of Petroleum Press,2009.